
Parametrické rovnice přímky v rovině

Přímka určená bodem A=[a_1;a_2] a směrovým vektorem \vec{u}=(u_1;u_2) má parametrické rovnice tvaru:
\begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array}
Zkráceně můžeme vyjádřit p:X=A+t\vec{u}, číslo t nazýváme parametr. Pokud známe dva body A, B ležící na přímce, směrový vektor je například \vec{u}=\overrightarrow{AB}.
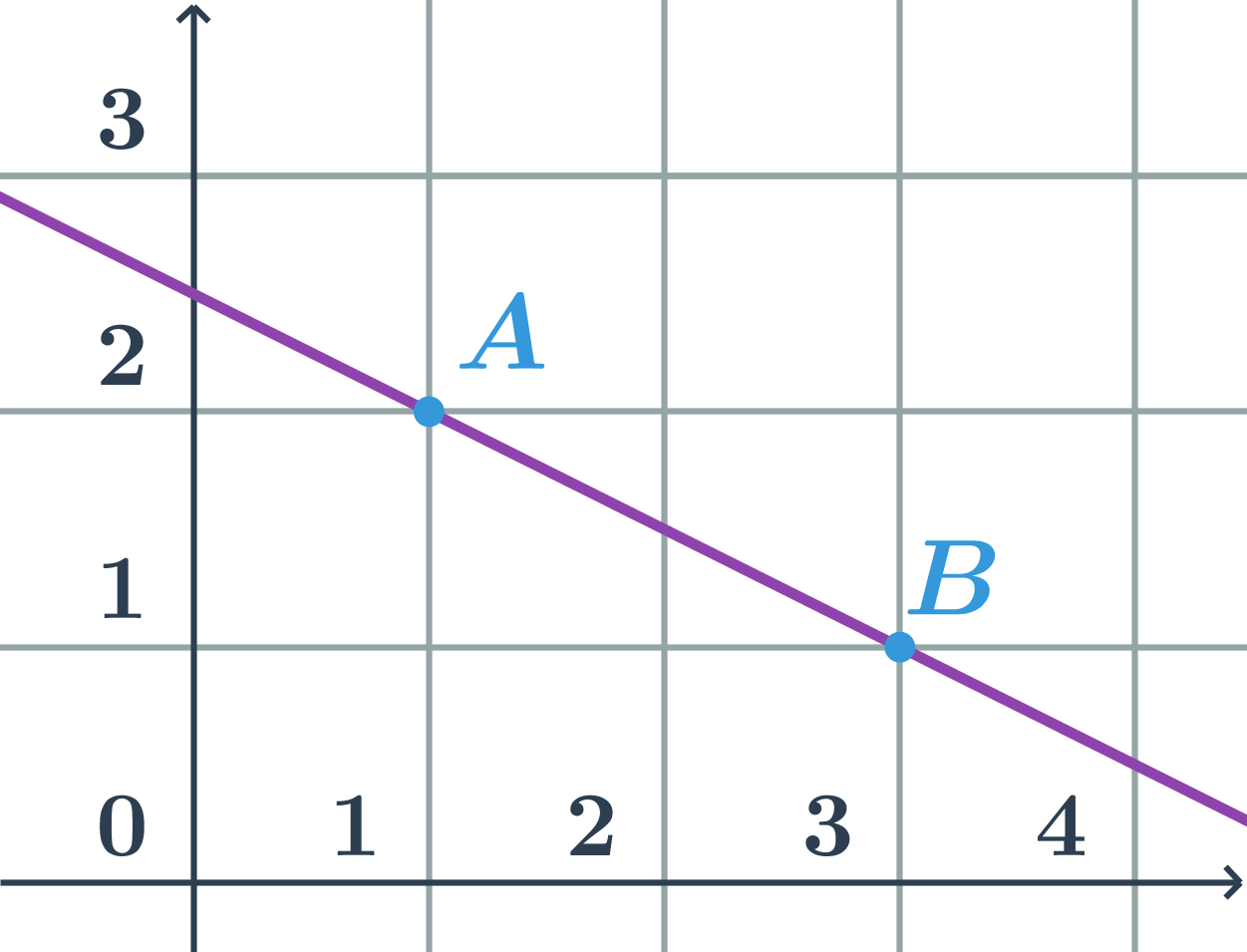
Parametrické rovnice přímky p určené body A=[1;2] a B=[3;1]
- přímka p je určená bodem A a směrovým vektorem \vec{u}=\overrightarrow{AB}=B-A=(2;-1)
- parametrické rovnice přímky p: \begin{array}{rrl}x&=&1+2t\\y&=&2-t\\&&t\in\mathbb{R}\end{array}
Různé parametrické rovnice přímky na obrázku
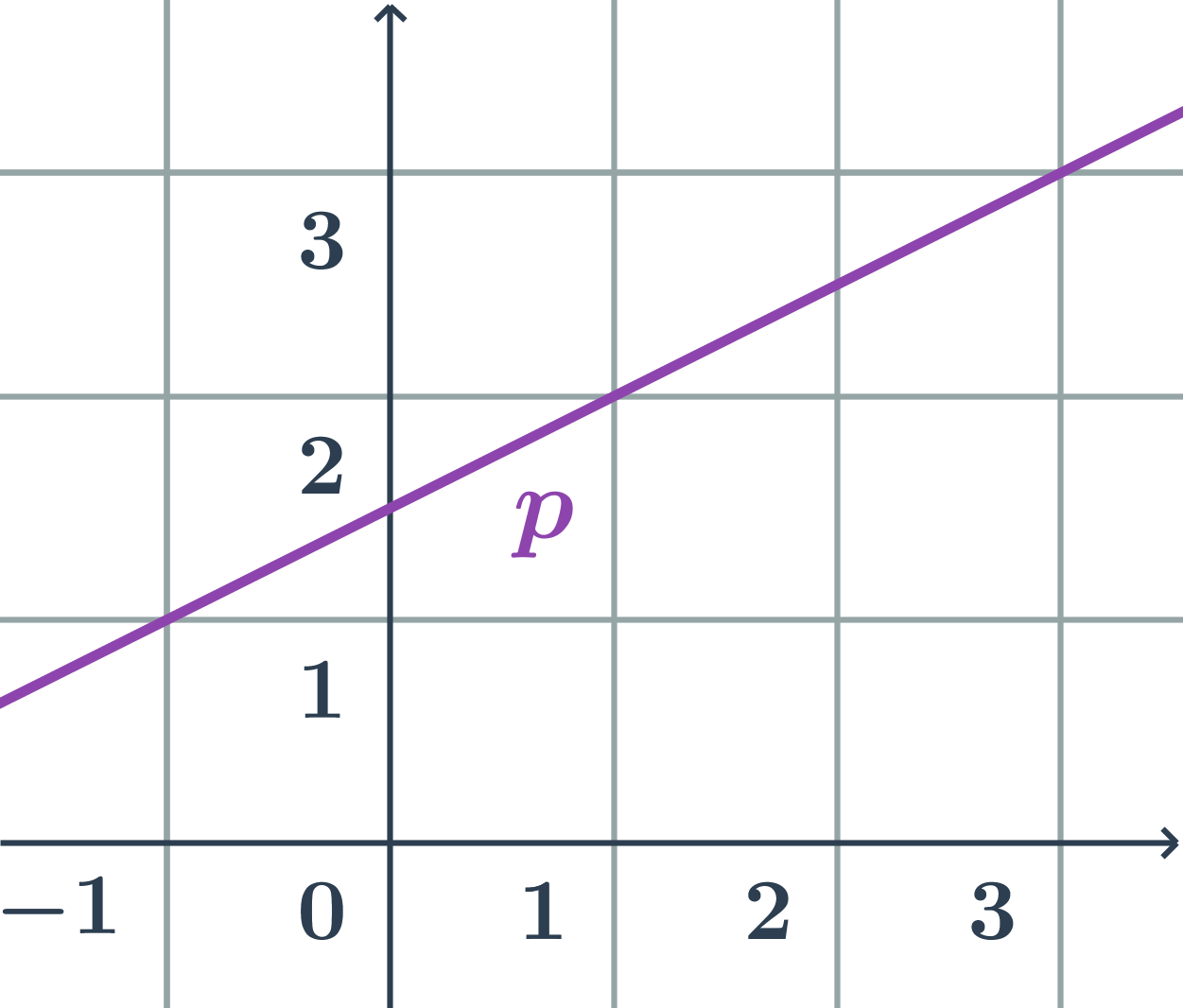
Určíme souřadnice směrového vektoru a jednoho bodu na přímce:
- například: \vec{u}=(2;1), A=[1;2]
- parametrické rovnice přímky p: \begin{array}{rrl}x&=&1+2t\\y&=&2+t\\&&t\in\mathbb{R}\end{array}
Další možnost parametrického vyjádření:
- \vec{v}=(-4;-2), B=[3;3]
- parametrické rovnice přímky p: \begin{array}{rrl}x&=&3-4t\\y&=&3-2t\\&&t\in\mathbb{R}\end{array}
Pro určení parametrických rovnic můžeme vybrat kterýkoliv bod ležící na přímce a jakýkoliv zápis souřadnic směrového vektoru, možností jak parametricky vyjádřit danou přímku je tedy nekonečně mnoho.
Zavřít











