Krychle a kvádr – 1. třída (1. ročník)

Krychle a kvádr jsou oba prostorové geometrické útvary, které patří mezi mnohostěny, speciálněji jde o zvláštní případy hranolů.

Krychle je prostorový útvar, který má šest stěn, tvar každé stěny je čtverec. Všechny hrany krychle mají stejnou délku a všechny vnitřní úhly jsou pravé, tedy jejich velikost je 90°. Příklady krychle v běžném životě zahrnují kostky cukru nebo Rubikovu kostku.

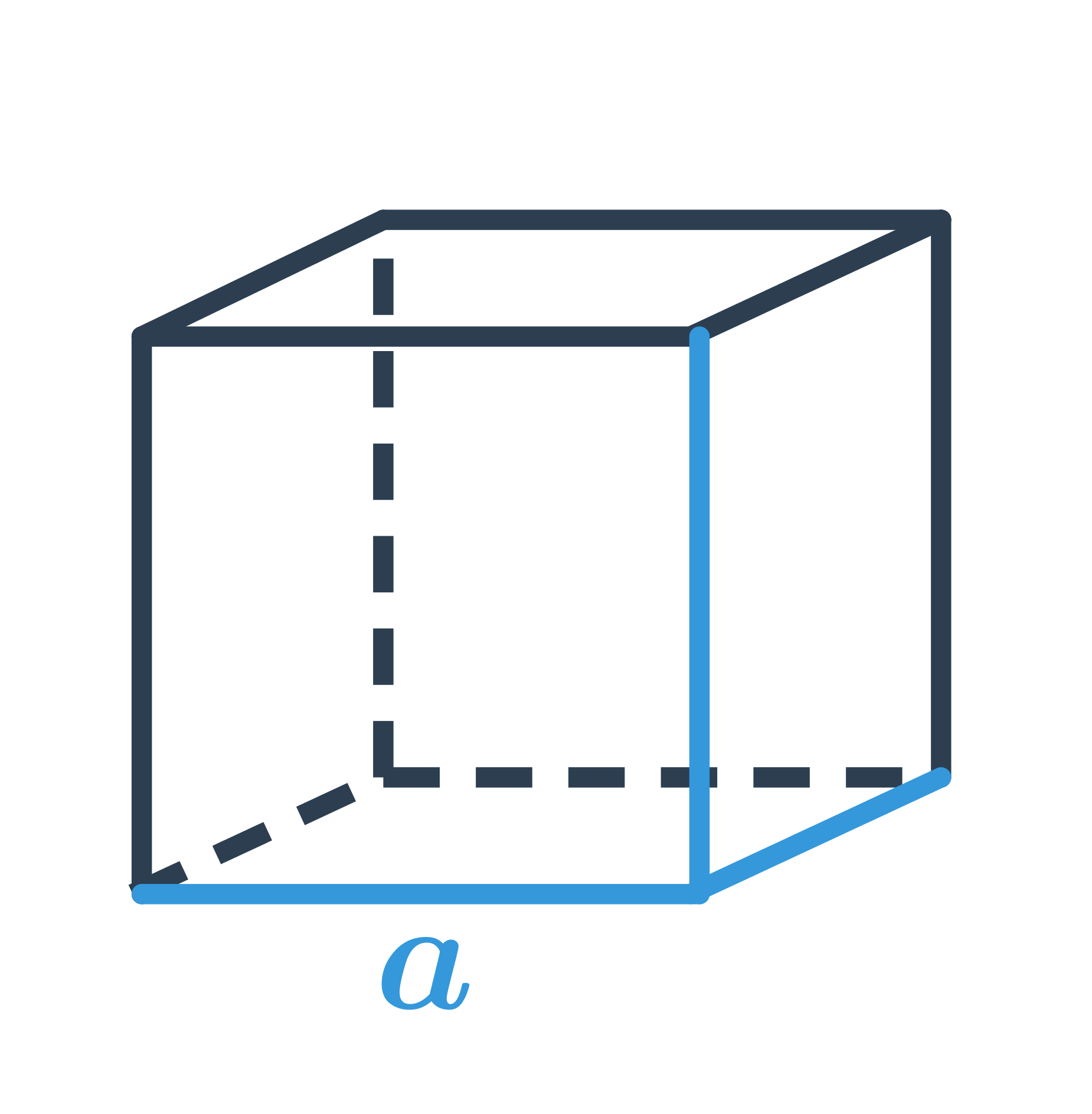
Pro výpočet objemu krychle použijeme vzorec V = a^3, kde a je délka hrany krychle.

Povrch krychle s délkou hrany a se vypočítá pomocí vzorce S = 6a^2.

Kvádr je také hranol, ale na rozdíl od krychle mají jeho stěny tvar obdélníků. Kvádr má tři rozměry: šířku, délku a výšku, které nemusí být stejné, jako je tomu u krychle. Kvádr má šest stěn, tvar každé stěny je obdélník nebo čtverec, pokud jsou všechny stěny tvaru čtverce, jde o krychli.

Příklady kvádrů v běžném životě zahrnují krabice, knihy nebo cihly.

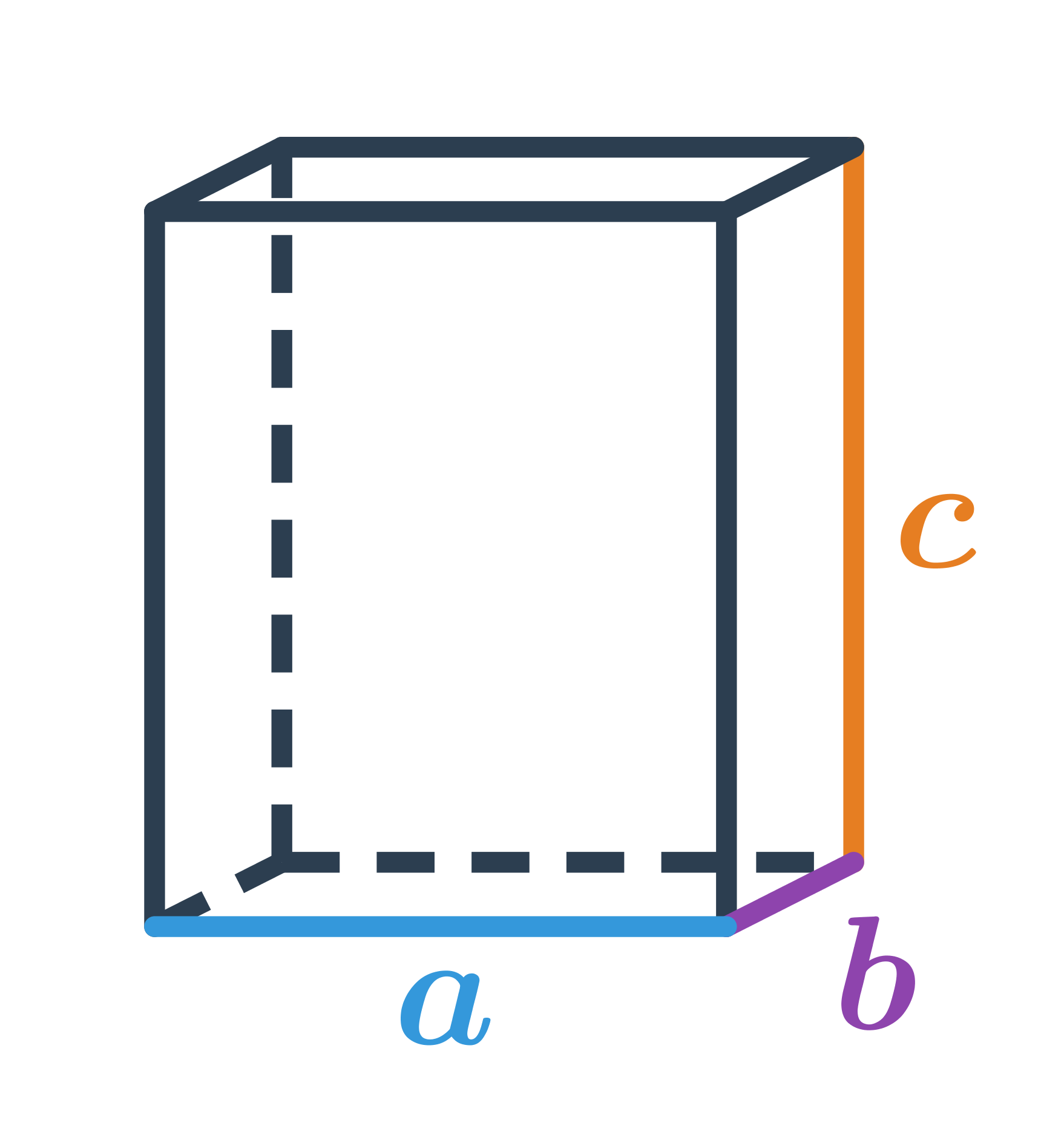
Objem kvádru získáme vzorcem V = a \cdot b \cdot c, kde a,b,c jsou rozměry kvádru.

Povrch kvádru vypočítáme jako součet obsahů všech jeho šesti obdélníkových stěn S = 2(ab + bc + ac). Dvojice protějších stěn jsou shodné obdélníky, proto mají stejné obsahy.