Logaritmická funkce je inverzní k exponenciální funkci o stejném základu. Grafy dvou navzájem inverzních funkcí jsou osově souměrné podle osy prvního kvadrantu (tj. přímky splňující x=y).
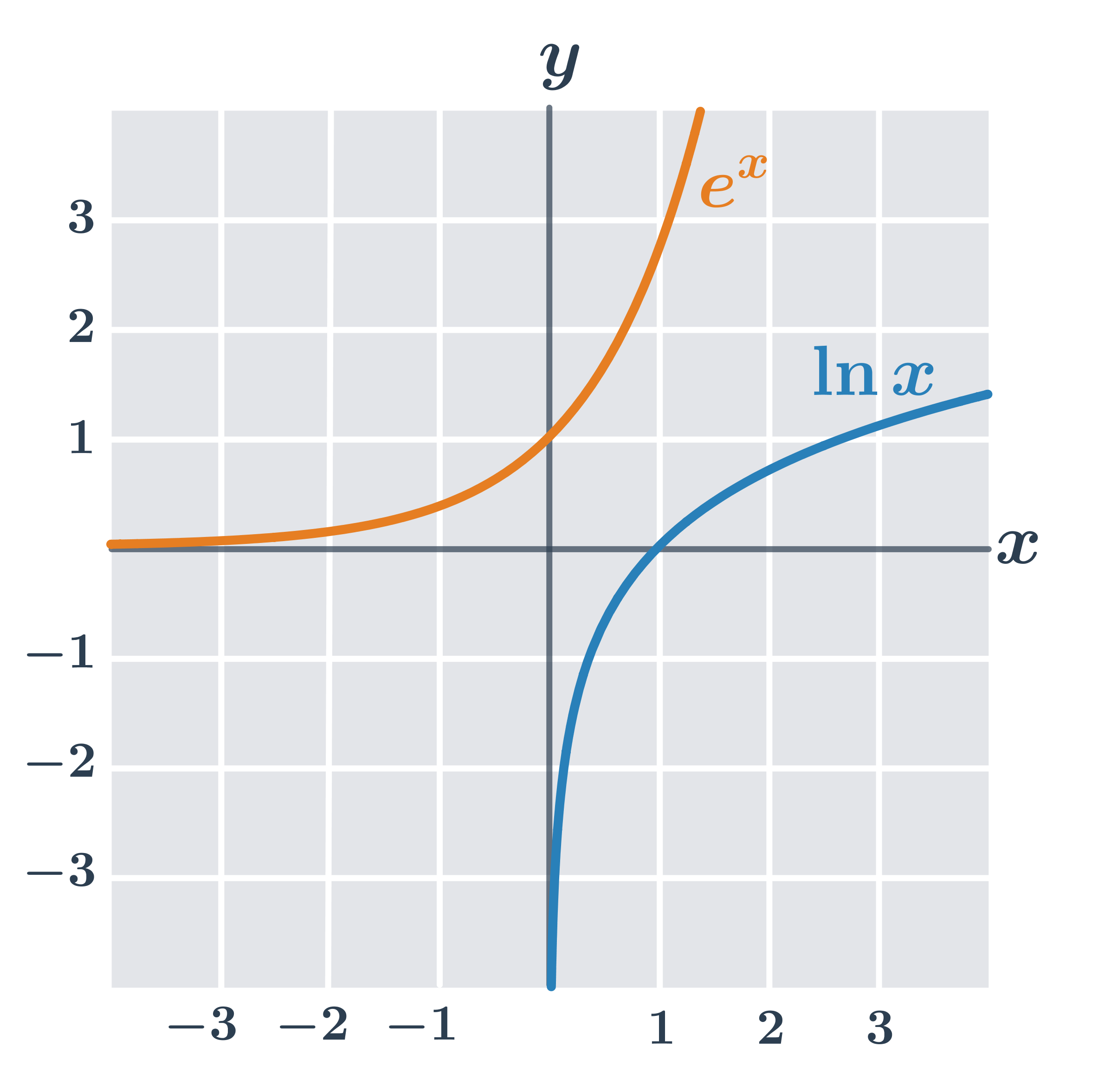
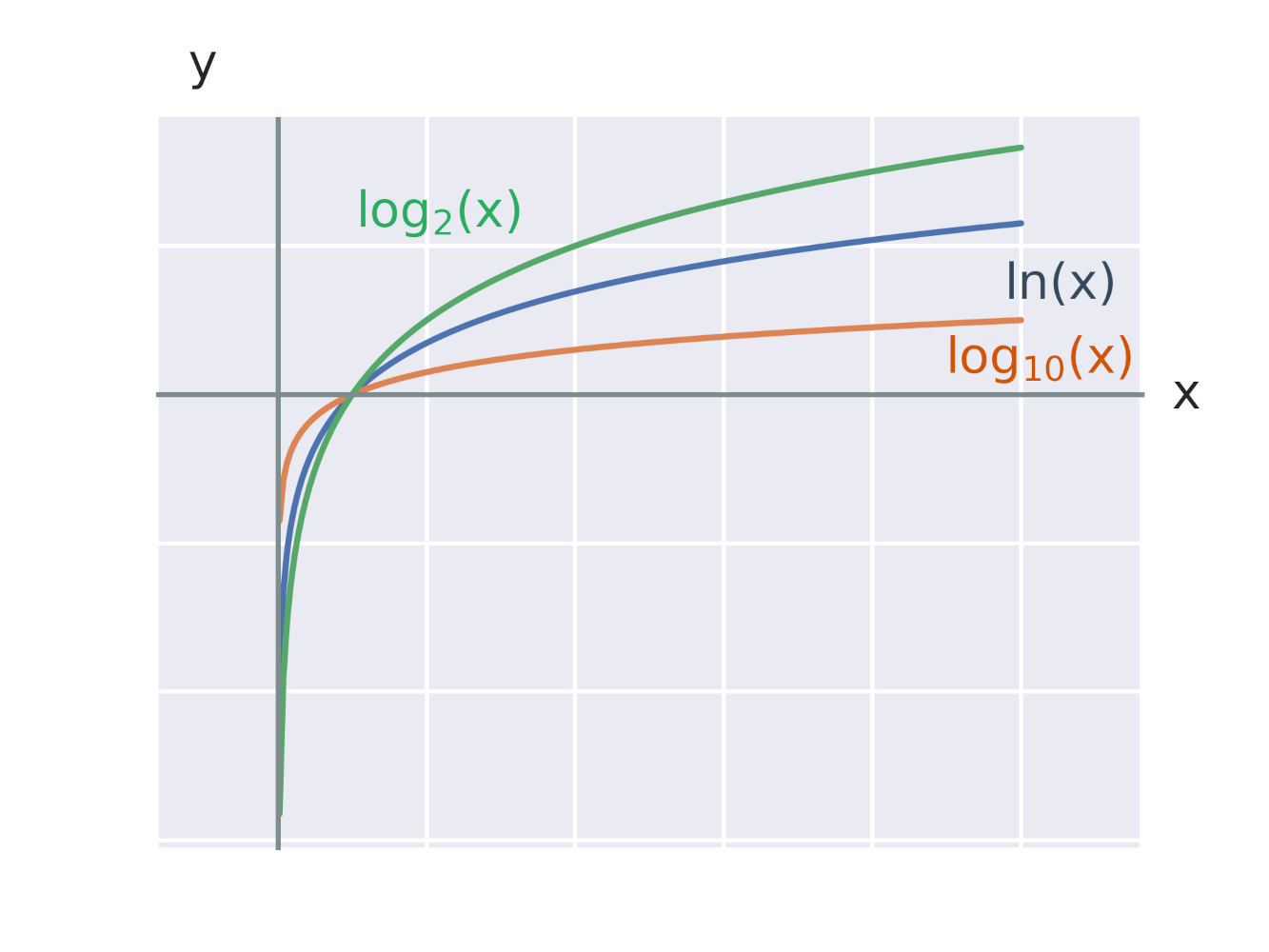
Graf každé logaritmické funkce tvaru y=\log_a x prochází bodem [1,0], protože pro libovolnou konstantu a platí: \log_a 1=0. Na obrázku vidíme grafy logaritmických funkcí s různými základy 2, e, 10.
Značení některých význačných logaritmických funkcí:
| funkce | popis | další možná značení |
|---|---|---|
| \log_a x | obecně logaritmus x o základu a pro nějaké a >0, a\neq 1 | |
| \ln x | přirozený logaritmus x, tj. logaritmus x o základu e | v angl. textech někdy \log x |
| \log x | dekadický logaritmus x, tj. logaritmus x o základu 10 | \log_{10}x |
| \log_2 x | binární logaritmus x, tj. logaritmus x o základu 2 | někdy se objevuje \mathrm{lb}\;x |
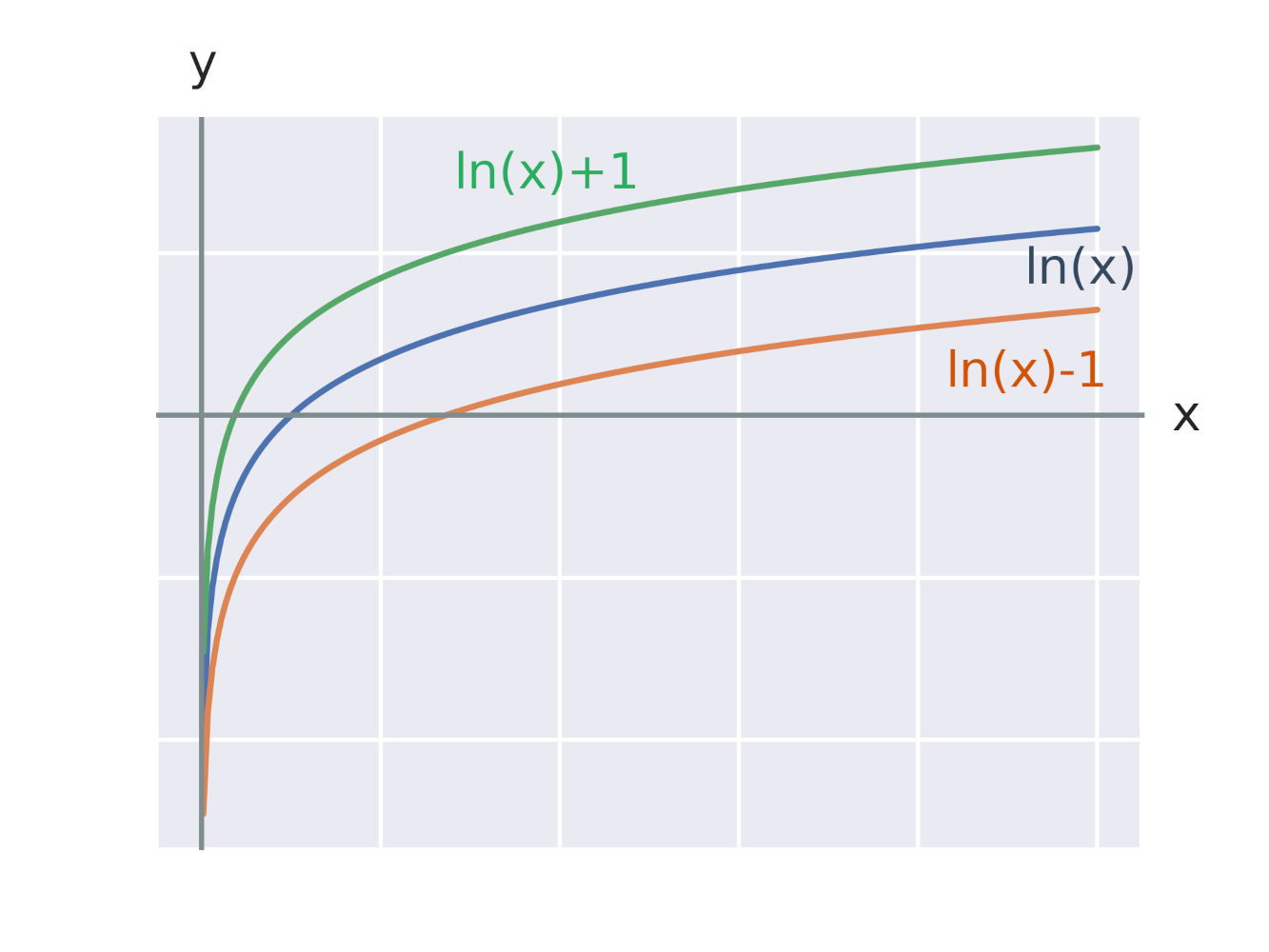
Efekt přičtení konstanty k logaritmické funkci
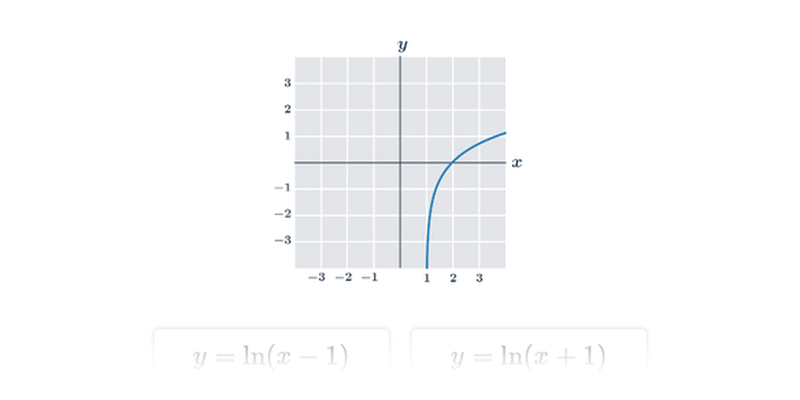
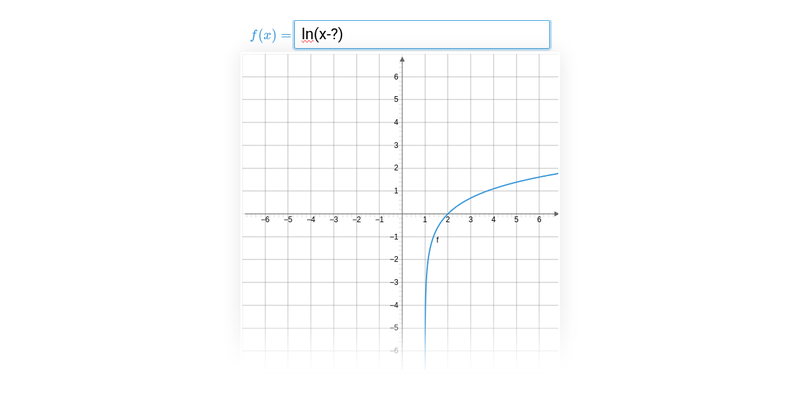
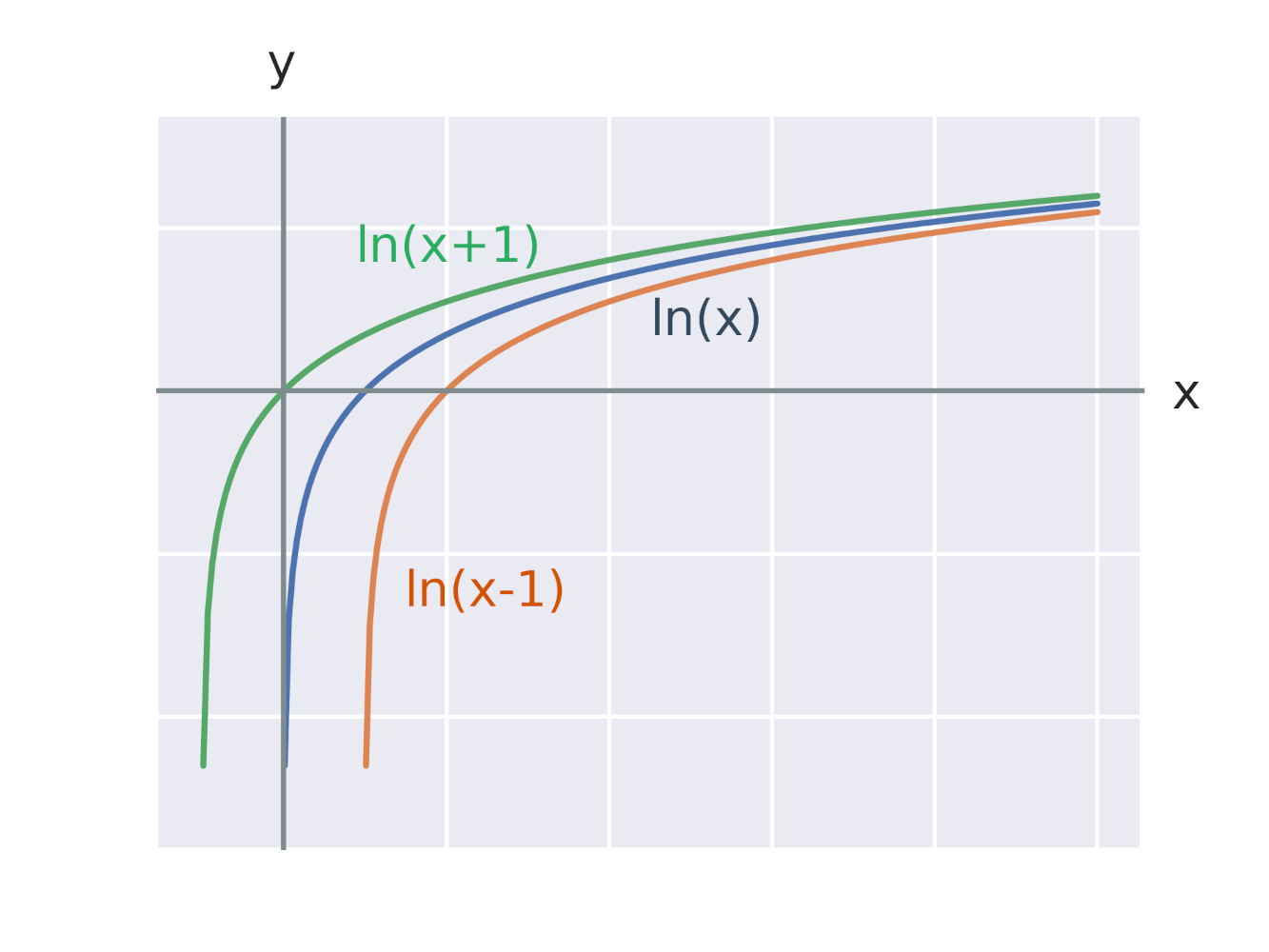
Efekt přičtení konstanty k argumentu logaritmické funkce
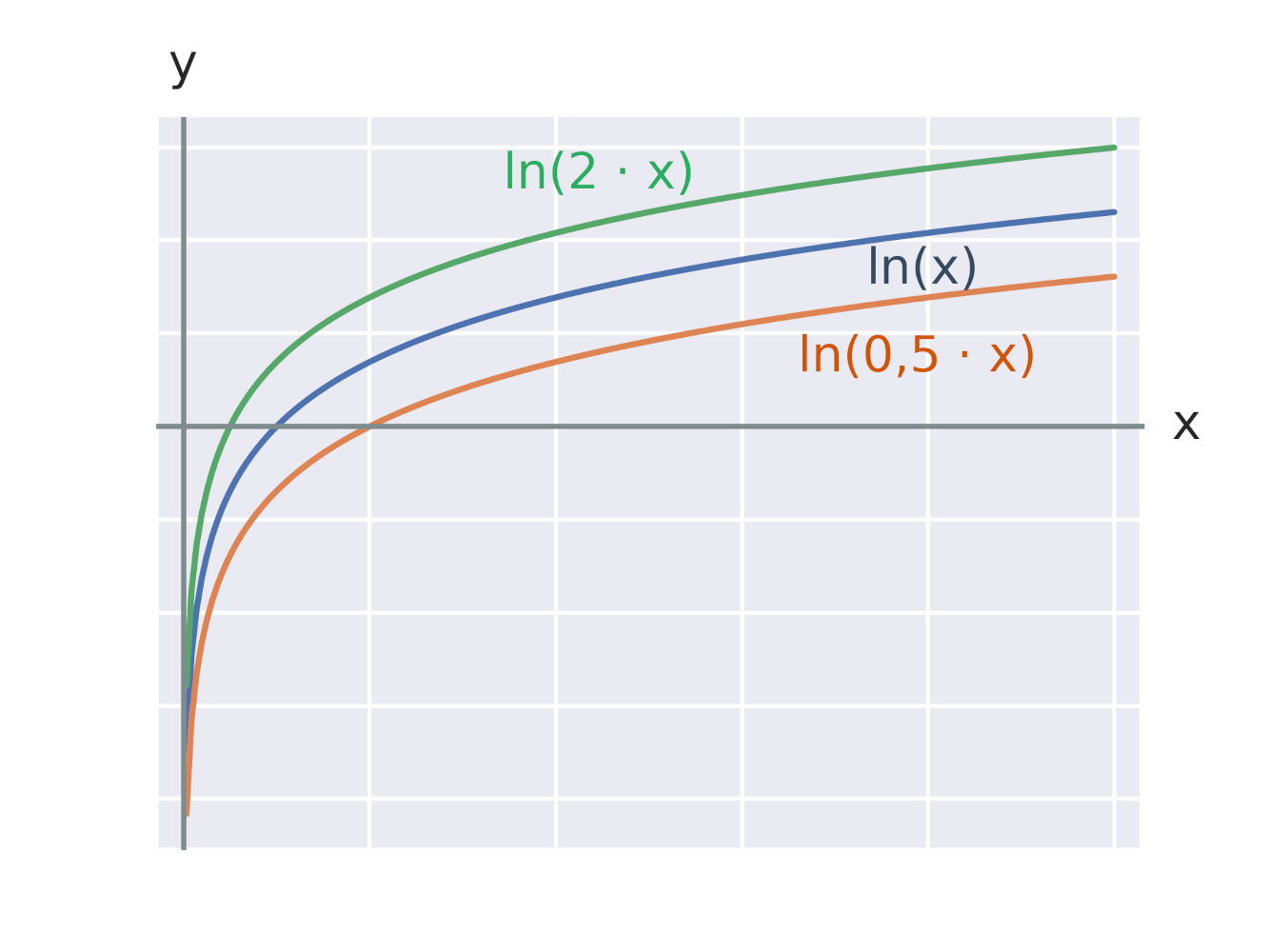
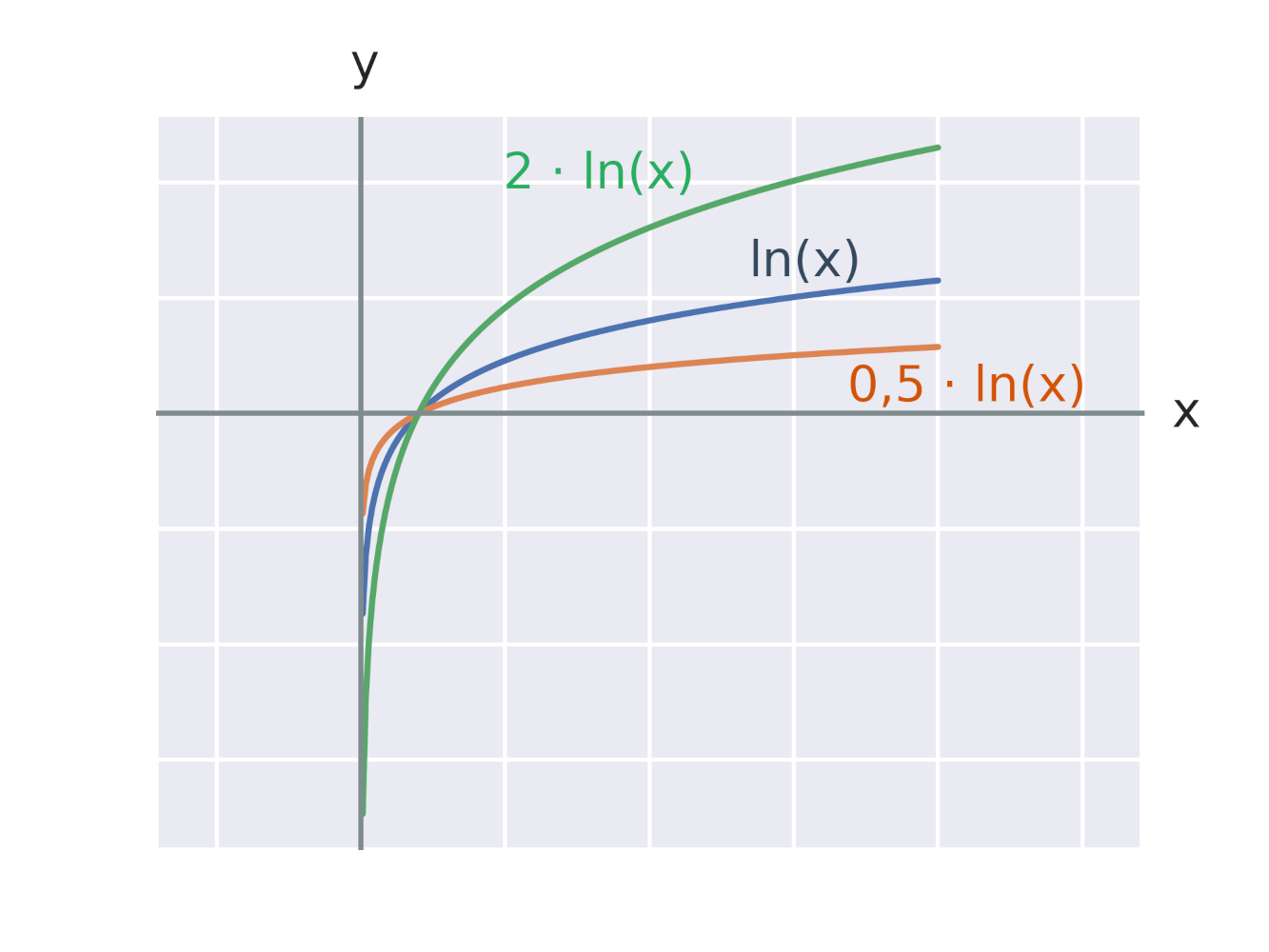
Efekt vynásobení logaritmické funkce konstantou
Efekt vynásobení argumentu logaritmické funkce konstantou