Skvěle, štít %% dosažen
Grafy logaritmických funkcí » Rozhodovačka »
Přejít na téma:
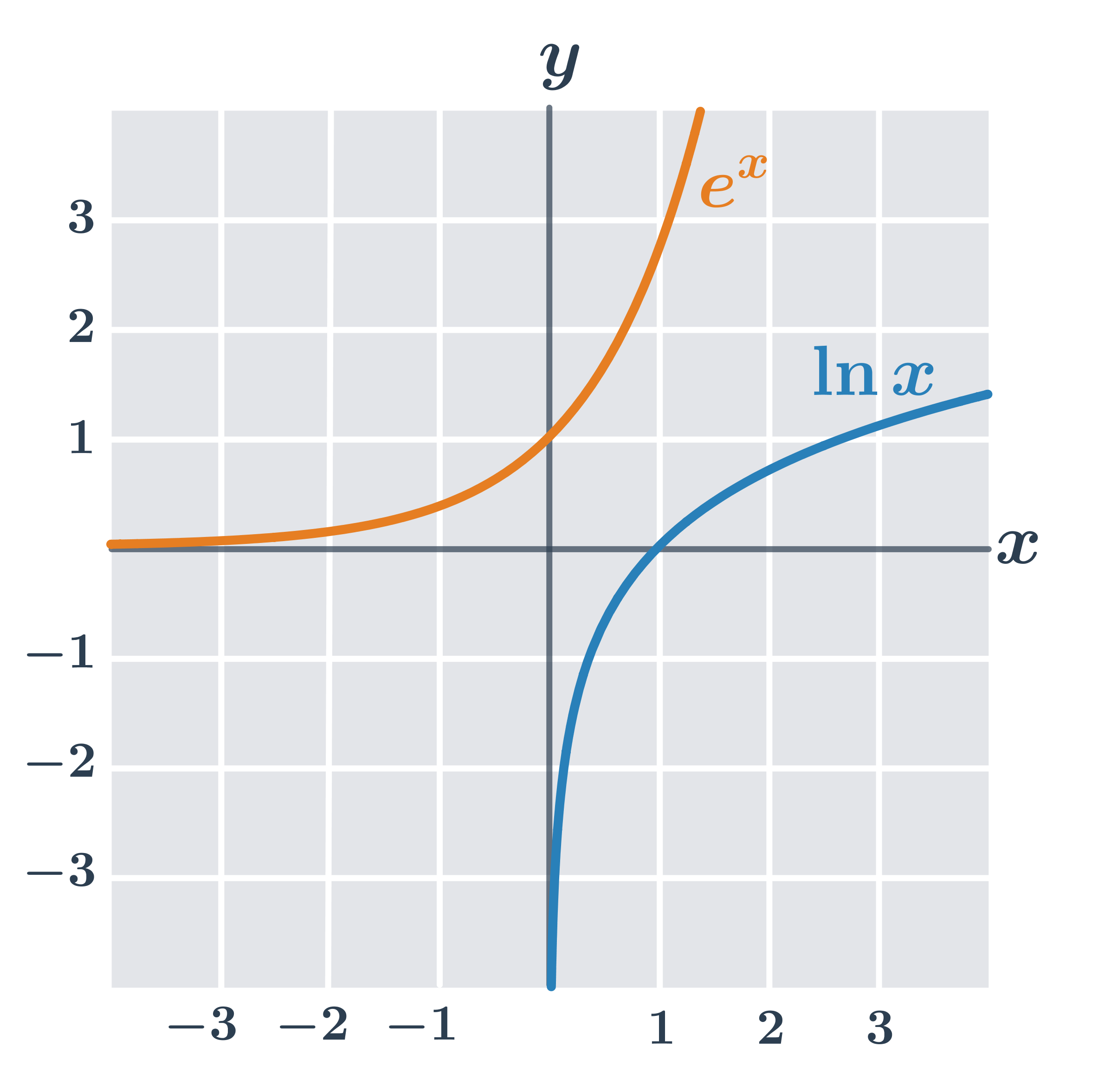
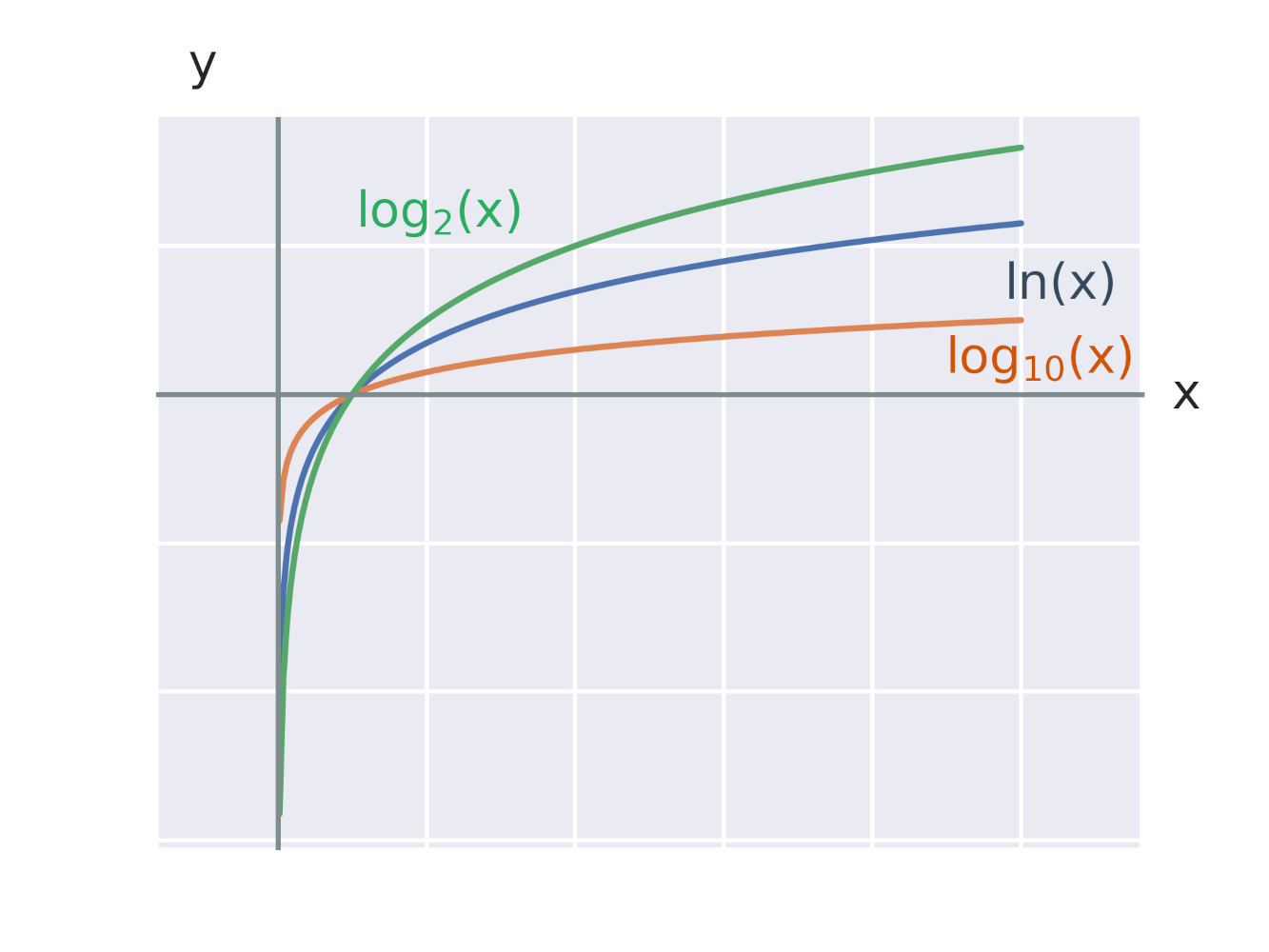
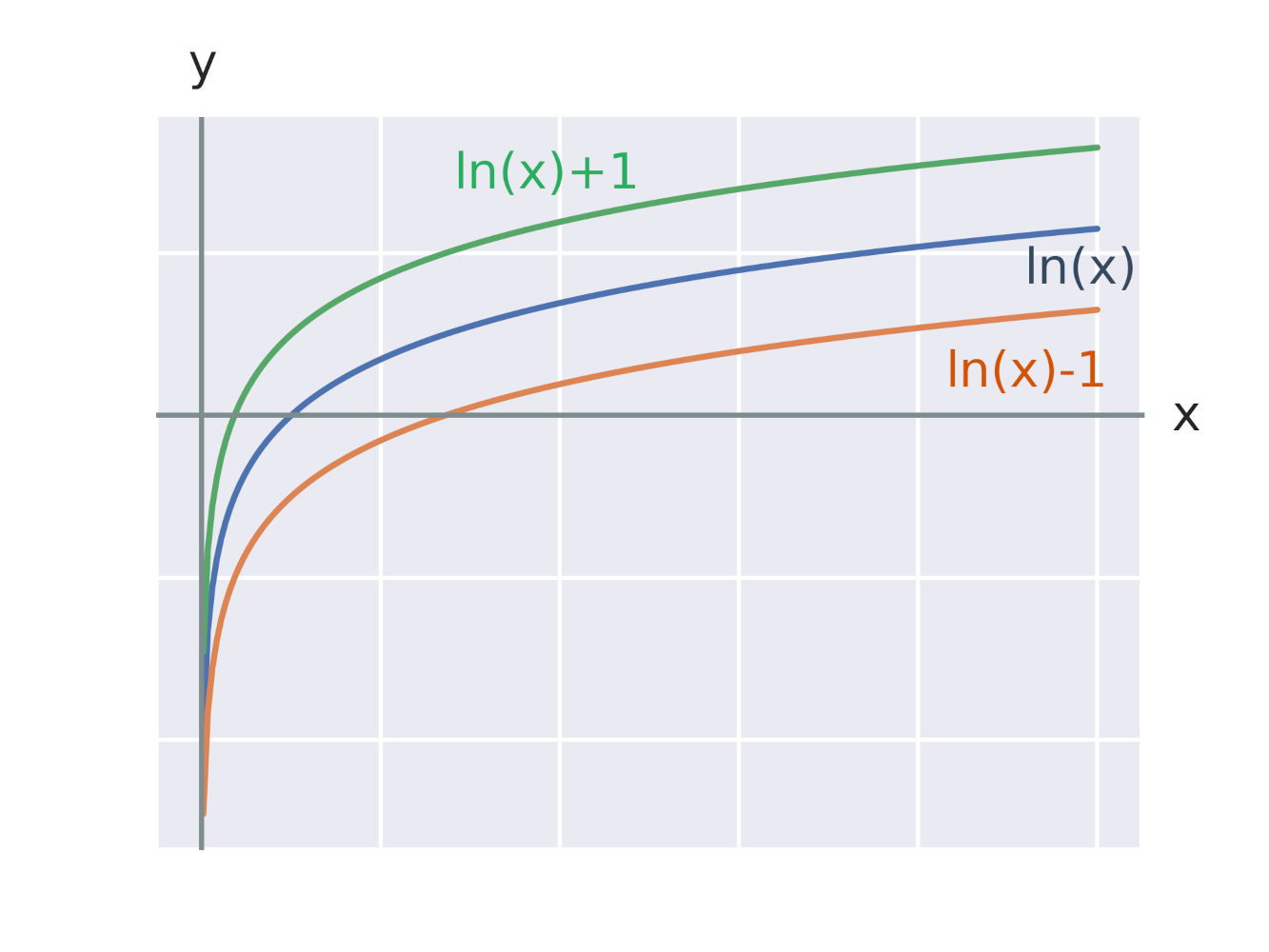
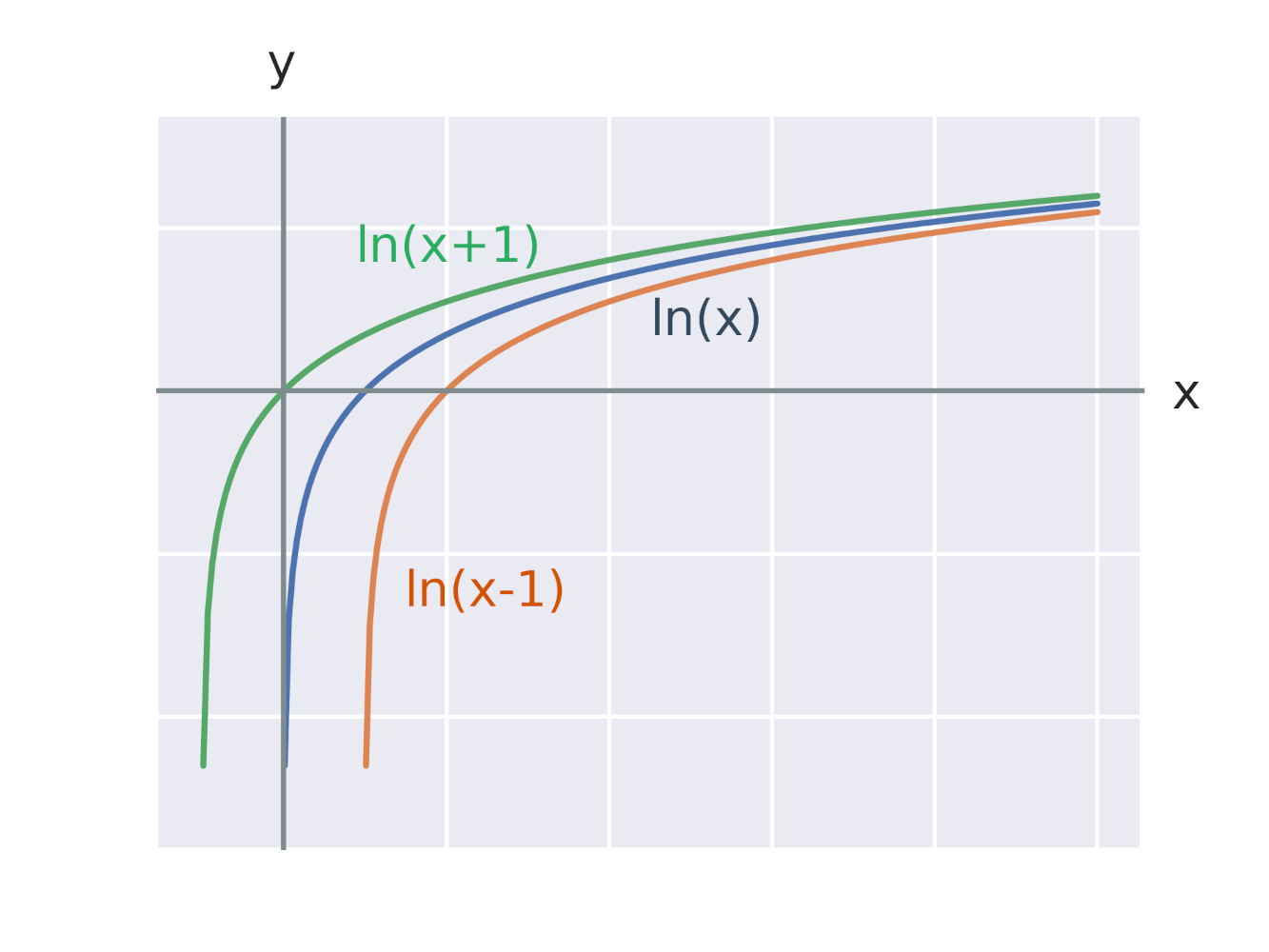
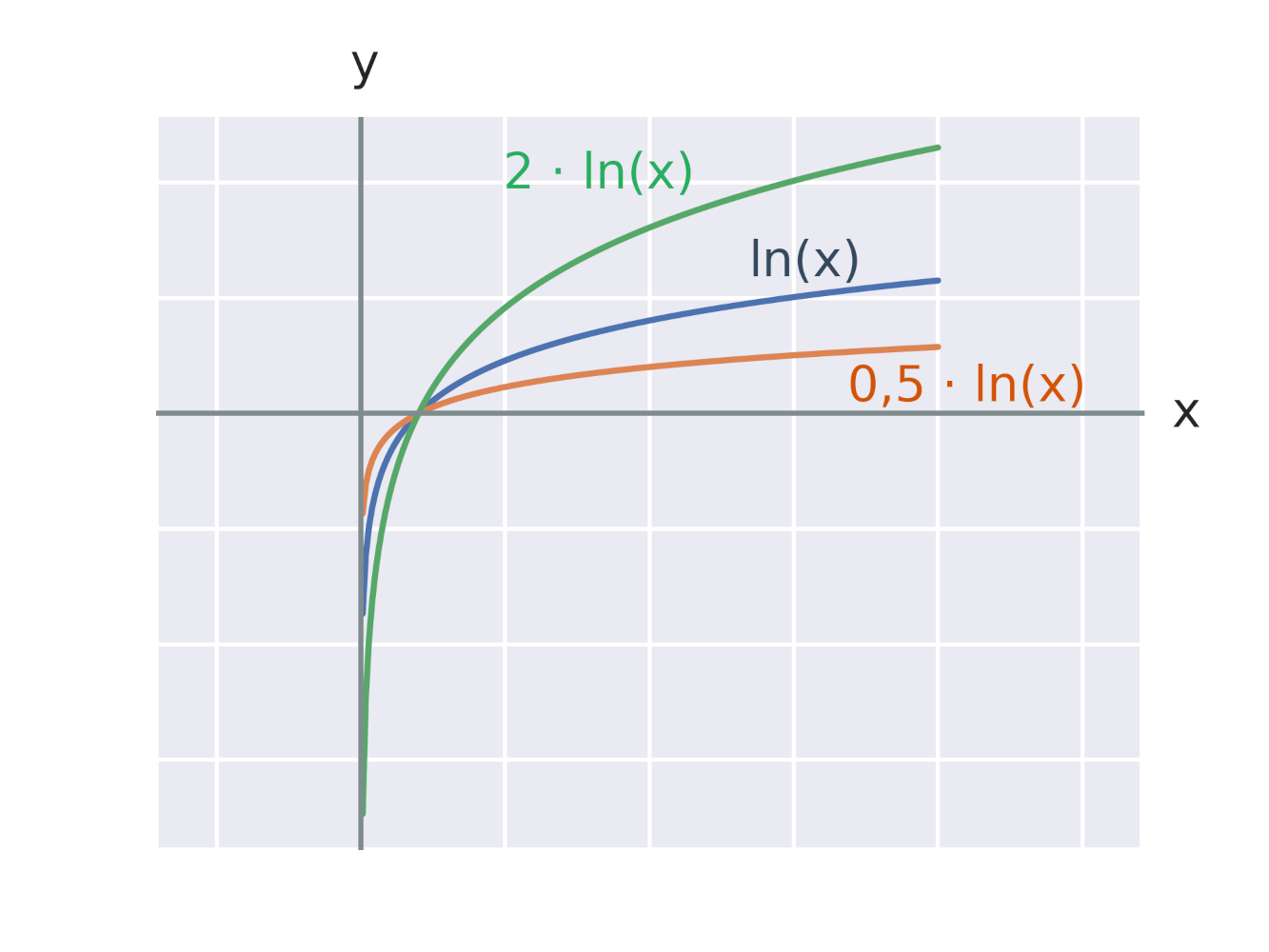
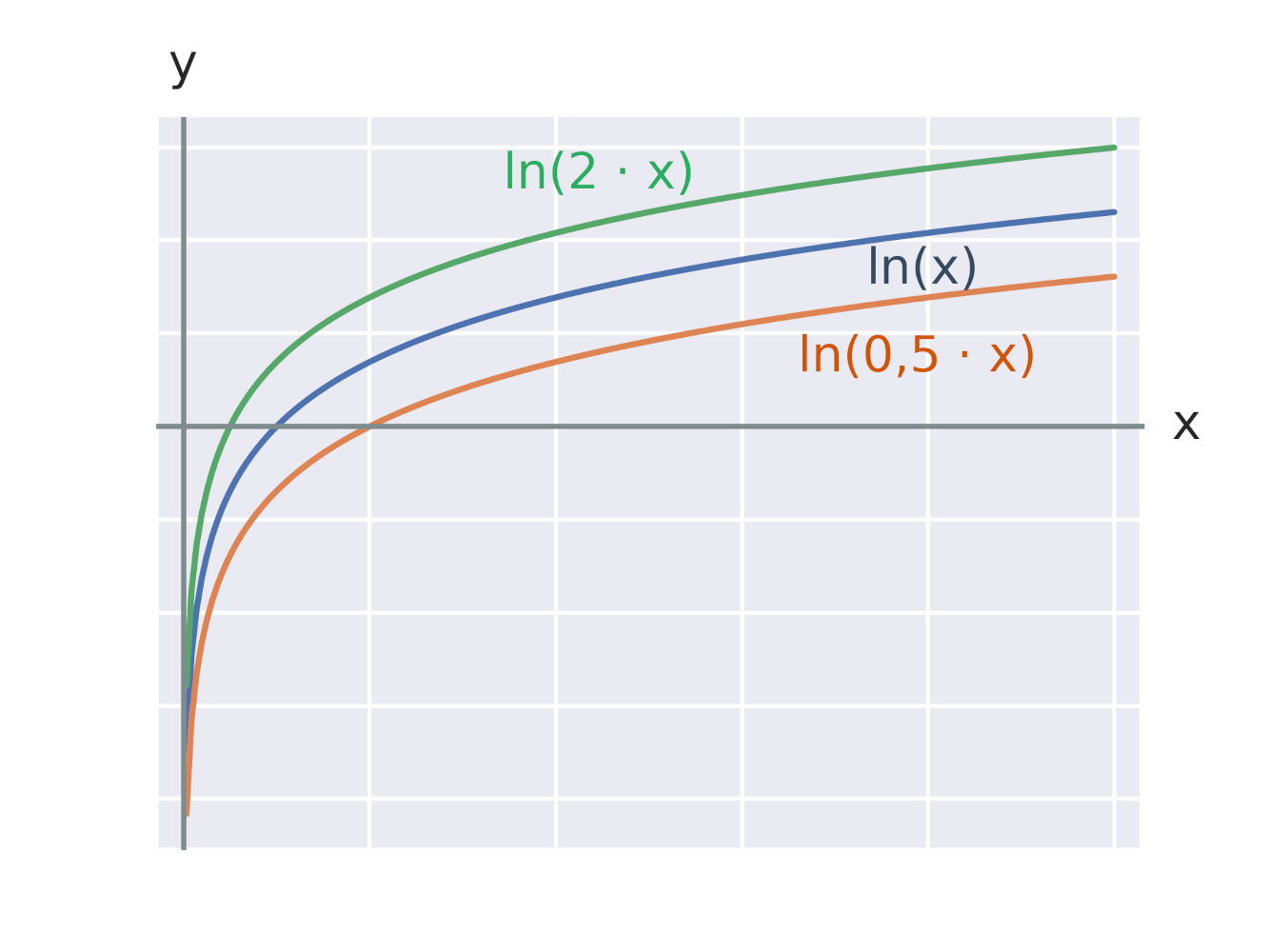
Grafy logaritmických funkcí
Grafy logaritmických funkcí
Přejít na cvičení:
Rozhodovačka
Rozhodovačka
Zobrazit na celou obrazovku
Zobrazit shrnutí tématu
Sdílet
Zobrazit nastavení cvičení
QR kód
QR kód lze naskenovat např. mobilním telefonem a tak se dostat přímo k danému cvičení nebo sadě příkladů.
Kód / krátká adresa
Tříznakový kód lze napsat do vyhledávacího řádku, také je součástí zkrácené adresy.
Zkopírujte kliknutím.
G1X
umime.to/G1X
Nastavení cvičení
Pozor, nastavení je platné pouze pro toto cvičení a předmět.
Grafy logaritmických funkcí (těžké)