Výpis souhrnů

Stejnolehlost

Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.

« Zpět na procvičování

Podtémata

Stejnolehlost

Stejnolehlost

Přejít ke cvičením na toto téma »

Stejnolehlost je daná bodem S a nenulovým číslem \lambda. Bod S se nazývá střed stejnolehlosti, číslo \lambda je koeficient stejnolehlosti.

Obrazem bodu X je bod X', pro který platí:

|SX'|=|\lambda| \cdot |SX|
pro \lambda \gt 0 leží X, X' na stejné polopřímce s počátkem S
pro \lambda \gt 0 leží X, X' na opačných polopřímkách s počátkem S

Na obrázku je vidět, kde leží obraz X' bodu X v závislosti na hodnotě koeficientu \lambda:

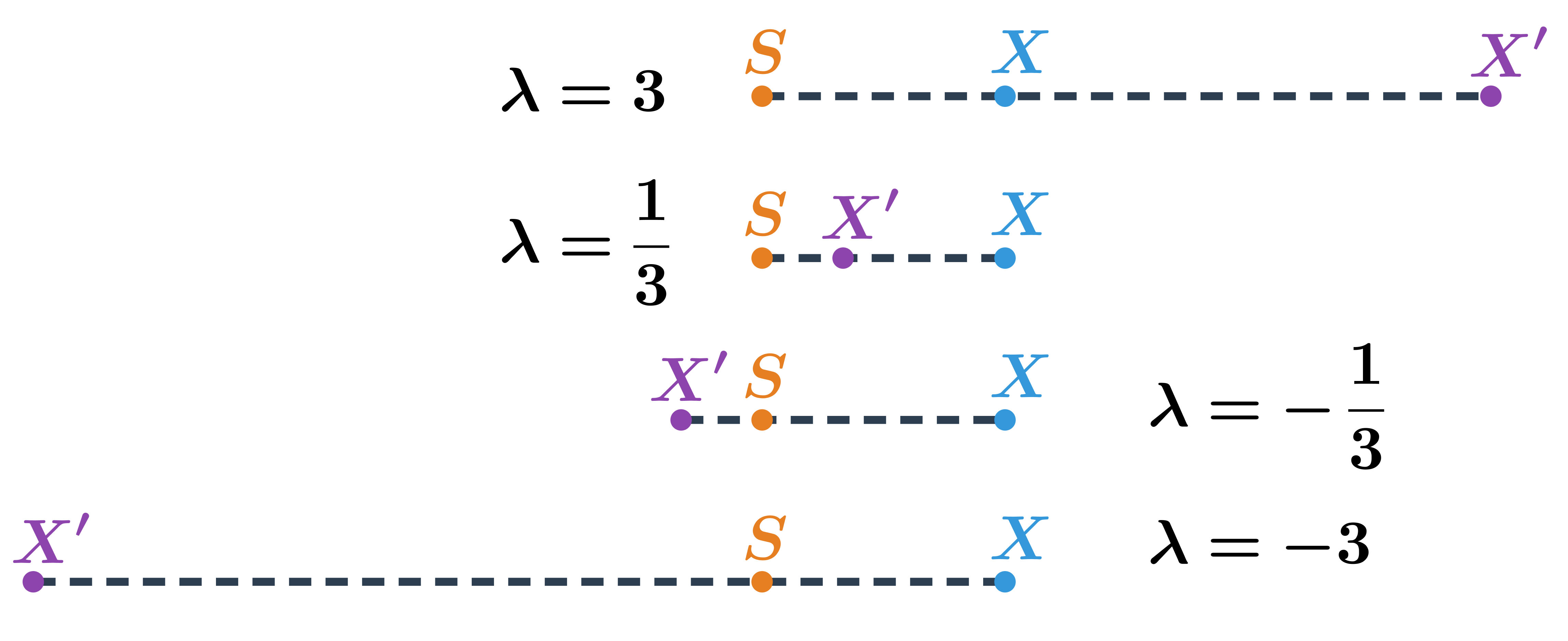
Přehled vlastností obrazu X' bodu X ve stejnolehlosti se středem S pro různé hodnoty koeficientu \lambda:

\lambda \gt 0	bod X' leží na polopřímce SX
\lambda \lt 0	bod X' leží na polopřímce opačné k SX
\|\lambda\| \gt 1	bod X' má od středu S větší vzdálenost než bod X
\|\lambda\| \lt 1	bod X' má od středu S menší vzdálenost než bod X

Příklad 1: obraz trojúhelníku ve stejnolehlosti

Obraz trojúhelníku ABC ve stejnolehlosti se středem S a koeficientem \lambda =\frac{1}{2}

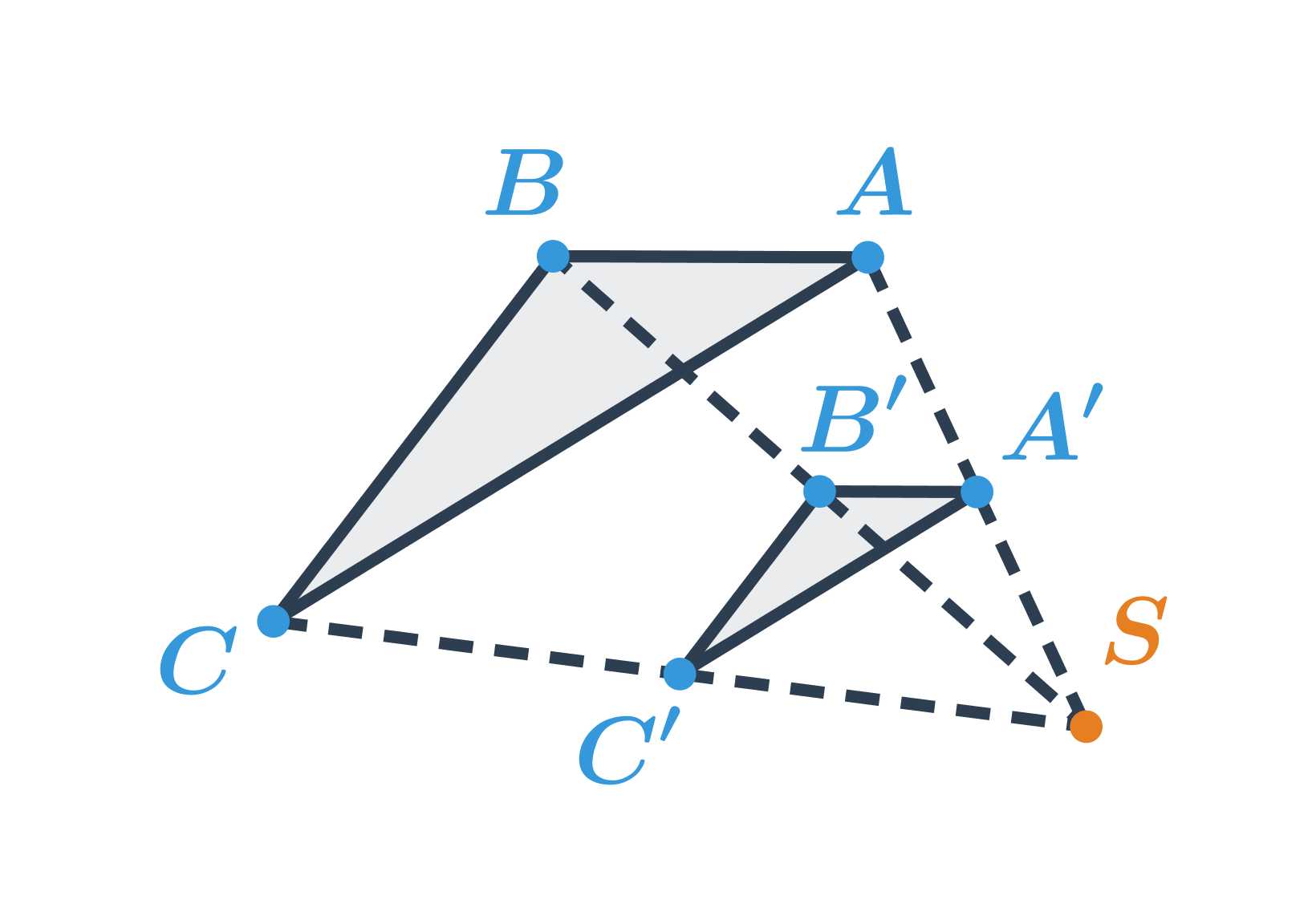
Pro délky odpovídajících si úseček platí: \frac{|SA'|} {|SA|}=\frac{|SB'|} {|SB|}=\frac{|SC'|} {|SC|}=\frac{1}{2}

Příklad 2: obraz kružnice ve stejnolehlosti

Obraz kružnice k ve stejnolehlosti se středem S a koeficientem \lambda =-3.

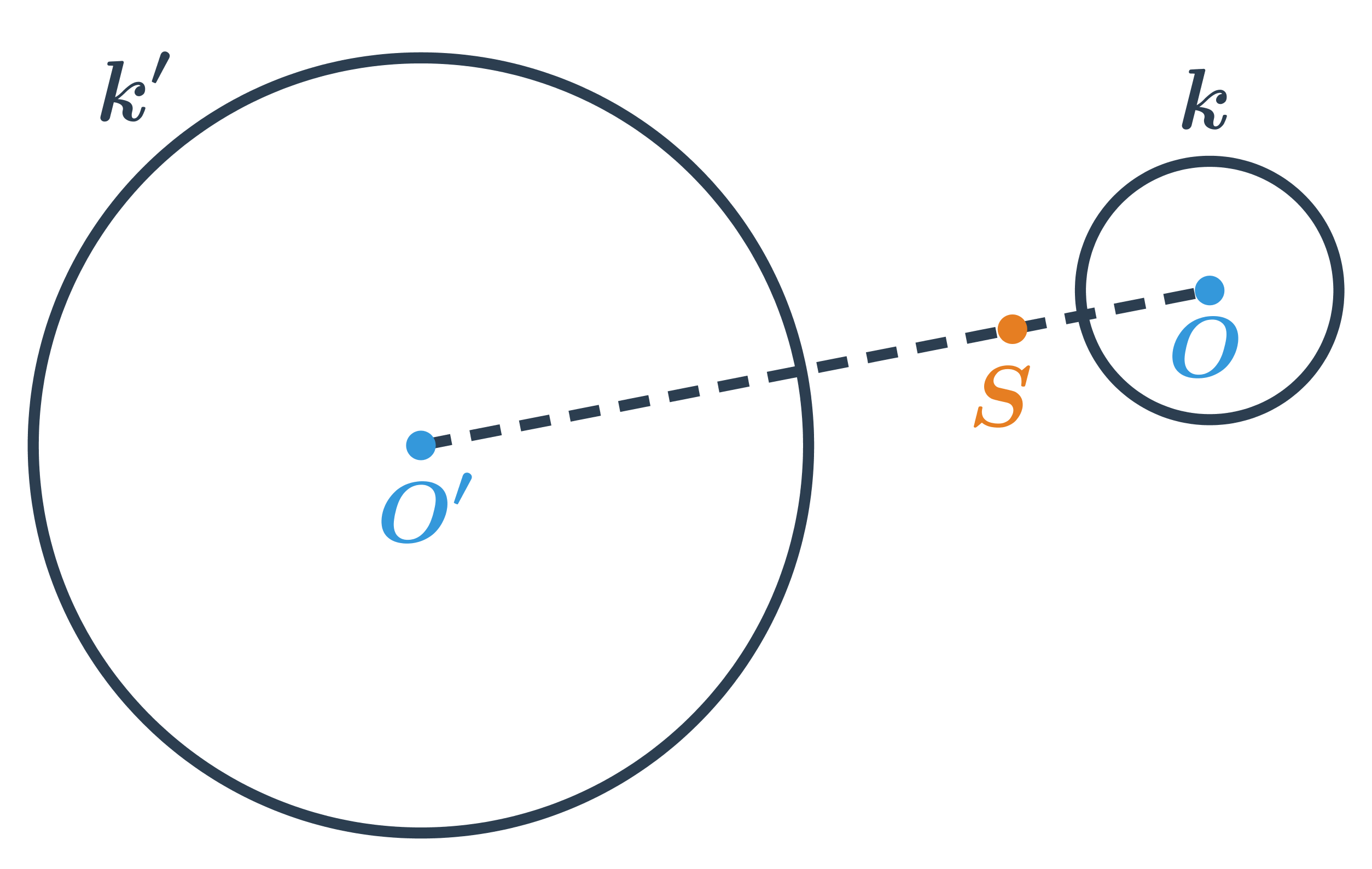
Stejnolehlost zachovává úhly a poměr délek, jde tedy o druh podobnosti.

Výpis souhrnů

Stejnolehlost

Podtémata

Stejnolehlost

Děkujeme za vaši zprávu, byla úspěšně odeslána.

Napište nám

Nevíte si rady?

Čeho se zpráva týká?