Výpis souhrnů

Grafy logaritmických funkcí

Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.

« Zpět na procvičování

Podtémata

Grafy logaritmických funkcí

Grafy logaritmických funkcí

Přejít ke cvičením na toto téma »

Logaritmická funkce je inverzní k exponenciální funkci o stejném základu. Grafy dvou navzájem inverzních funkcí jsou osově souměrné podle osy prvního kvadrantu (tj. přímky splňující x=y).

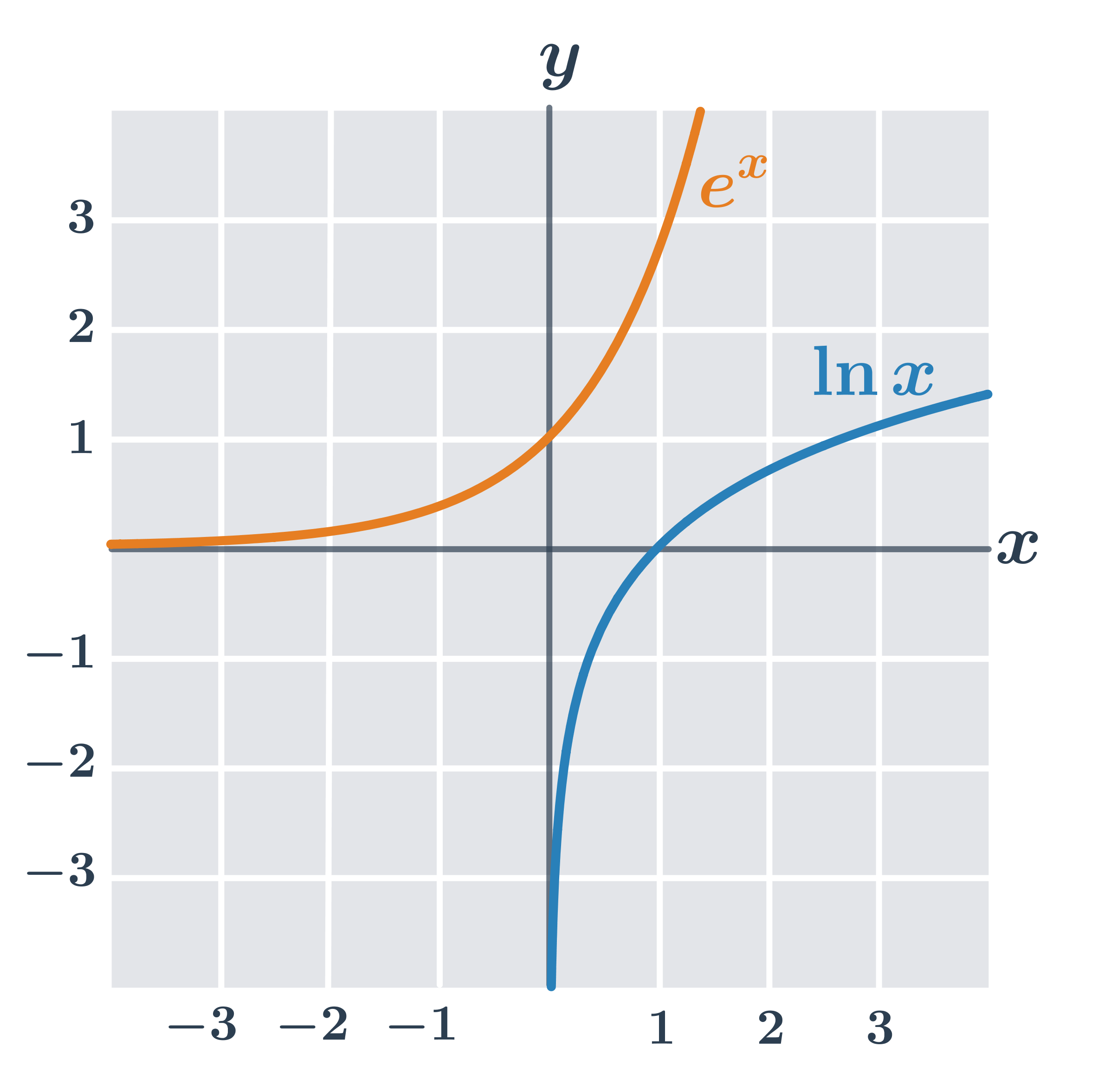
Graf každé logaritmické funkce tvaru y=\log_a x prochází bodem [1,0], protože pro libovolnou konstantu a platí: \log_a 1=0. Na obrázku vidíme grafy logaritmických funkcí s různými základy 2, e, 10.

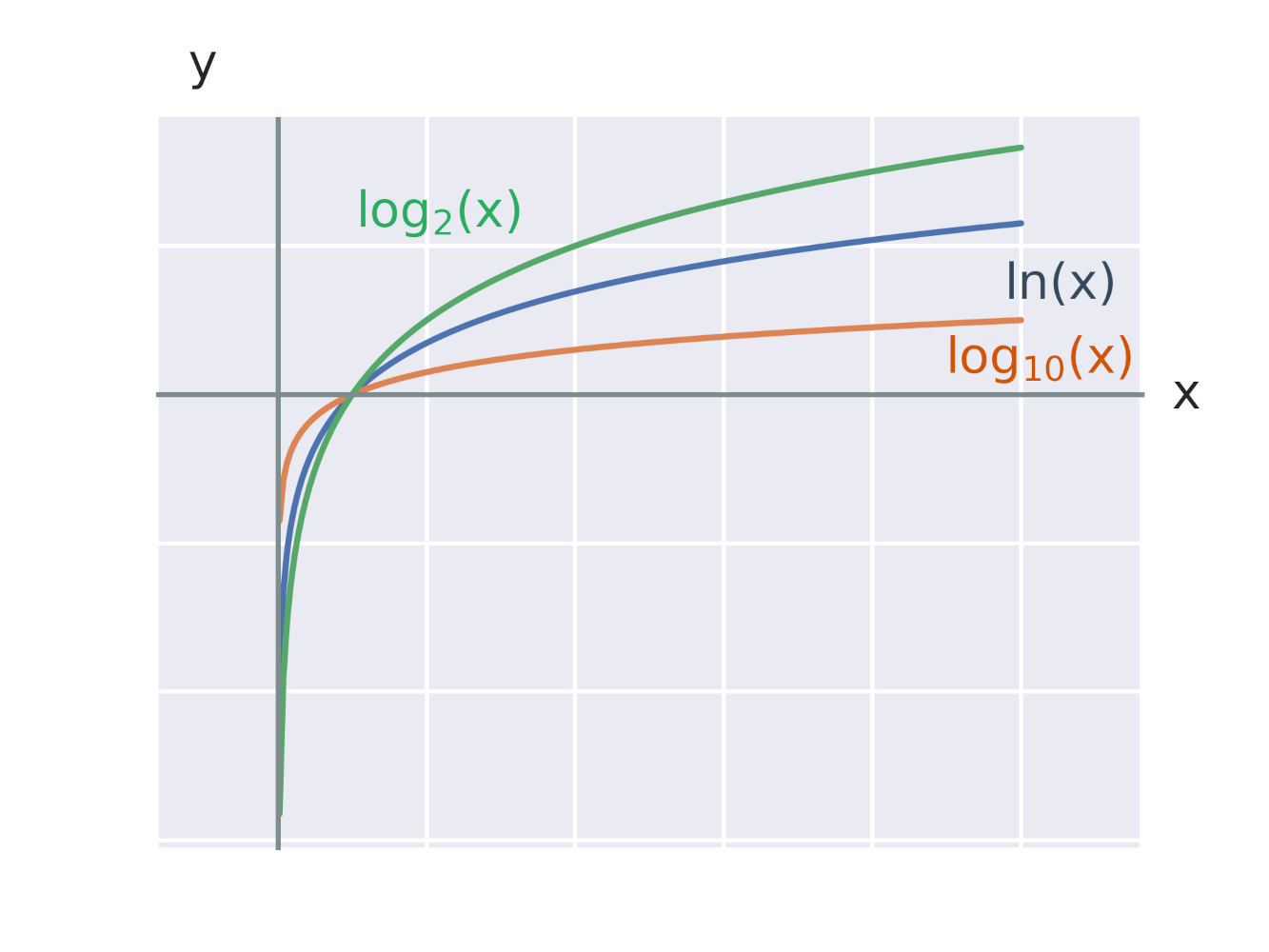
Značení některých význačných logaritmických funkcí:

funkce	popis	další možná značení
\log_a x	obecně logaritmus x o základu a pro nějaké a >0, a\neq 1
\ln x	přirozený logaritmus x, tj. logaritmus x o základu e	v angl. textech někdy \log x
\log x	dekadický logaritmus x, tj. logaritmus x o základu 10	\log_{10}x
\log_2 x	binární logaritmus x, tj. logaritmus x o základu 2	někdy se objevuje \mathrm{lb}\;x

Efekt přičtení konstanty k logaritmické funkci

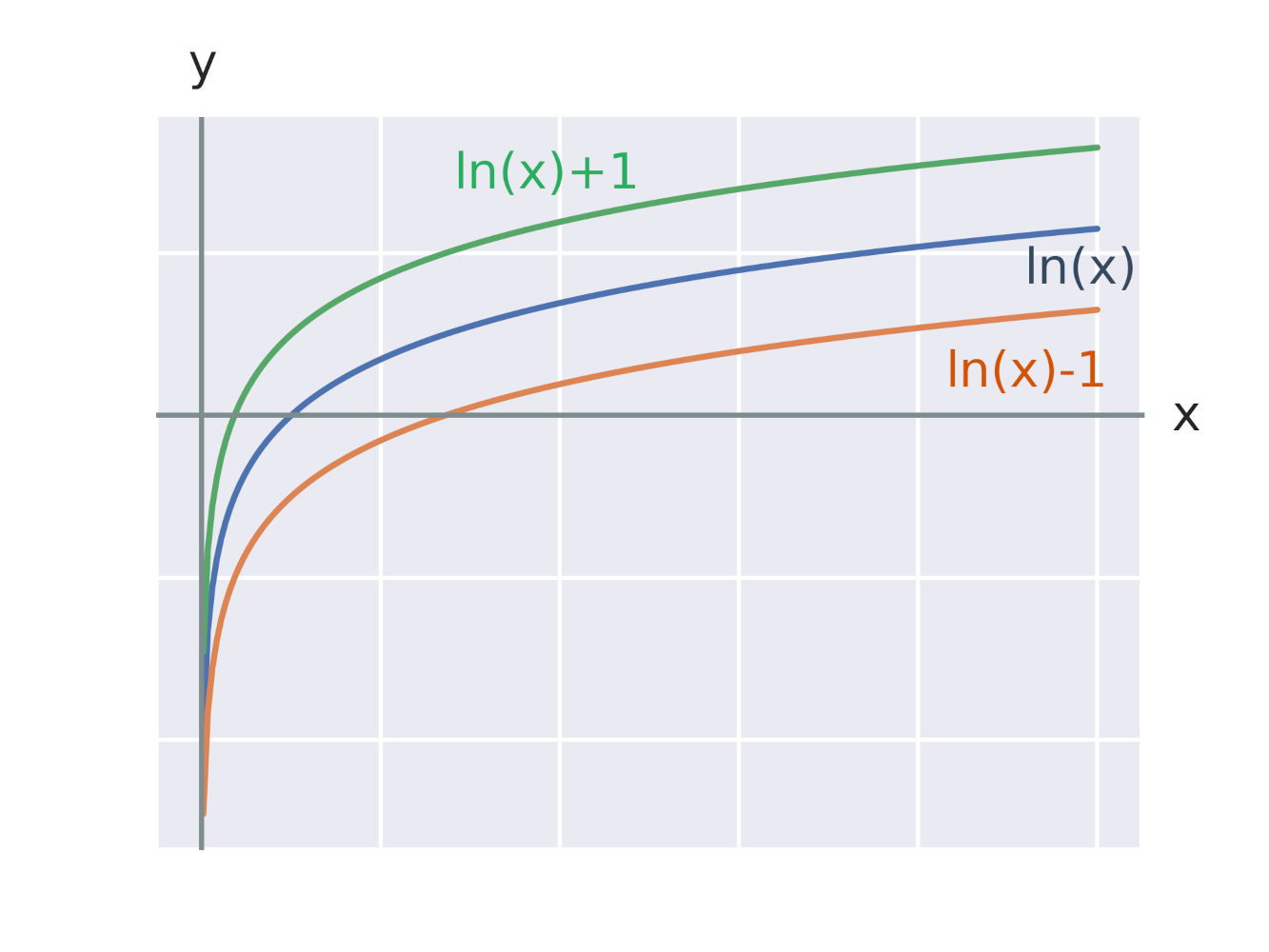
Efekt přičtení konstanty k argumentu logaritmické funkce

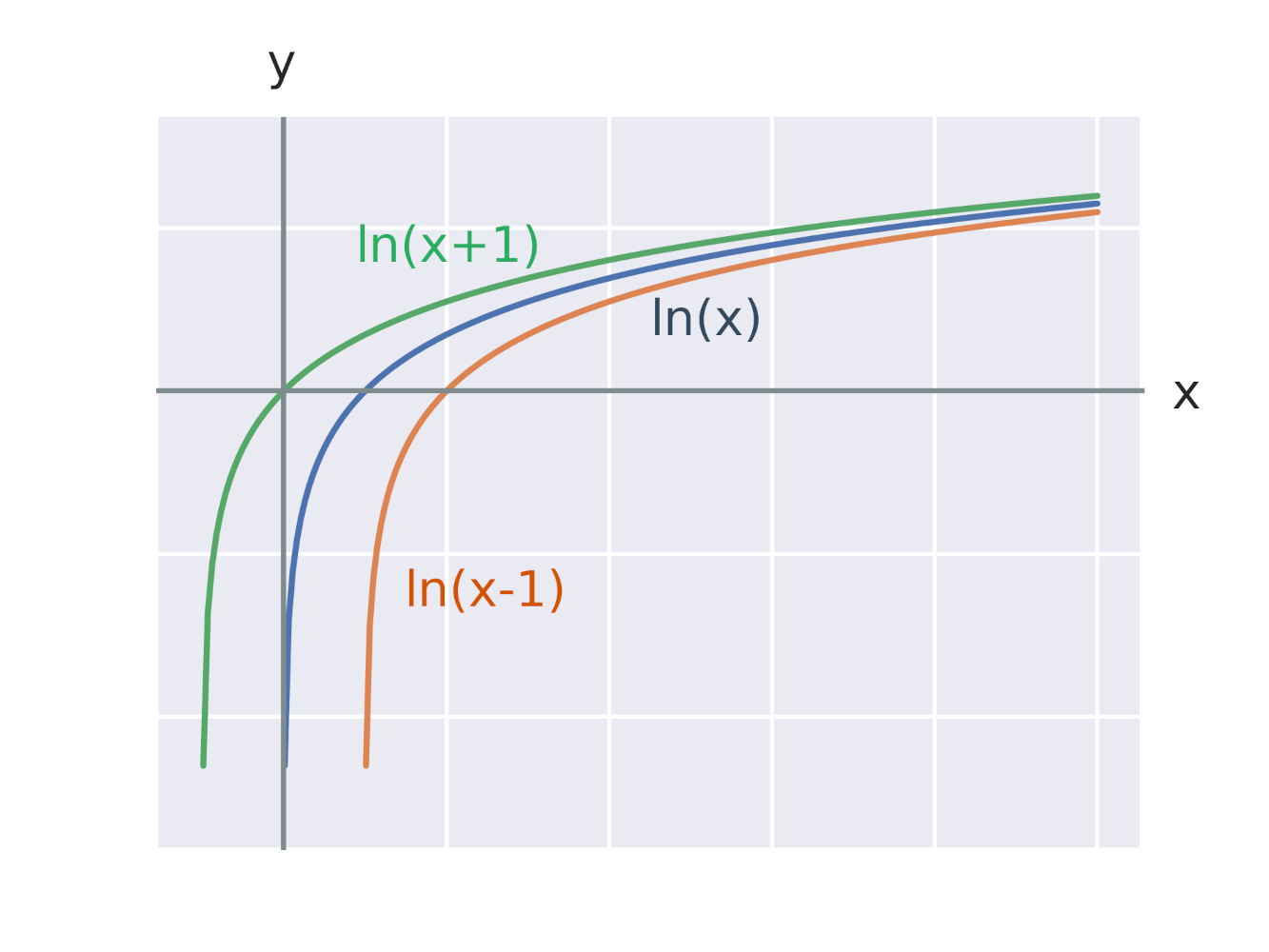
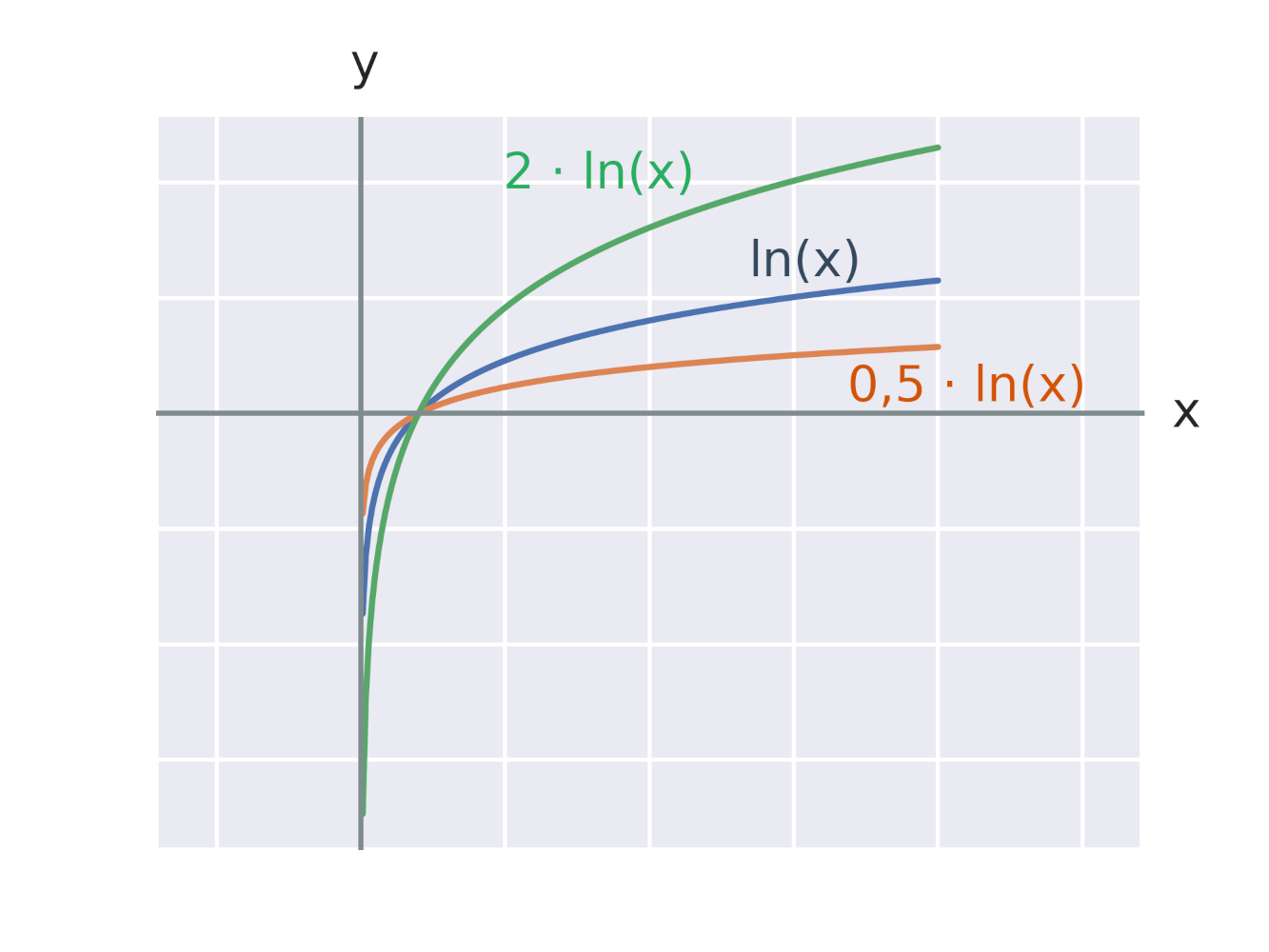
Efekt vynásobení logaritmické funkce konstantou

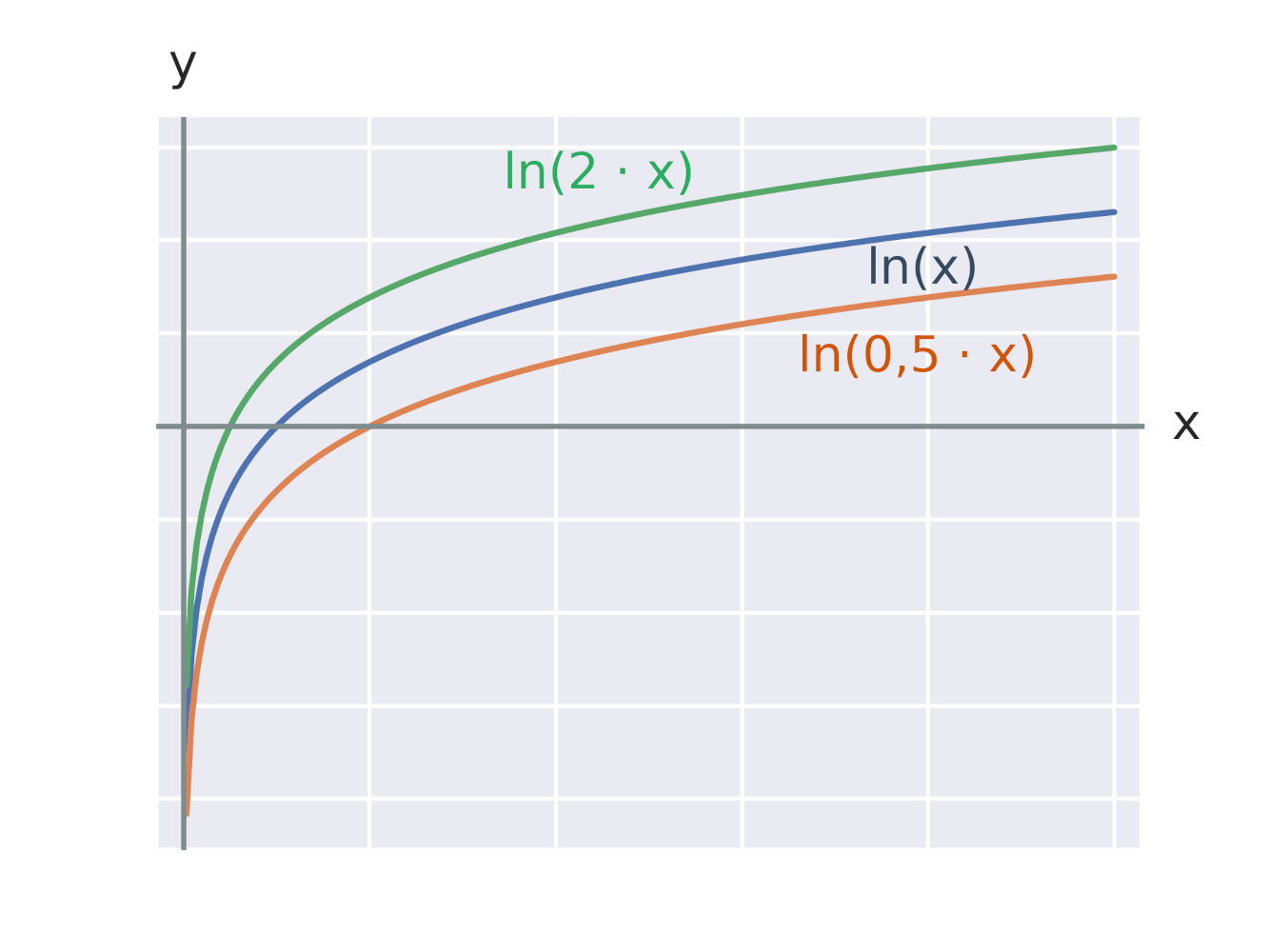
Efekt vynásobení argumentu logaritmické funkce konstantou

Výpis souhrnů

Grafy logaritmických funkcí

Podtémata

Grafy logaritmických funkcí

Děkujeme za vaši zprávu, byla úspěšně odeslána.

Napište nám

Nevíte si rady?

Čeho se zpráva týká?