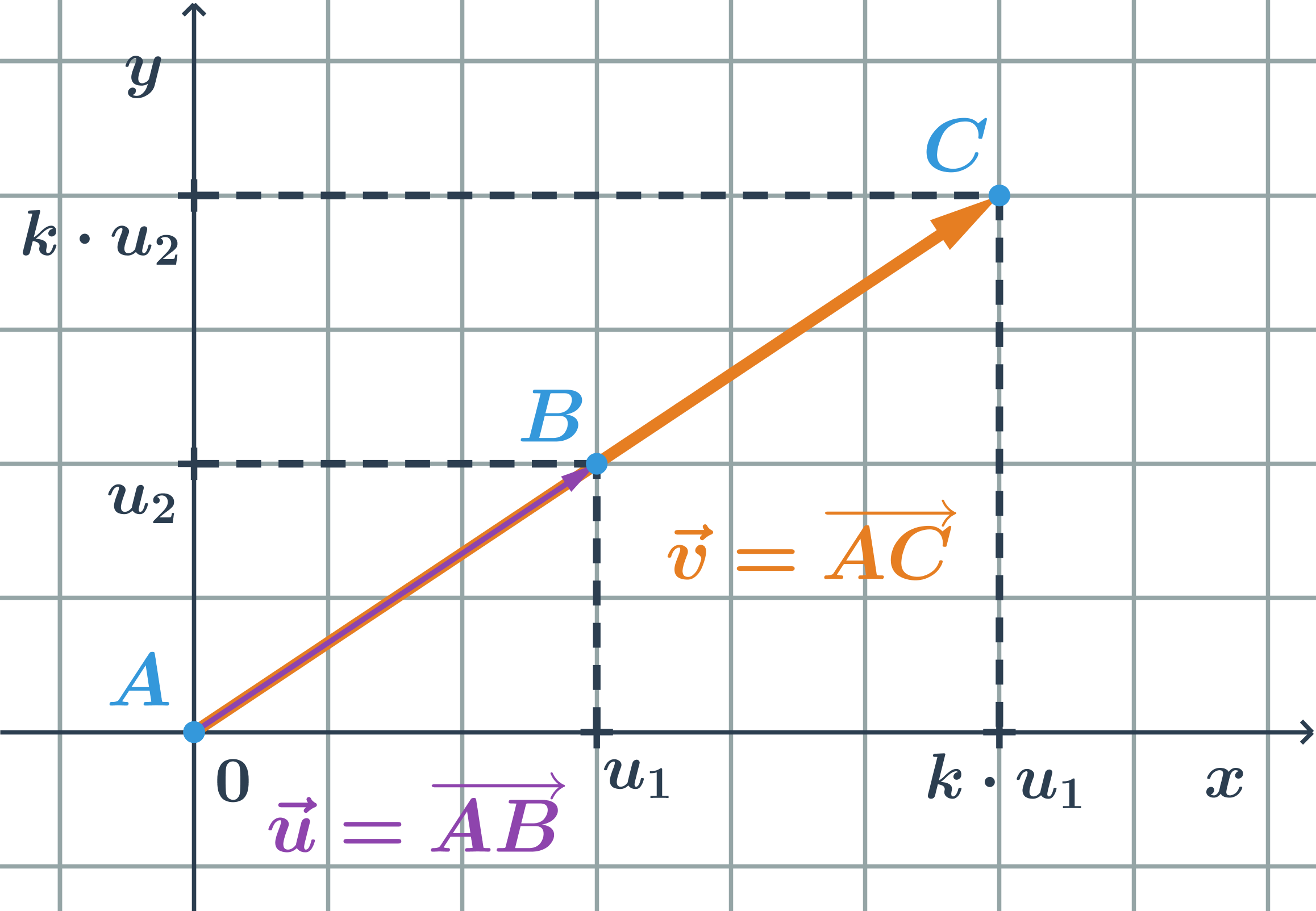Vzájemná poloha vektorů

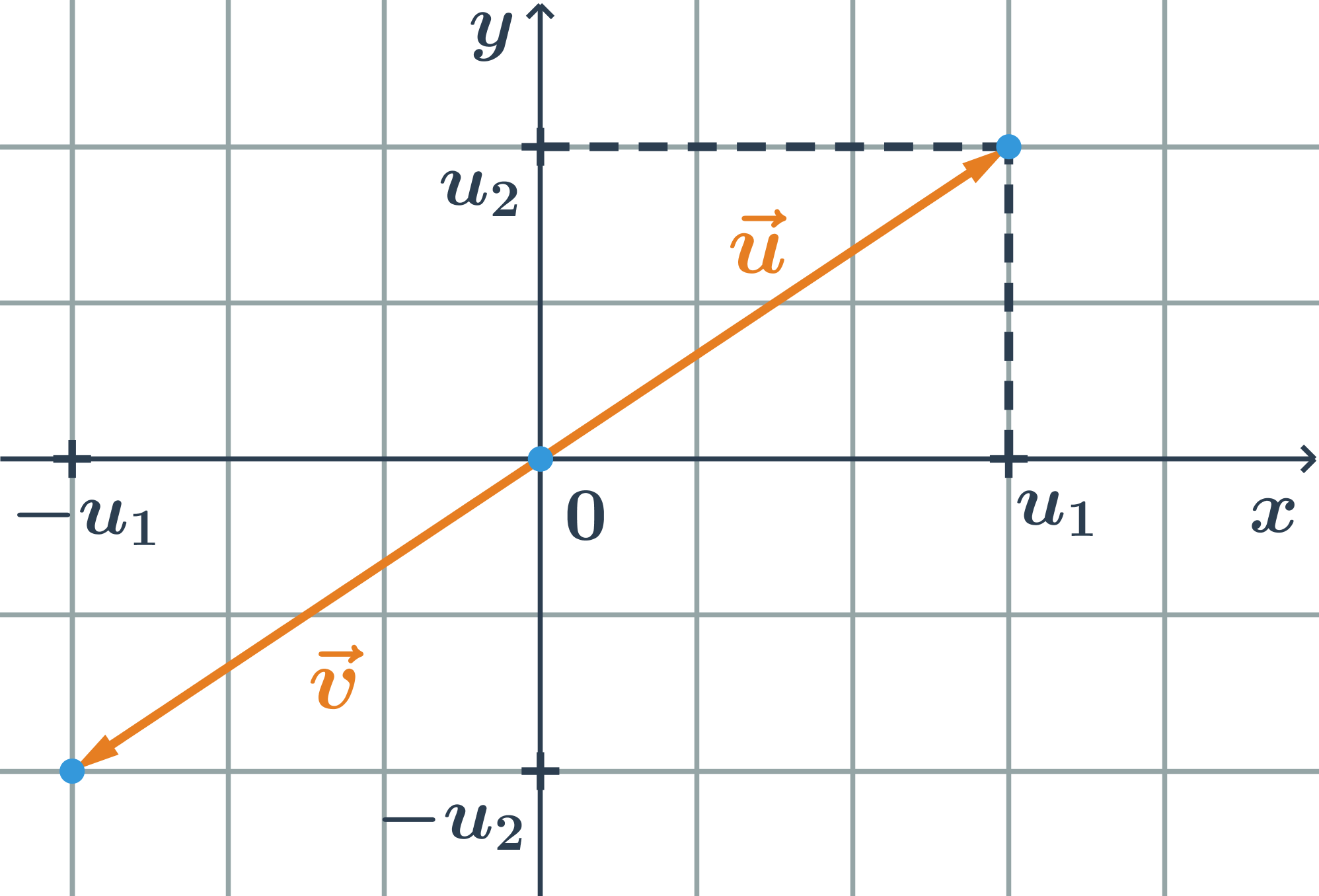
Opačné vektory jsou vektory, které mají stejnou délku a opačnou orientaci. K vektoru \vec{u}=(u_1;u_2) je opačný vektor \vec{v}=(-u_1;-u_2)
Příklad opačný vektor
- Určete opačný vektor k vektoru \vec{u}=(3;-1).
- Opačný vektor \vec{v} k vektoru \vec{u} má souřadnice: (-u_1;-u_2)=(-3;1)
Kolineární vektory jsou vektory, které můžeme umístit na jednu přímku. S vektorem \vec{u}=(u_1;u_2) je kolineární každý vektor \vec{v}=(k\cdot u_1;k \cdot u_2), kde k je reálné nenulové číslo. Pro k \gt 0 vektory mají stejný směr, pro k \lt 0 mají vektory opačný směr.
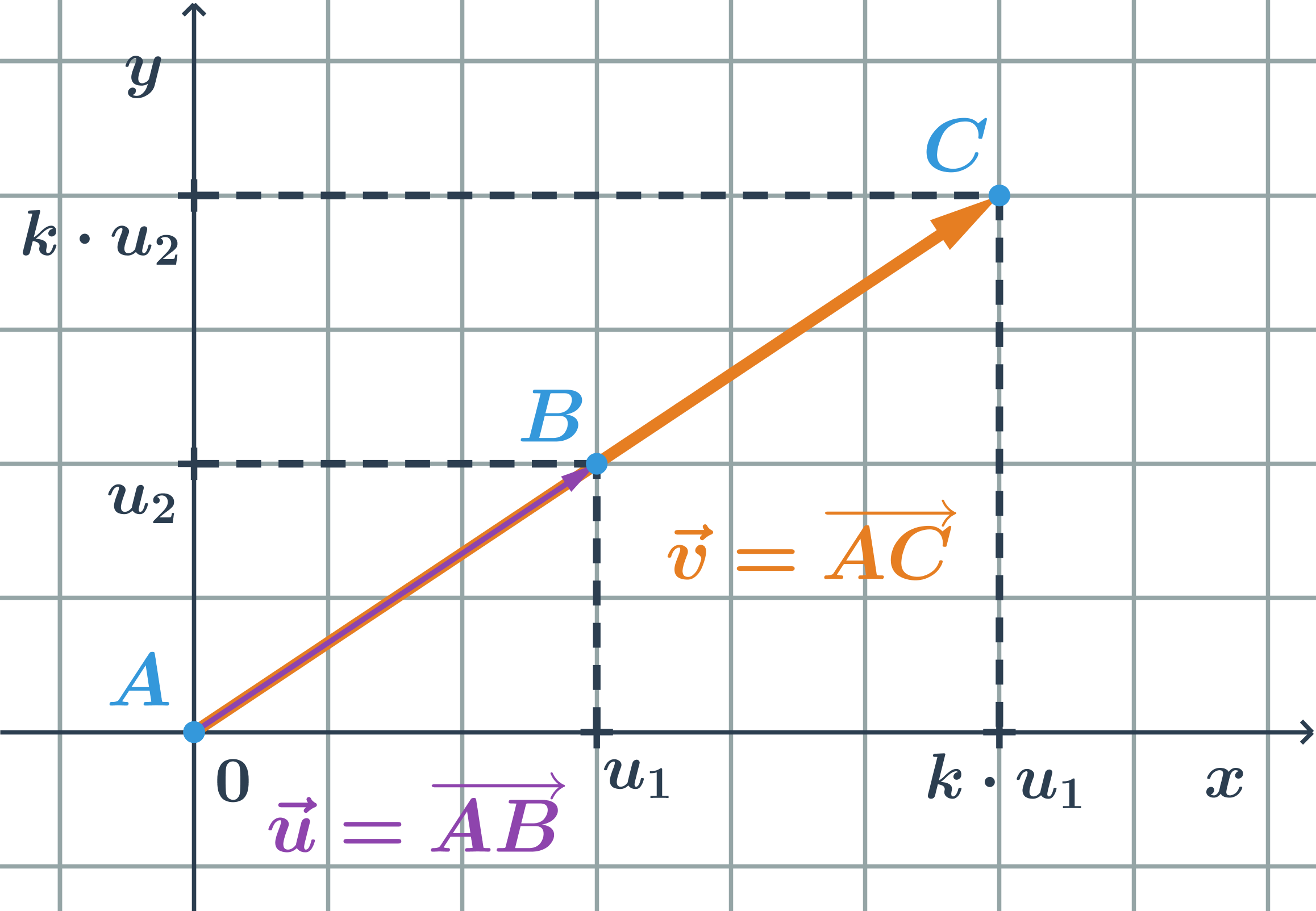
Příklad kolineární vektor
- Doplňte souřadnici vektoru \vec{v}=(v_1;3) tak, aby byl kolineární s vektorem \vec{u}=(2;-1).
- Pro druhou souřadnici platí: v_2=3, u_2=-1, tedy v_2= (-3) \cdot u_2
- Vidíme, že k=-3 je záporné, tj. \vec{u} a \vec{v} mají opačnou orientaci
- Pro první souřadnici musí platit: v_1= (-3) \cdot u_1= (-3)\cdot2=-6.
Kolmé vektory jsou vektory, které svírají pravý úhel K vektoru \vec{u}=(u_1;u_2) je kolmý každý vektor \vec{v}=(-k\cdot u_2;k \cdot u_1), kde k je reálné nenulové číslo.
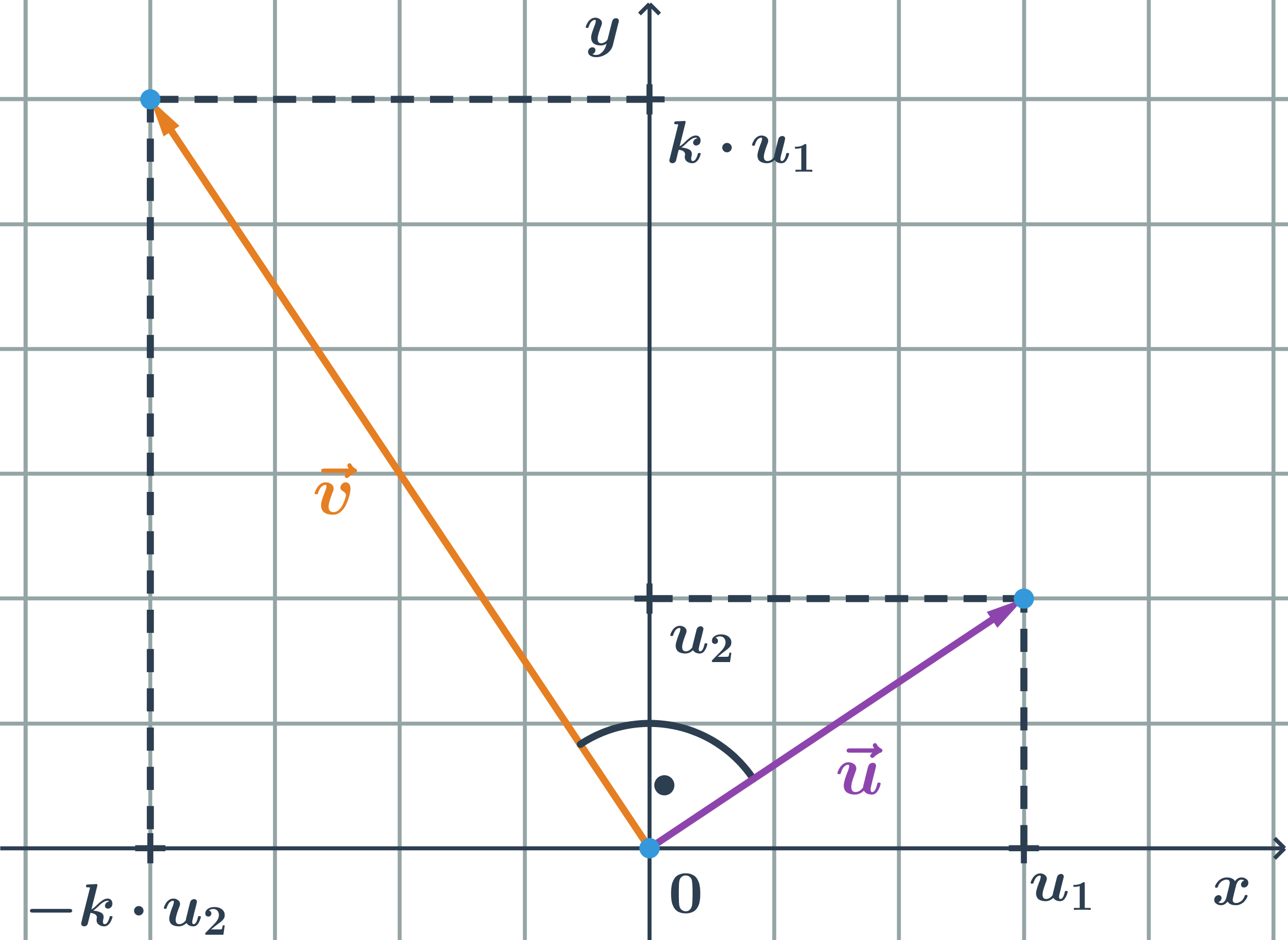
Příklad kolmý vektor
- Doplňte souřadnici vektoru \vec{v}=(v_1;4) tak, aby byl kolmý k vektoru \vec{u}=(2;-1).
- Platí: v_2=2 \cdot u_1, tedy musí platit: v_1 = - 2 \cdot u_2.
- Máme tedy v_1 = - 2 \cdot u_2 = -2 \cdot (-1) = 2.
Zavřít