
Odchylka dvou přímek

Odchylka rovnoběžek je 0^\circ. Odchylka různoběžek je velikost ostrého nebo pravého úhlu, který přímky svírají.
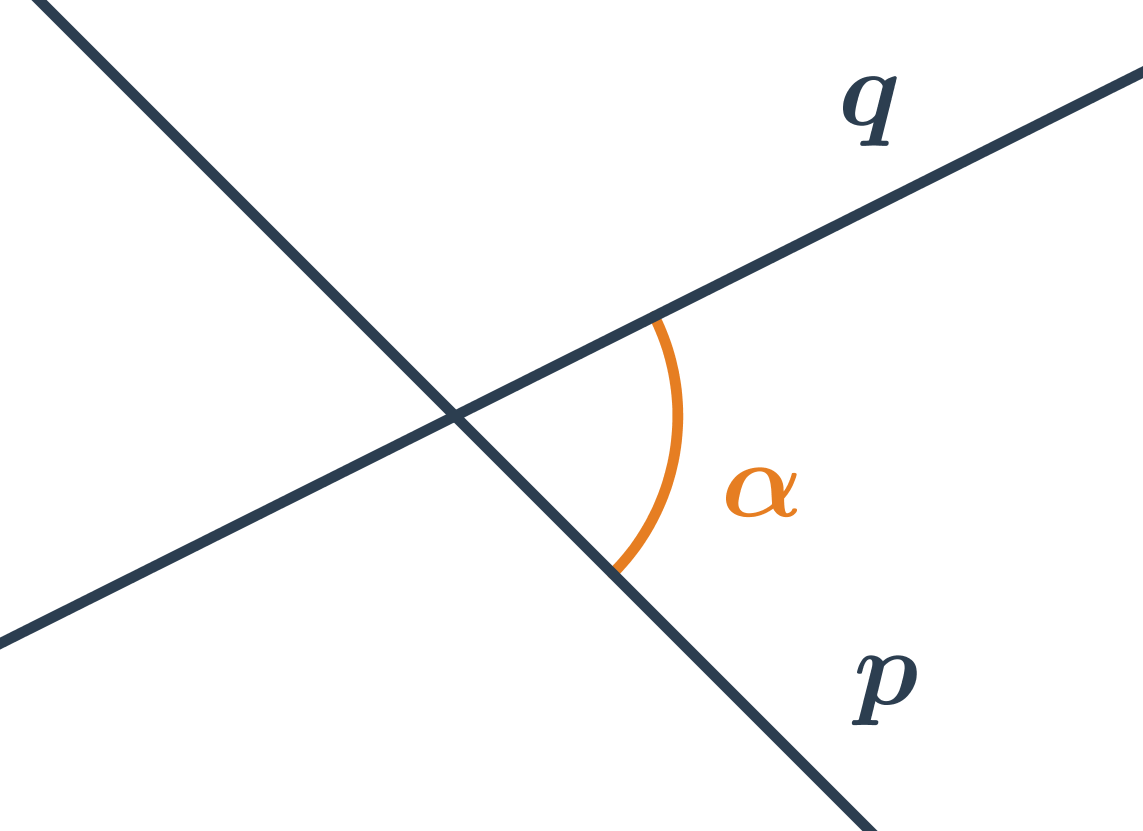
Odchylku různoběžek p a q můžeme vypočítat na základě znalosti směrových nebo normálových vektorů přímek. Vzorec pro výpočet úhlu různoběžek je obdobný jako vzorec pro výpočet úhlu vektorů
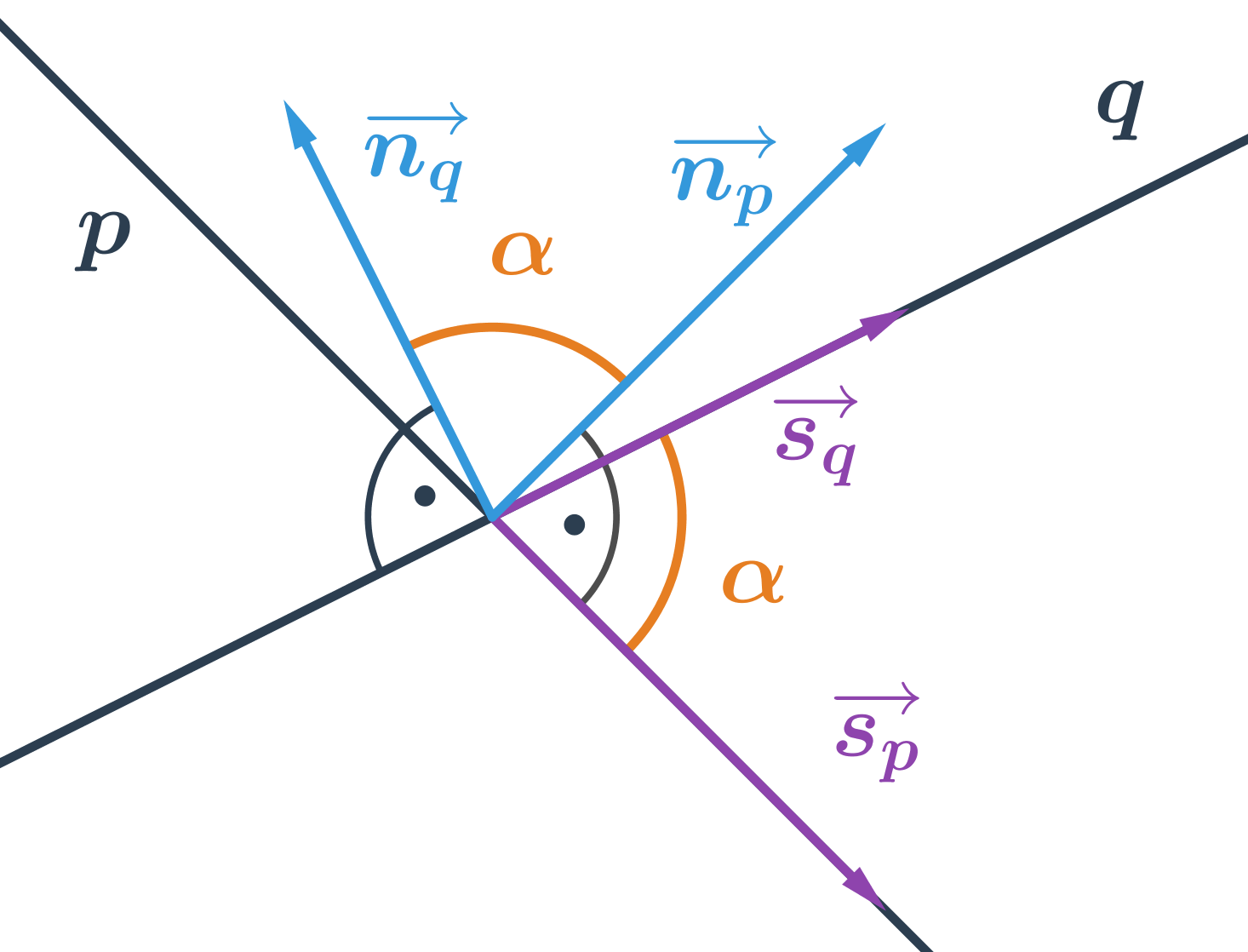
Odchylka různoběžek je úhel \alpha, pro který platí: \cos \alpha =\frac{\left| \vec{u} \cdot \vec{v} \right|}{\left| \vec{u} \right|\cdot \left| \vec{v} \right|} Vektory \vec{u} a \vec{v} uvedené ve vzorci jsou směrové vektory \overrightarrow{s_p} a \overrightarrow{s_q} nebo normálové vektory \overrightarrow{n_p} a \overrightarrow{n_q} přímek p a q.
Pro dvě k sobě kolmé přímky platí, že jejich odchylka \alpha=90^\circ a tedy \cos\alpha=0.
Proč musí být ve vzorci pro výpočet odchylky přímek absolutní hodnota?
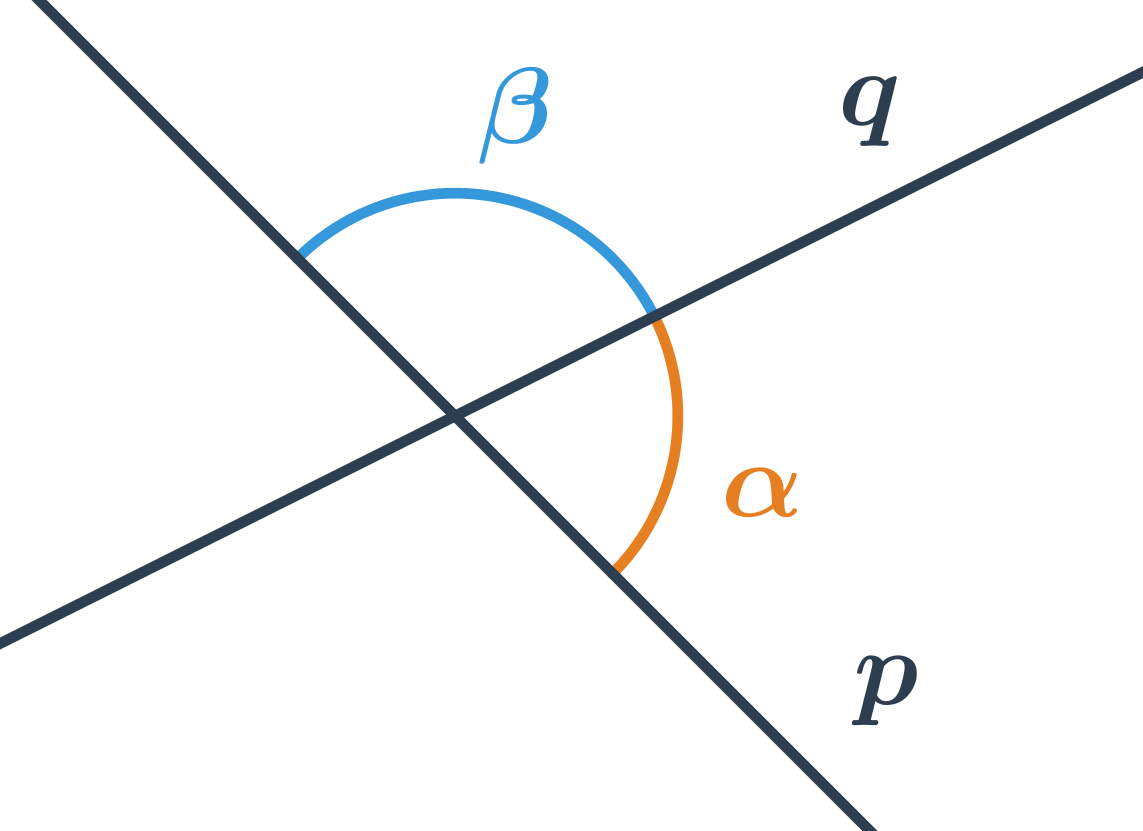
- Odchylka přímek p a q na obrázku je ostrý úhel \alpha, nikoliv tupý úhel \beta.
- \alpha a \beta jsou vedlejší úhly, pro které je hodnota funkce \cos opačná, tedy: \cos\alpha=-\cos\beta
- Pro úhel \alpha je \cos\alpha \gt 0, pro \beta je $$
- Absolutní hodnota ve vzorci nám zaručí, že najdeme úhel, kde hodnota funkce \cos je kladná, tedy úhel ostrý, který je odchylkou daných přímek.
Odchylka přímek a úhly v trojúhelníku
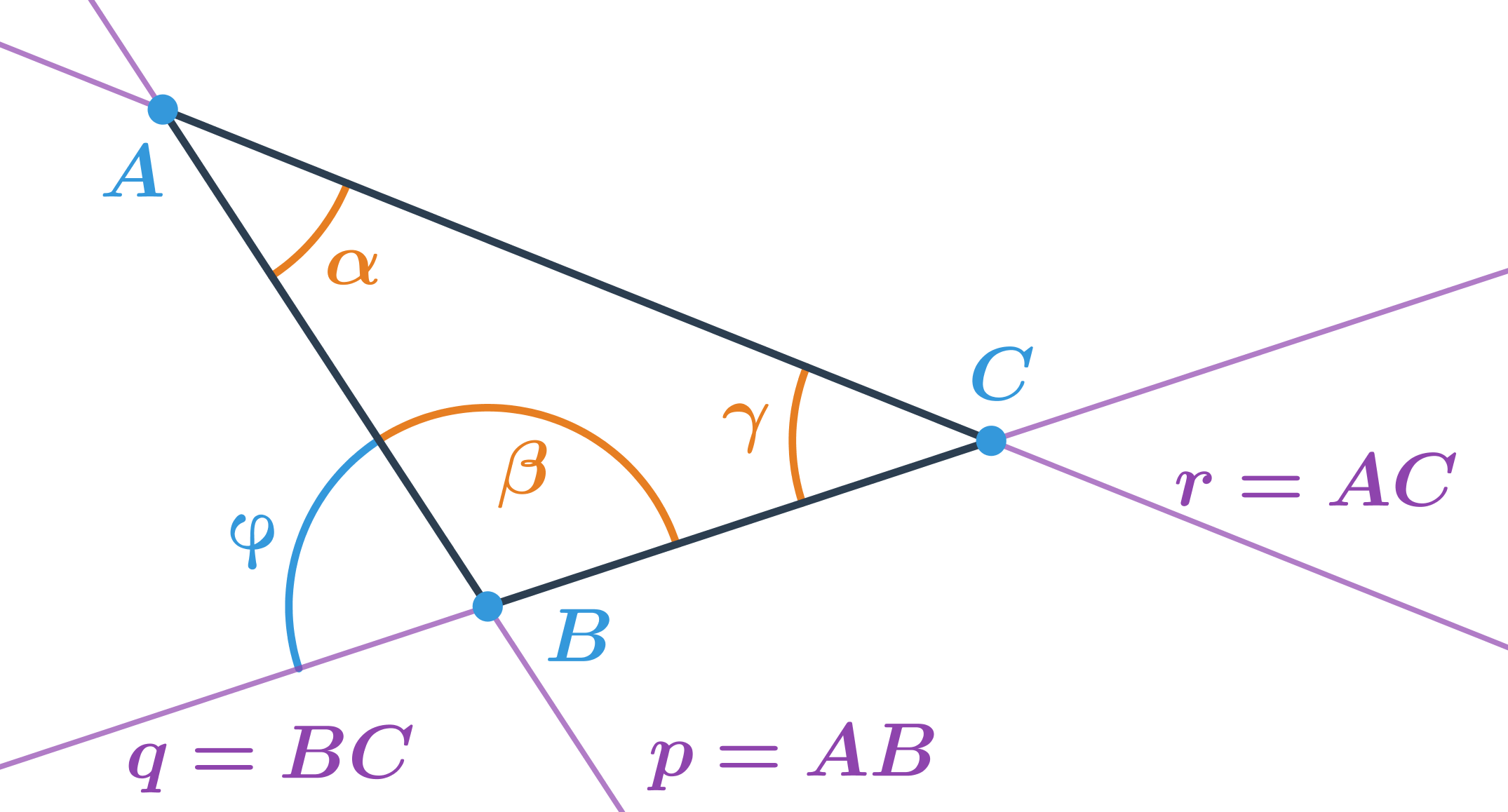
V trojúhelníku na obrázku:
- úhel \alpha je menší než 90^\circ a je to odchylka přímek AB a AC
- úhel \beta je větší než 90^\circ a není to odchylka přímek AB a BC
- úhel \gamma je menší než 90^\circ a je to odchylka přímek BC a AC
Velikost úhlů v trojúhelníku nemusí být stejná jako odchylka přímek, na kterých leží strany trojúhelníku. Úhly v trojúhelníku počítáme jako odchylku vektorů, které určují daný úhel. Tento úhel může být větší než 90^\circ, proto využijeme vzorec pro výpočet odchylky vektorů (ve vzorci nebude absolutní hodnota).
Odchylka přímek
Určete odchylku přímek p:x-2y+3=0 a q:2x-y+1=0
- Přímky jsou dané obecnými rovnicemi, proto pro výpočet jejich odchylky využijeme normálové vektory: \overrightarrow{n_p}=(1;-2) a \overrightarrow{n_q}=(2;-1)
- Dosadíme do vzorce: \cos \alpha =\frac{\left| \vec{u} \cdot \vec{v} \right|}{\left| \vec{u} \right|\cdot \left| \vec{v} \right|}=\frac{\left| 1\cdot2+(-2) \cdot(-1) \right|}{\sqrt{1^2+(-2)^2}\cdot\sqrt{2^2+(-1)^2}}=\frac{4}{\sqrt{5}\cdot \sqrt{5}}=\frac{4}{5}
- Pomocí funkce cos^{-1} na kalkulačce dopočítáme odchylku: \alpha=36^\circ
Zavřít













