
Vzdálenost bodu od přímky

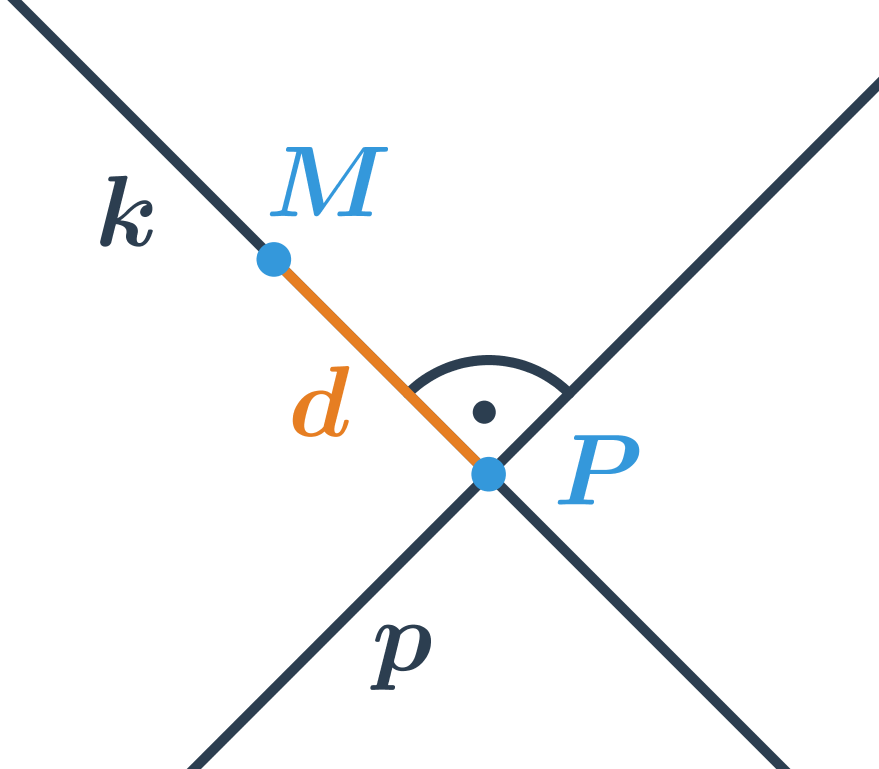
Vzdálenost bodu od přímky je délka nejkratší úsečky určené bodem M a bodem ležícím na přímce p. Jak je vidět z obrázku tato nejkratší úsečka leží na kolmici z bodu M k přímce p. Vzdálenost bodu od přímky tedy můžeme určit takto:
- najdeme přímku k, která prochází bodem M a je kolmá k přímce p
- určíme průsečík P přímky k s přímkou p
- vzdálenost bodu M od přímky p je délka úsečky PM
Příklad: vzdálenost bodu od přímky – pomocí kolmice
Určete vzdálenost bodu M=[5;2] od přímky p:4x+3y-1=0.
- Přímka k, která prochází bodem M a je kolmá k přímce p má směrový vektor kolineární s normálovým vektorem přímky p.
- Souřadnice směrového vektoru přímky k jsou: \vec{u}=(4;3).
- Přímka k má parametrické vyjádření: p:X=M+t\vec{u}
- p:\begin{array}{rrl}x&=&5+4t\\y&=&2+3t\\&&t\in\mathbb{R}\end{array}
- Souřadnice průsečíku P přímky k s přímkou p určíme dosazením parametrického vyjádření přímky k do obecné rovnice přímky p.
\begin{array}{rrl}4(5+4t)+3(2+3t)-1&=&0\\20+16t+6+9t-1&=&0\\25+25t&=&0\Rightarrow t=-1\end{array}
- Průsečík přímek k a p je bod P=[1;-1].
- Vzdálenost bodu M od přímky p je délka úsečky PM:
- Vzorec pro délku úsečky: d=\sqrt{(x_M-x_P)^2+(y_M-y_P)^2}
- Dosadíme souřadnice bodů M,P: d=\sqrt{(5-1)^2+(2-(-1))^2}=\sqrt{16+9}=5
Vzorec pro vzdálenost bodu od přímky dané obecnou rovnicí
Vzdálenost bodu M=[m_1;m_2] od přímky p dané obecnou rovnicí ax+by+c=0 je dána vzorcem: d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}}
Příklad: vzdálenost bodu od přímky – pomocí vzorce
Určete vzdálenost bodu M=[5;2] od přímky p:4x+3y-1=0 s využitím vzorce.
- Dosadíme do vzorce d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}} souřadnice bodu M=[5;2] a koeficienty a a b z obecné rovnice přímky.
- Obecná rovnice pro p je 4x+3y-1=0, tedy a=4 a b=3.
- Máme: d=\frac{\left| 4\cdot5+3\cdot2-1\right|}{\sqrt{4^2+3^2}}=\frac{25}{\sqrt{25}}=5
Vzdálenost dvou rovnoběžek
Umíme-li určit vzdálenost bodu od přímky, snadno určíme také vzdálenost dvou rovnoběžek. Stačí si uvědomit, že všechny body ležící na jedné přímce mají od druhé přímky stejnou vzdálenost. Proto je vzdálenost rovnoběžek stejná jako vzdálenost libovolného bodu na jedné přímce od přímky druhé.
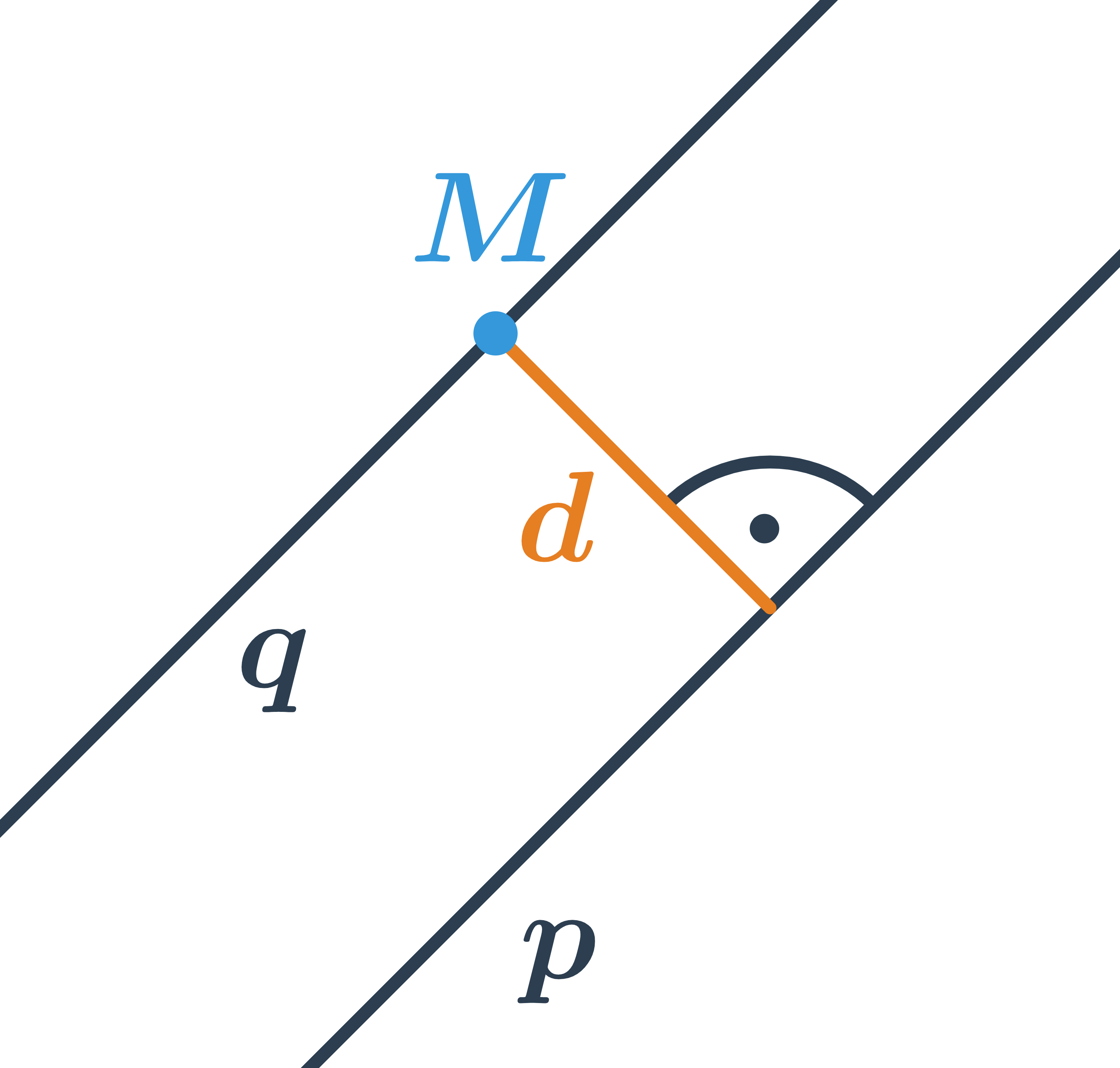
Příklad: vzdálenost rovnoběžek
Určete vzdálenost rovnoběžek p:2x-4y+3=0 a q:x-2y+1=0.
- Určíme souřadnice jednoho bodu (M) na přímce q tak, že jednu souřadnici zvolíme a druhou dopočítáme.
- Zvolíme například souřadnici y=0, pak x-2\cdot0+1=0\Rightarrow x=-1
- Dosadíme do vzorce d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}} souřadnice bodu M=[-1;0] a koeficienty a a b z obecné rovnice přímky p.
- Obecná rovnice pro p je 2x-4y+3=0, tedy a=2 a b=-4.
- Máme: d=\frac{\left| 2\cdot(-1)-4\cdot0+3\right|}{\sqrt{2^2+(-4)^2}}=\frac{1}{\sqrt{20}}
- Vzdálenost rovnoběžek p a q je: d=\frac{1}{\sqrt{20}}
Zavřít











