Vlastnosti goniometrických funkcí

Pro obě funkce \sin x a \cos x platí:

• definiční obor je množina reálných čísel,
• obor hodnot je interval \langle -1, 1 \rangle,
• funkce je omezená,
• funkce je periodická s periodou 2\pi,
• funkce není prostá.

Pro funkci \sin x platí:

• je lichá,
• hodnoty nula nabývá v bodech x=k\pi.

Pro funkci \cos x platí:

• je sudá,
• hodnoty nula nabývá v bodech x=(2k+1)\frac{\pi}{2}.

Pro funkci \tan x platí:

• definiční obor je \{x \in \mathbb{R}: x \neq (2k+1)\frac{\pi}{2} \},
• obor hodnot je množina reálných čísel,
• funkce je lichá,
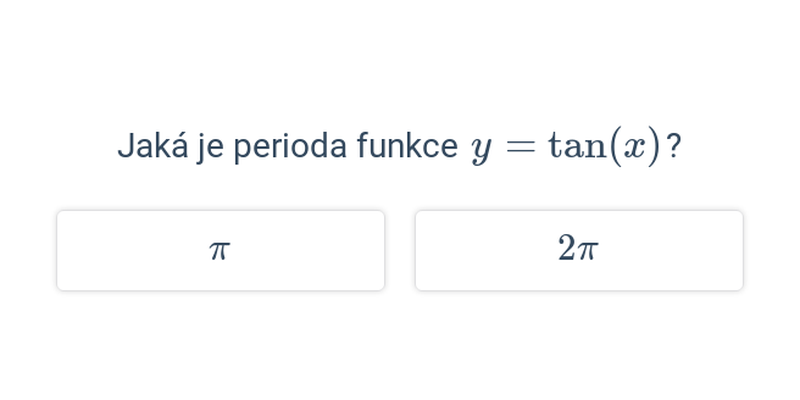
• funkce je periodická s periodou \pi,
• funkce je neomezená,
• hodnoty nula nabývá v bodech x=k\pi.