Obsah, obvod: kruh, kružnice

Vzorce

Obvod kruhu (i kružnice) o poloměru r je o=2\pi r. Pro průměr d platí o = \pi d.

Obsah kruhu o poloměru r je S=\pi r^2. Pro průměr d platí S = \frac{1}{4} \pi d^2.

Konstanta \pi se nazývá též Ludolfovo číslo. \pi je iracionální číslo, což znamená, že nejde vyjádřit zlomkem ani zapsat přesně v desítkové soustavě. Přibližná hodnota \pi je 3,14159265.

Při výpočtu obsahu a obvodu kruhu dáváme dobrý pozor na to, zda vycházíme ze znalosti poloměru nebo průměru. Záměna průměru za poloměr je častou chybou.

Intuice

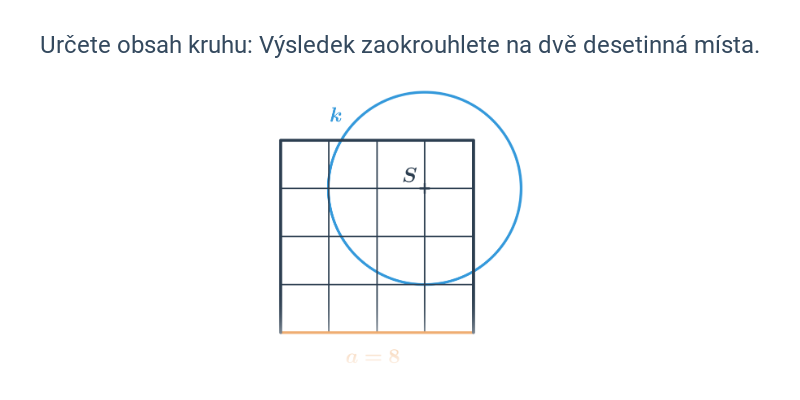
Základní intuici za vzorci pro výpočet obsahu a obvodu kruhu přibližuje níže uvedený obrázek. Žluté čtverce mají obsah r^2. Oranžový čtverec se skládá ze čtyř žlutých čtverců, takže má obsah 4\cdot r^2. Kruh má „o trochu menší“ obsah než oranžový čtverec, což odpovídá tomu, že obsah kruhu je přibližně 3{,}14 \cdot r^2. Obvod oranžového čtverce je 8\cdot r. Obvod kruhu je opět „o trochu menší“ – je to 2\pi \cdot r \approx 6{,}3 \cdot r.

Příklady

• Mějme kruh o poloměru 3 cm. Jeho obvod je 2\pi \cdot 3 \approx 2 \cdot 3{,}14 \cdot 3 \approx 18{,}8 cm. Jeho obsah je \pi \cdot 3^2 \approx 3{,}14\cdot 9 \approx 28,3 cm².
• Kružnice o průměru 2 cm má obvod \pi \cdot 2 \approx 6,3 cm. Její vnitřek má obsah \frac{1}{4} \pi \cdot 2^2 = \pi \approx 3,14 cm².
• Středový kruh na fotbalovém hřišti má poloměr 9{,}1 metru. Pokud jej chceme obejít po jeho okrajové čáře, ujdeme 2 \pi \cdot 9{,}1 \approx 57 metrů. Pokud bychom chtěli veškerou trávu v kruhu nabarvit na růžovo, museli bychom nabarvit \pi \cdot 9{,}1^2 \approx 260 m² trávy.