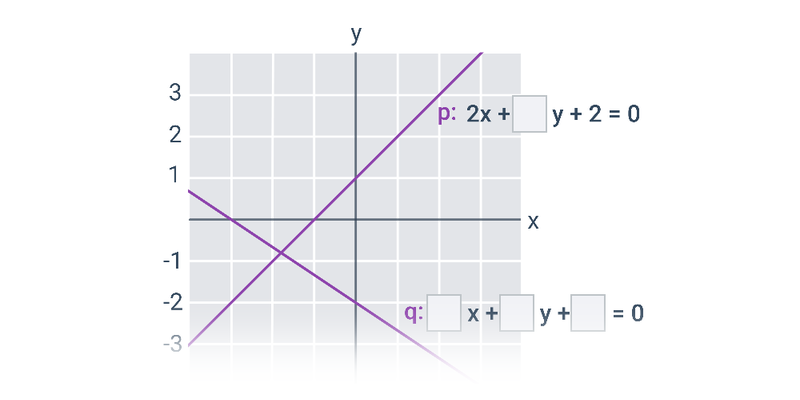
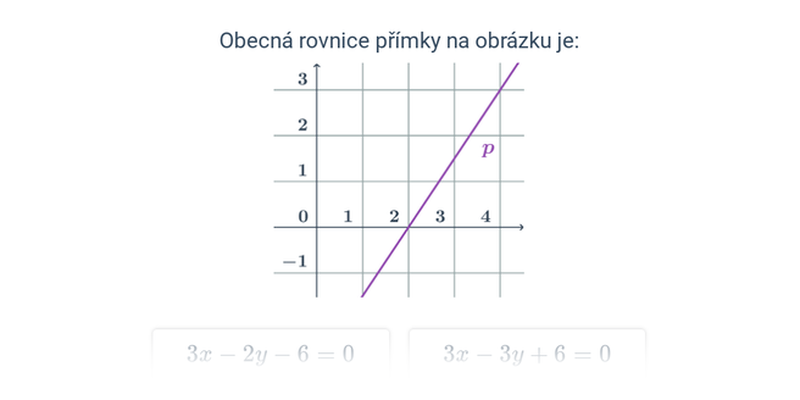
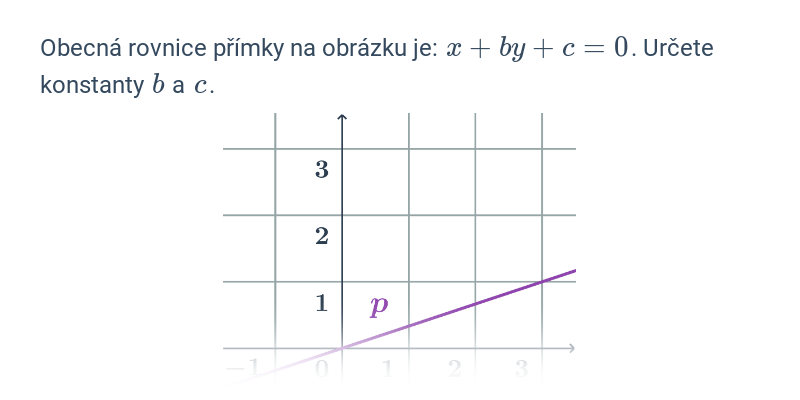Obecná rovnice přímky v rovině má tvar: ax+by+c=0, kde konstanty a a b jsou souřadnice normálového vektoru a c reálné číslo. Normálový vektor \vec{n}=(a;b) je vektor kolmý k dané přímce, tedy i kolmý ke směrovému vektoru přímky.
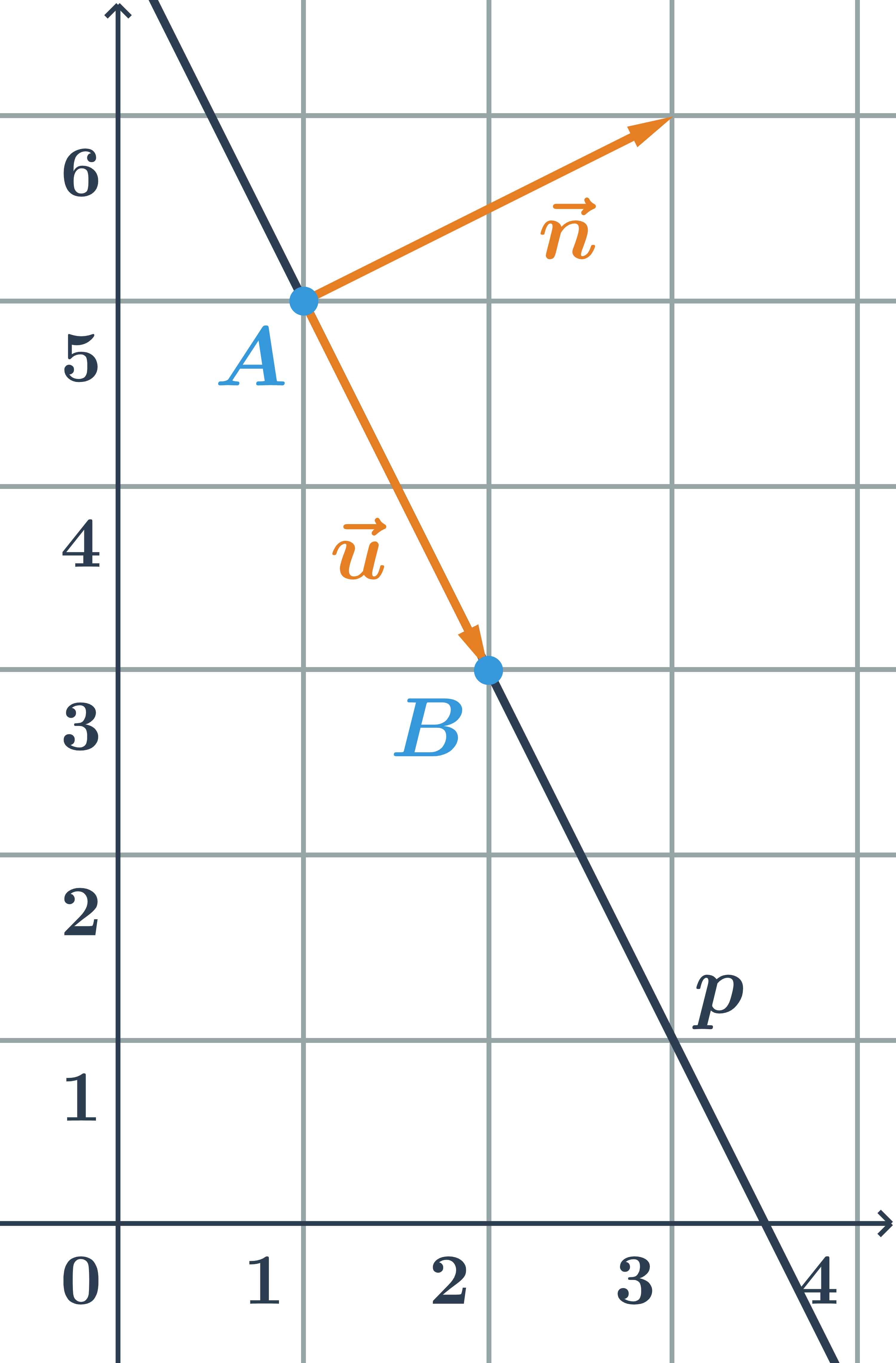
Obecná rovnice přímky p určené body A=[1;5] a B=[2;3]
- Přímka p je určená bodem A a směrovým vektorem \vec{u}=\overrightarrow{AB}=B-A=(1;-2).
- Normálový vektor je kolmý k vektoru \vec{u}=(1;-2), tedy například vektor \vec{n}=(2;1).
- Souřadnice normálového vektoru jsou konstanty a a b v obecné rovnici přímky. Obecná rovnice má tvar: 2x+y+c=0
- Konstantu c dopočítáme dosazením souřadnic bodu A=[1;5] :
- 2\cdot1+5+c=0\Rightarrow c=-7
- Obecná rovnice přímky p je: 2x+y-7=0
Obecná rovnice přímky dané parametricky
Určete obecnou rovnici přímky p, která je dána následující parametrickou soustavou rovnic: \begin{array}{rrl}x&=&1+2t\\y&=&4+6t\\&&t\in\mathbb{R}\end{array}
- Přímka p je určená bodem A=[1;4] a směrovým vektorem \vec{u}=(2;6).
- Souřadnice směrového vektoru můžeme upravit na tvar: \vec{u}=(1;3).
- Normálový vektor je kolmý k vektoru \vec{u}=(1;3), tedy například vektor \vec{n}=(3;-1).
- Souřadnice normálového vektoru jsou konstanty a a b v obecné rovnici přímky. Obecná rovnice má tvar: 3x-y+c=0
- Konstantu c dopočítáme dosazením souřadnic bodu A=[1;4] :
- 3\cdot1-4+c=0\Rightarrow c=1
- Obecná rovnice přímky p je: 3x-y+1=0
Parametrické vyjádření přímky dané obecnou rovnicí
Určete parametrické vyjádření přímky p, která má obecnou rovnici: 3x-2y+4=0.
- Přímka p má normálový vektor \vec{n}=(3;-2).
- Směrový vektor je kolmý k vektoru \vec{n}=(3;-2), tedy například vektor \vec{u}=(2;3).
- Určíme jeden bod na přímce p : jednu souřadnici můžeme zvolit, například x=0, druhou souřadnici dopočítáme: 3\cdot0-2y+4=0\Rightarrow y=2
- Z obecné rovnice jsme tedy zjistili, že na přímce leží bod A=[0;2].
- Parametrické vyjádření přímky p je: \begin{array}{rrl}x&=&0+2t\\y&=&2+3t\\&&t\in\mathbb{R}\end{array}
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.