Výpis souhrnů
Přímky
Podtémata
Přímka je jednoznačně určena bodem, který na ní leží a směrovým vektorem, což si můžete prakticky vyzkoušet v kapitole Určení přímky.
V rovině i v prostoru lze zapsat přímku jako množinu bodů, které splňují parametrickou rovnici. V rovině umíme pro danou přímku napsat také obecnou rovnici (ale v prostoru ne).
Máme-li přímku popsanou rovnicí, umíme určit vzájemnou polohu dvou přímek nebo vzájemnou polohu přímky a bodu výpočtem.
NahoruPřímky: pojmy
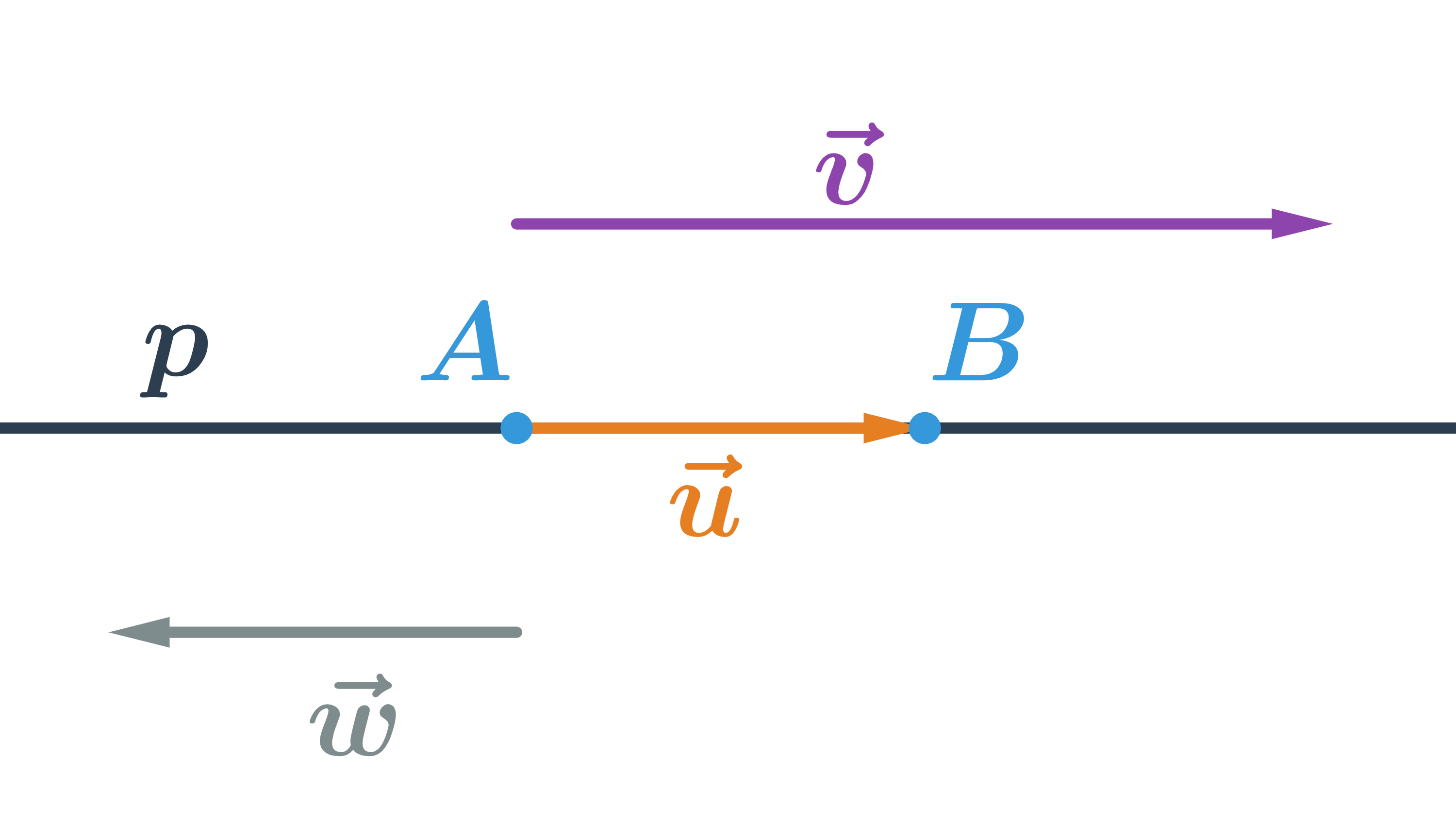
Přímka je jednoznačně určena dvěma body, na obrázku je přímka p určená body A a B. Každý vektor, který je rovnoběžný s vektorem \overrightarrow{AB} se nazývá směrový vektor přímky p. Kterýkoliv z vektorů na obrázku je směrový vektor přímky p. K tomu, abychom určili konkrétní přímku ještě potřebujeme znát jeden bod na přímce (přímka p na obrázku je určena bodem A a kterýmkoliv z vektorů \vec{u}, \vec{v}, \vec{w}).
Parametrické rovnice přímky
Přímka určená bodem A=[a_1;a_2] a vektorem \vec{u}=(u_1;u_2) má parametrické rovnice tvaru: \begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array} Zkráceně můžeme vyjádřit p:X=A+t\vec{u}, číslo t nazýváme parametr.
Jak souvisí hodnota parametru t s polohou bodu na přímce
- Přímka p je určená bodem A a vektorem \vec{u}=\overrightarrow{AB}, tedy p:X=A+t\vec{u}
- Pro hodnotu t=0 dostaneme: X=A+t\vec{u}=A+0\cdot \vec{u} … bod A
- Pro hodnotu t=1 dostaneme: X=A+t\vec{u}=A+1\cdot \vec {u} … bod B
- Pro hodnotu t=2 dostaneme: X=A+t\vec{u}=A+2\cdot \vec {u} … bod C
- Pro hodnotu t=\frac{1}{2} dostaneme: X=A+t\vec{u}=A+\frac{1}{2}\cdot \vec{u} … bod D (střed úsečky AB)
- Pro hodnotu t=-1 dostaneme: X=A+t\vec{u}=A-1\cdot \vec{u} … bod E
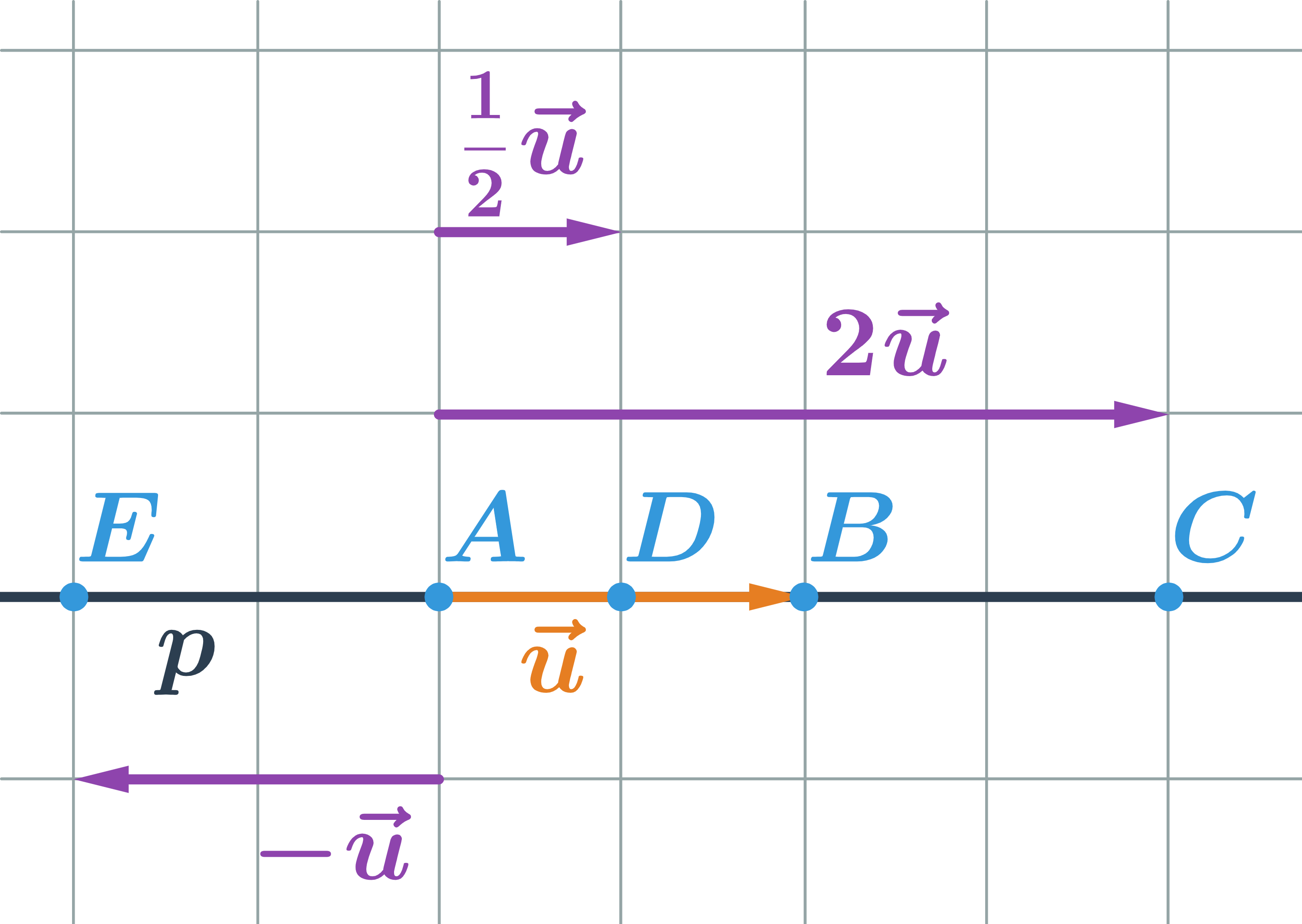
- Každá hodnota parametru určuje jeden bod na přímce, pro určení celé přímky tedy potřebujeme všechna reálná čísla, proto píšeme t\in\mathbb{R}.
- Body, které leží na úsečce AB (tedy body ležící mezi body A a B), vyjádříme parametricky, pokud do rovnice X=A+t\vec{u} dosadíme hodnoty parametru t splňující 0\leq t\leq1.
Obecná rovnice přímky
Každý vektor kolmý k přímce p se nazývá normálový vektor přímky p. Obecná rovnice přímky je rovnice ve tvaru: ax+by+c=0, kde konstanty a a b jsou souřadnice normálového vektoru a c reálné číslo.
Souřadnice směrového a normálového vektoru přímky p
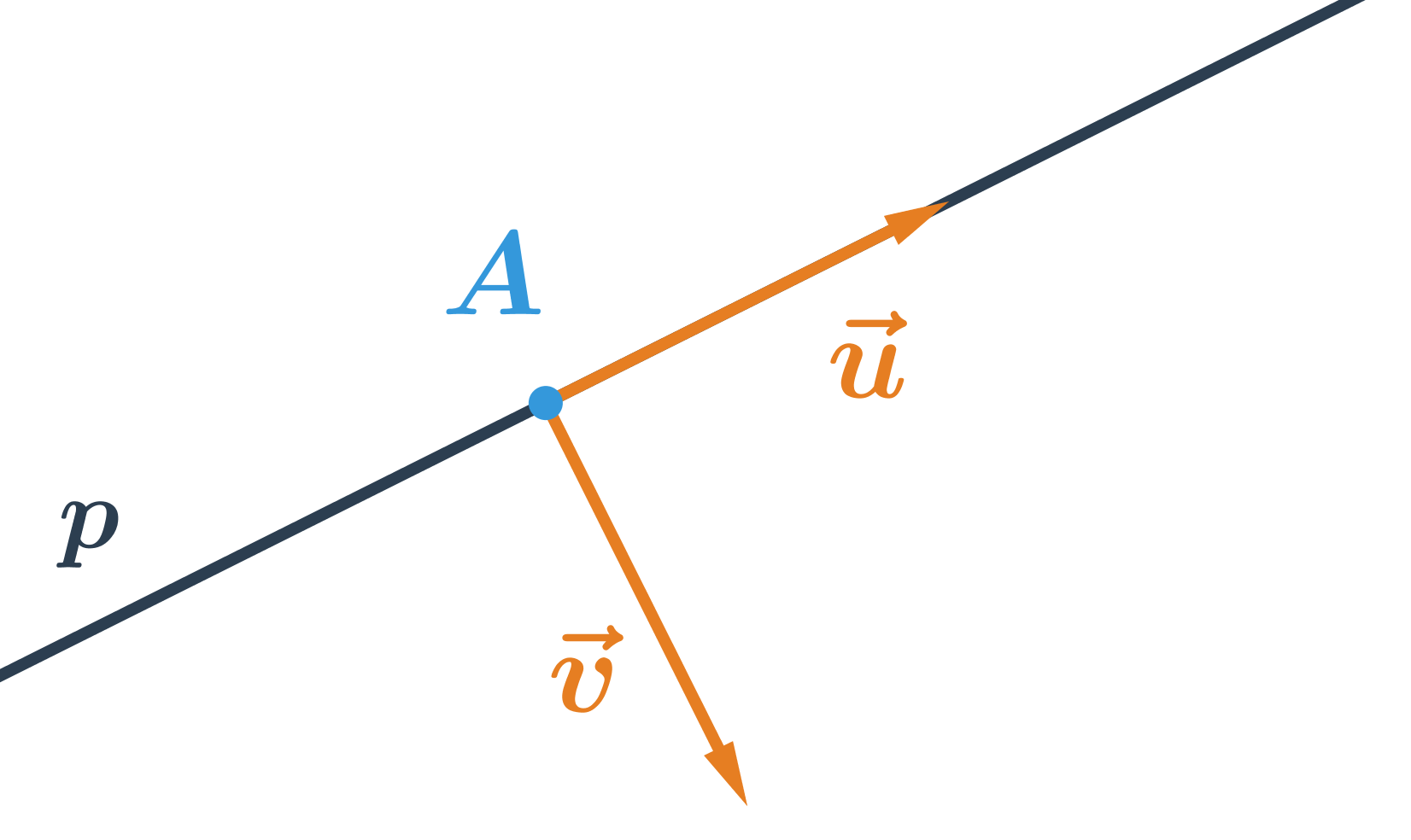
- Pro přímku danou obecnou rovnicí ax+by+c=0:
- \vec{v} je normálový vektor přímky p, jeho souřadnice jsou: \vec{v}=(a;b)
- \vec{u} je směrový vektor přímky p, protože je to vektor kolmý k vektoru \vec{v}=(a;b), jeho souřadnice jsou: \vec{u}=(-b;a)
- Pro přímku danou parametricky: \begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array}
- \vec{u} je směrový vektor přímky p, jeho souřadnice jsou: \vec{u}=(u_1;u_2)
- \vec{v} je normálový vektor přímky p, protože je to vektor kolmý k vektoru \vec{u}=(u_1;u_2), jeho souřadnice jsou: \vec{v}=(-u_2;u_1)
Obecná rovnice přímky rovnoběžné s osou x
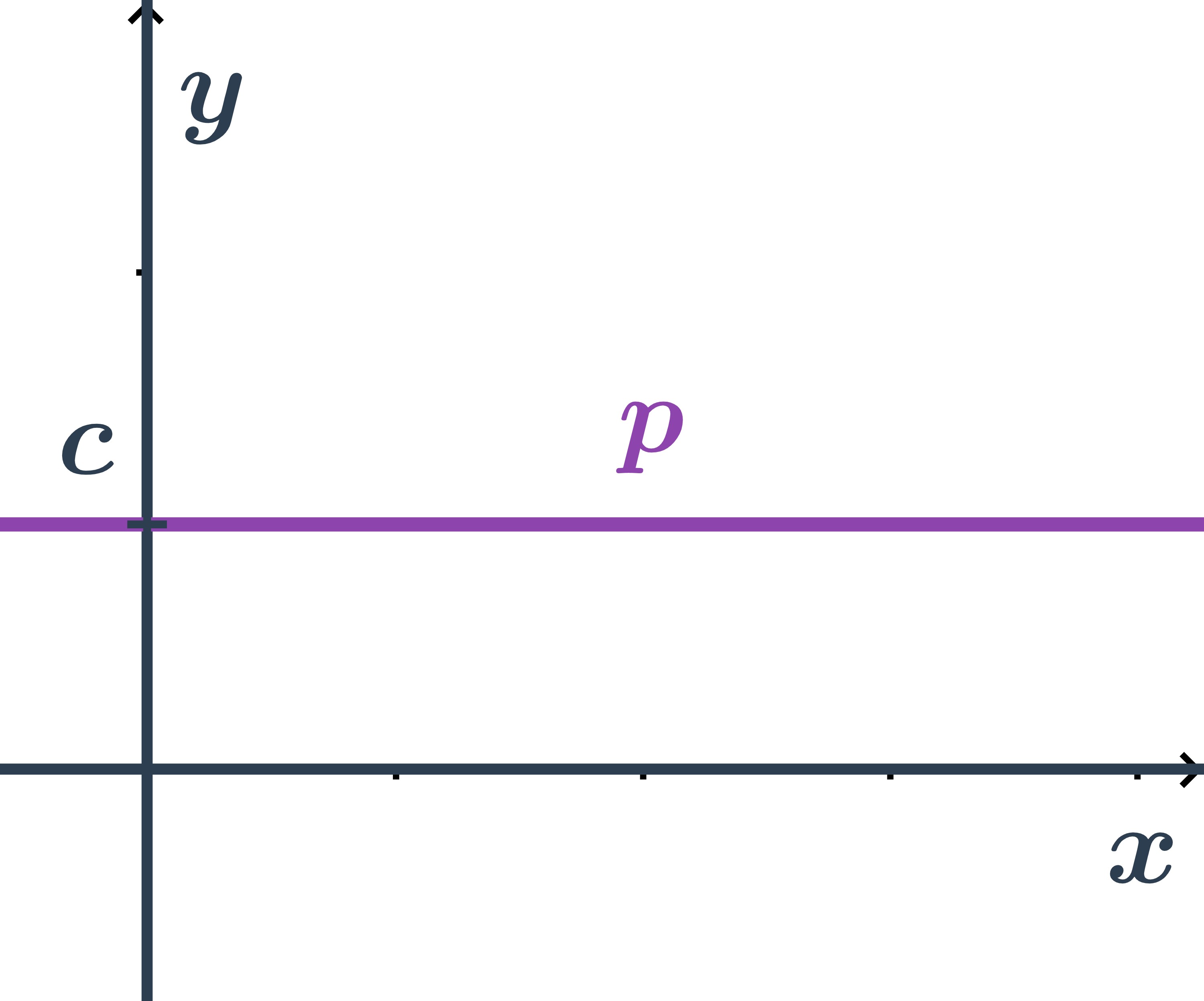
- Pro všechny body ležící na přímce je druhá souřadnice stejná a to: y=c
- Tedy přímka má obecnou rovnici: y-c=0
Obecná rovnice přímky rovnoběžné s osou y
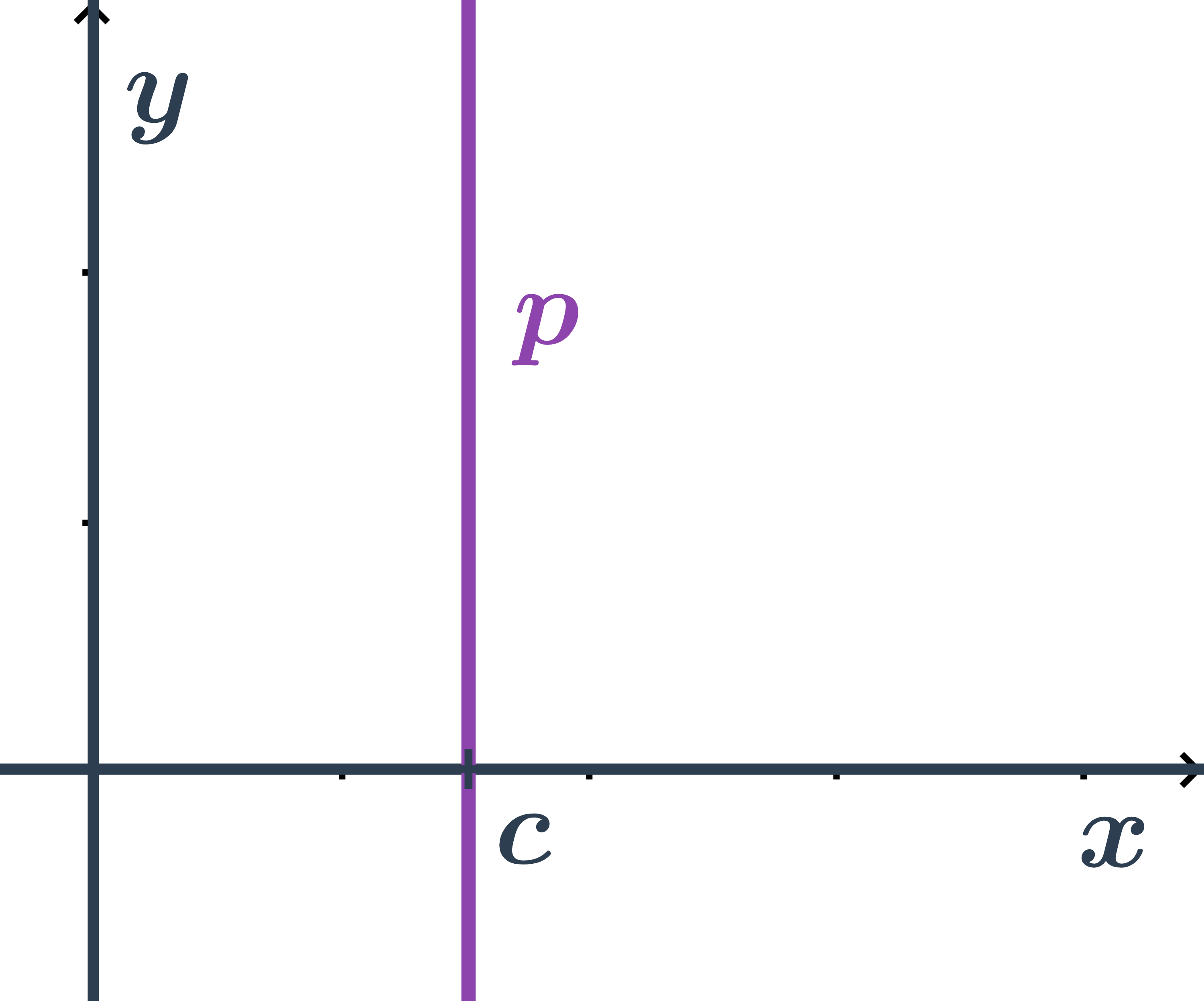
- Pro všechny body ležící na přímce je první souřadnice stejná a to: x=c
- Tedy přímka má obecnou rovnici: x-c=0
Bod a přímka
Bod M=[m_1;m_2] leží na přímce, jestliže jeho souřadnice vyhovují rovnici přímky. Pokud je přímka daná obecnou rovnicí ax+by+c=0, pro souřadnice bodu, který leží na přímce platí: a\cdot m_1+b\cdot m_2+c=0 Pokud je přímka daná parametricky, po dosazení souřadnic bodu vychází z obou rovnic stejná hodnota parametru t. (Více o vzájemné poloze bodu a přímky.)
Obecná rovnice přímky, která prochází počátkem
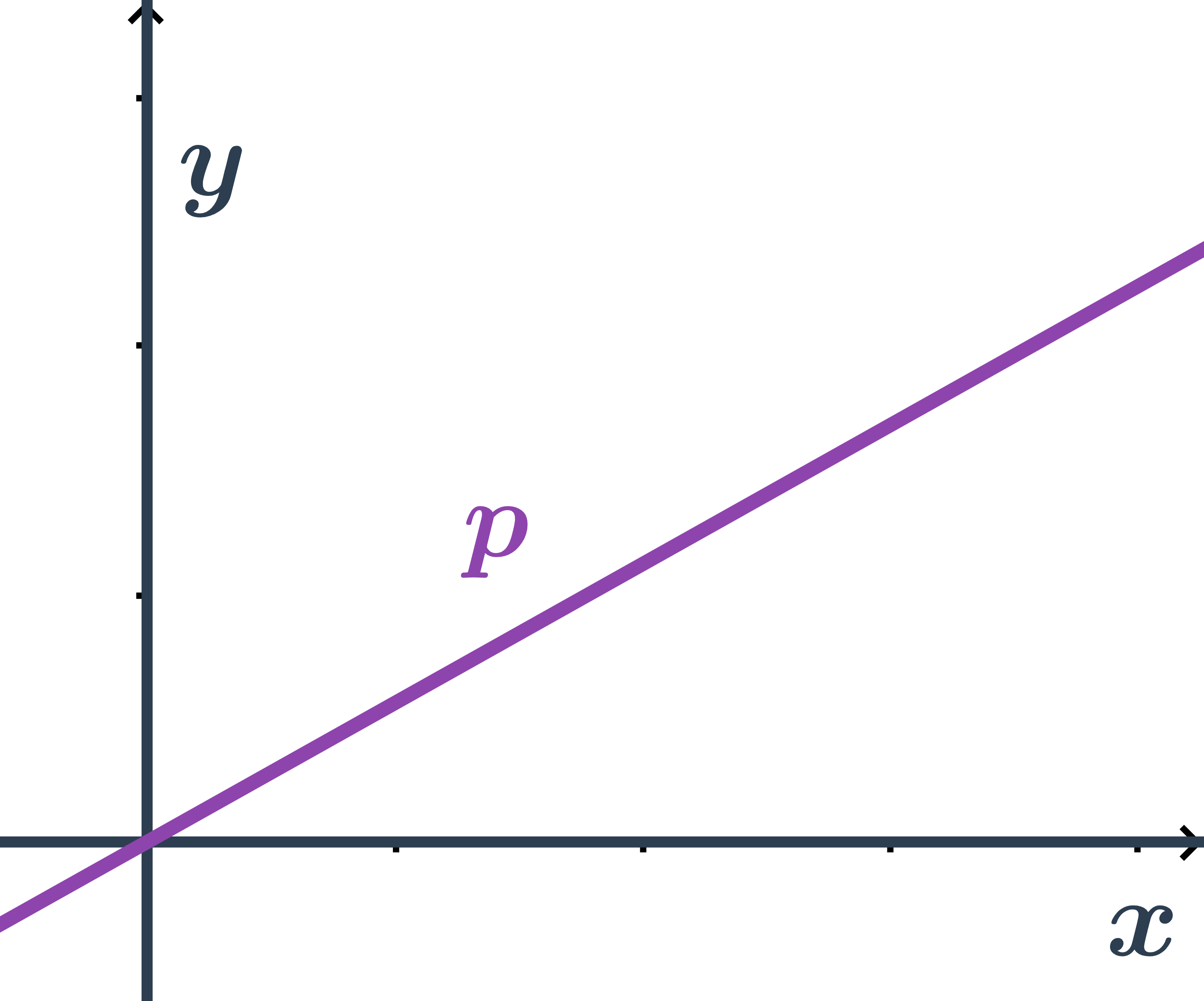
- Přímka prochází bodem O=[0;0], tedy souřadnice počátku splňují její obecnou rovnici ax+by+c=0.
- Dosadíme souřadnice bodu O a zkusíme zjistit nějaké informace o konstantách a,b,c.
- a\cdot0+b\cdot0+c=0\Leftrightarrow c=0
- Proto přímka, která prochází počátkem má obecnou rovnici ax+by=0.
Dvě přímky
Přímky rovnoběžné mají stejný směr, tedy jejich směrové vektory jsou kolineární. Normálové vektory dvou rovnoběžných přímek jsou také kolineární. Ve speciálním případě mohou být přímky totožné.
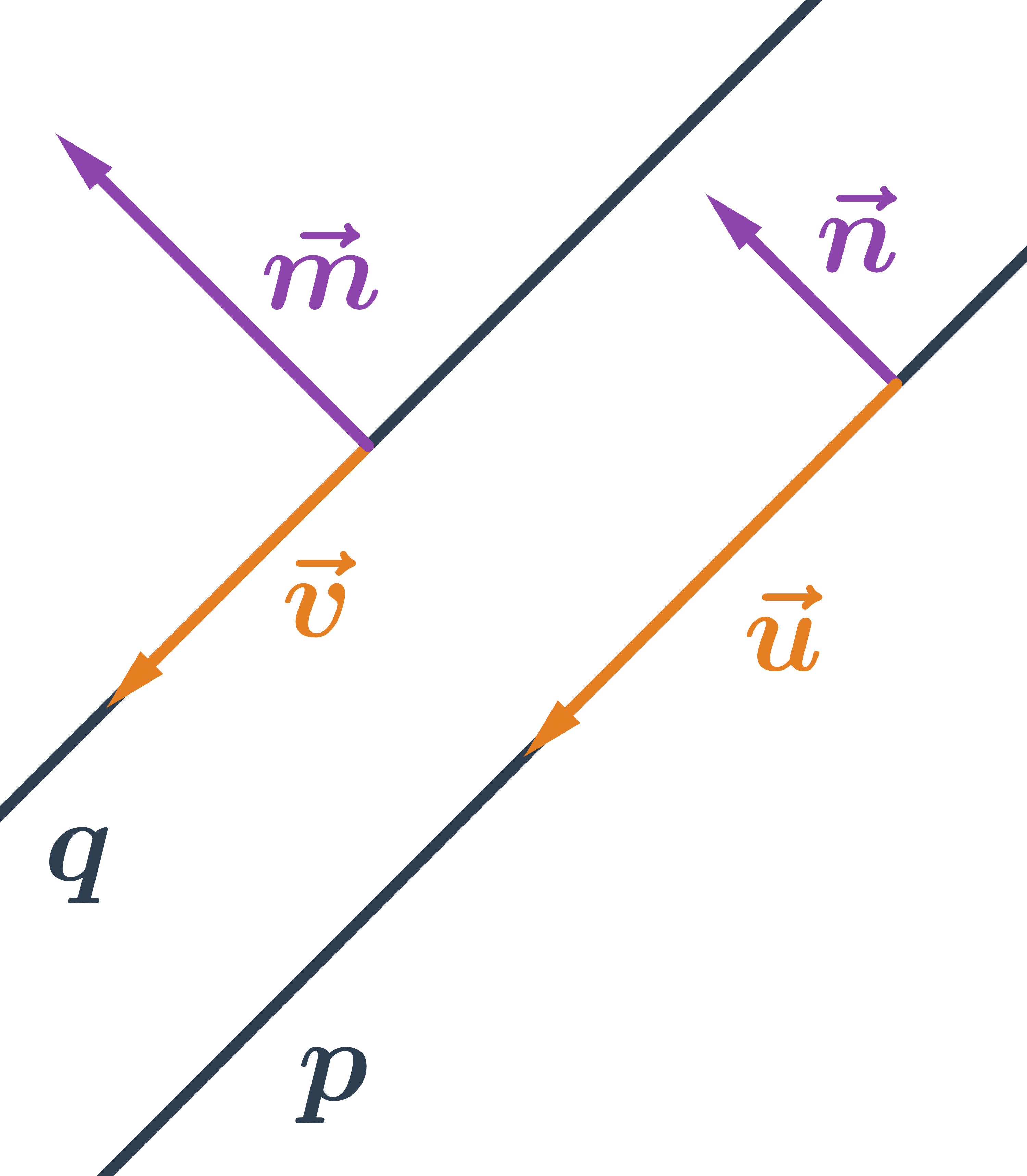
Přímky různoběžné mají jeden společný bod, tento bod musí splňovat rovnice obou přímek. Jejich směrové vektory nejsou kolineární, normálové vektory také nejsou kolineární.
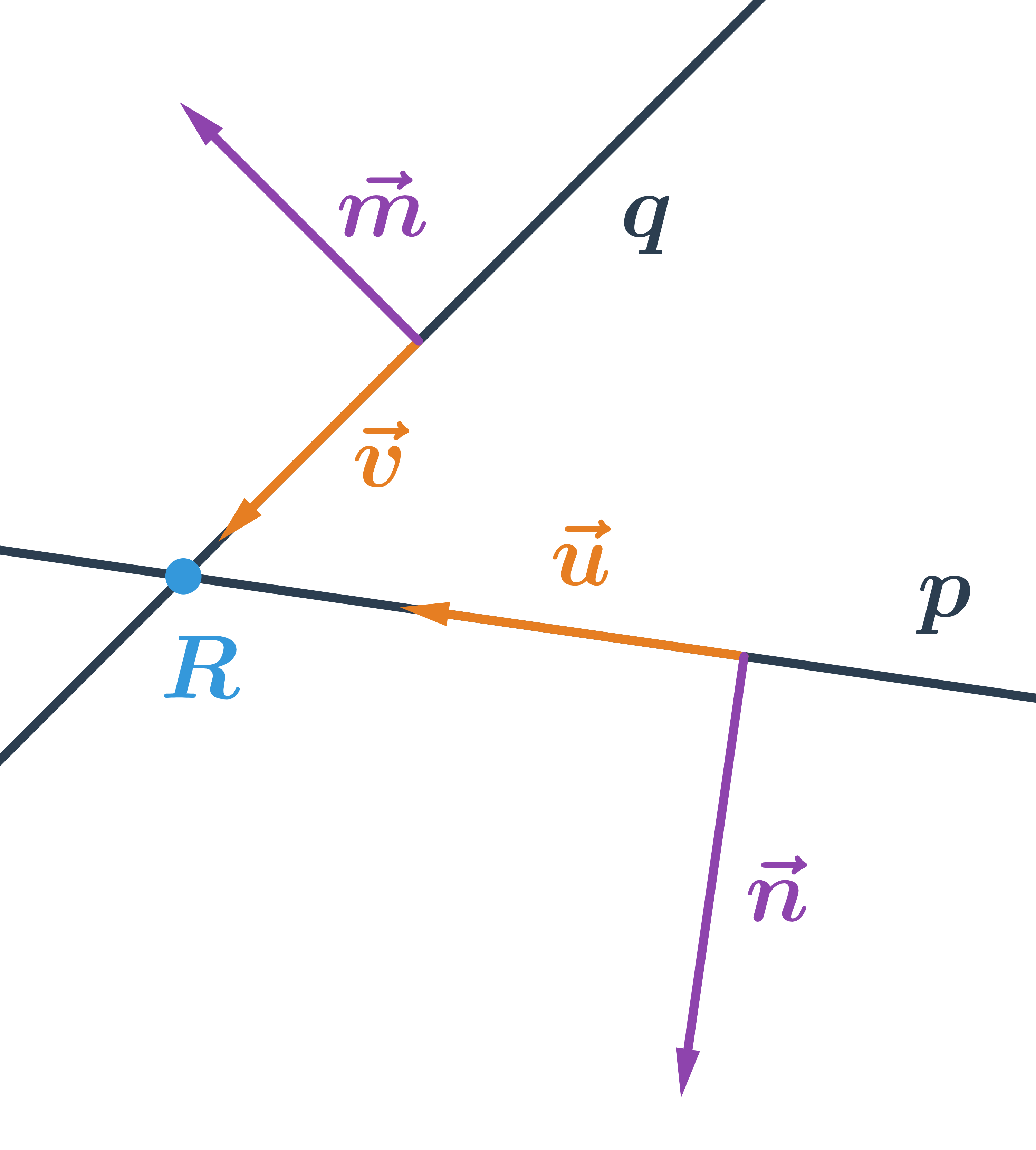
Více o vzájemné poloze dvou přímek.
Přímka v prostoru
Přímku v prostoru nelze vyjádřit obecnou rovnicí. Parametrickou rovnici přímky v prostoru určíme obdobně jako v rovině na základě znalosti souřadnic směrového vektoru a jednoho bodu na přímce.
NahoruUrčení přímky
Přímka je obvykle určena bodem a vektorem, případně dvěma body.
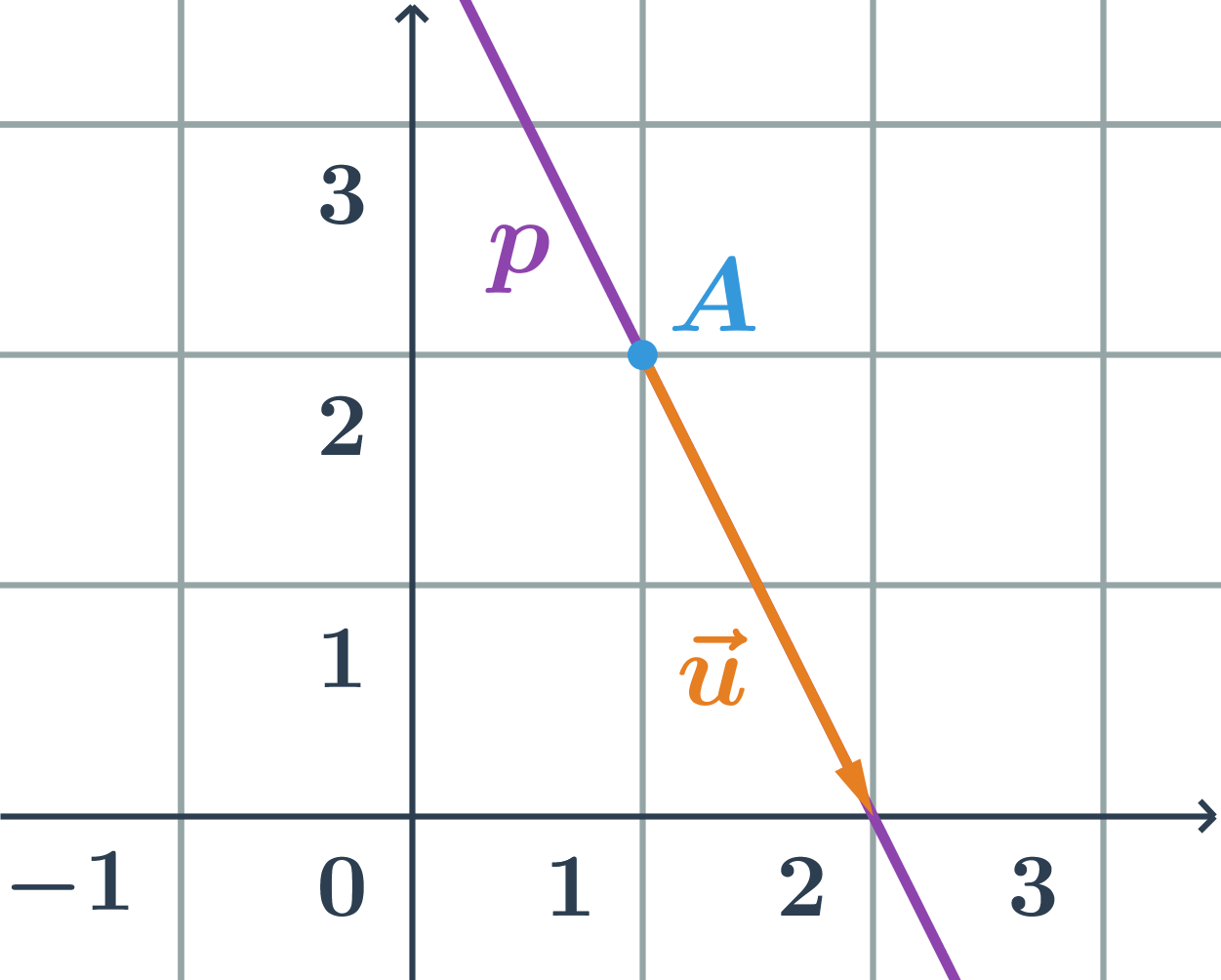
Přímka p na obrázku je určena například:
- bodem A=[1;2], který na ní leží a směrovým vektorem \vec{u}=(1;-2)
- nebo dvěma různými body [1;2] a [2;0], které na ní leží
Parametrické rovnice přímky v rovině
Přímka určená bodem A=[a_1;a_2] a směrovým vektorem \vec{u}=(u_1;u_2) má parametrické rovnice tvaru:
\begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array}
Zkráceně můžeme vyjádřit p:X=A+t\vec{u}, číslo t nazýváme parametr. Pokud známe dva body A, B ležící na přímce, směrový vektor je například \vec{u}=\overrightarrow{AB}.
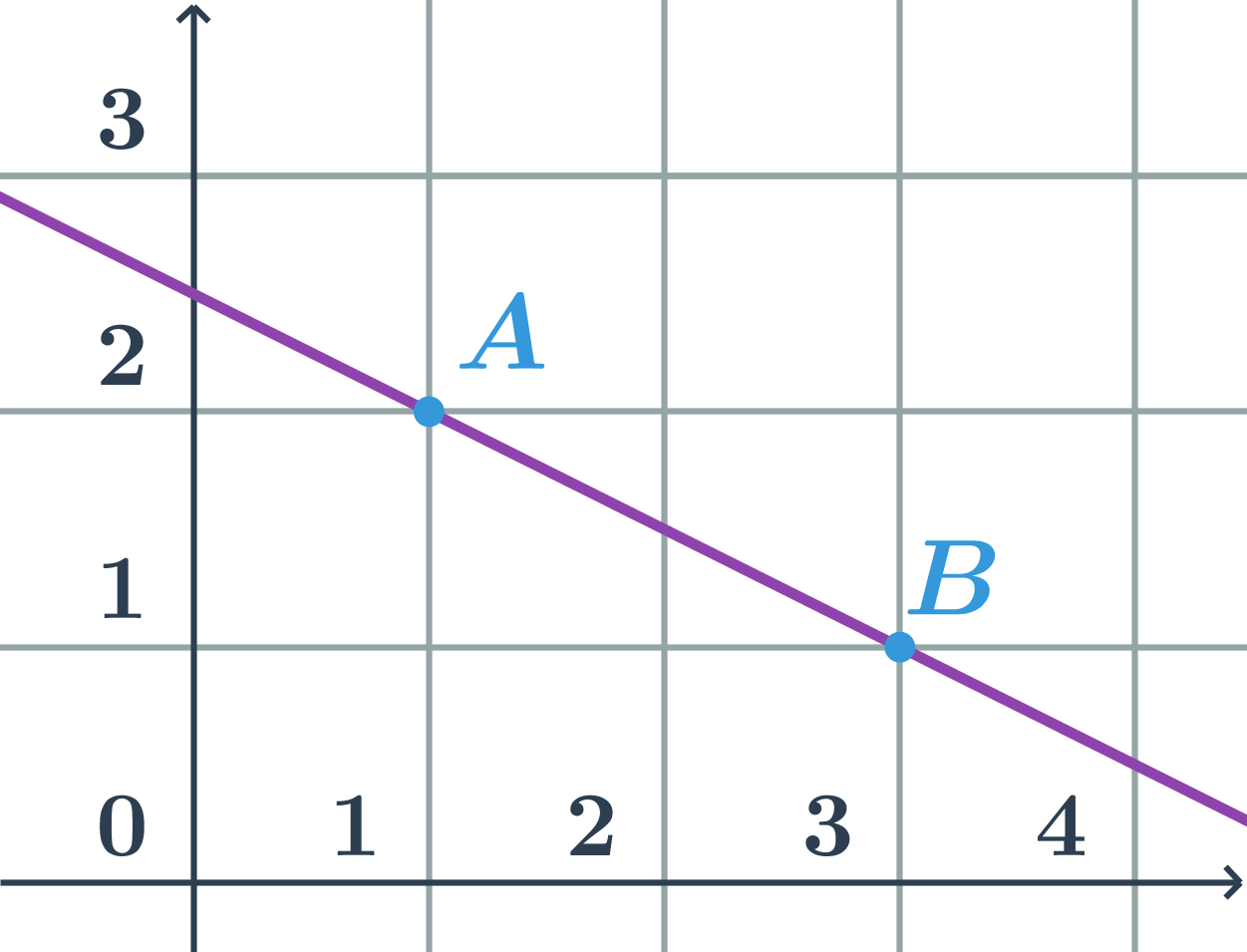
Parametrické rovnice přímky p určené body A=[1;2] a B=[3;1]
- přímka p je určená bodem A a směrovým vektorem \vec{u}=\overrightarrow{AB}=B-A=(2;-1)
- parametrické rovnice přímky p: \begin{array}{rrl}x&=&1+2t\\y&=&2-t\\&&t\in\mathbb{R}\end{array}
Různé parametrické rovnice přímky na obrázku
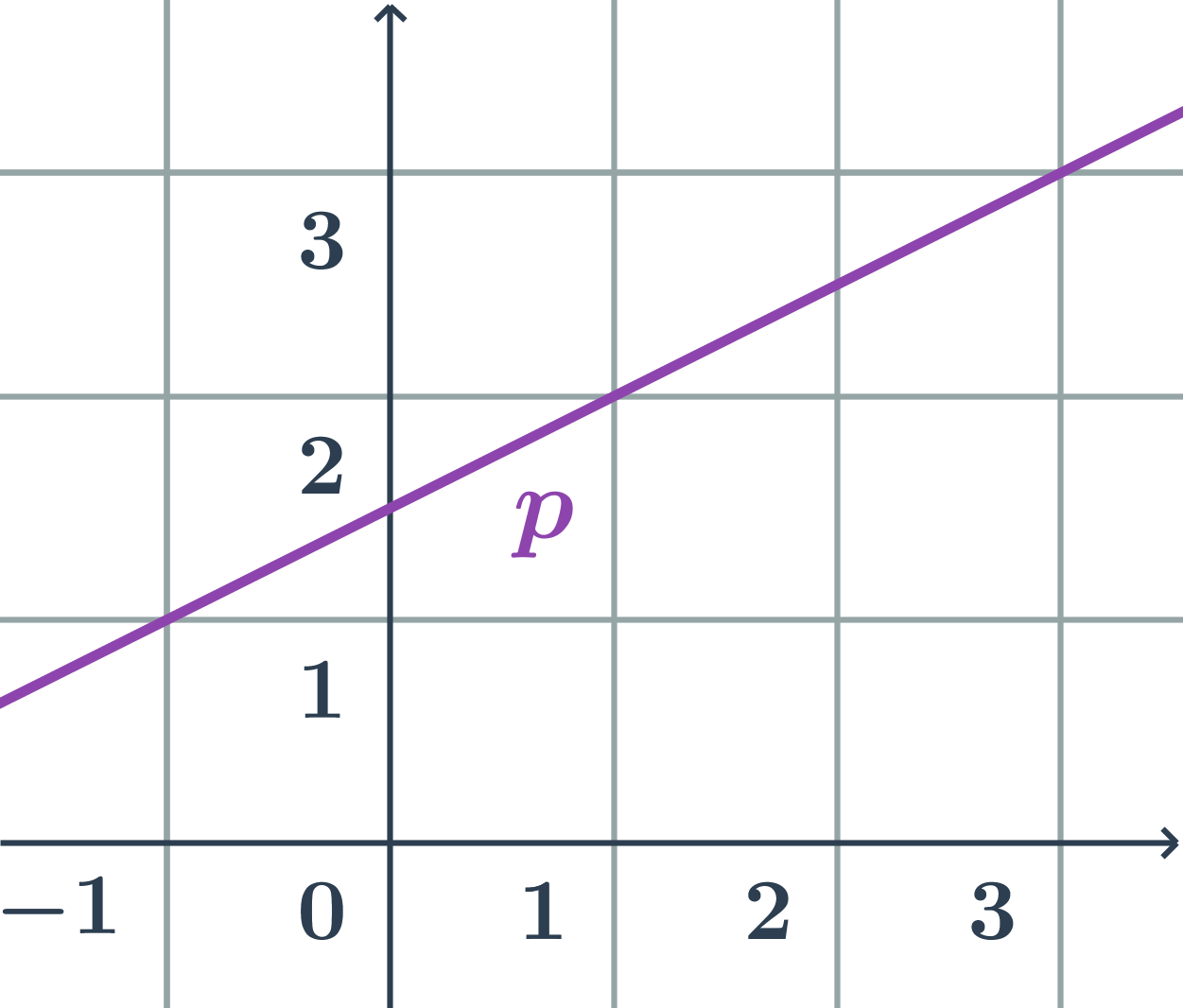
Určíme souřadnice směrového vektoru a jednoho bodu na přímce:
- například: \vec{u}=(2;1), A=[1;2]
- parametrické rovnice přímky p: \begin{array}{rrl}x&=&1+2t\\y&=&2+t\\&&t\in\mathbb{R}\end{array}
Další možnost parametrického vyjádření:
- \vec{v}=(-4;-2), B=[3;3]
- parametrické rovnice přímky p: \begin{array}{rrl}x&=&3-4t\\y&=&3-2t\\&&t\in\mathbb{R}\end{array}
Pro určení parametrických rovnic můžeme vybrat kterýkoliv bod ležící na přímce a jakýkoliv zápis souřadnic směrového vektoru, možností jak parametricky vyjádřit danou přímku je tedy nekonečně mnoho.
Obecná rovnice přímky v rovině
Obecná rovnice přímky v rovině má tvar: ax+by+c=0, kde konstanty a a b jsou souřadnice normálového vektoru a c reálné číslo. Normálový vektor \vec{n}=(a;b) je vektor kolmý k dané přímce, tedy i kolmý ke směrovému vektoru přímky.
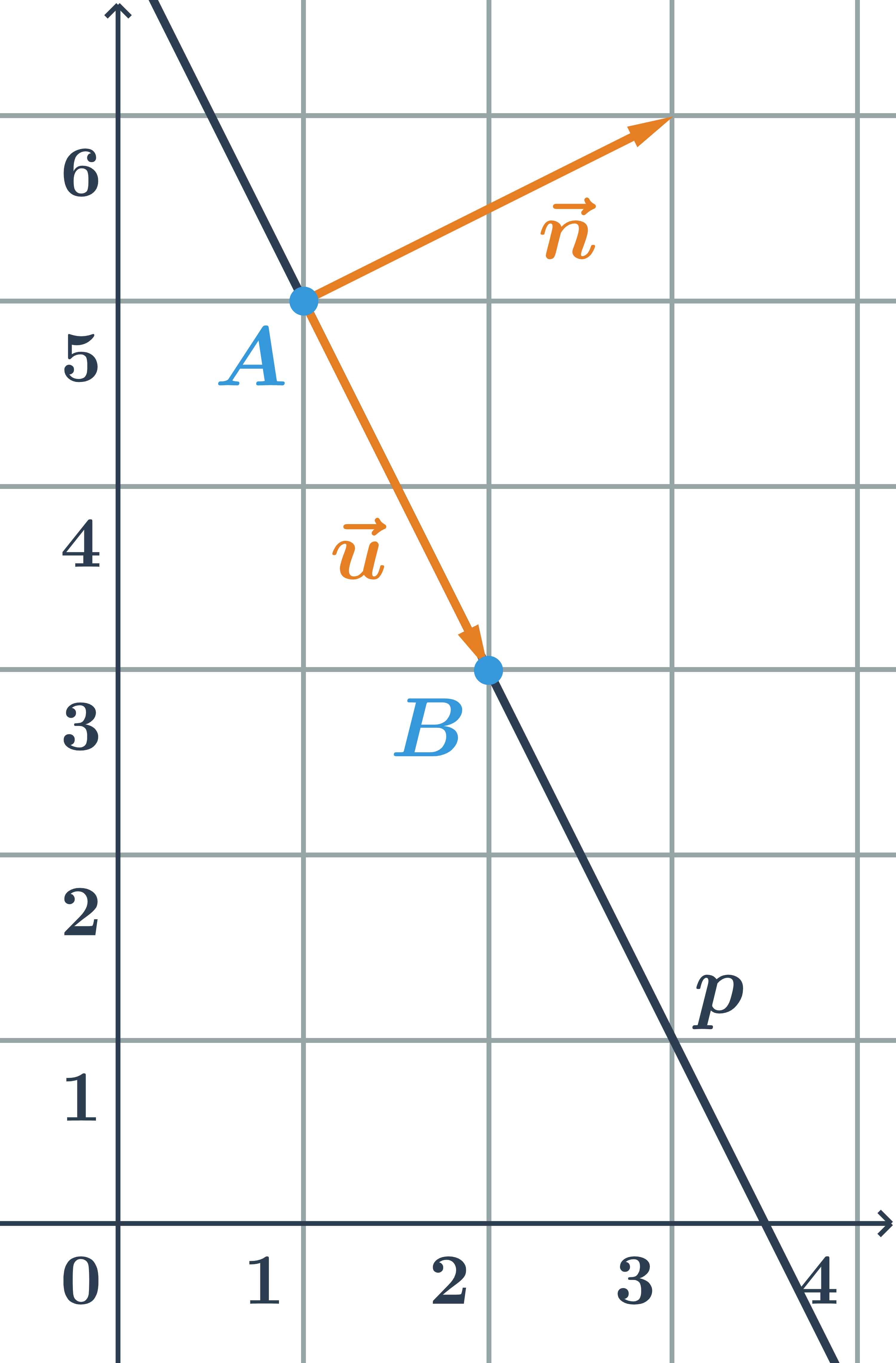
Obecná rovnice přímky p určené body A=[1;5] a B=[2;3]
- Přímka p je určená bodem A a směrovým vektorem \vec{u}=\overrightarrow{AB}=B-A=(1;-2).
- Normálový vektor je kolmý k vektoru \vec{u}=(1;-2), tedy například vektor \vec{n}=(2;1).
- Souřadnice normálového vektoru jsou konstanty a a b v obecné rovnici přímky. Obecná rovnice má tvar: 2x+y+c=0
- Konstantu c dopočítáme dosazením souřadnic bodu A=[1;5] :
- 2\cdot1+5+c=0\Rightarrow c=-7
- Obecná rovnice přímky p je: 2x+y-7=0
Obecná rovnice přímky dané parametricky
Určete obecnou rovnici přímky p, která je dána následující parametrickou soustavou rovnic: \begin{array}{rrl}x&=&1+2t\\y&=&4+6t\\&&t\in\mathbb{R}\end{array}
- Přímka p je určená bodem A=[1;4] a směrovým vektorem \vec{u}=(2;6).
- Souřadnice směrového vektoru můžeme upravit na tvar: \vec{u}=(1;3).
- Normálový vektor je kolmý k vektoru \vec{u}=(1;3), tedy například vektor \vec{n}=(3;-1).
- Souřadnice normálového vektoru jsou konstanty a a b v obecné rovnici přímky. Obecná rovnice má tvar: 3x-y+c=0
- Konstantu c dopočítáme dosazením souřadnic bodu A=[1;4] :
- 3\cdot1-4+c=0\Rightarrow c=1
- Obecná rovnice přímky p je: 3x-y+1=0
Parametrické vyjádření přímky dané obecnou rovnicí
Určete parametrické vyjádření přímky p, která má obecnou rovnici: 3x-2y+4=0.
- Přímka p má normálový vektor \vec{n}=(3;-2).
- Směrový vektor je kolmý k vektoru \vec{n}=(3;-2), tedy například vektor \vec{u}=(2;3).
- Určíme jeden bod na přímce p : jednu souřadnici můžeme zvolit, například x=0, druhou souřadnici dopočítáme: 3\cdot0-2y+4=0\Rightarrow y=2
- Z obecné rovnice jsme tedy zjistili, že na přímce leží bod A=[0;2].
- Parametrické vyjádření přímky p je: \begin{array}{rrl}x&=&0+2t\\y&=&2+3t\\&&t\in\mathbb{R}\end{array}
Směrnicový tvar rovnice přímky
Každou přímku p, která není rovnoběžná s osou y, můžeme vyjádřit ve tvaru: y=kx+q, kde k,q\in\mathbb{R}.
Tento tvar se nazývá směrnicový tvar rovnice přímky.
Konstanta k se nazývá směrnice a její hodnota je tangens úhlu, který svírá přímka p s kladnou částí osy x, tedy: k=\tan \varphi.
Konstanta q určuje průsečík přímky p s osou y, souřadnice průsečíku jsou: P=[0;q]. Pro přímku, která prochází počátkem, je q=0, tedy směrnicový tvar její rovnice je: y=kx.
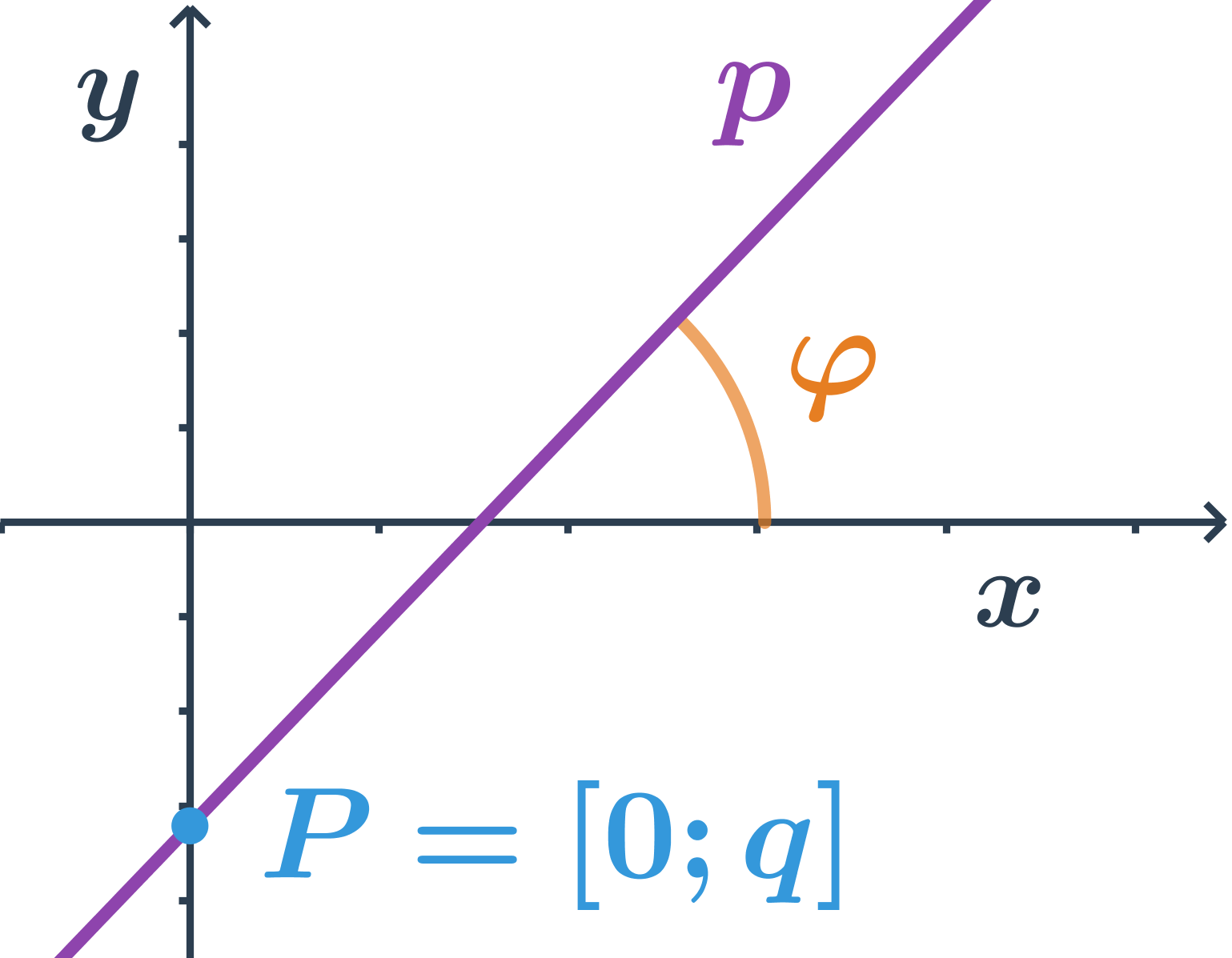
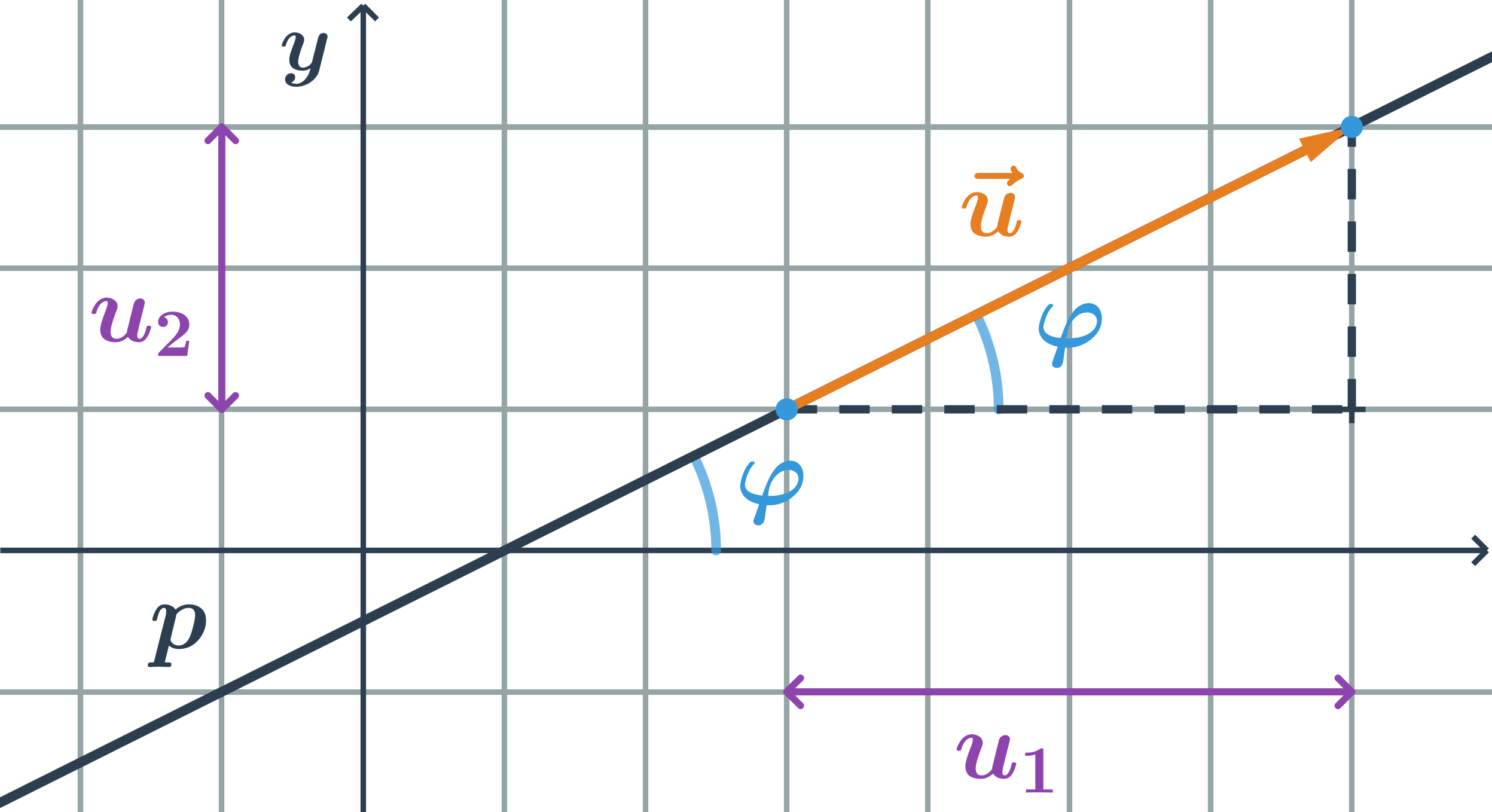
Směrnice přímky, která má směrový vektor \vec{u}=(u_1;u_2), je podíl souřadnic směrového vektoru:
k=\tan \varphi=\frac{u_2}{u_1}
Různé hodnoty směrnice
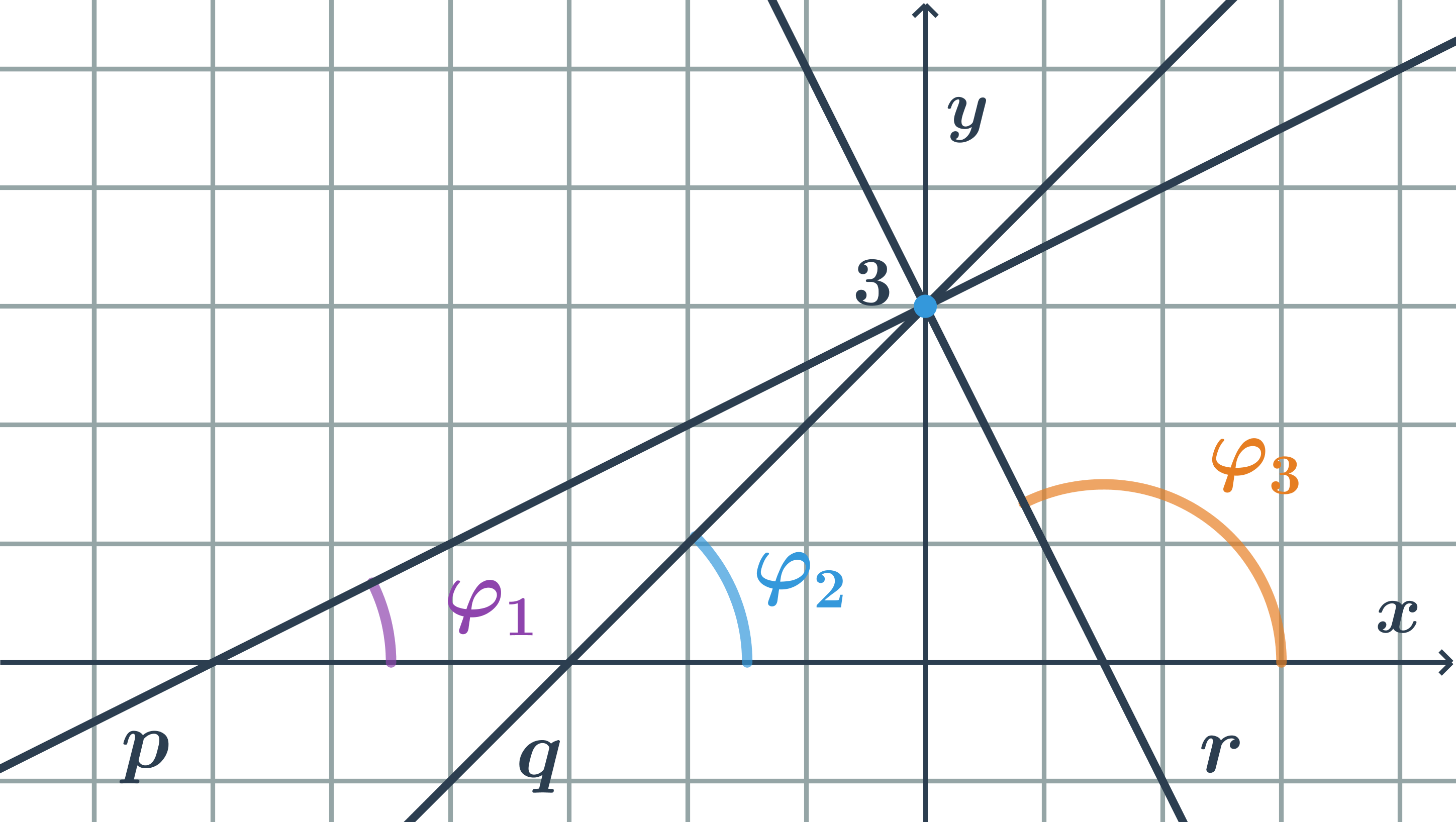
- Směrnice přímky p: k_1=\tan \varphi_1=\frac{1}{2}
- Směrnice přímky q: k_2=\tan \varphi_2=\frac{1}{1}=1
- Směrnice přímky r: k_3=\tan \varphi_3=\frac{2}{1}=2
- Čím větší odchylka od kladné části osy x, tím větší hodnota směrnice k.
- Přímka rovnoběžná s osou x svírá s kladnou částí osy x úhel 0^\circ a tedy její směrnice je \tan 0^\circ=0.
- Přímka rovnoběžná s osou y svírá s kladnou částí osy x úhel 90^\circ a pro tuto hodnotu funkce tangens není definována, proto nemůžeme určit směrnici.
Směrnicový tvar přímky z obrázku
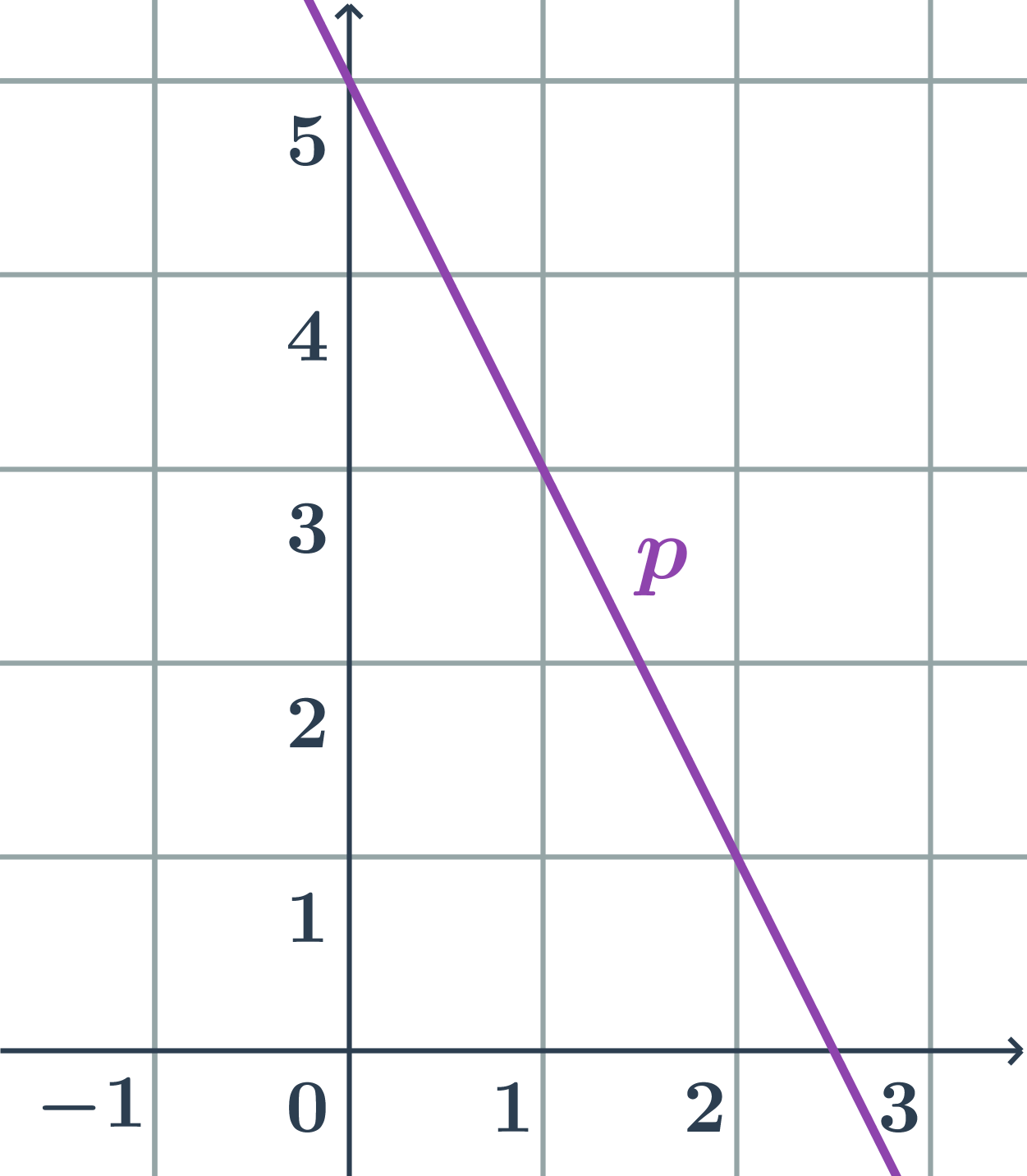
Hledáme směrnicový tvar rovnice přímky: y=kx+q.
- Pro nalezení konstant k a q určíme směrový vektor přímky p a průsečík s osou y.
- směrový vektor přímky: \vec{u}=(1;-2)
- směrnice: k=\tan \varphi=\frac{u_2}{u_1}=\frac{-2}{1}=-2
- průsečík přímky s osou y: P=[0;5]
- konstanta q=y_P=5
- přímka na obrázku má směrnicový tvar y=-2x+5
Dvě přímky
Dvě rovnoběžné přímky svírají s kladnou částí osy x stejný úhel, mají tedy stejnou směrnici.
Pro dvě k sobě kolmé přímky platí:
- přímka p má směrový vektor \vec{u}=(u_1;u_2) a tedy směrnici: k=\frac{u_2}{u_1}
- každá přímka k ní kolmá má směrový vektor (-u_2;u_1) a tedy směrnici: \frac{u_1}{-u_2}=-\frac{1}{k}
Vzájemná poloha přímek v rovině
Vzájemnou polohu dvou přímek můžeme snadno určit, pokud známe souřadnice jejich směrových, případně normálových vektorů. Přímky rovnoběžné mají stejný směr, tedy jejich směrové vektory jsou kolineární. Normálové vektory dvou rovnoběžných přímek jsou také kolineární. Ve speciálním případě mohou být přímky totožné. Přímky různoběžné mají jeden společný bod, tento bod musí splňovat rovnice obou přímek. Jejich směrové vektory nejsou kolineární, normálové vektory také nejsou kolineární.
Rovnoběžky zadané parametrickými rovnicemi
Určete vzájemnou polohu dvou přímek p, q zadaných parametricky:
p: \begin{array}{rrl}x&=&-3+3t\\y&=&\hspace{0.25cm}2+t\\&&\hspace{0.25cm}t\in\mathbb{R}\end{array} \hspace{0.5cm}q: \begin{array}{rrl}x&=&1-3s\\y&=&2-s\\&&s\in\mathbb{R}\end{array}
- směrový vektor přímky p:\hspace{0.25cm}\vec{u}=(3;1)
- směrový vektor přímky q:\hspace{0.25cm}\vec{v}=(-3;-1)
- Přímky p a q jsou rovnoběžné, protože jejich směrové vektory jsou kolineární.
- Ověříme, že přímky nejsou totožné. Stačí určit, zda bod, který leží na jedné přímce neleží na přímce druhé.
- Na přímce p leží například bod A=[-3;2].
- Ověříme, že tento bod neleží na přímce q dosazením souřadnic bodu A do rovnic přímky q: \begin{array}{rrl}-3&=&1-3s \Rightarrow s=\frac{4}{3}\\2&=&2-\hspace{0.15cm}s\Rightarrow s=0\end{array}
- Vyšly různé hodnoty parametru s, takže bod A neleží na q \Rightarrow přímky nejsou totožné
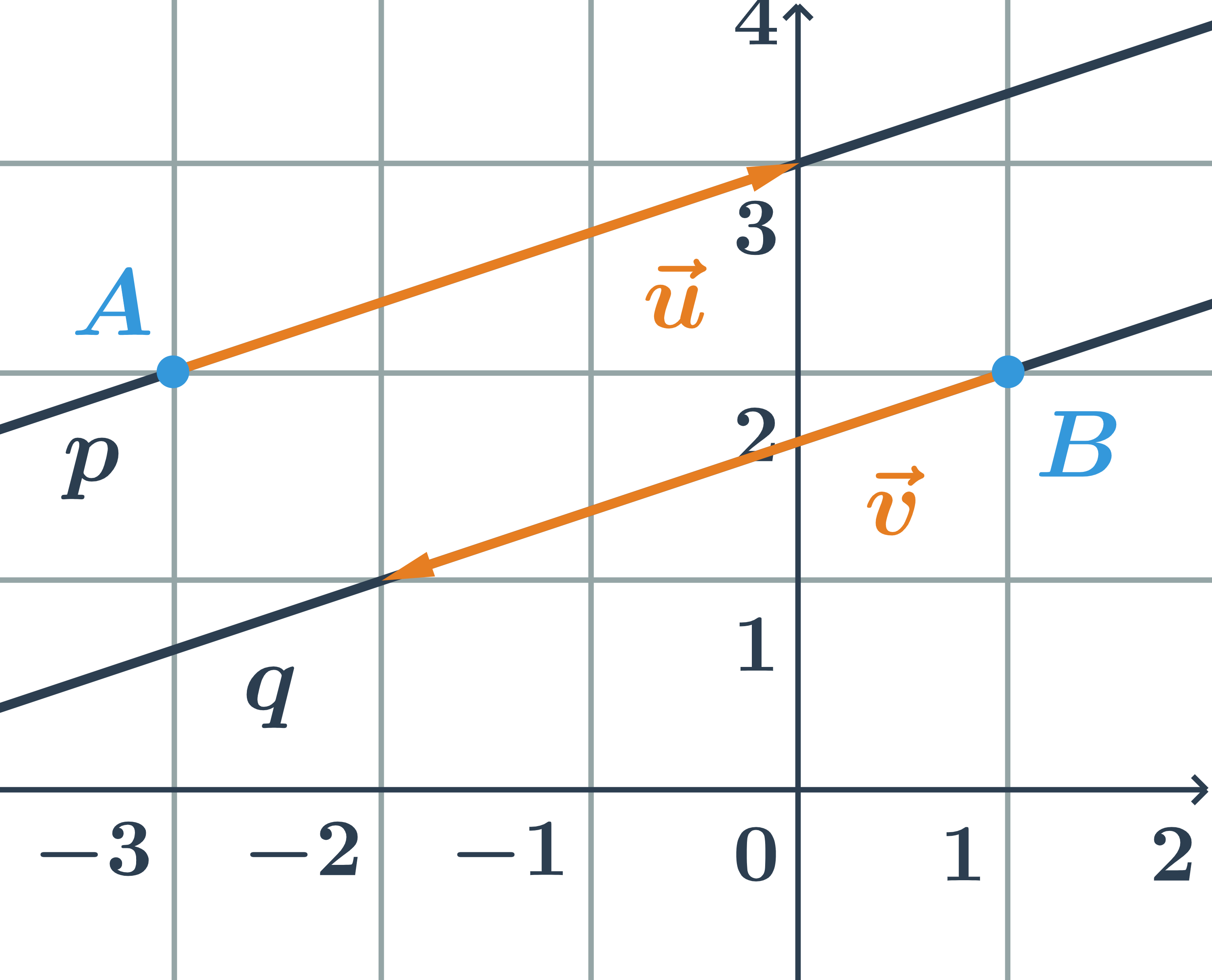
Rovnoběžky zadané obecnými rovnicemi
Určete vzájemnou polohu dvou přímek daných obecnými rovnicemi p: 2x+y-1=0 a q:4x+2y+3=0.
- normálový vektor přímky p:\hspace{0.25cm}\vec{n}=(2;1)
- normálový vektor přímky q:\hspace{0.25cm}\vec{m}=(4;2)
- Přímky p a q jsou rovnoběžné, protože jejich normálové vektory jsou kolineární.
- Ověříme, že přímky nejsou totožné. Stačí určit, zda bod, který leží na jedné přímce neleží na přímce druhé.
- Na přímce p leží například bod A=[0;1].
- Ověříme, zda A leží na p dosazením souřadnic bodu A do rovnice přímky p: 4\cdot0+2\cdot1+3\neq 0
- A nesplňuje rovnici, takže neleží na přímce q \Rightarrow přímky nejsou totožné
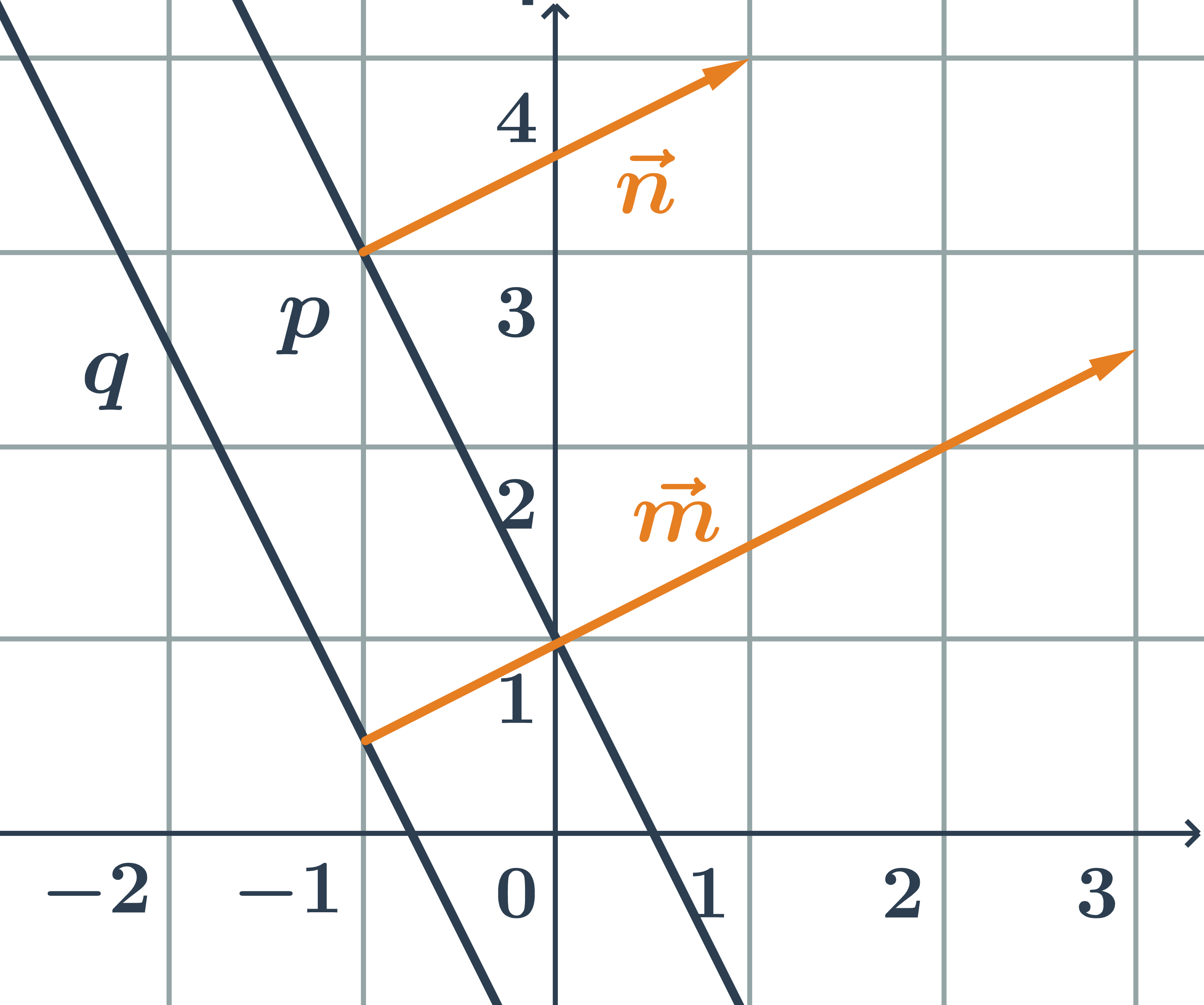
Různoběžky zadané parametrickými rovnicemi
Určete vzájemnou polohu přímek p, q zadaných parametricky:
p: \begin{array}{rrl}x&=&-1+t\\y&=&\hspace{0.25cm}3+2t\\&&\hspace{0.25cm}t\in\mathbb{R}\end{array} \hspace{0.5cm}q: \begin{array}{rrl}x&=&-4+s\\y&=&\hspace{0.25cm}3-s\\&&\hspace{0.25cm}s\in\mathbb{R}\end{array}
- směrový vektor přímky p:\hspace{0.25cm}\vec{u}=(1;2)
- směrový vektor přímky q:\hspace{0.25cm}\vec{v}=(1;-1)
- Přímky p a q jsou různoběžné, protože jejich směrové vektory nejsou kolineární.
Průsečík přímek splňuje rovnice obou přímek, tedy každou z jeho souřadnic lze vyjádřit dvěma způsoby, dostáváme následující soustavu rovnic: \begin{array}{lrr}-1+t&=&-4+s\\\hspace{0.25cm}3+2t&=&3-s\end{array}
- Soustavu můžeme vyřešit sečtením obou rovnic: 2+3t=-1\Rightarrow3+3t=0\Rightarrow t=-1
- Výsledný parametr t dosadíme do parametrických rovnic kterékoliv z přímek a dostaneme souřadnice x,y průsečíku.
Průsečík přímek p a q je bod R=[-2;1].
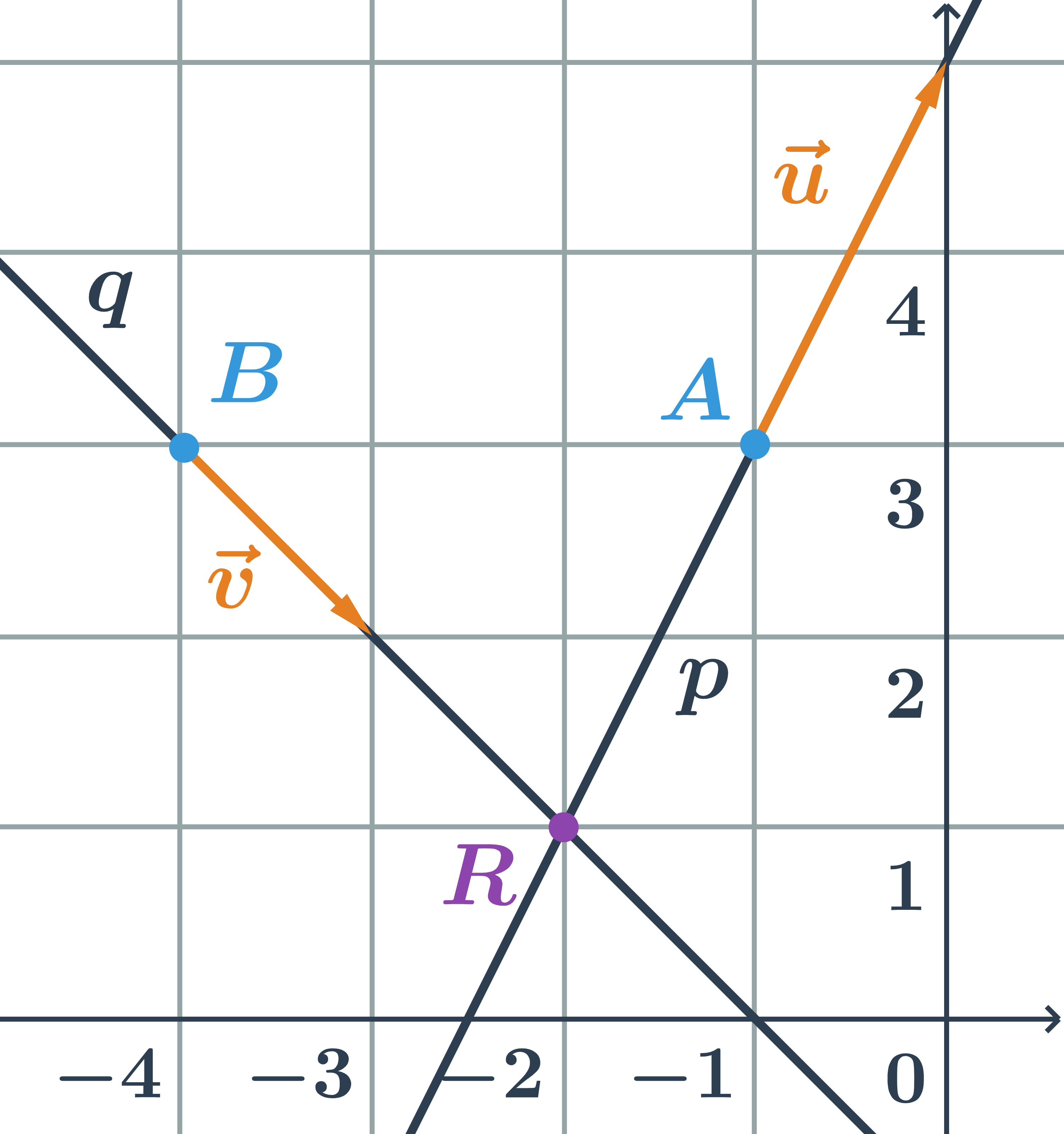
Různoběžky zadané obecnými rovnicemi
Určíme vzájemnou polohu dvou přímek zadaných obecnými rovnicemi p: 2x+y-1=0 a q:x-y+1=0.
- normálový vektor přímky p:\hspace{0.25cm}\vec{n}=(2;1)
- normálový vektor přímky q:\hspace{0.25cm}\vec{m}=(1;-1)
- Přímky p a q jsou různoběžné, protože jejich normálové vektory nejsou kolineární.
- Průsečík přímek splňuje rovnice obou přímek, tedy jeho souřadnice jsou řešením soustavy: \begin{array}{rrr}2x+y-1&=&0\\x-y+1&=&0\end{array}
- Můžeme vyřešit sečtením obou rovnic: 3x=0\Rightarrow x=0
- Průsečík přímek p a q je bod R=[0;1]
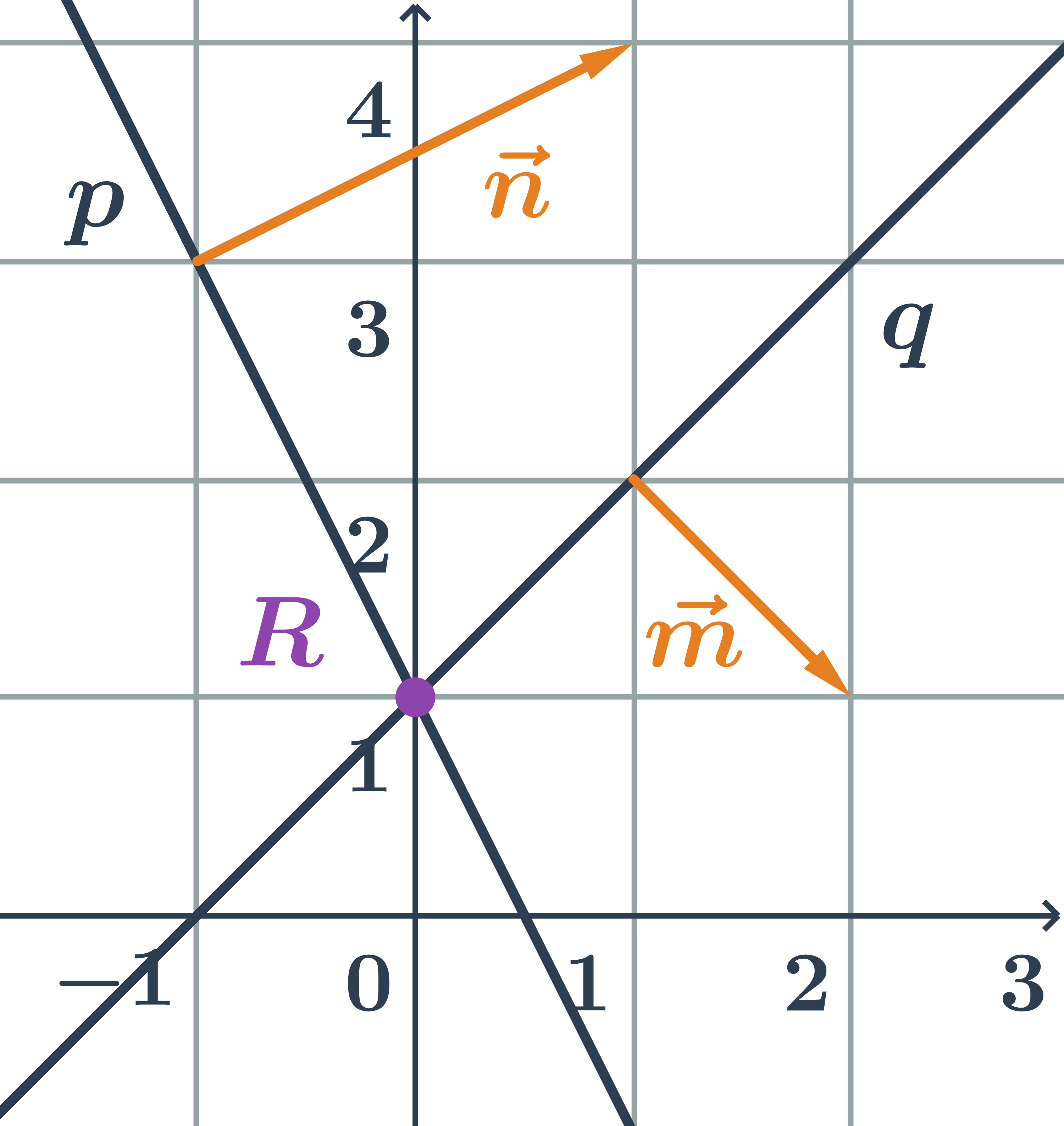
Přímka daná obecnou rovnicí a druhá parametricky – první příklad
Určete vzájemnou polohu přímek p,q zadaných takto:
\hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} \hspace{0.5cm}q: \begin{array}{rrl}x&=&3-2t\\y&=&2-4t\\&&t\in\mathbb{R}\end{array}
- normálový vektor přímky p:\hspace{0.25cm}\vec{n}=(2;-1)
- směrový vektor přímky q:\hspace{0.25cm}\vec{v}=(-2;-4)
- Přímky p a q jsou rovnoběžné, protože jejich směrové vektory jsou kolineární. Proto normálový vektor jedné přímky je kolmý ke směrovému vektoru druhé přímky.
- Ověříme, že přímky nejsou totožné: stačí určit, zda bod, který leží na jedné přímce neleží na přímce druhé.
- Na přímce q leží například bod B=[3;2].
- Na přímce p tento bod neleží, což zjistíme dosazením souřadnic bodu B do rovnice přímky: 2\cdot3-2+3\neq 0
- Bod B nesplňuje rovnici, takže neleží na přímce p \Rightarrow přímky nejsou totožné
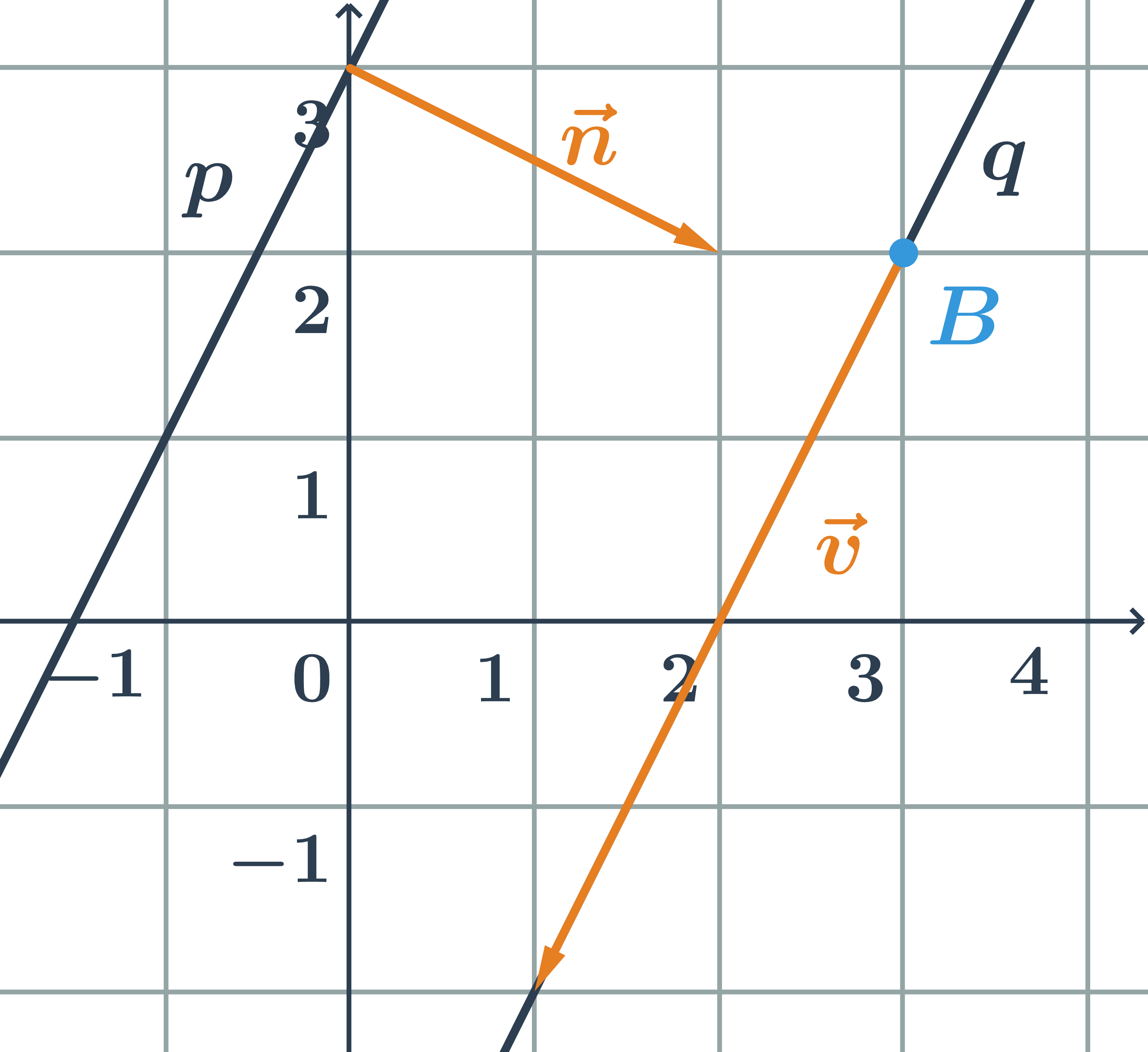
Přímka daná obecnou rovnicí a druhá parametricky – druhý příklad
Určete vzájemnou polohu přímek p,q zadaných:
\hspace{0.25cm}p: x-3y+3=0\hspace{0.25cm} \hspace{0.5cm}q: \begin{array}{rrl}x&=&\hspace{0.28cm}1+t\\y&=&-2+2t\\&&\hspace{0.28cm}t\in\mathbb{R}\end{array}
- normálový vektor přímky p:\hspace{0.25cm}\vec{n}=(1;-3)
- směrový vektor přímky q:\hspace{0.25cm}\vec{v}=(1;2)
- Přímky p a q jsou různoběžné, protože jejich směrové vektory nejsou kolineární. Vyplývá z toho, že normálový vektor jedné přímky není kolmý ke směrovému vektoru druhé přímky.
- Průsečík přímek splňuje rovnice obou přímek, tedy jeho souřadnice najdeme tak, že parametrické vyjádření přímky q dosadíme do obecné rovnice přímky p: \begin{array}{rrl}(1+t)-3(-2+2t)+3&=&0\\1+t+6-6t+3&=&0\\10-5t&=&0\\t&=&2\end{array}
- Průsečík přímek p a q je bod R=[3;2]
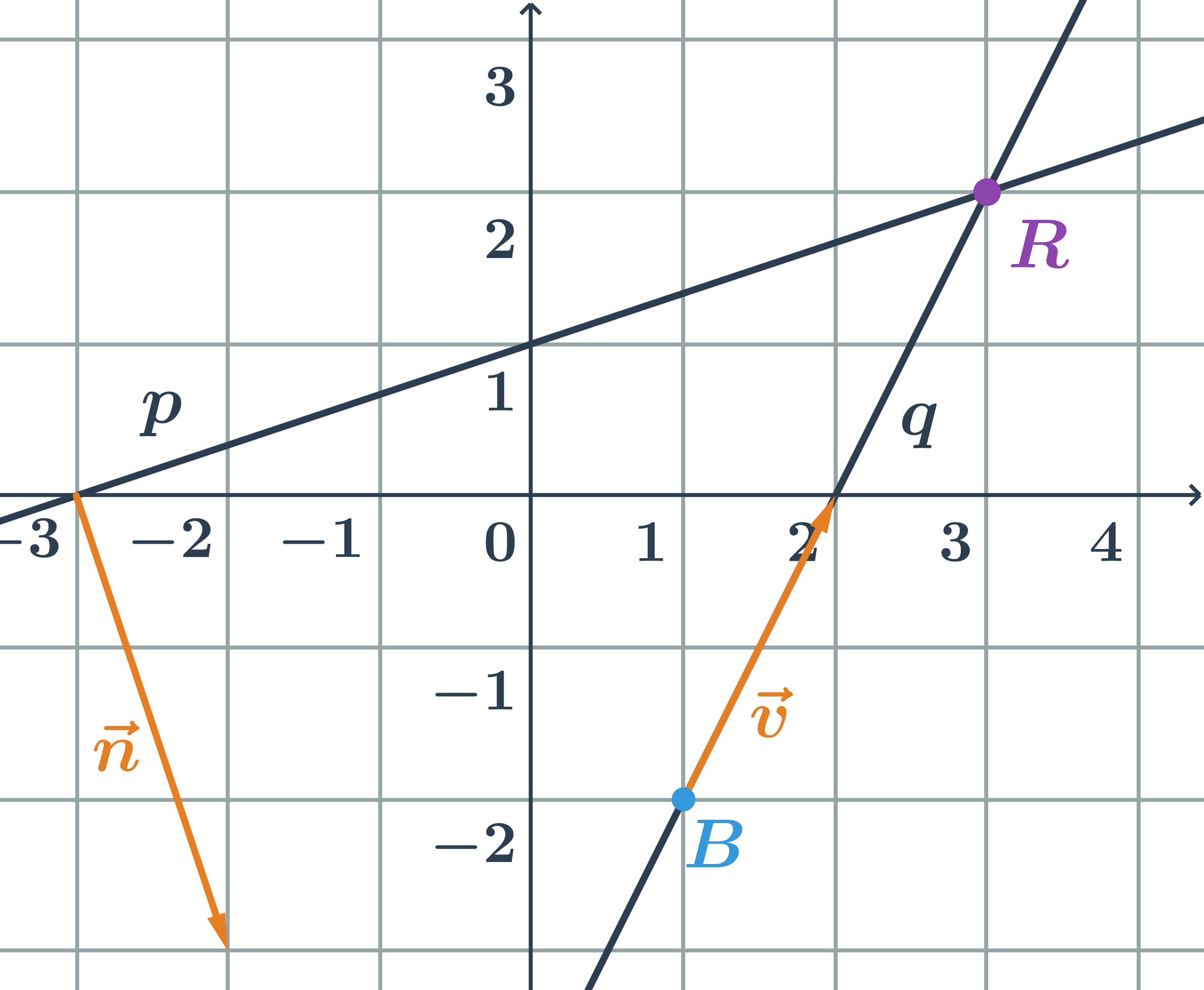
Souvislost počtu společných bodů přímek s počtem řešení soustavy rovnic
Pro určení společného bodu (bodů) dvou přímek, vždy řešíme soustavu rovnic. Tato soustava může mít:
- jedno řešení – přímky jsou různoběžné
- žádné řešení – přímky jsou rovnoběžné
- nekonečně mnoho řešení – přímky jsou totožné
Počet společných bodů – první příklad
Hledáme průsečík(y) přímek p,q zadaných jako: \hspace{0.25cm}p: x-3y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&\hspace{0.28cm}1+t\\y&=&-2+2t\end{array}
- Dosadíme parametrické vyjádření do obecné rovnice a řešíme soustavu rovnic:
\begin{array}{rrl}(1+t)-3(-2+2t)+3&=&0\\1+t+6-6t+3&=&0\\10-5t&=&0\\t&=&2\end{array}
- Jedno řešení \Rightarrow různoběžné přímky
Počet společných bodů – druhý příklad
Hledáme průsečík(y) přímek p,q zadaných jako: \hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&3-2t\\y&=&2-4t\end{array}
- Dosadíme parametrické vyjádření do obecné rovnice a řešíme soustavu rovnic:
\begin{array}{rrl}2(3-2t)-(2-4t)+3&=&0\\6-4t-2+4t+3&=&0\\7&=&0\end{array}
- Žádné řešení \Rightarrow různé rovnoběžné přímky
Počet společných bodů – třetí příklad
Hledáme průsečík(y) přímek p,q zadaných jako: \hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&3+t\\y&=&9+2t\end{array}
- Dosadíme parametrické vyjádření do obecné rovnice a řešíme soustavu rovnic:
\begin{array}{rrl}2(3+t)-(9+2t)+3&=&0\\6+2t-9-2t+3&=&0\\0&=&0\end{array}
- Nekonečně mnoho řešení \Rightarrow totožné přímky
Vzájemná poloha přímky a bodu v rovině
Bod leží na přímce, jestliže jeho souřadnice vyhovují rovnici přímky.
- Pokud je přímka daná obecnou rovnicí, po dosazení souřadnic bodu, který na přímce leží, do rovnice přímky nastane rovnost.
- Pokud je přímka daná parametricky, po dosazení souřadnic bodu vychází z obou rovnic stejná hodnota parametru t.
Bod a přímka daná obecnou rovnicí
Určete, zda body A=[2;3] a B=[-1;2] leží na přímce p:2x-3y+5=0.
- Do rovnice přímky dosadíme souřadnice bodu A=[2;3]:
- 2\cdot 2-3\cdot3+5=0 \Rightarrow bod A leží na přímce p
- Do rovnice přímky dosadíme souřadnice bodu B=[-1;2]:
- 2\cdot (-1)-3\cdot2+5=-3 \Rightarrow bod B neleží na přímce p
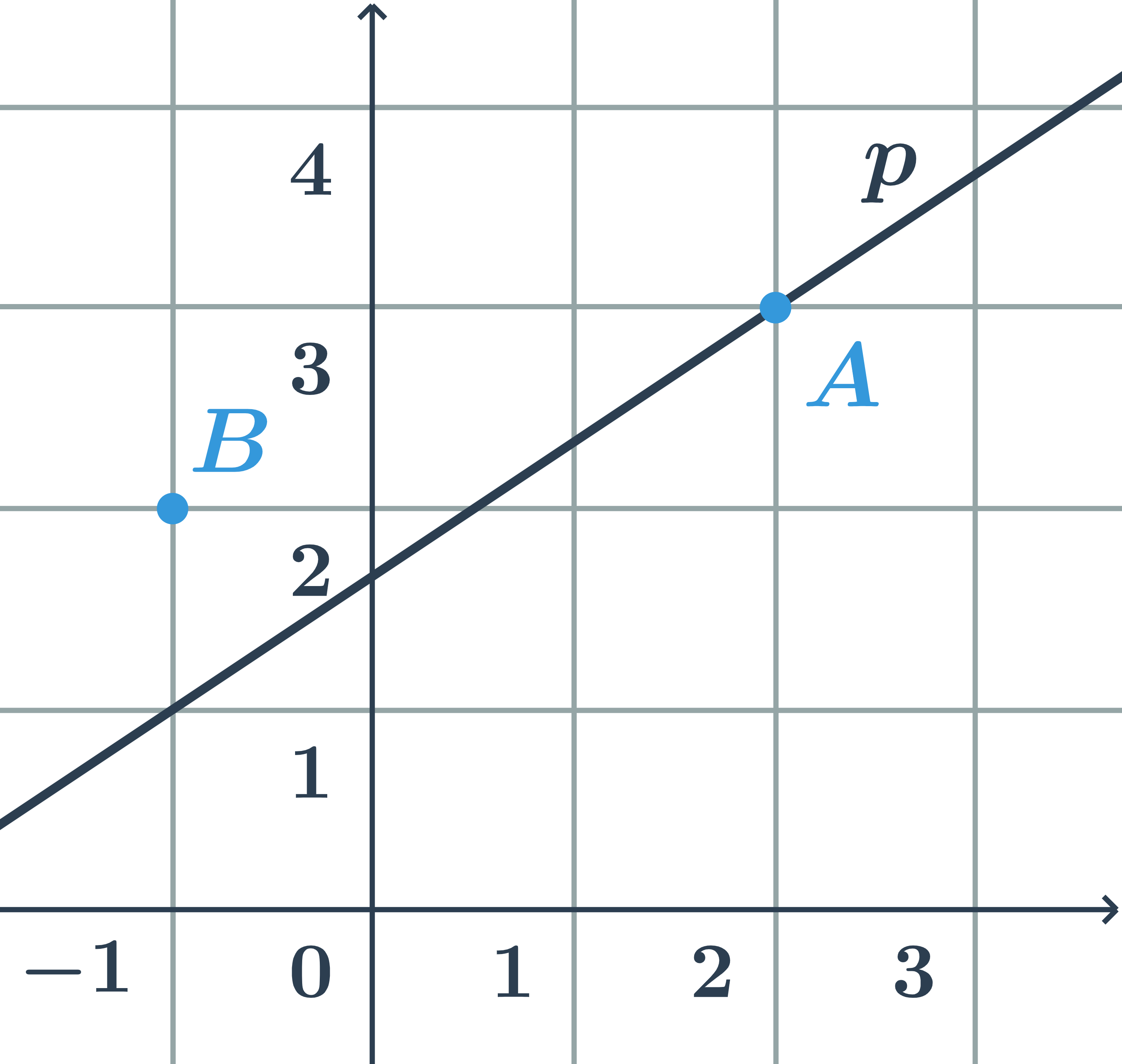
Bod a přímka daná parametricky
Určete, zda body A=[3;1] a B=[4;4] leží na přímce p dané parametricky: \begin{array}{rrl}x&=&2-t\\y&=&3+2t\\&&t\in\mathbb{R}\end{array}
- Do rovnic přímky dosadíme souřadnice bodu A=[3;1]:
\begin{array}{rrrr}3&=&2-t&\Rightarrow t=-1\\1&=&3+2t&\Rightarrow t=-1\end{array} \Rightarrow bod A leží na přímce p
- Do rovnice přímky dosadíme souřadnice bodu B=[4;5]:
\begin{array}{rrrl}4&=&2-t&\Rightarrow t=-2\\5&=&3+2t&\Rightarrow t=1\end{array}\Rightarrow bod B neleží na přímce p