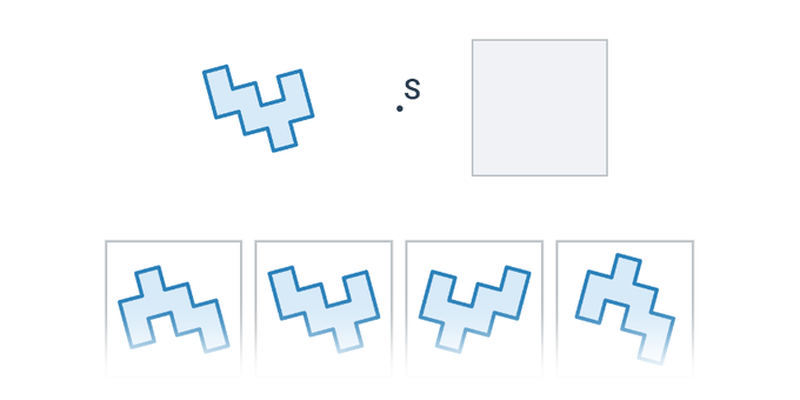
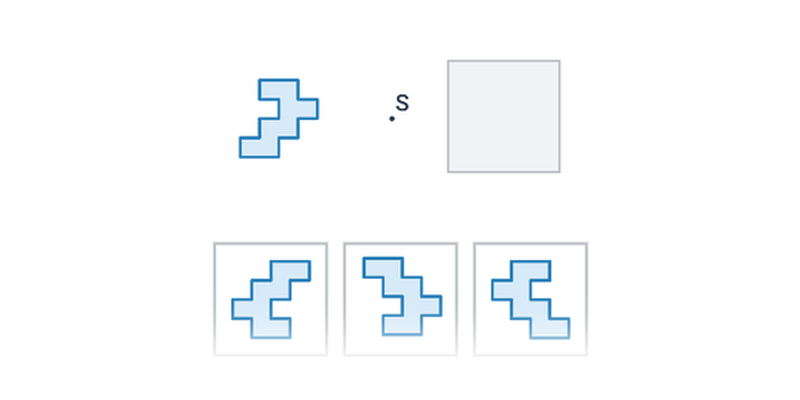
Středová souměrnost je dána bodem S a přiřazuje každému bodu X takový bod X', že bod S je středem úsečky XX'. Jinými slovy: obraz má od středu stejnou vzdálenost jako původní bod a leží na polopřímce opačné k SX.
Středová souměrnost zachovává vzdálenosti i úhly, jde tedy o druh shodnosti. Středová souměrnost se středem v bodě S je shodná s otočením o 180 stupňů podle středu S.
Příklady
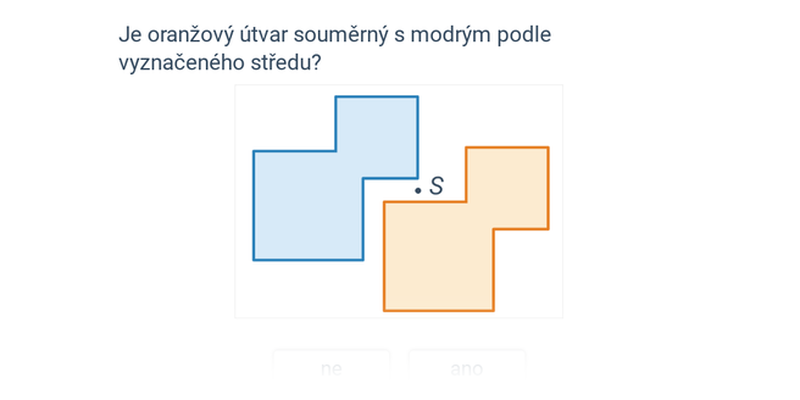
Modré a oranžové útvary jsou vzájemně středově souměrné podle středu S:
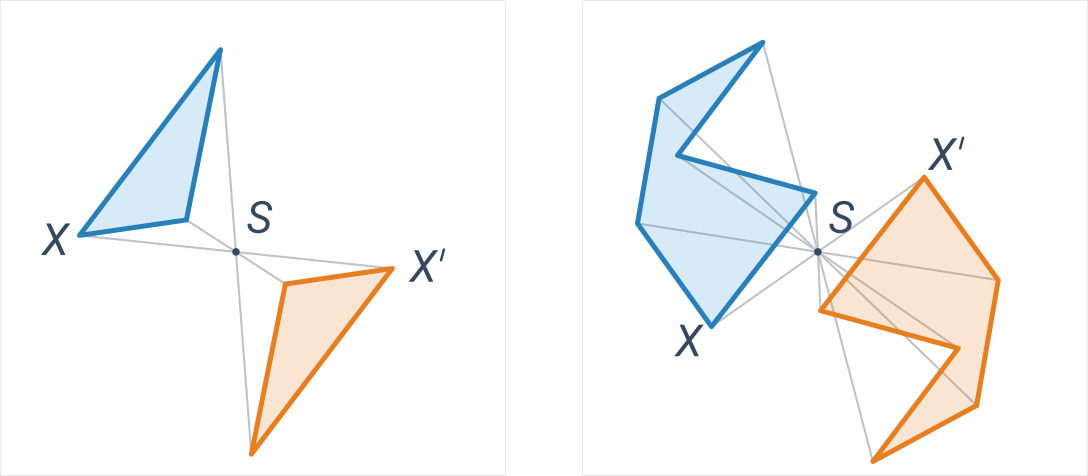
Pro lepší pochopení může být užitečné porovnat středovou a osovou souměrnost.
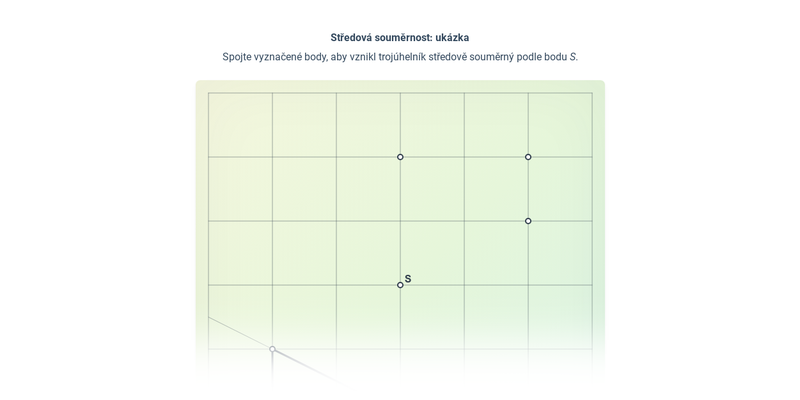
Středově souměrný útvar
Útvar označujeme za středově souměrný, pokud je v nějaké středové souměrnosti obrazem sebe sama. Střed této středové souměrnosti pak nazýváme středem souměrnosti objektu. Obrázek uvádí příklady útvarů středově souměrných (zelené, s vyznačeným středem souměrnosti) i těch nesouměrných (červené):
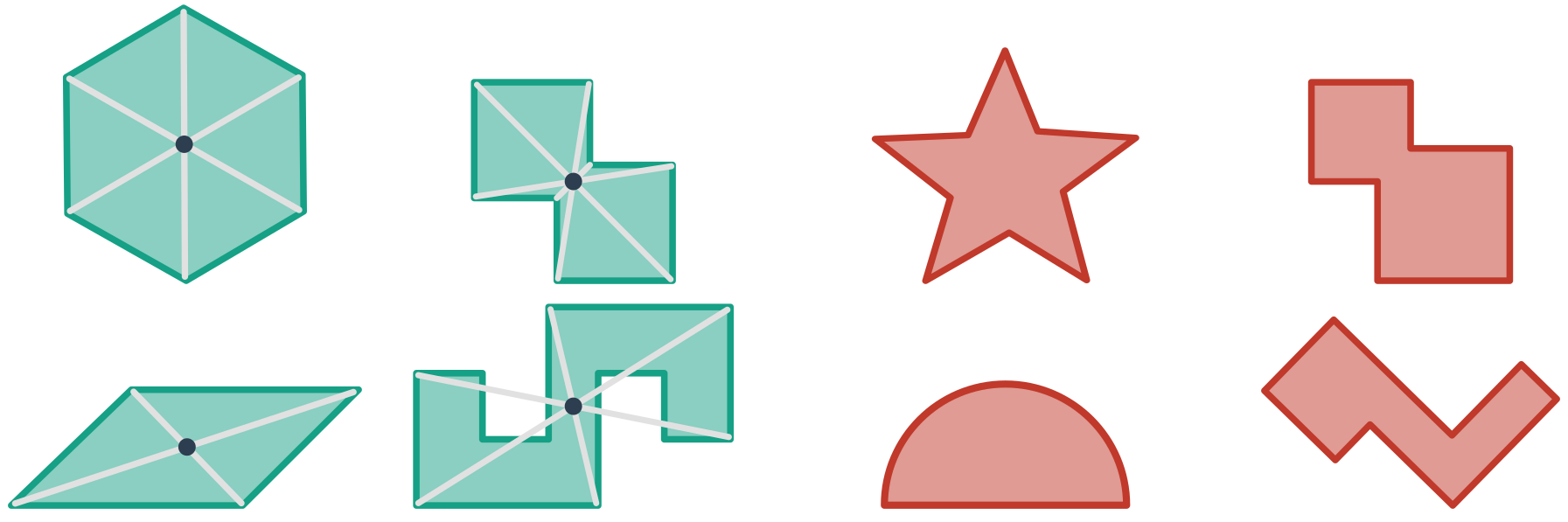
Další příklady:
Úsečka, obdélník, čtverec, kosočtverec, pravidelný šestiúhelník a kruh jsou středově souměrné.
Žádný trojúhelník není středově souměrný.
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Mřížkovaná
Úloha na procvičení geometrie s jednoduchým ovládáním a zajímavými úlohami.