Čeština
Angličtina
Informatika
Biologie
Němčina
Umíme to
Zeměpis
Chemie
Dějepis
Fyzika
ZSV
Aritmetika
Zlomky, procenta, desetinná čísla
Geometrie
Elementární algebra
Funkce
Jednotky, míry
Diskrétní matematika
Finanční gramotnost
Pexeso
Grafař
Porozumění
Označování
Mřížkovaná
Rozdělovačka
Rozbitá kalkulačka
Roboti
Střílečka
Příšerky
Závody
Územíčka
Tipovačka
Týmovka
Můj účet
Odhlásit se
- Kuželosečky
Všechny souhrny
Předcházející
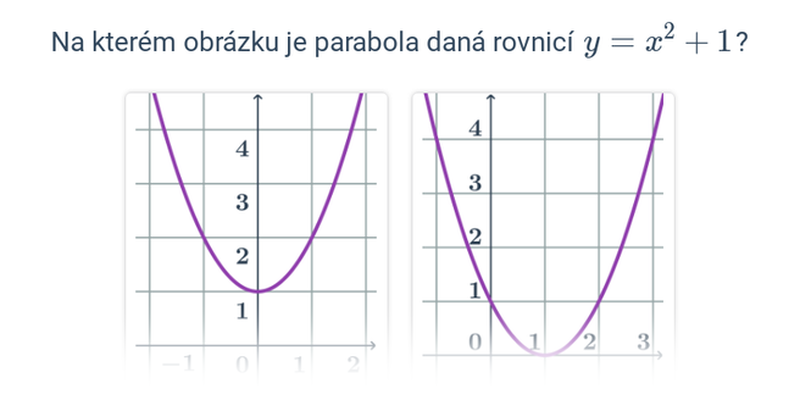
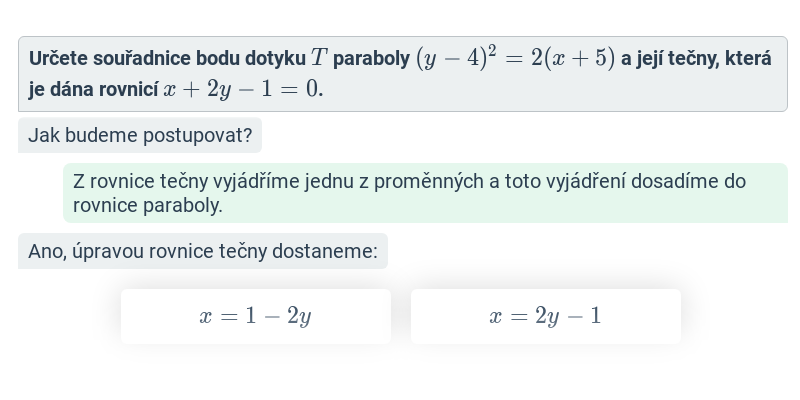
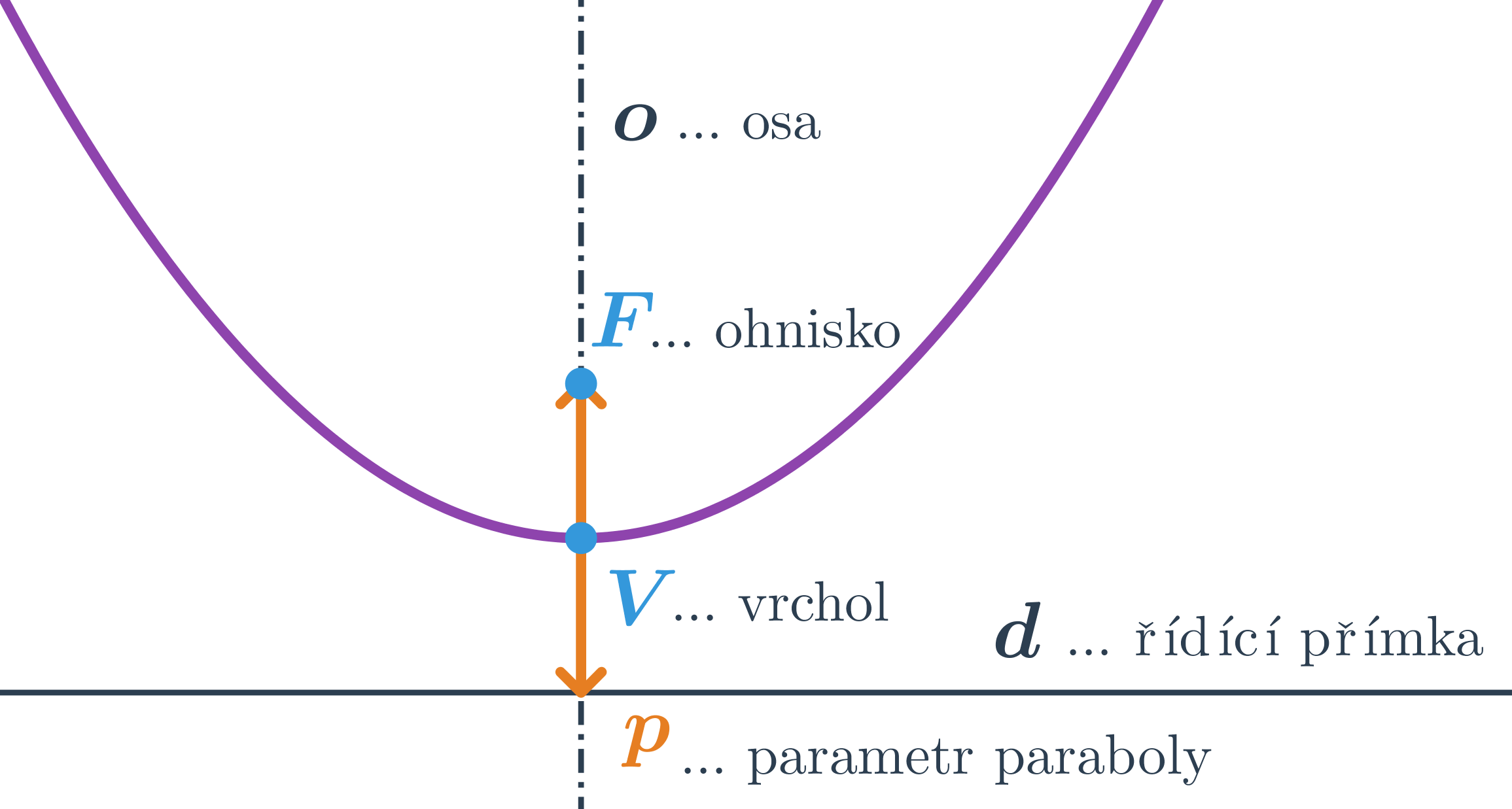
Parabola je množina všech bodů roviny, které mají stejnou vzdálenost od daného bodu (ohnisko) a dané přímky (řídící přímka)
Vrcholová rovnice paraboly
Tvar rovnice závisí na umístění osy:
- osa paraboly rovnoběžná s osou y, vrcholová rovnice pak má tvar: (x-m)^2=\pm 2p(y-n)
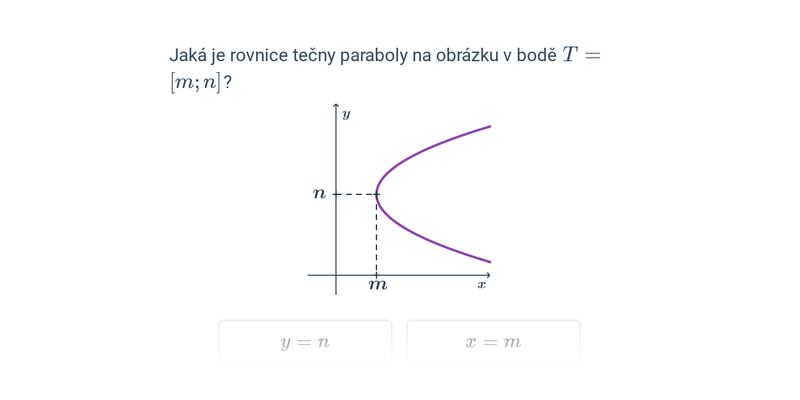
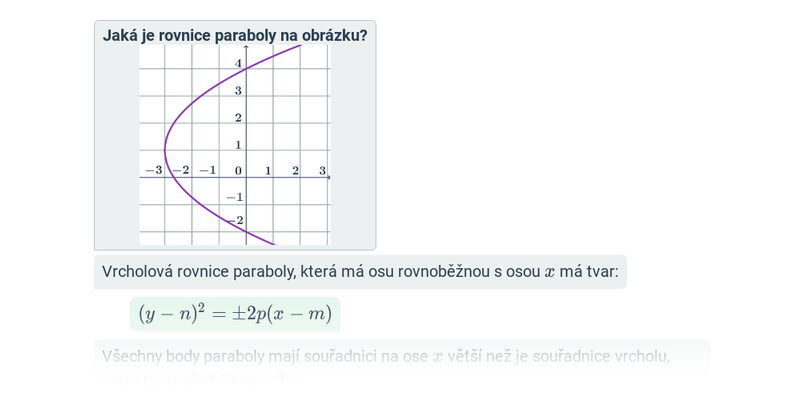
- osa paraboly rovnoběžná s osou x, vrcholová rovnice pak má tvar: (y-n)^2=\pm 2p(x-m)
V rovnici paraboly označují m, n souřadnice vrcholu paraboly, tedy vrchol je bod V=[m;n]. Dále p je parametr paraboly = vzdálenost ohniska od řídící přímky. Znaménko před parametrem závisí na poloze vrcholu vzhledem k bodům paraboly.
Příklad paraboly s osou rovnoběžnou s osou y
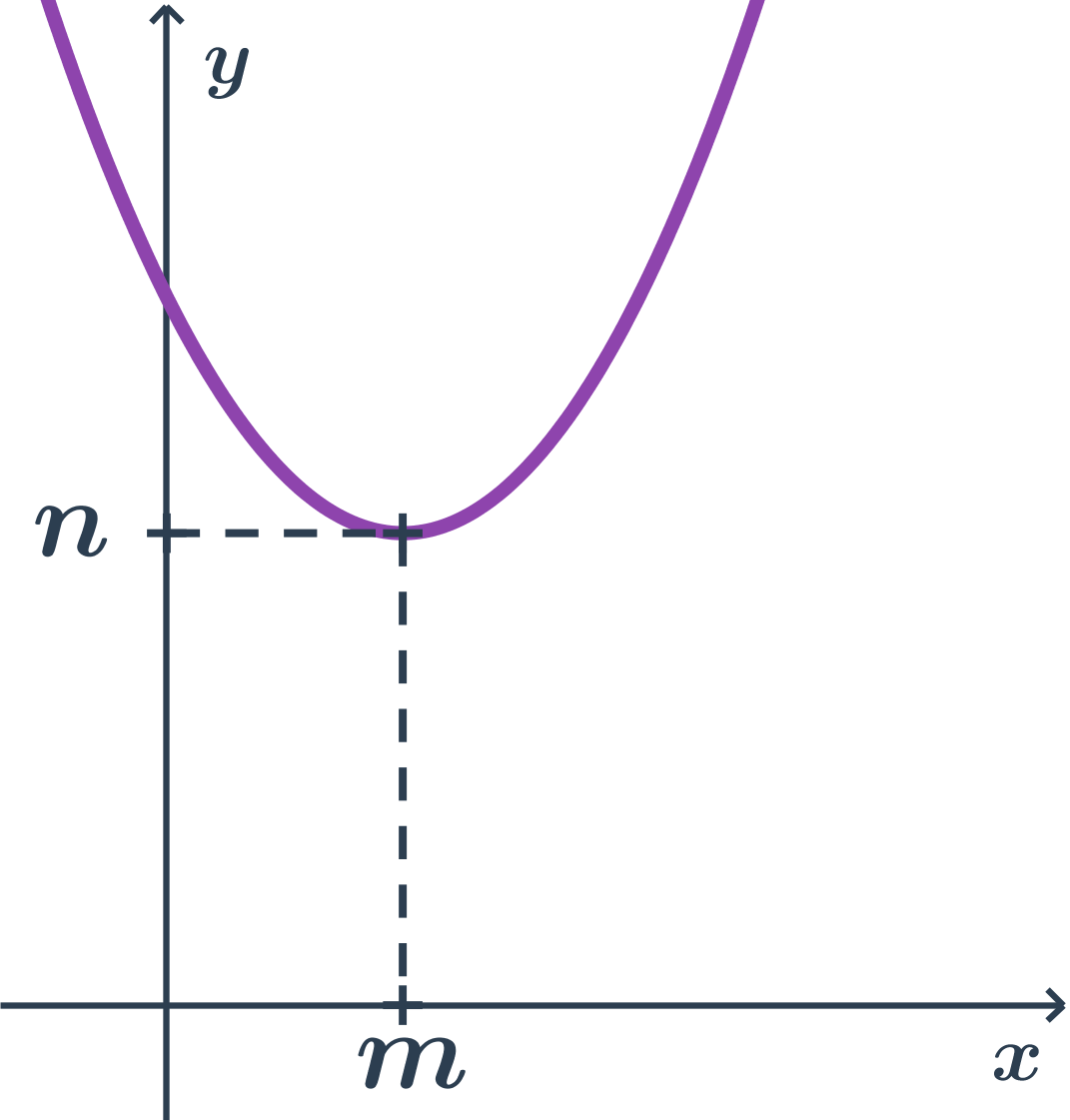
- body paraboly mají y souřadnici alespoň tak velkou jako vrchol (tj. n)
- vrcholová rovnice: (x-m)^2= + 2p(y-n)
Příklad paraboly s osou rovnoběžnou s osou y, druhá orientace
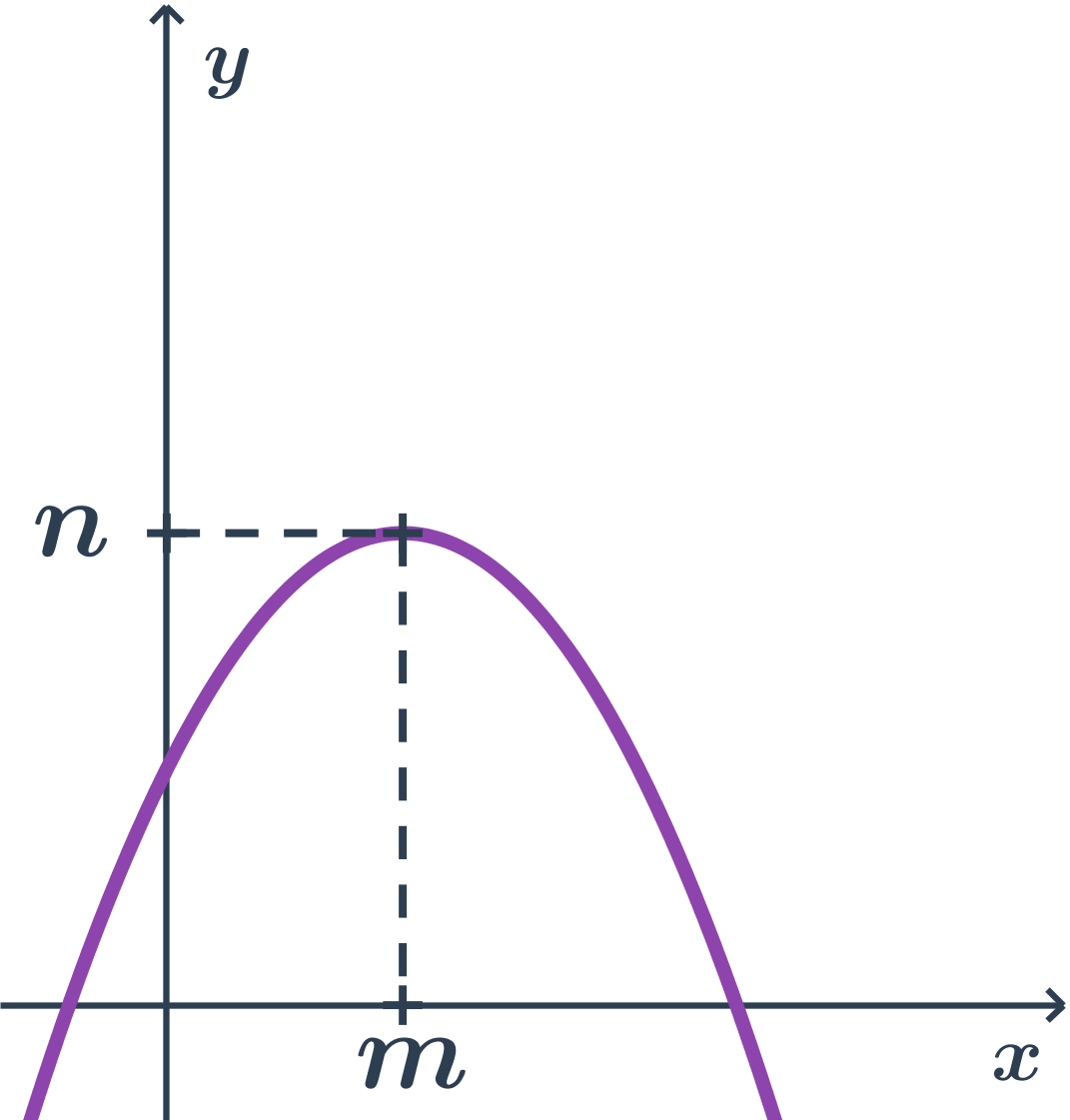
- body paraboly mají y souřadnici nejvýše tak velkou jako vrchol (tj. n)
- vrcholová rovnice: (x-m)^2= - 2p(y-n)
Příklad paraboly s osou rovnoběžnou s osou x
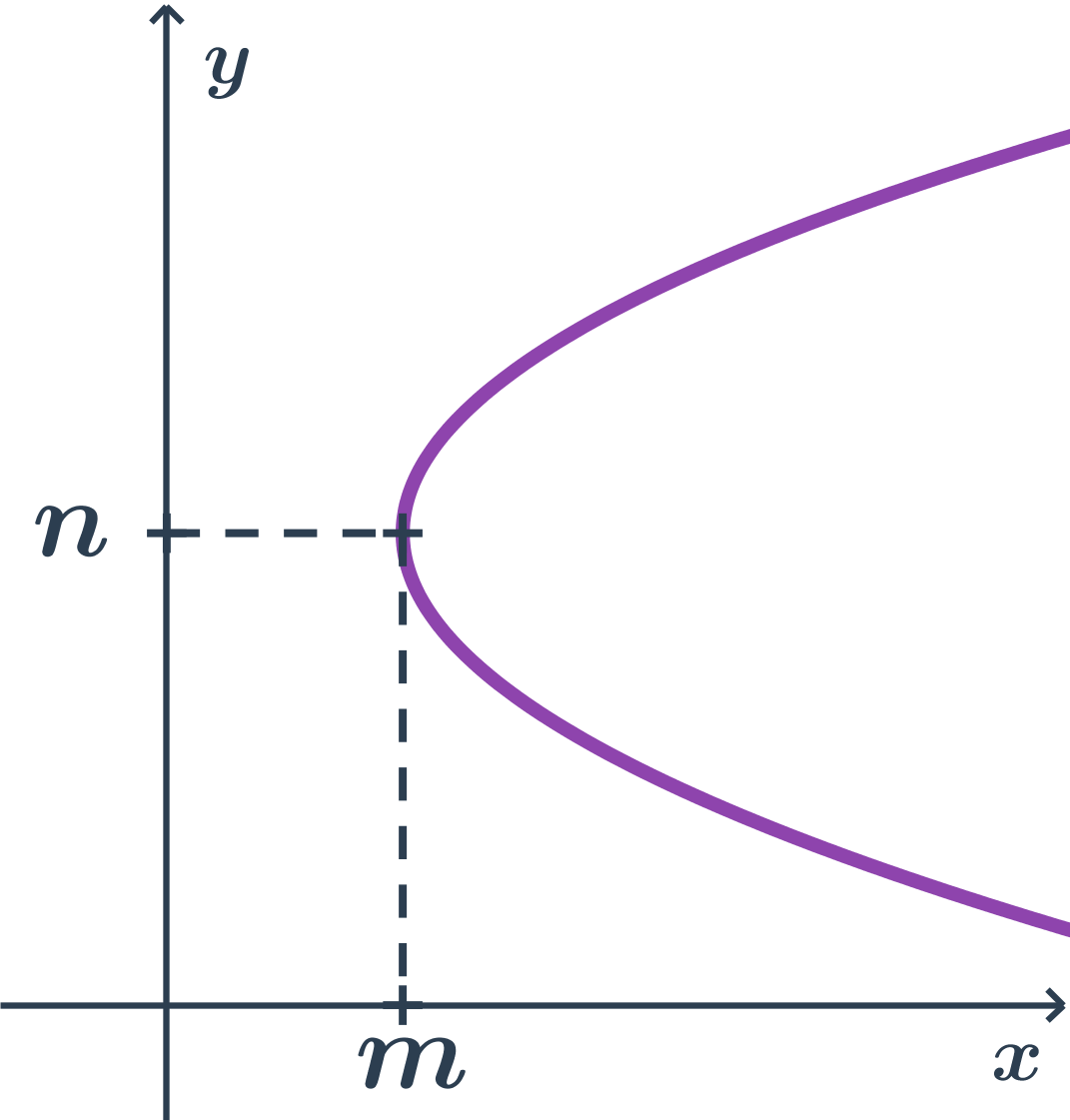
- body paraboly mají x souřadnici alespoň tak velkou jako vrchol (tj. m)
- vrcholová rovnice: (y-n)^2= + 2p(x-m)
Příklad paraboly s osou rovnoběžnou s osou x, druhá orientace
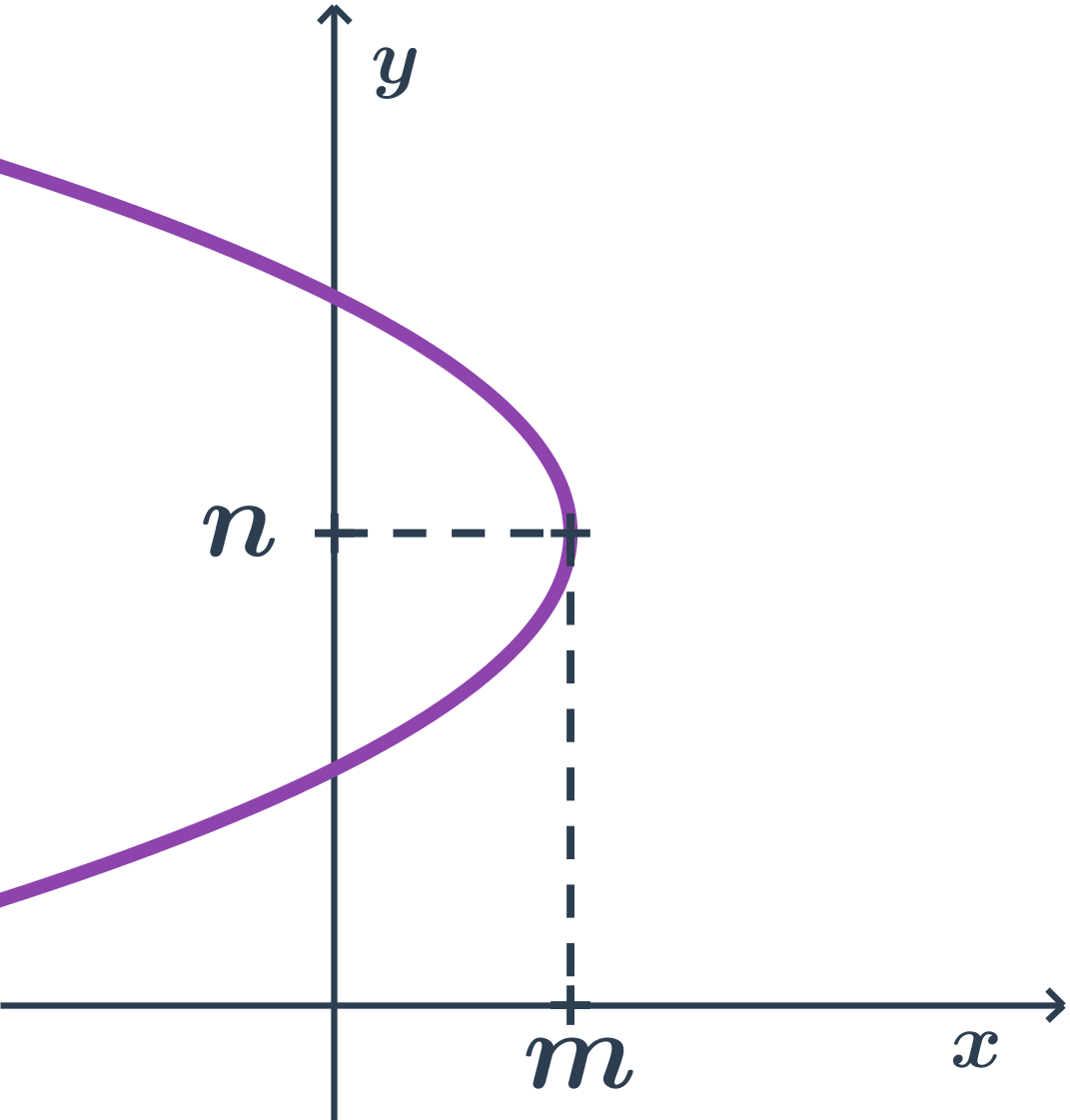
- body paraboly mají x souřadnici nejvýše tak velkou jako vrchol (tj. m)
- vrcholová rovnice: (y-n)^2= - 2p(x-m)
Obecná rovnice paraboly
Tvar rovnice závisí na umístění osy:
- osa paraboly je rovnoběžná s osou y: y=ax^2+bx+c
- osa paraboly je rovnoběžná s osou x: x=ay^2+by+c
Příklad paraboly s osou rovnoběžnou s osou y, obecná rovnice
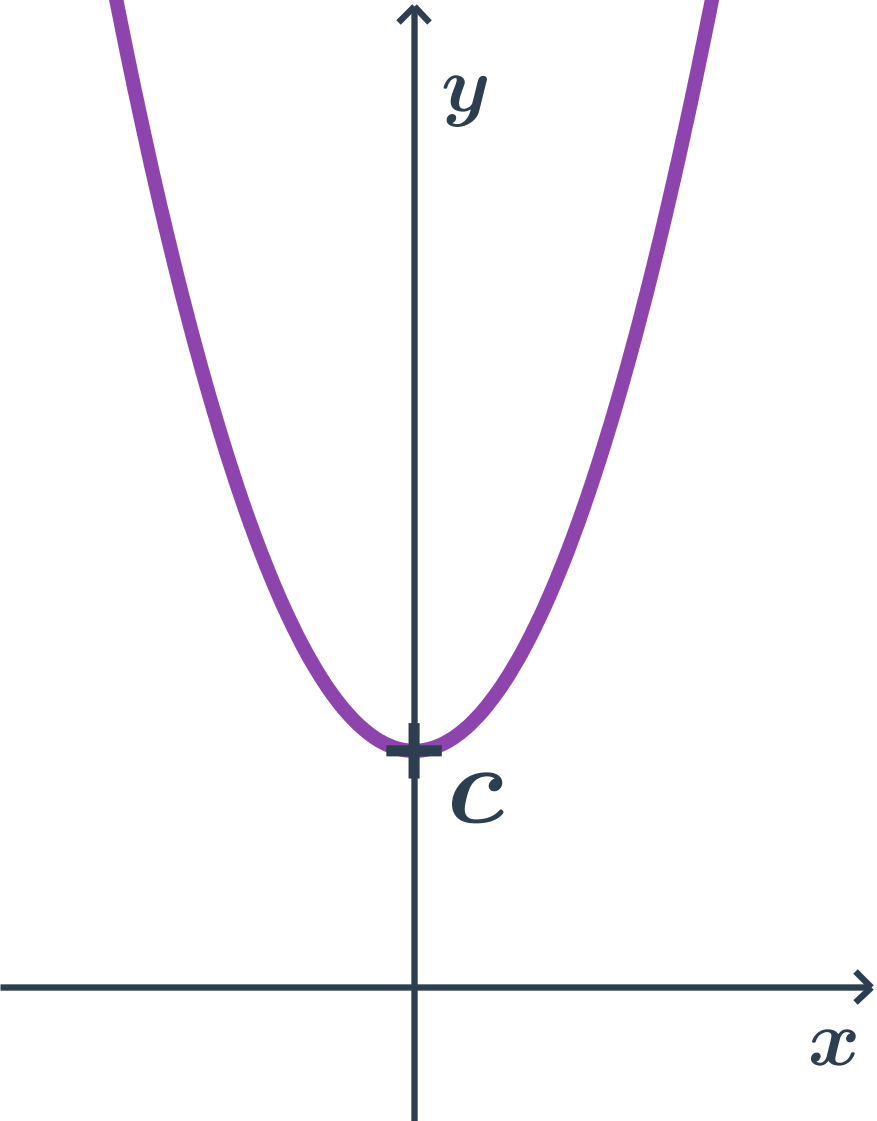
- obecná rovnice: y=ax^2+bx+c
- kde a \gt 0
Příklad paraboly s osou rovnoběžnou s osou y, druhá orientace, obecná rovnice
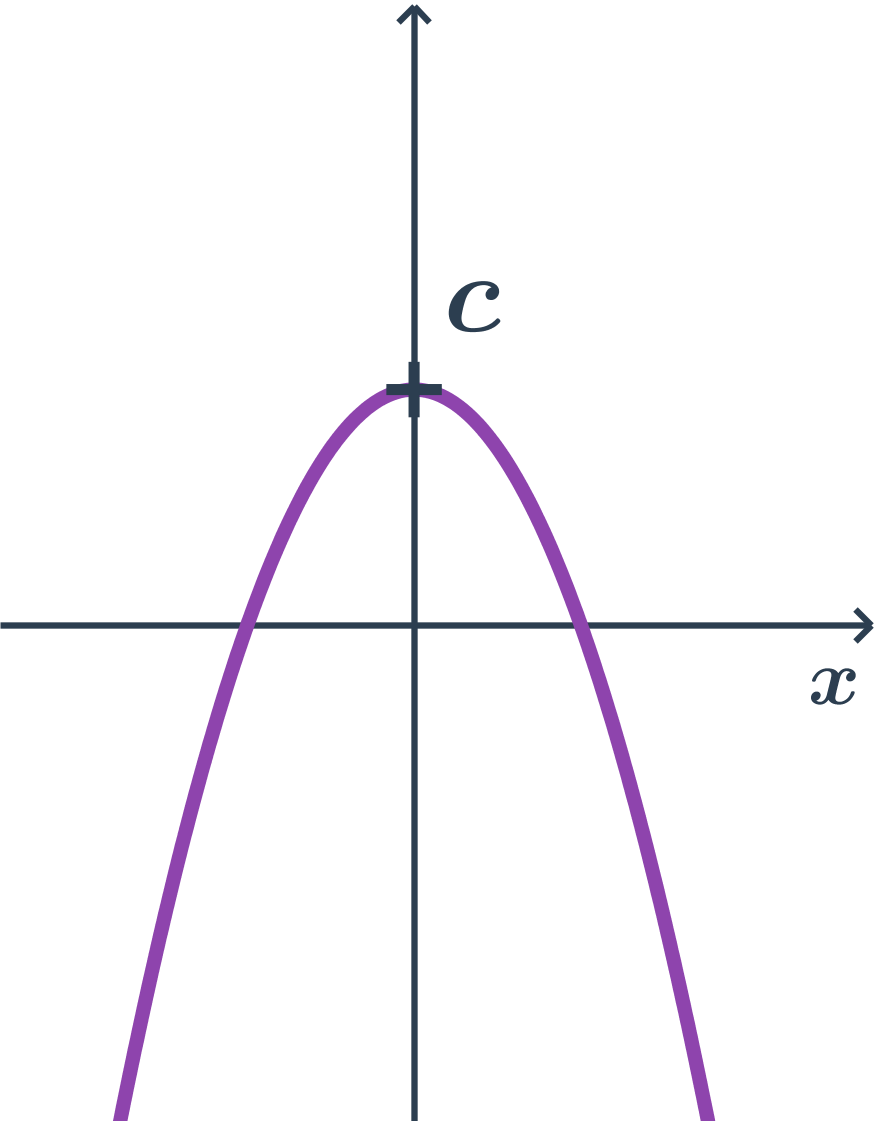
- obecná rovnice: y=ax^2+bx+c
- kde a \lt 0
Příklad paraboly s osou rovnoběžnou s osou x, obecná rovnice
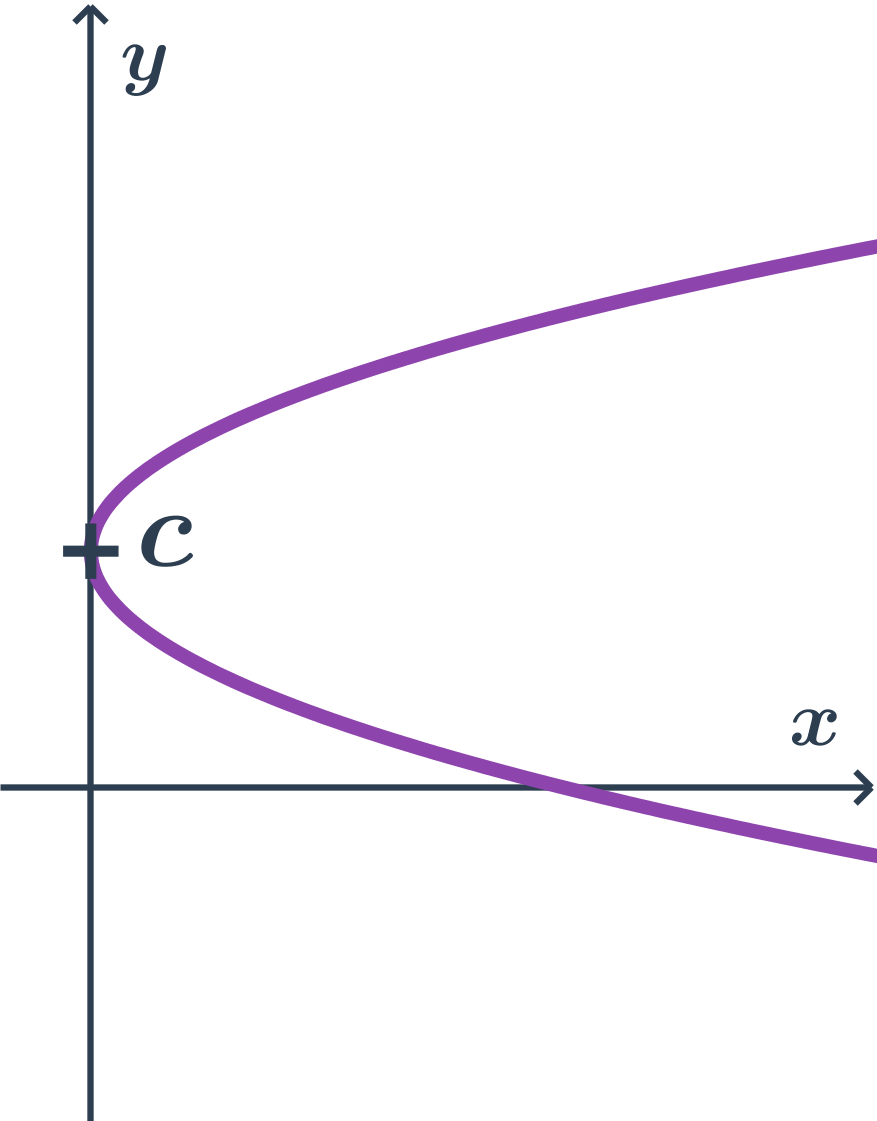
- obecná rovnice: x=ay^2+by+c
- kde a \gt 0
Příklad paraboly s osou rovnoběžnou s osou x, druhá orientace, obecná rovnice
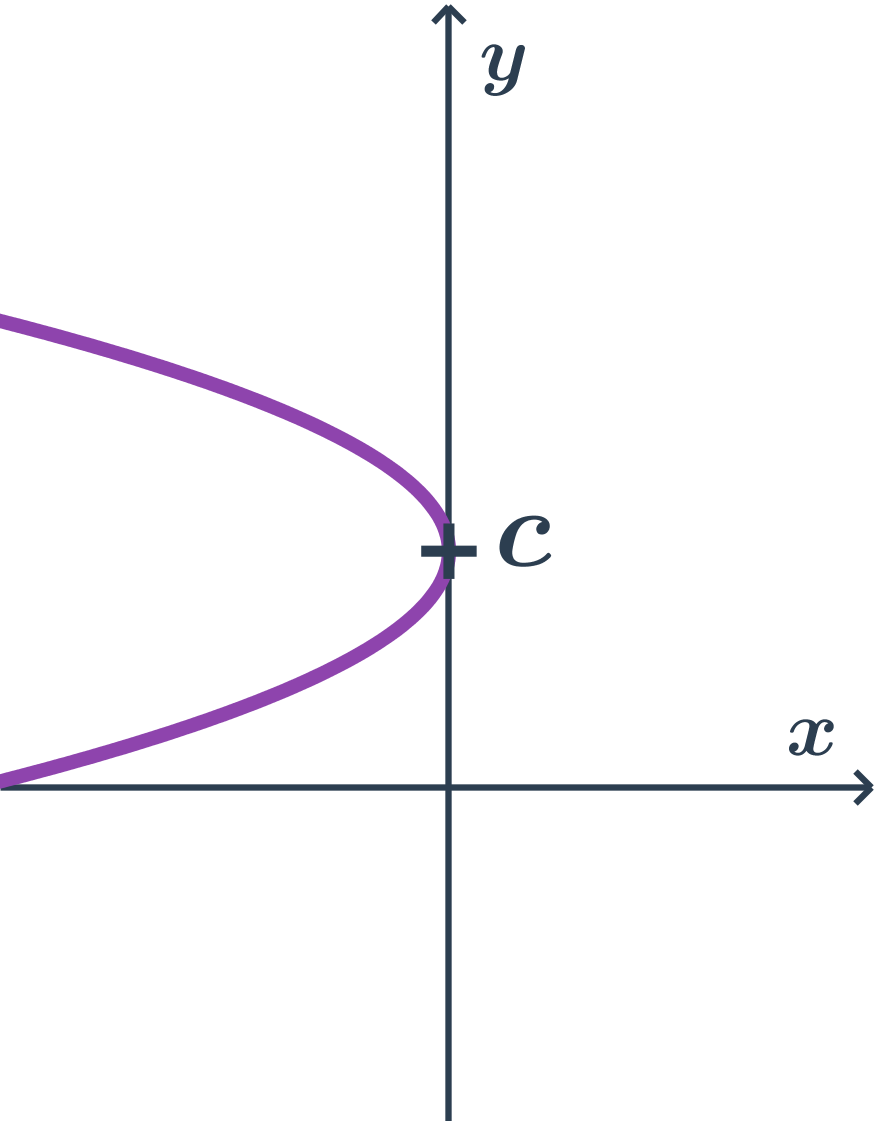
- obecná rovnice: x=ay^2+by+c
- kde a \lt 0
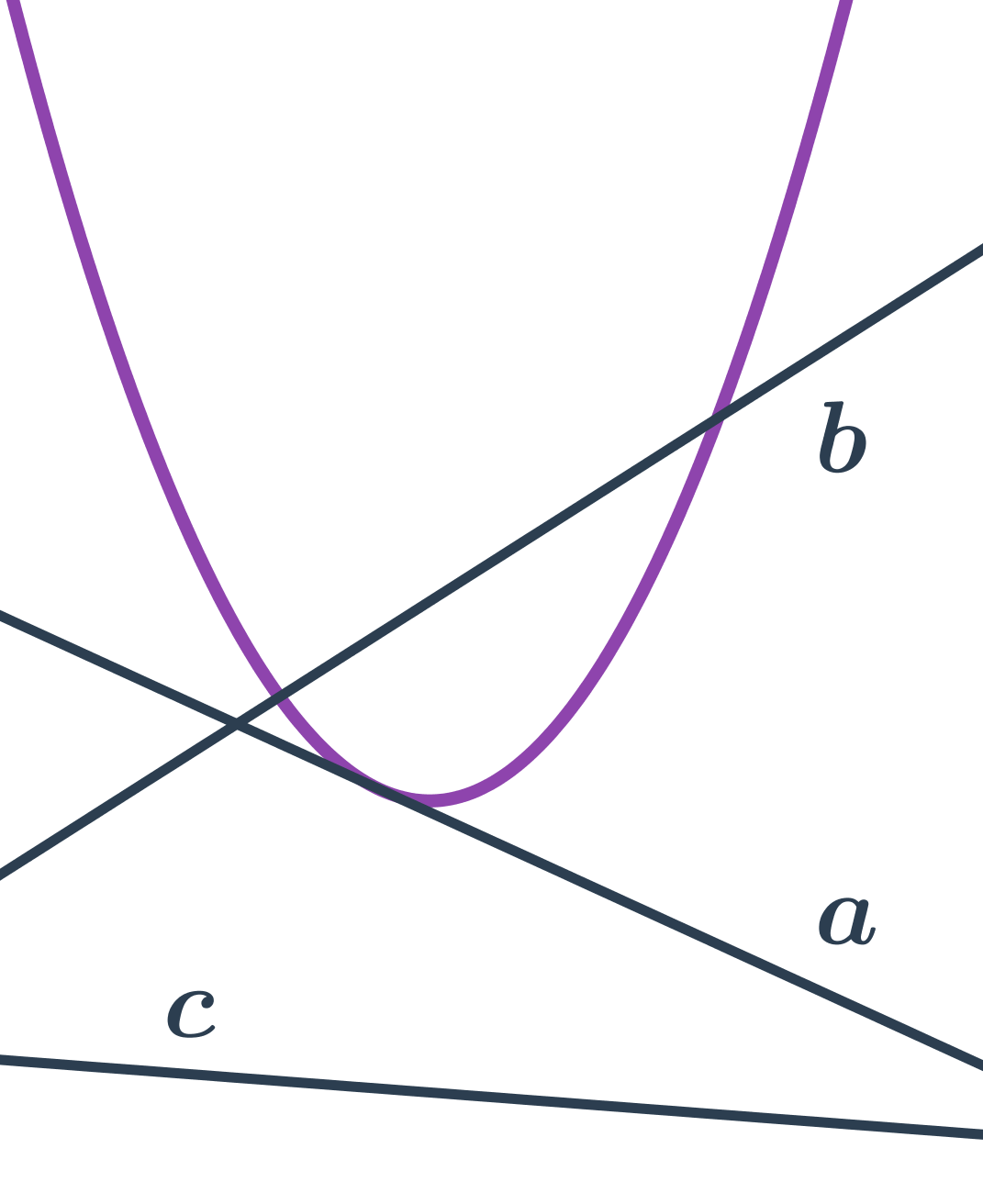
Přímka a parabola
- přímka b protíná parabolu ve dvou bodech – sečna paraboly
- přímka a se dotýká paraboly v jednom bodě – tečna paraboly
- přímka c neprotíná parabolu
Rovnice tečny paraboly v bodě, který leží na parabole
- parabola daná rovnicí (x-m)^2=\pm 2p(y-n) má v bodě T=[x_0;y_0] tečnu danou rovnicí: (x_0 - m)(x - m)=\pm p(y_0 - n) \pm p(y - n)
- parabola daná rovnicí (y-n)^2=\pm 2p(x-m) má v bodě T=[x_0;y_0] tečnu danou rovnicí: (y_0 - n)(y - n)=\pm p(x_0 - m)\pm p(x - m)
Příklad tečny paraboly v bodě
- mějme parabolu danou vrcholovou rovnicí: (x-2)^2=2(y-1)
- pro tuto parabolu je m=2, n=1, p=1
- na této parabole leží (souřadnice splňují rovnici) například bod T=[4;3]
- tečna dané paraboly v bodě T=[4;3] má rovnici: (4 - 2)(x - 2)= (3 - 1) + (y - 1)
- rovnici tečny můžeme zjednodušit na 2x-4 = y+1, tedy y = 2x-5
Druhý příklad tečny paraboly v bodě
- mějme parabolu danou vrcholovou rovnicí: (x-2)^2= - 4(y-1)
- pro tuto parabolu je m=2, n=1, p=2, pravá strana je ve formě -2p(y-n)
- na této parabole leží (souřadnice splňují rovnici) například bod T=[6;-3]
- tečna dané paraboly v bodě T=[6;-3] má rovnici: (6-2)(x-2)= -2(-3-1)-2(y-1)
- rovnici tečny můžeme zjednodušit na 4x-8 = 8 -2y+2, tedy y = -2x+9
Speciální poloha přímky a paraboly
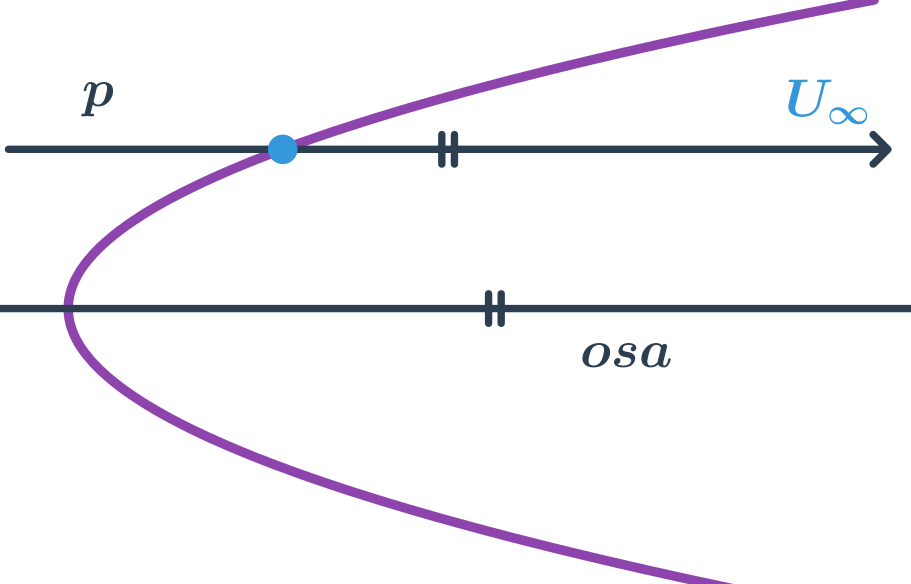
Přímka rovnoběžná s osou paraboly je sečna paraboly, přestože se zdá, že má s parabolou jeden společný bod. Druhý společný bod má tato přímka a parabola v nekonečnu.
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
Parabola: rovnice (střední)
zadání: 12
Typicky zabere: 10 min
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Parabola: rovnice (střední)
zadání: 30
Typicky zabere: 8 min
Parabola: tečna (střední)
zadání: 30
Typicky zabere: 6 min
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
Parabola: rovnice (střední)
zadání: 15
Typicky zabere: 11 min
Parabola: tečna (střední)
zadání: 15
Typicky zabere: 5 min
Parabola: vzájemná poloha přímky a paraboly (střední)
zadání: 15
Typicky zabere: 7 min
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.
Parabola (střední)
zadání: 30
Typicky zabere: 8 min
