Kužel
GDXKužel je prostorový geometrický útvar s kruhovou podstavou. Zužuje se směrem k jednomu bodu zvanému vrchol. Jde o útvar, který vznikne, když se kolem své osy otáčí rovnoramenný trojúhelník. Příkladem kuželu v běžném životě je kornout zmrzliny nebo dopravní kužel.
Vzorce pro objem a povrch
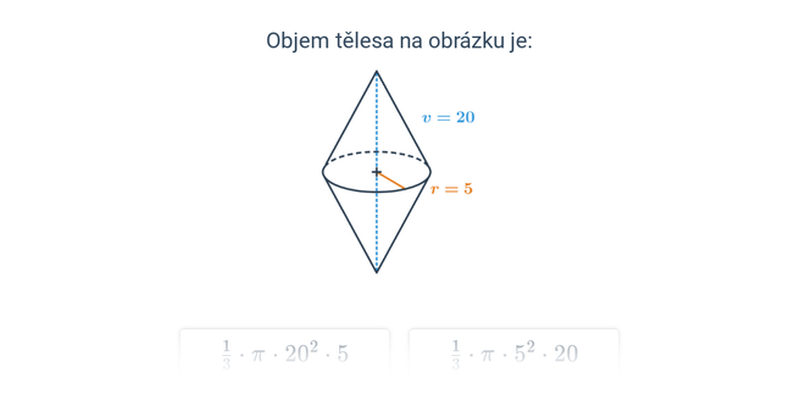
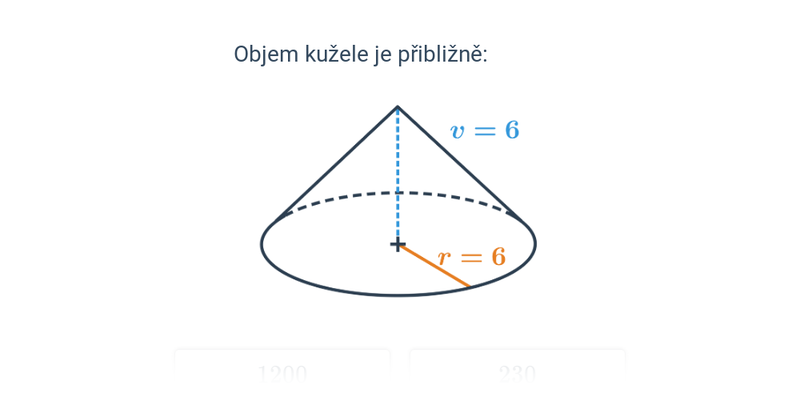
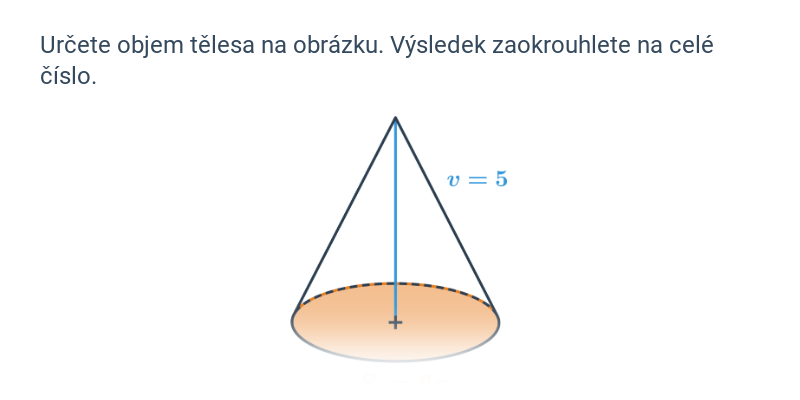
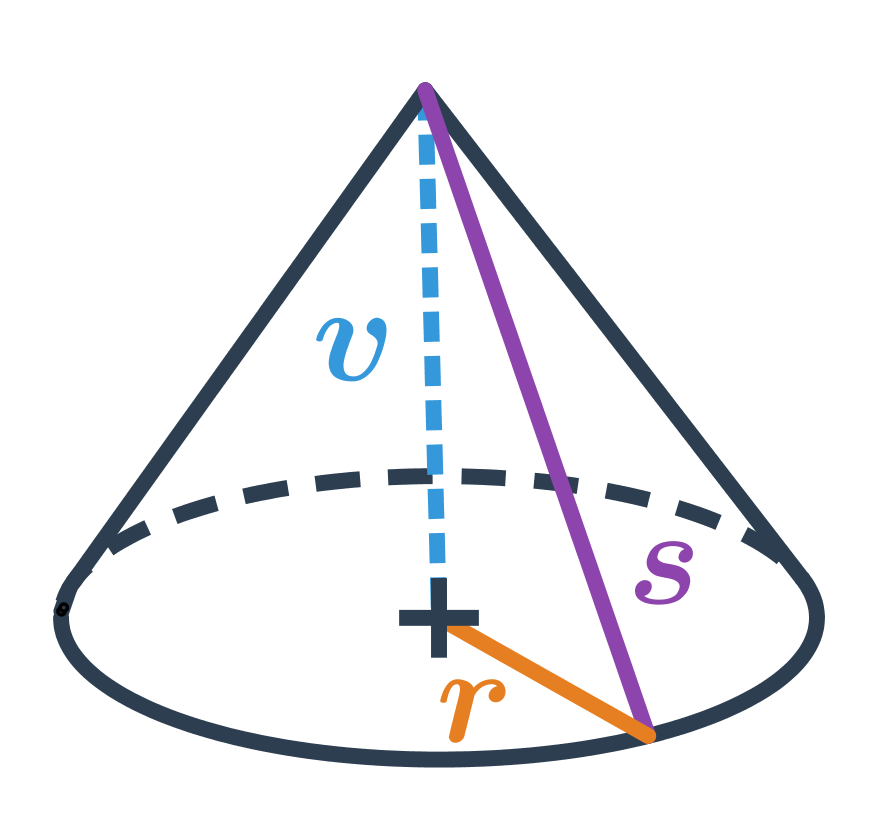
Objem kuželu lze vypočítat pomocí vzorce: V = \frac{1}{3} \pi \cdot r^2 \cdot v, kde r je poloměr podstavy a v je výška kuželu, což je vzdálenost vrcholu od roviny, ve které leží podstava kuželu.
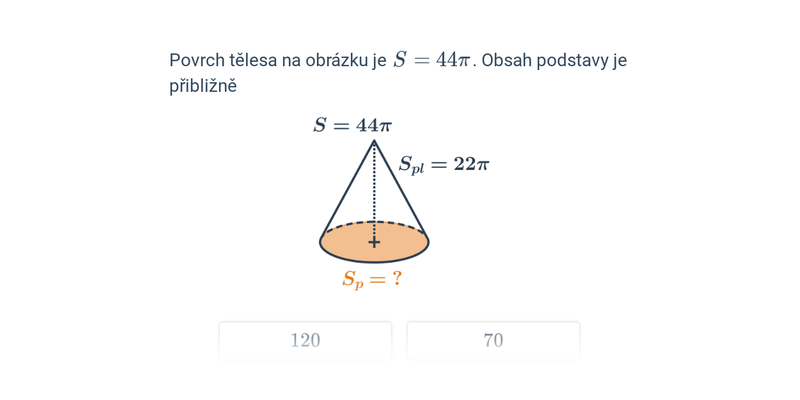
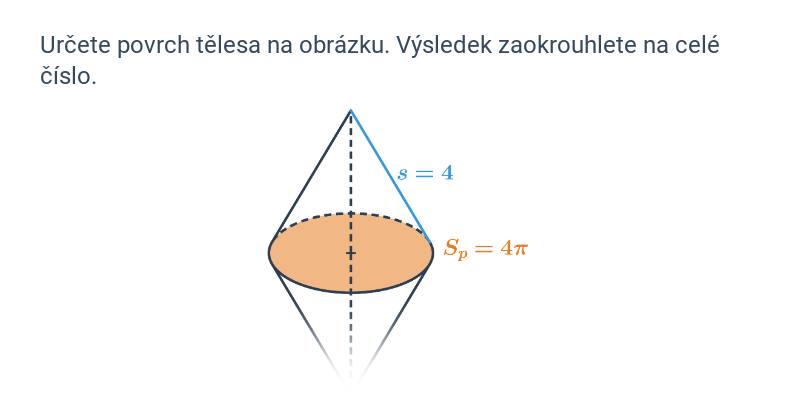
Povrch kuželu získáme sečtením obsahu základny a obsahu pláště S = \pi \cdot r^2 + \pi \cdot r s, kde s je tzv. strana kuželu, což je délka úsečky spojující vrchol kuželu s okrajem jeho základny.
Kuželosečky
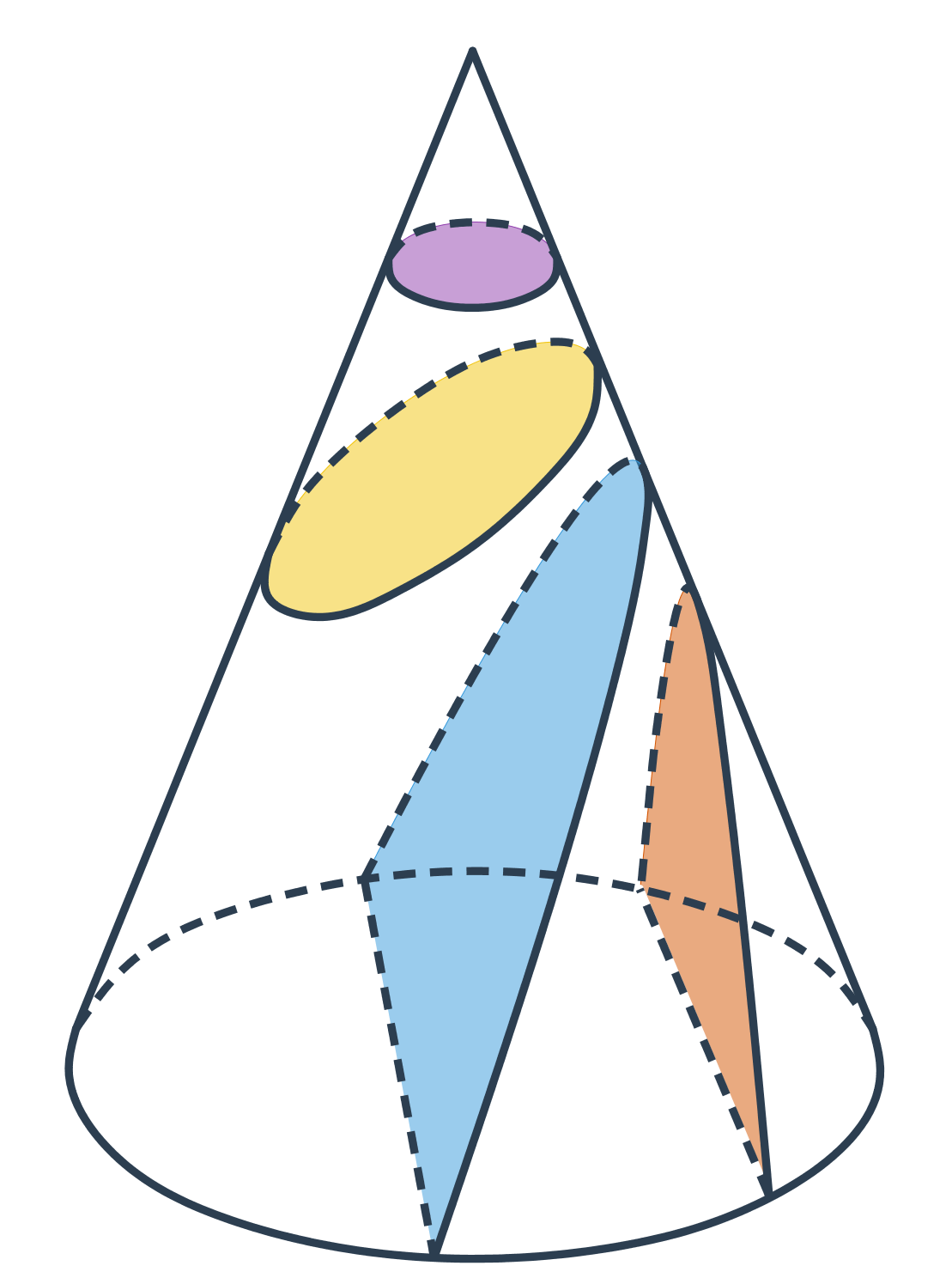
Křivky, které vznikají průnikem kuželového povrchu s rovinou se nazývají kuželosečky. Patří mezi ně například kružnice, elipsa, parabola a hyperbola.
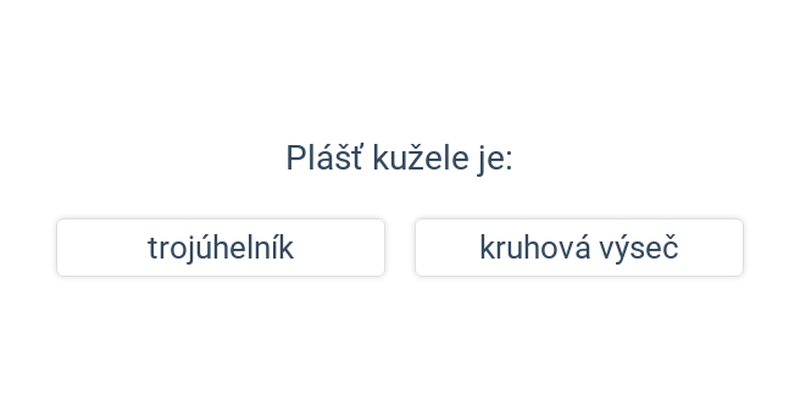
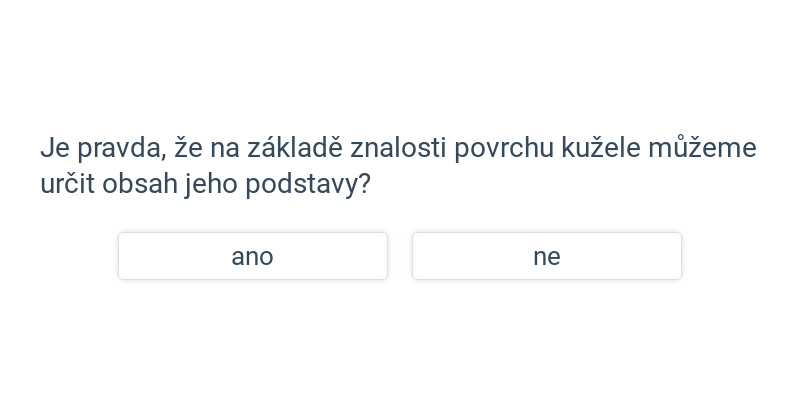
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.