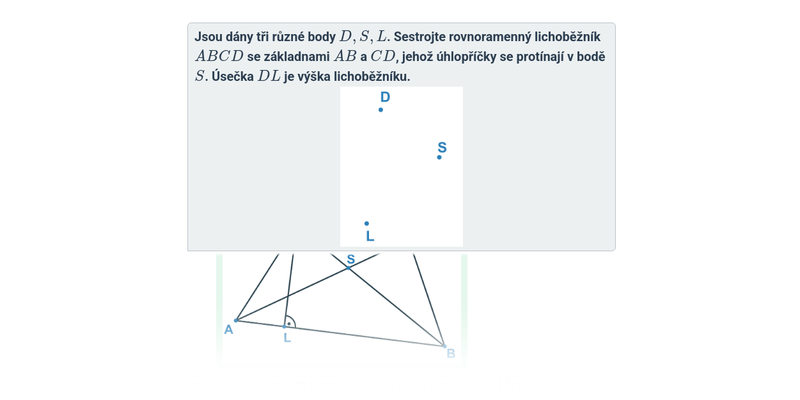
Konstrukce lichoběžníků
Lichoběžník je čtyřúhelník, který má dvě rovnoběžné strany – ty se nazývají základny a dvě různoběžné strany – ramena. Vzdálenost základen se nazývá výška. Při konstrukcích budeme využívat následující vlastnosti:
- Základny jsou rovnoběžné.
- Úsečka spojující středy ramen se nazývá střední příčka a je rovnoběžná se základnami.
- Součet vnitřních úhlů u každého ramene je 180°.

Při konstrukci lichoběžníku potřebujeme znát čtyři údaje, ze kterých často dokážeme sestrojit trojúhelník určený podle vět s vrcholy ve třech vrcholech lichoběžníku. Zbývající vrchol lichoběžníku pak najdeme pomocí posledního údaje a rovnoběžnosti základen.
Příklad: konstrukce lichoběžníku, známé délky tří stran a úhlopříčky
Sestrojte lichoběžník ABCD, je-li dáno a=8 cm, b=6 cm, c=5 cm, |AC|=8 cm.
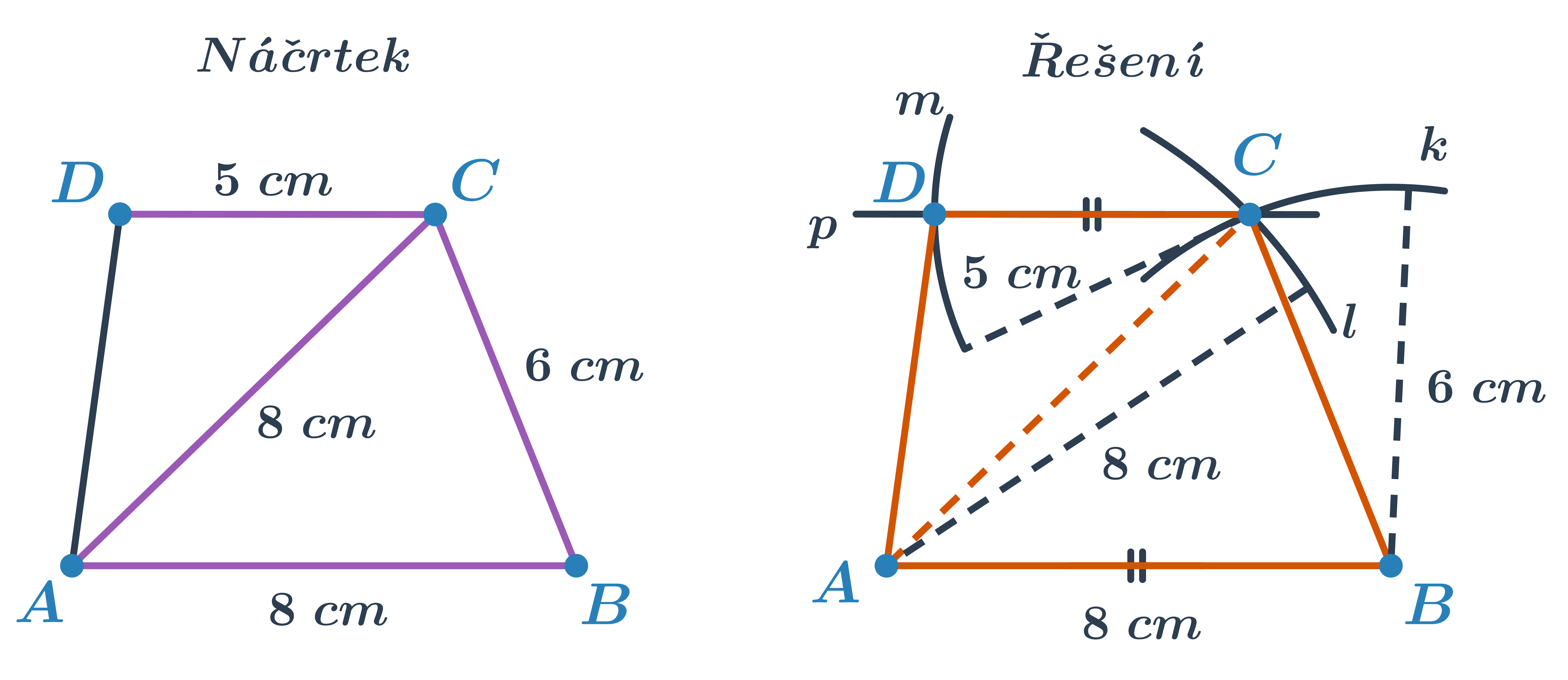
- Nejprve sestrojíme trojúhelník ABC určený podle věty sss.
- Základna CD je rovnoběžná se základnou AB. Bodem C tedy sestrojíme rovnoběžku p se stranou AB.
- Na tuto rovnoběžku pak naneseme délku strany c – poslední známý údaj.
Konstrukce rovnoramenných lichoběžníků
V rovnoramenném lichoběžníku mají obě ramena stejnou délku. Odpovídající vnitřní úhly u těchto ramen jsou pak stejné (dva stejné úhly \alpha = \beta u jedné základny a dva stejné úhly \gamma=\delta=180^\circ - \alpha u druhé základny). Úhlopříčky rovnoramenného lichoběžníku jsou stejně dlouhé. Narozdíl od obecného lichoběžníku mu lze opsat kružnici. Střed této opsané kružnice ale neleží v průsečíku úhlopříček.
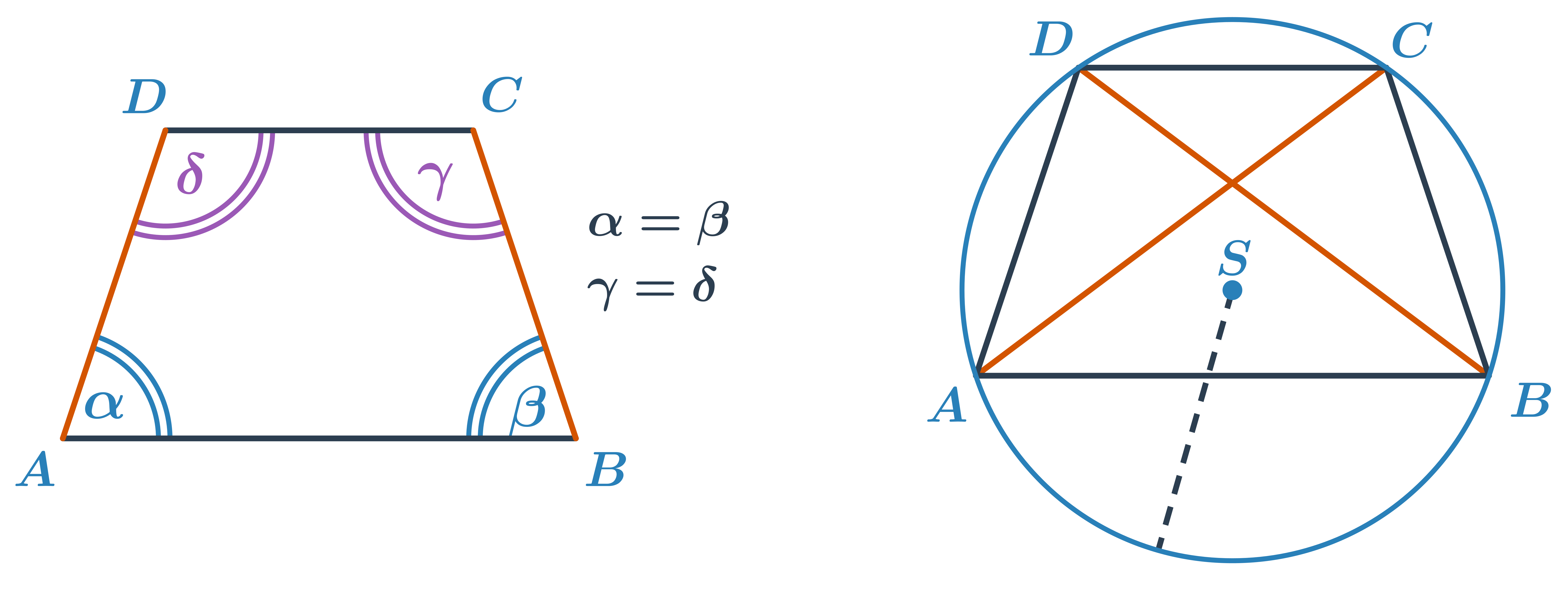
Kromě interaktivního procvičování níže je k dispozici ještě pracovní list k vytištění a rýsování na papíře:
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.