Výpis souhrnů
Konstrukční úlohy: čtyřúhelníky
Podtémata
Konstrukční úlohy: čtyřúhelníky
Téma je rozděleno podle typů konstruovaných čtyřúhelníků:
- Konstrukce čtverců a obdélníků – základní konstrukce čtyřúhelníků, které mají všechny vnitřní úhly pravé
- Konstrukce rovnoběžníků – konstrukce čtyřúhelníků se dvěma dvojicemi rovnoběžných protějších stran
- Konstrukce lichoběžníků – konstrukce čtyřúhelníků s jednou dvojicí rovnoběžných protějších stran
- Konstrukce obecných čtyřúhelníků – konstrukce čtyřúhelníků, o kterých víme jen to, co si přečteme v zadání příkladu, nemusí splňovat žádné další podmínky
Kromě interaktivních cvičení jsou u jednotlivých témat k dispozici také pracovní listy k vytištění a rýsování na papíře:
Všechny pracovní listy na konstrukce čtyřúhelníků
Konstrukce čtyřúhelníků: čtverce a obdélníky
Konstrukce obdélníků
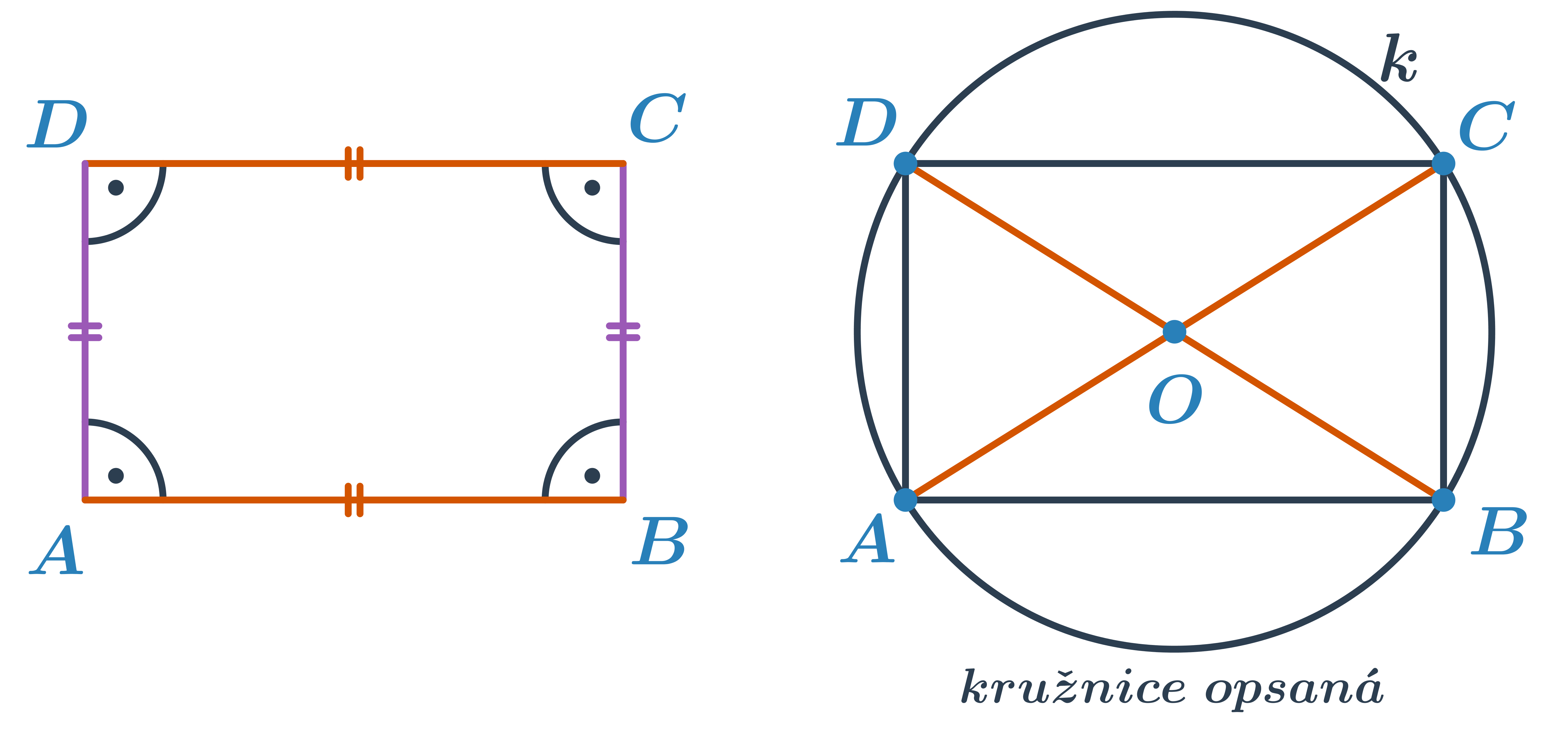
Při řešení konstrukčních úloh s obdélníky využíváme jejich následující vlastnosti:
- Všechny vnitřní úhly obdélníku jsou pravé, sousední strany jsou tedy na sebe kolmé.
- Protější strany jsou rovnoběžné.
- Všechny strany nemusí být stejně dlouhé. Stejně dlouhé jsou vždy dvě protější strany.
- Úhlopříčky obdélníku jsou stejně dlouhé a navzájem se půlí.
- Každému obdélníku lze opsat kružnici. Nazýváme ji kružnice opsaná, prochází vrcholy obdélníku a má střed v průsečíku úhlopříček.
Konstrukce čtverců
Čtverec můžeme považovat za zvláštní případ obdélníku (nebo rovnostranného rovnoběžníku). Stejně jako obdélník má všechny vnitřní úhly pravé, sousední strany jsou na sebe kolmé a protější strany čtverce jsou rovnoběžné. Úhlopříčky čtverce se protínají v bodě, který nazýváme střed čtverce. Čtverce mají všechny pěkné vlastnosti obdélníků a ještě některé speciální navíc:
- Všechny strany čtverce jsou stejně dlouhé.
- Úhlopříčky čtverce jsou stejně dlouhé, jsou na sebe kolmé, procházejí středem čtverce a navzájem se půlí.
- Každému čtverci lze opsat kružnici. Nazýváme ji kružnice opsaná, prochází vrcholy čtverce a má střed ve středu čtverce.
- Každému čtverci lze také vepsat kružnici. Nazýváme ji kružnice vepsaná, dotýká se stran čtverce a má střed ve středu čtverce.
Kromě interaktivního procvičování níže jsou k dispozici ještě pracovní listy k vytištění a rýsování na papíře:
NahoruKonstrukce čtyřúhelníků: rovnoběžníky
Konstrukce rovnoběžníků
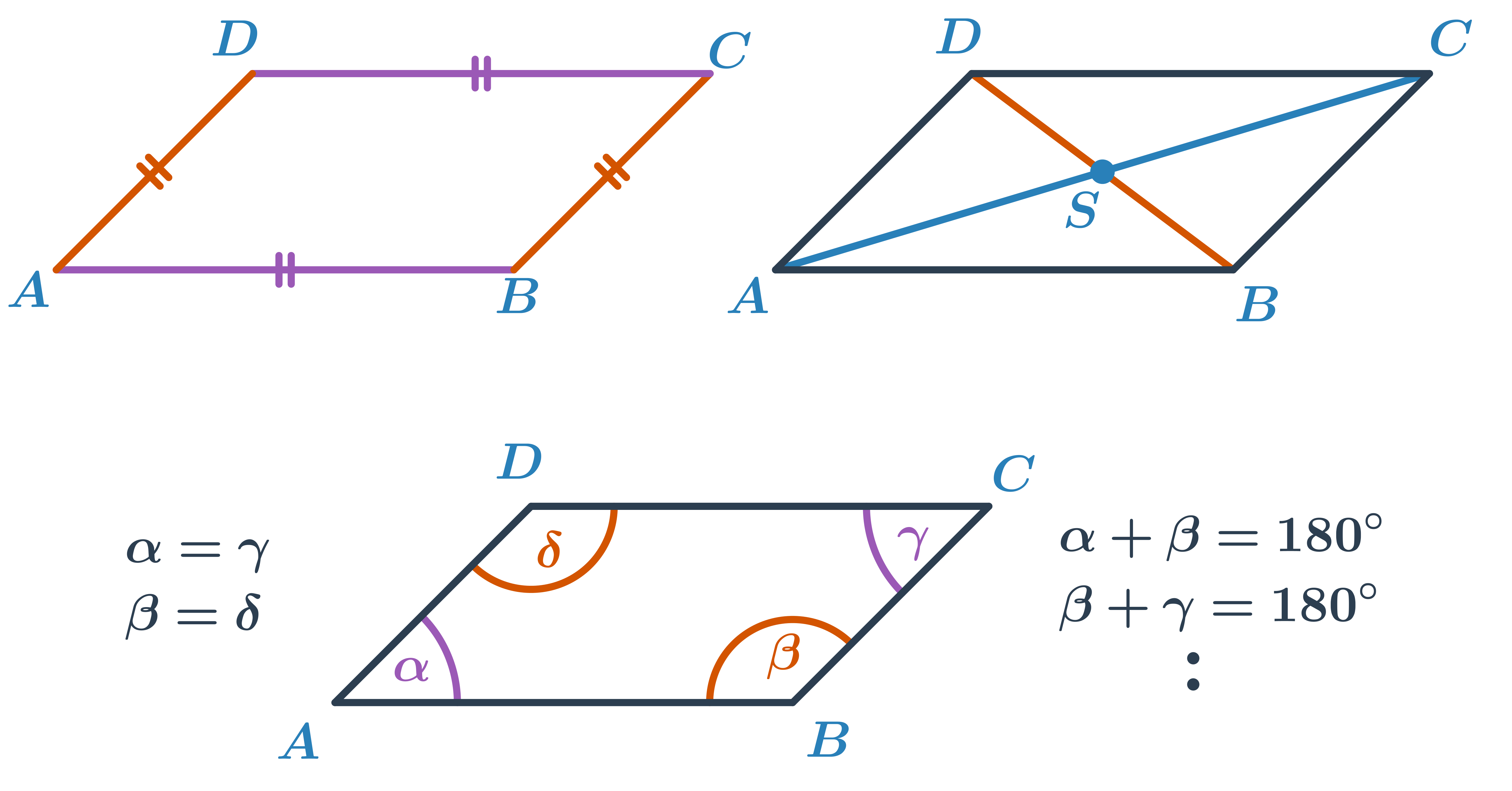
Rovnoběžník je speciální případ čtyřúhelníku, jehož protilehlé strany jsou rovnoběžné. Při řešení konstrukčních úloh využíváme následují vlastnosti rovnoběžníků:
- Protější strany jsou rovnoběžné.
- Všechny strany nemusí být stejně dlouhé. Stejně dlouhé jsou vždy dvě protější strany.
- Úhlopříčky rovnoběžníku nejsou stejně dlouhé, ale navzájem se půlí a protínají se ve středu rovnoběžníku.
- Každé dva protější úhly jsou stejné.
- Součet vnitřních úhlů u jedné strany je 180°.
Při konstrukci rovnoběžníku potřebujeme znát tři údaje, ze kterých jsem často schopni sestrojit některý trojúhelník určený podle vět s vrcholy ve trojici vrcholů rovnoběžníku. Zbývající vrchol rovnoběžníku pak najdeme pomocí rovnoběžek nebo shodnosti protějších stran.
Příklad: Sestrojte rovnoběžník ABCD, je-li dáno a=8 cm, b=5 cm, \beta=110^\circ.
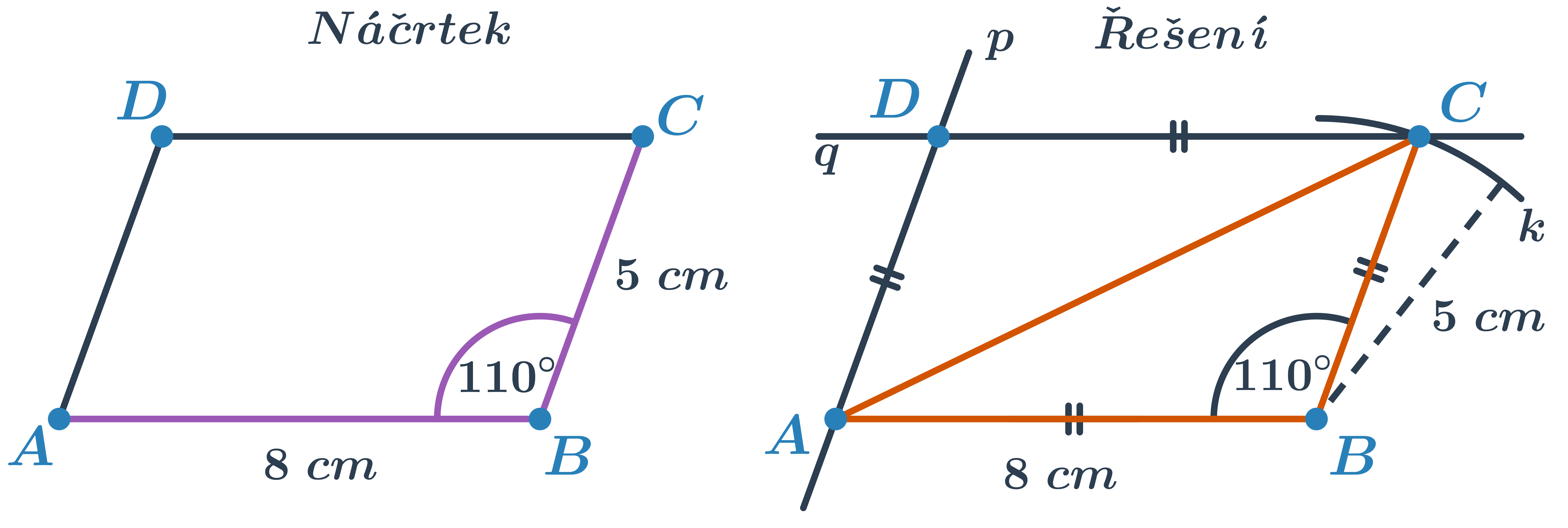
- Nejprve sestrojíme trojúhelník ABC určený podle věty sus.
- Pro konstrukci bodu D sestrojíme postupně ve vrcholech A a C rovnoběžky se stranami BC a AB.
Konstrukce kosočtverců
Kosočtverec je speciální případ rovnoběžníku. Má všechny strany stejně dlouhé. Proti obecnému rovnoběžníku mají jeho úhlopříčky navíc dvě speciální vlastnosti – jsou na sebe kolmé a půlí vnitřní úhly. Kosočtverci lze (stejně jako čtverci) vepsat kružnici.
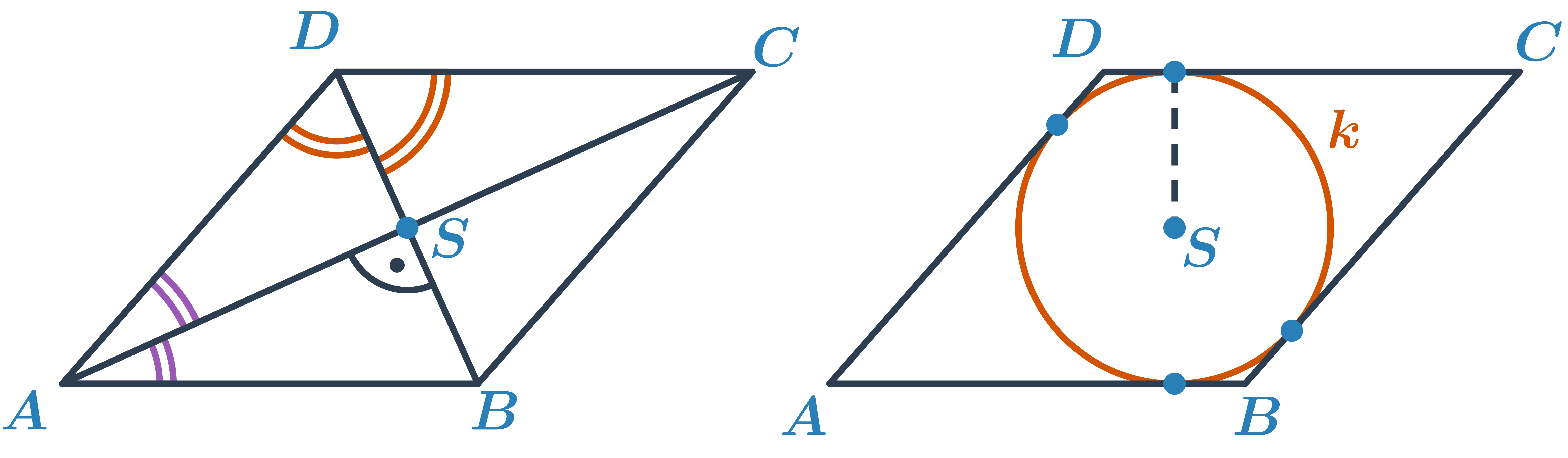
Kromě interaktivního procvičování níže je k dispozici ještě pracovní list k vytištění a rýsování na papíře:
NahoruKonstrukce čtyřúhelníků: lichoběžníky
Konstrukce lichoběžníků
Lichoběžník je čtyřúhelník, který má dvě rovnoběžné strany – ty se nazývají základny a dvě různoběžné strany – ramena. Vzdálenost základen se nazývá výška. Při konstrukcích budeme využívat následující vlastnosti:
- Základny jsou rovnoběžné.
- Úsečka spojující středy ramen se nazývá střední příčka a je rovnoběžná se základnami.
- Součet vnitřních úhlů u každého ramene je 180°.

Při konstrukci lichoběžníku potřebujeme znát čtyři údaje, ze kterých často dokážeme sestrojit trojúhelník určený podle vět s vrcholy ve třech vrcholech lichoběžníku. Zbývající vrchol lichoběžníku pak najdeme pomocí posledního údaje a rovnoběžnosti základen.
Příklad: konstrukce lichoběžníku, známé délky tří stran a úhlopříčky
Sestrojte lichoběžník ABCD, je-li dáno a=8 cm, b=6 cm, c=5 cm, |AC|=8 cm.
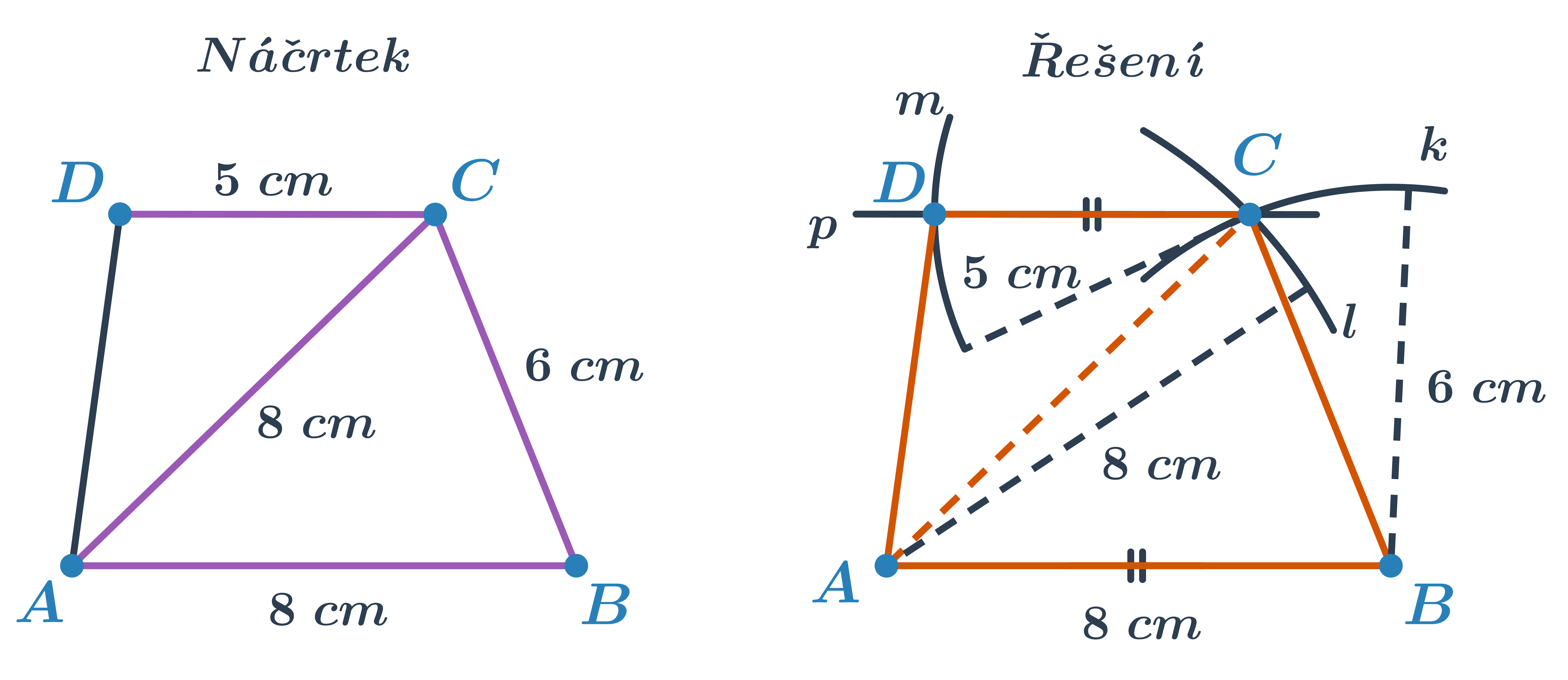
- Nejprve sestrojíme trojúhelník ABC určený podle věty sss.
- Základna CD je rovnoběžná se základnou AB. Bodem C tedy sestrojíme rovnoběžku p se stranou AB.
- Na tuto rovnoběžku pak naneseme délku strany c – poslední známý údaj.
Konstrukce rovnoramenných lichoběžníků
V rovnoramenném lichoběžníku mají obě ramena stejnou délku. Odpovídající vnitřní úhly u těchto ramen jsou pak stejné (dva stejné úhly \alpha = \beta u jedné základny a dva stejné úhly \gamma=\delta=180^\circ - \alpha u druhé základny). Úhlopříčky rovnoramenného lichoběžníku jsou stejně dlouhé. Narozdíl od obecného lichoběžníku mu lze opsat kružnici. Střed této opsané kružnice ale neleží v průsečíku úhlopříček.
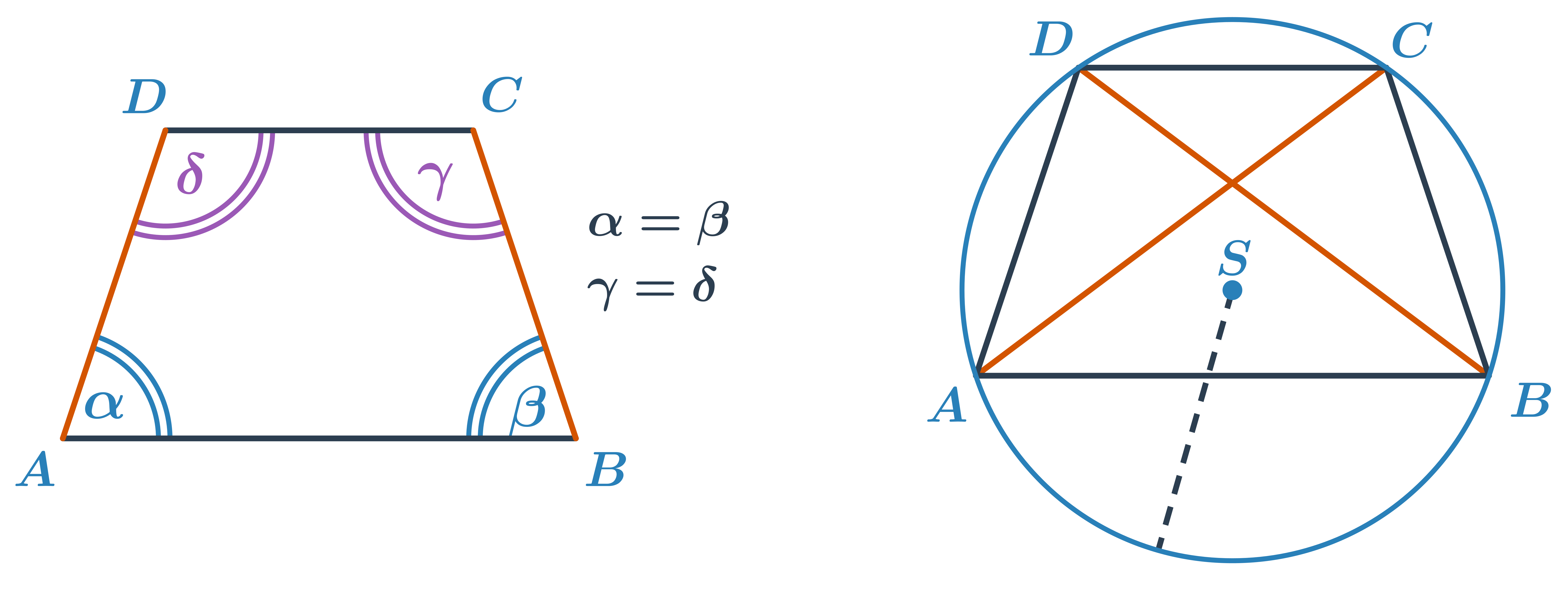
Kromě interaktivního procvičování níže je k dispozici ještě pracovní list k vytištění a rýsování na papíře:
NahoruKonstrukce obecných čtyřúhelníků
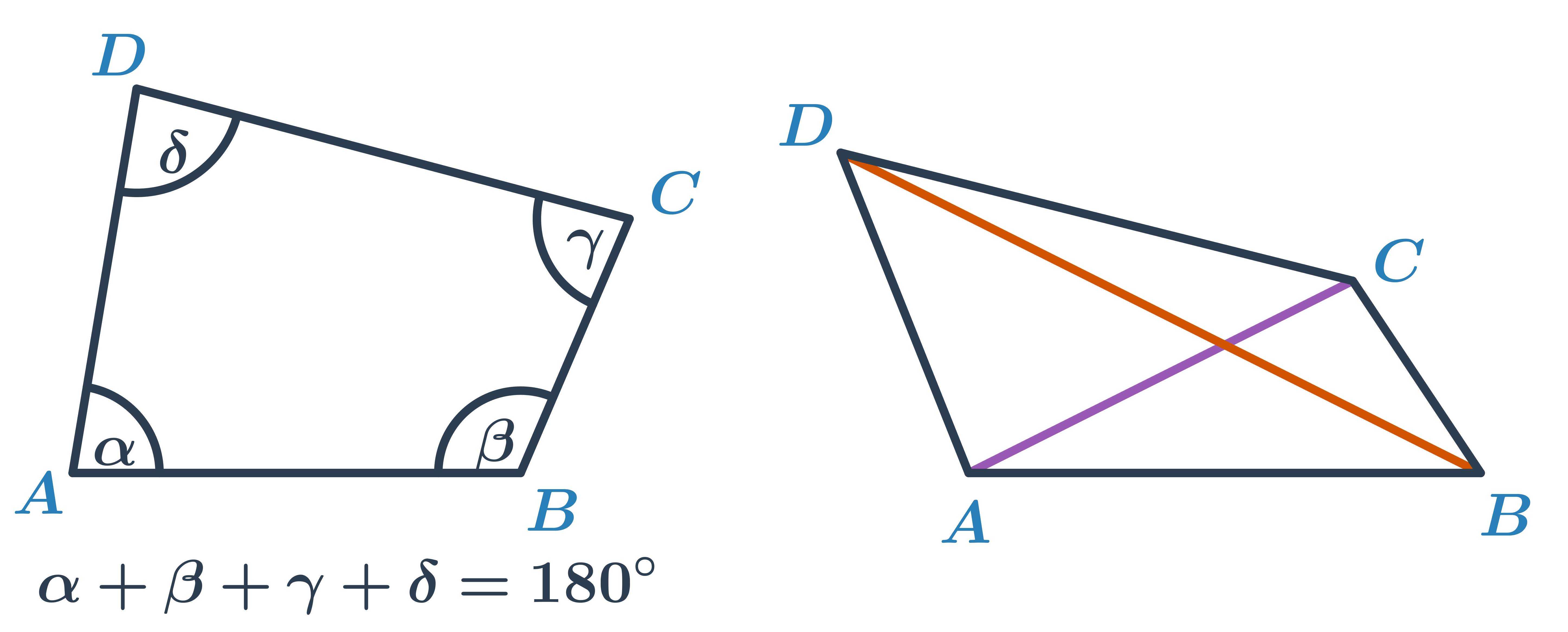
Víme, že čtyřúhelník je rovinný útvar ohraničený čtyřmi úsečkami, které spojují jeho vrcholy. Ve čtyřúhelníku může obecně být každá strana jinak dlouhá a každý vnitřní úhel může mít jinou velikost. Součet velikostí vnitřních úhlů je vždy 360^\circ. Pokud má čtyřúhelník všechny vnitřní úhly menší než 180^\circ, nazýváme ho konvexní. Speciálními případy konvexního čtyřúhelníku jsou čtverec, obdélník, rovnoběžník a lichoběžník. Pokud má čtyřúhelník jeden vnitřní úhel větší než 180^\circ, nazýváme ho nekonvexní.
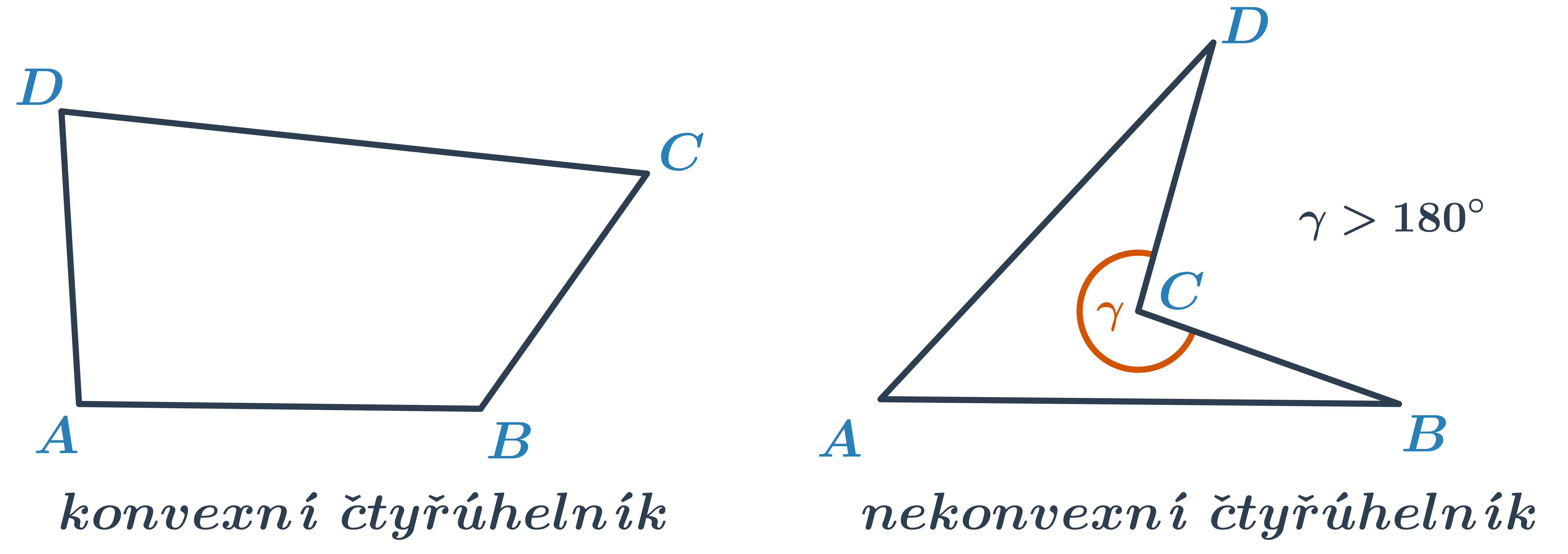
Úhlopříčky ve čtyřúhelníku mohou mít různou délku a rozdělují čtyřúhelník na dva trojúhelníky. Čtyřúhelník jako rovinný útvar si tak můžeme představit jako sjednocení dvou trojúhelníků. Toho často využijeme při konstrukci čtyřúhelníku, kdy jeden trojúhelník určený podle vět dokážeme sestrojit. Poslední vrchol pak doplníme pomocí zbývajících podmínek.
Příklad: konstrukce čtyřúhelníku, známé velikosti 3 stran a 2 úhlů
Sestrojte čtyřúhelník KLMN, je-li dáno |KL|=5 cm, |LM|=4 cm, |KN|=6 cm, |\sphericalangle NKL|=120^\circ,\ |\sphericalangle KLM|=100^\circ.
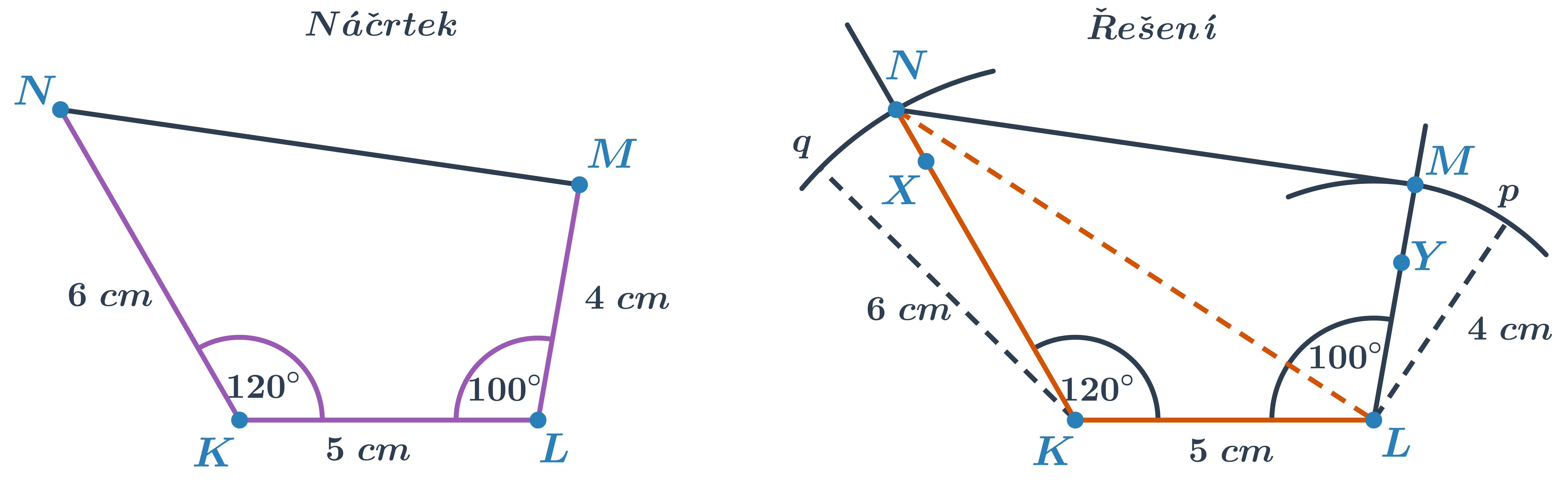
- Nejprve sestrojíme trojúhelník KLN určený podle věty sus.
- Dále sestrojíme úhel KLM pomocí polopřímky LY, která svírá s úsečkou KL úhel 100^\circ.
- Na polopřímku LY naneseme délku strany LM a dostaneme poslední vrchol M.
Kromě interaktivního procvičování níže je k dispozici ještě pracovní list k vytištění a rýsování na papíře:
Nahoru
