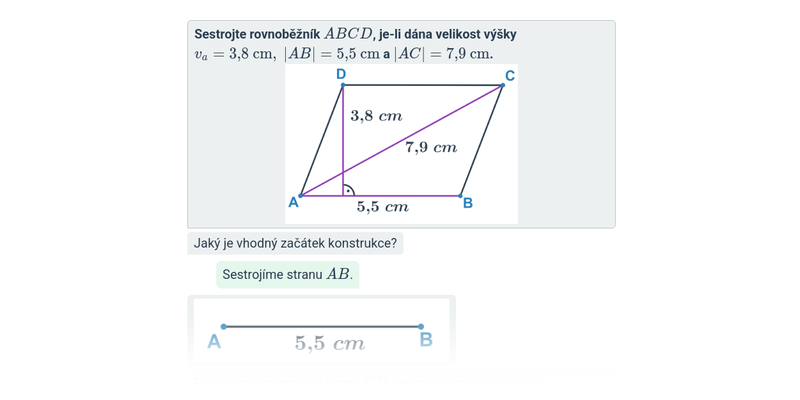
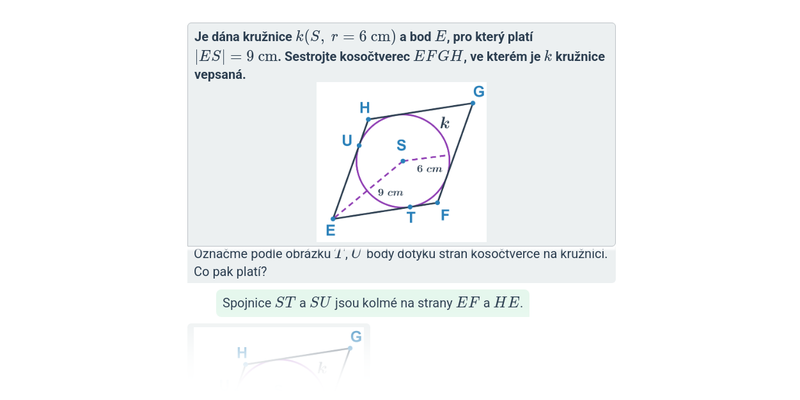
Konstrukce rovnoběžníků
Rovnoběžník je speciální případ čtyřúhelníku, jehož protilehlé strany jsou rovnoběžné. Při řešení konstrukčních úloh využíváme následují vlastnosti rovnoběžníků:
- Protější strany jsou rovnoběžné.
- Všechny strany nemusí být stejně dlouhé. Stejně dlouhé jsou vždy dvě protější strany.
- Úhlopříčky rovnoběžníku nejsou stejně dlouhé, ale navzájem se půlí a protínají se ve středu rovnoběžníku.
- Každé dva protější úhly jsou stejné.
- Součet vnitřních úhlů u jedné strany je 180°.
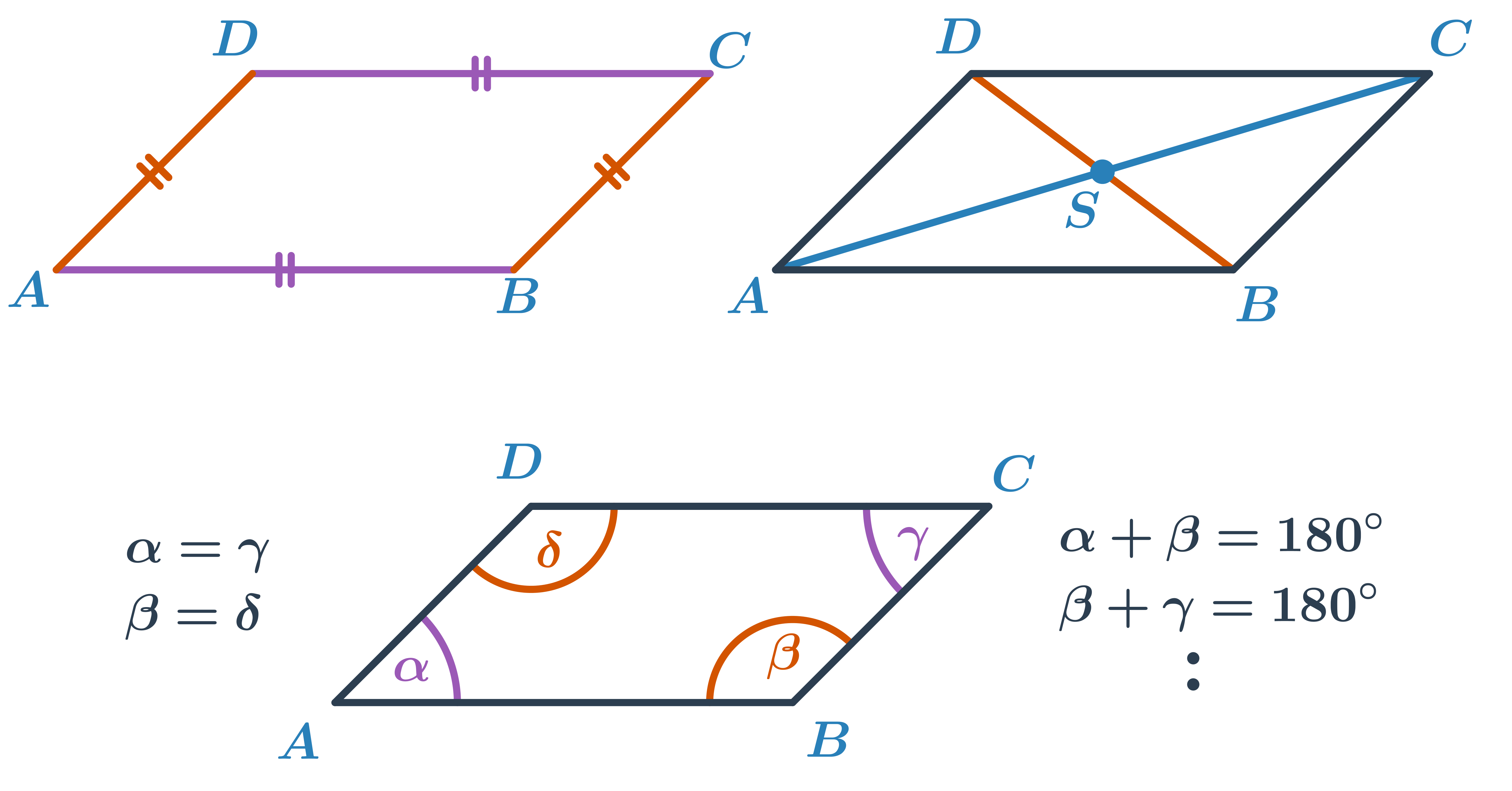
Při konstrukci rovnoběžníku potřebujeme znát tři údaje, ze kterých jsem často schopni sestrojit některý trojúhelník určený podle vět s vrcholy ve trojici vrcholů rovnoběžníku. Zbývající vrchol rovnoběžníku pak najdeme pomocí rovnoběžek nebo shodnosti protějších stran.
Příklad: Sestrojte rovnoběžník ABCD, je-li dáno a=8 cm, b=5 cm, \beta=110^\circ.
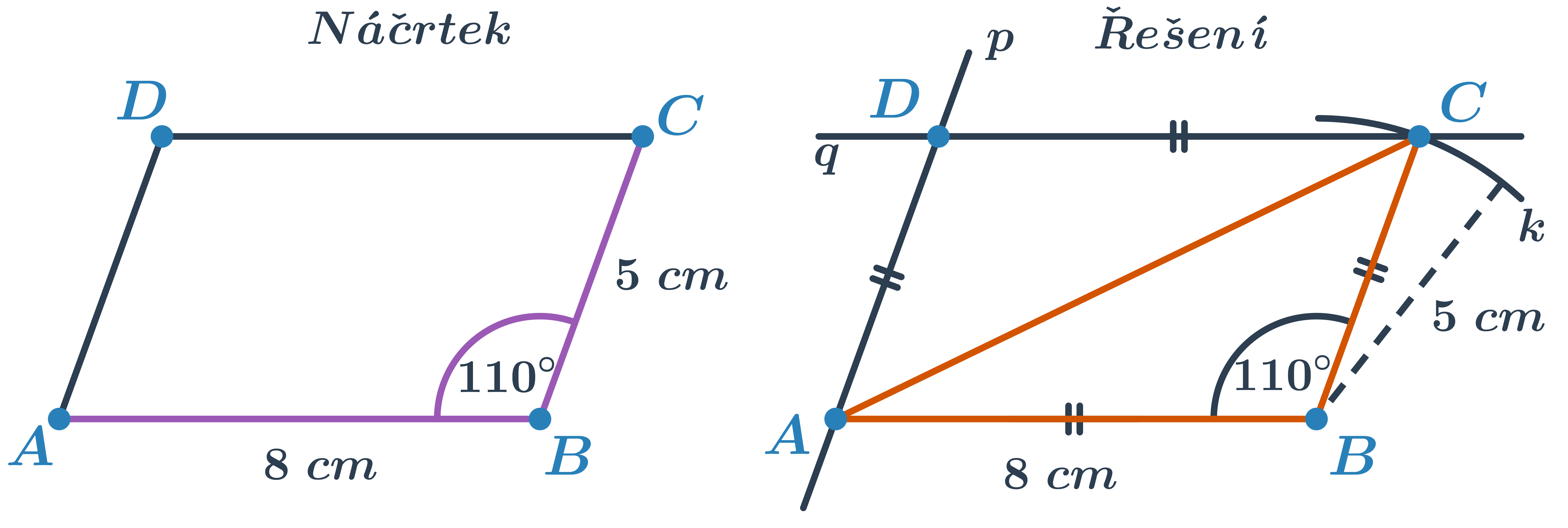
- Nejprve sestrojíme trojúhelník ABC určený podle věty sus.
- Pro konstrukci bodu D sestrojíme postupně ve vrcholech A a C rovnoběžky se stranami BC a AB.
Konstrukce kosočtverců
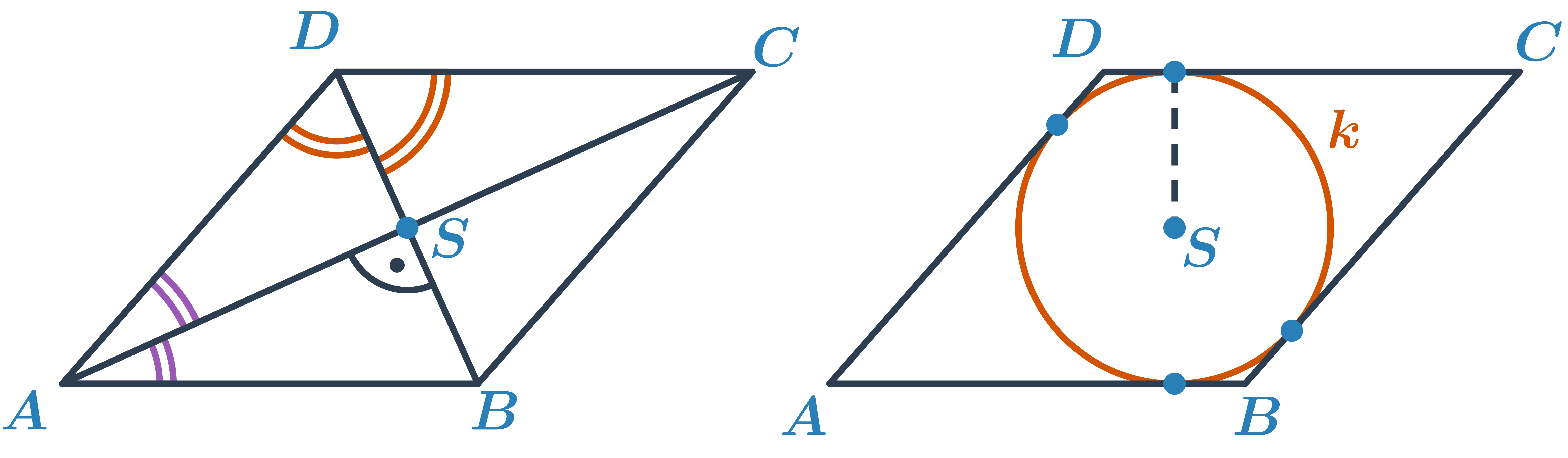
Kosočtverec je speciální případ rovnoběžníku. Má všechny strany stejně dlouhé. Proti obecnému rovnoběžníku mají jeho úhlopříčky navíc dvě speciální vlastnosti – jsou na sebe kolmé a půlí vnitřní úhly. Kosočtverci lze (stejně jako čtverci) vepsat kružnici.
Kromě interaktivního procvičování níže je k dispozici ještě pracovní list k vytištění a rýsování na papíře:
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.