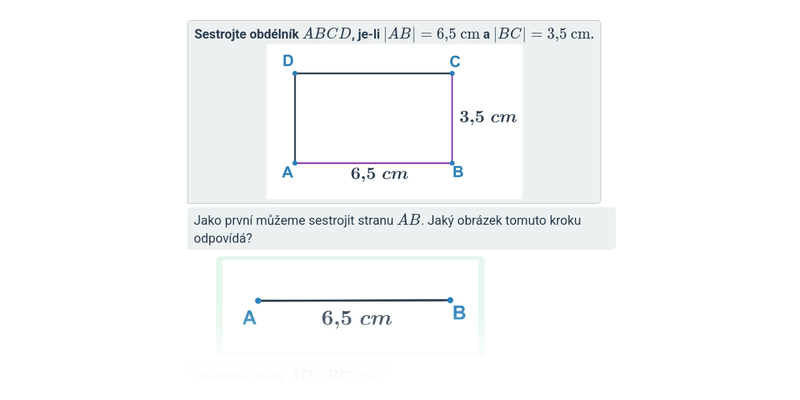
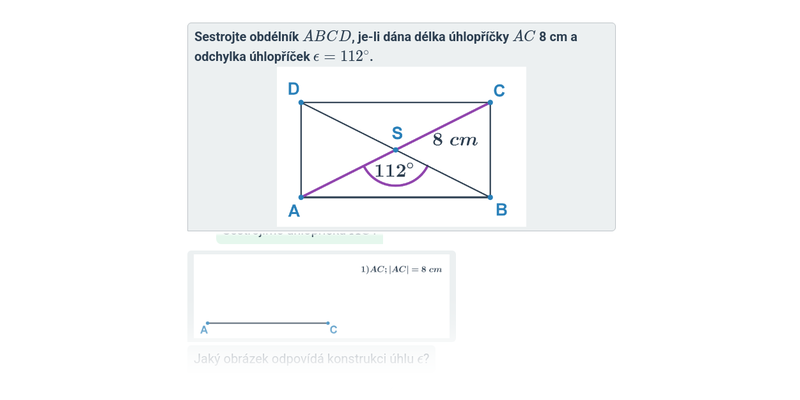
Konstrukce čtyřúhelníků: čtverce a obdélníky

Konstrukce obdélníků

Při řešení konstrukčních úloh s obdélníky využíváme jejich následující vlastnosti:

• Všechny vnitřní úhly obdélníku jsou pravé, sousední strany jsou tedy na sebe kolmé.
• Protější strany jsou rovnoběžné.
• Všechny strany nemusí být stejně dlouhé. Stejně dlouhé jsou vždy dvě protější strany.
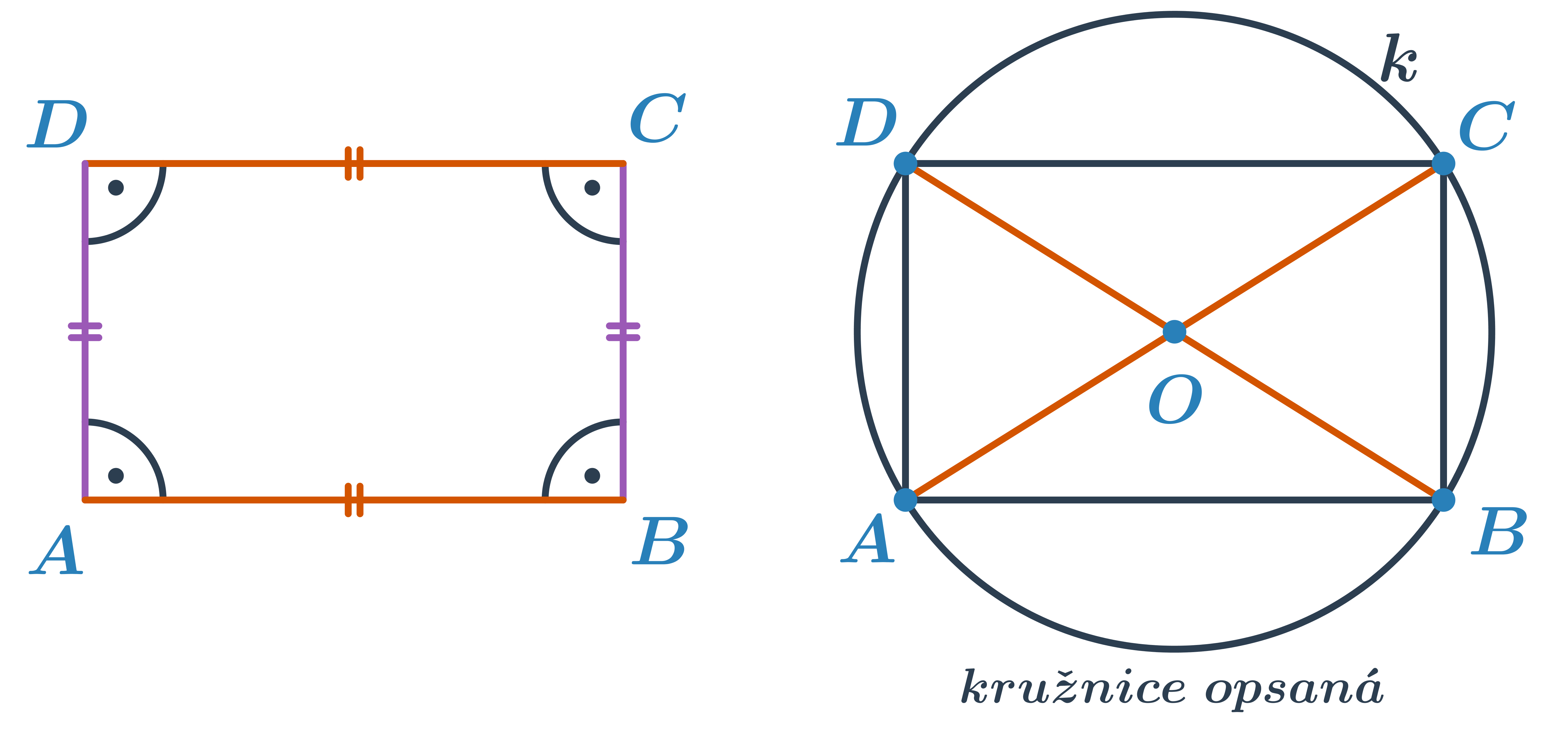
• Úhlopříčky obdélníku jsou stejně dlouhé a navzájem se půlí.
• Každému obdélníku lze opsat kružnici. Nazýváme ji kružnice opsaná, prochází vrcholy obdélníku a má střed v průsečíku úhlopříček.

Konstrukce čtverců

Čtverec můžeme považovat za zvláštní případ obdélníku (nebo rovnostranného rovnoběžníku). Stejně jako obdélník má všechny vnitřní úhly pravé, sousední strany jsou na sebe kolmé a protější strany čtverce jsou rovnoběžné. Úhlopříčky čtverce se protínají v bodě, který nazýváme střed čtverce. Čtverce mají všechny pěkné vlastnosti obdélníků a ještě některé speciální navíc:

• Všechny strany čtverce jsou stejně dlouhé.
• Úhlopříčky čtverce jsou stejně dlouhé, jsou na sebe kolmé, procházejí středem čtverce a navzájem se půlí.
• Každému čtverci lze opsat kružnici. Nazýváme ji kružnice opsaná, prochází vrcholy čtverce a má střed ve středu čtverce.
• Každému čtverci lze také vepsat kružnici. Nazýváme ji kružnice vepsaná, dotýká se stran čtverce a má střed ve středu čtverce.

Pracovní listy

Kromě interaktivního procvičování níže jsou k dispozici ještě pracovní listy k vytištění a rýsování na papíře:

Konstrukce čtverce a obdélníku (pro 4. ročník) řešení 🔒

Materiál je dostupný pouze uživatelům s platnou licencí pro daný předmět (učitelům nebo členům rodiny).

Konstrukce čtyřúhelníků: čtverce a obdélníky řešení 🔒

Materiál je dostupný pouze uživatelům s platnou licencí pro daný předmět (učitelům nebo členům rodiny).