Výpis souhrnů
Geometrické konstrukce
Podtémata
- Geometrické konstrukce
- Geometrické konstrukce: značení
- Polopřímky a poloroviny
- Rovnoběžky a kolmice
- Konstrukční úlohy: trojúhelníky
- Konstrukce trojúhelníků: známé délky stran
- Konstrukce trojúhelníků: rovnoramenné a rovnostranné trojúhelníky
- Konstrukce trojúhelníků: věty sss, sus, usu, Ssu
- Konstrukce trojúhelníků: těžnice, výšky, vepsaná a opsaná kružnice
- Konstrukční úlohy: čtyřúhelníky
- Konstrukce čtyřúhelníků: čtverce a obdélníky
- Konstrukce čtyřúhelníků: rovnoběžníky
- Konstrukce čtyřúhelníků: lichoběžníky
- Konstrukce obecných čtyřúhelníků
- Konstrukční úlohy průřezově
Geometrické konstrukce
Konstrukční úlohou rozumíme úlohu, ve které chceme sestrojit určitý geometrický útvar (alespoň jeden, případně všechny) splňující dané podmínky. Jinými slovy, pomocí pravítka, kružítka a případně i úhloměru sestrojíme geometrický útvar (trojúhelník, obdélník atd.), pro který známe délky jeho stran, velikosti úhlů či jiné vlastnosti.
Před rýsováním je dobré si ujasnit:
- body značíme velkými písmeny, např bod A
- přímky značíme malými písmeny, např. přímka p
Obvyklé kroky řešení konstrukční úlohy
Náčrtek: Od ruky si nakreslíme obrázek hledaného útvaru se vším, co známe ze zadání. To nám pomůže představit si výsledek. Pro přehlednost můžeme jednotlivé prvky vyznačit barevně. Nezapomeňte, náčrtky děláme velké a přehledné. V obrázku velkém jako blecha nic neuvidíme.
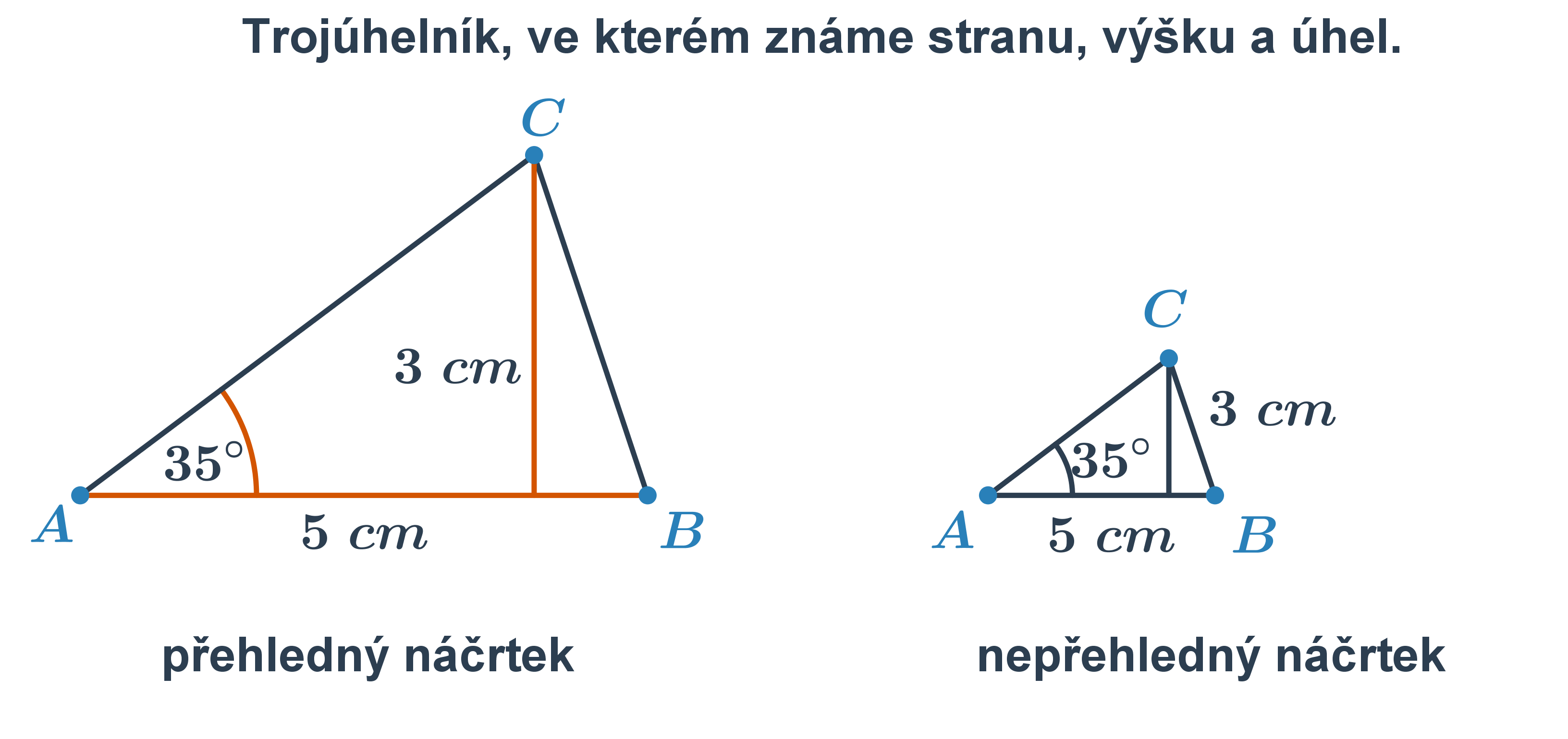
Popis konstrukce: Popis jednotlivých kroků, které musíme udělat, abychom dospěli k výsledku. Popis píšeme proto, aby každý mohl náš postup zopakovat. Z výsledného obrázku to nejde vždy snadno udělat. Pro zápis konstrukce používáme geometrické značení. Popis konstrukce řešíme obvykle až ve vyšších ročnících.
Konstrukce: Jde o samotné rýsování příkladu.
Zkouška správnosti: Měli bychom ověřit, jestli obrázek opravdu splňuje všechny podmínky ze zadání.
Počet řešení (diskuse): Zjistíme počet výsledků, které vyhovují zadání úlohy. Ne vždy musíme všechny výsledky narýsovat. Například při konstrukci trojúhelníku se známými délkami stran nám typicky stačí narýsovat jeden trojúhelník „nad“ první narýsovanou stranou, i když oblouky mají dva průsečíky a mohly by nám vzniknout dva shodné trojúhelníky. U dalších jednodušších úloh většinou postupujeme podobně. Při řešení náročnějších konstrukčních úloh, kde je vyžadováno nalezení všech řešení, je dobré mít na paměti, v kolika bodech se útvary doopravdy protínají a zda uvažujeme skutečně celé množiny bodů daných vlastností.
Pracovní listy
Kromě níže uvedených interaktivních cvičení jsou k dispozici také následující pracovní listy k vytištění a rýsování na papíře:
- Konstrukce čtverce a obdélníku (pro 4. ročník) + řešení
- Konstrukce trojúhelníků: známé délky stran + řešení
- Konstrukce rovnostranných a rovnoramenných trojúhelníků + řešení
- Konstrukce trojúhelníků podle vět + řešení
- Konstrukce trojúhelníků: těžnice, výšky + řešení
- Konstrukce trojúhelníků: vepsaná a opsaná kružnice + řešení
- Konstrukce čtyřúhelníků: čtverce a obdélníky + řešení
- Konstrukce čtyřúhelníků: rovnoběžníky a lichoběžníky + řešení
- Konstrukce čtyřúhelníků: obecný čtyřúhelník + řešení
- Konstrukce s použitím osové souměrnosti + řešení
- Konstrukce s použitím středové souměrnosti + řešení
- Konstrukční úlohy: průřezově (pro 9. ročník) + řešení
Geometrické konstrukce: značení
| Značka | Význam |
|---|---|
| p \parallel q | rovnoběžné přímky |
| p \perp q | kolmé přímky |
| \sphericalangle BAC | úhel při vrcholu A |
| \triangle ABC | trojúhelník ABC |
| \vert AB\vert | délka úsečky AB |
| A \in p | A leží na přímce p |
| A \notin p | A neleží na přímce p |
| \leftrightarrow AB | přímka procházející body A, B |
| \mapsto AB | polopřímka začínající v bodě A, procházející bodem B |
| \mapsto ABC | polorovina s hraniční přímkou AB, obsahující bod C |
| \mapsto pK | polorovina s hraniční přímkou p, obsahující bod K |
| \leftrightarrow ABC | rovina určená body A, B, C |
| (p, q) | pás roviny, ohraničený rovnoběžkami p, q |
Dále využíváme pro zápis geometrických konstrukcí množinové operace, především průnik (\cap) a sjednocení (\cup).
NahoruPolopřímky a poloroviny
Polopřímka je část přímky, která vznikne rozdělením přímky jedním jejím bodem. Tento bod se nazývá počáteční. Polopřímku s počátečním bodem A procházející bodem B značíme \mapsto AB. Každý bod rozděluje přímku na dvě opačné polopřímky se společným počátečním bodem.
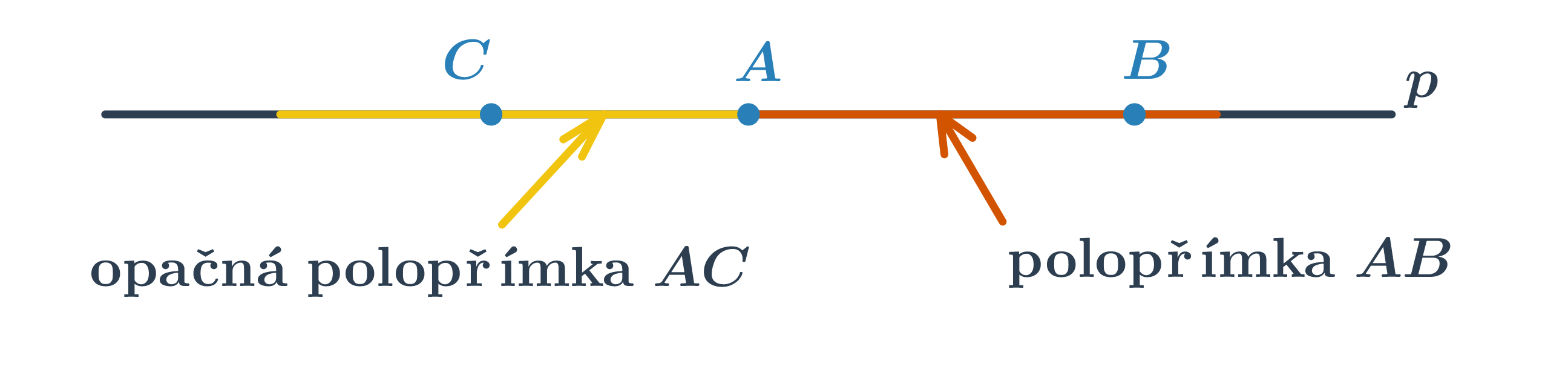
Základní vlastnosti polopřímek:
- Sjednocením dvou opačných polopřímek je přímka.
- Průnikem dvou opačných polopřímek je bod.
- Průnikem polopřímek \mapsto AB a \mapsto BA je úsečka AB.
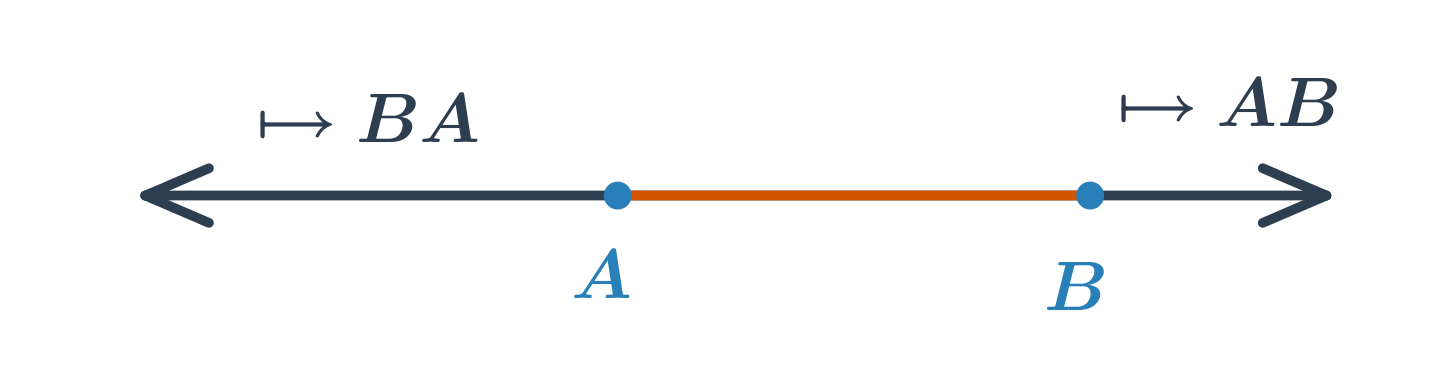
Polorovina je část roviny, která vznikne rozdělením roviny jednou přímkou. Tato přímka se nazývá hraniční. Polorovinu s hraniční přímkou p procházející bodem K značíme \mapsto pK. Je-li přímka p určena body A, B, můžeme také psát \mapsto ABK. Každá přímka rozděluje rovinu na dvě opačné poloroviny se společnou hraniční přímkou.
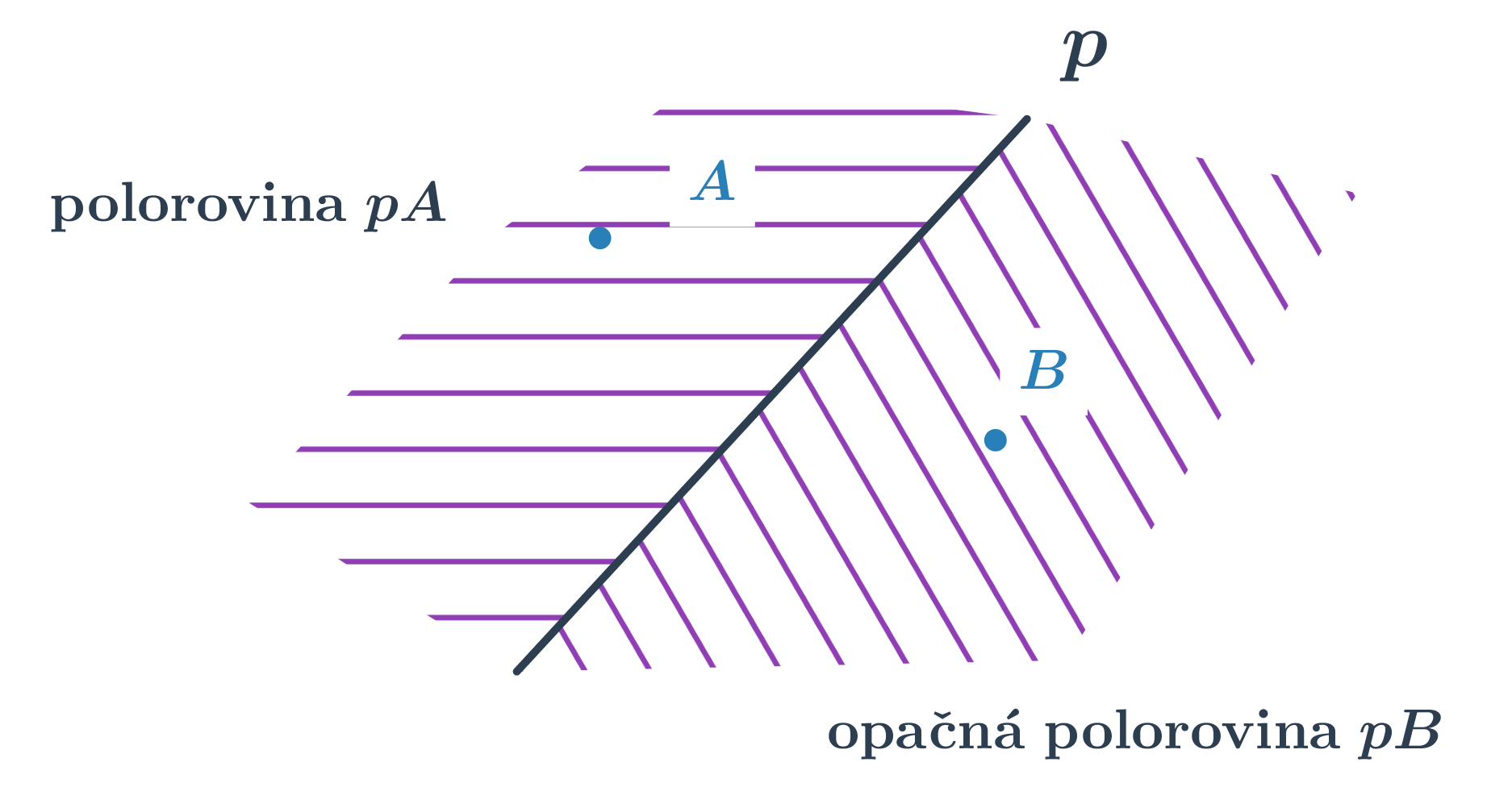
Základní vlastnosti polorovin:
- Sjednocením dvou opačných polorovin je rovina.
- Průnikem dvou opačných polorovin je hraniční přímka.
- Průnikem dvou polorovin s rovnoběžnými hraničními přímkami je pás rovnoběžek.
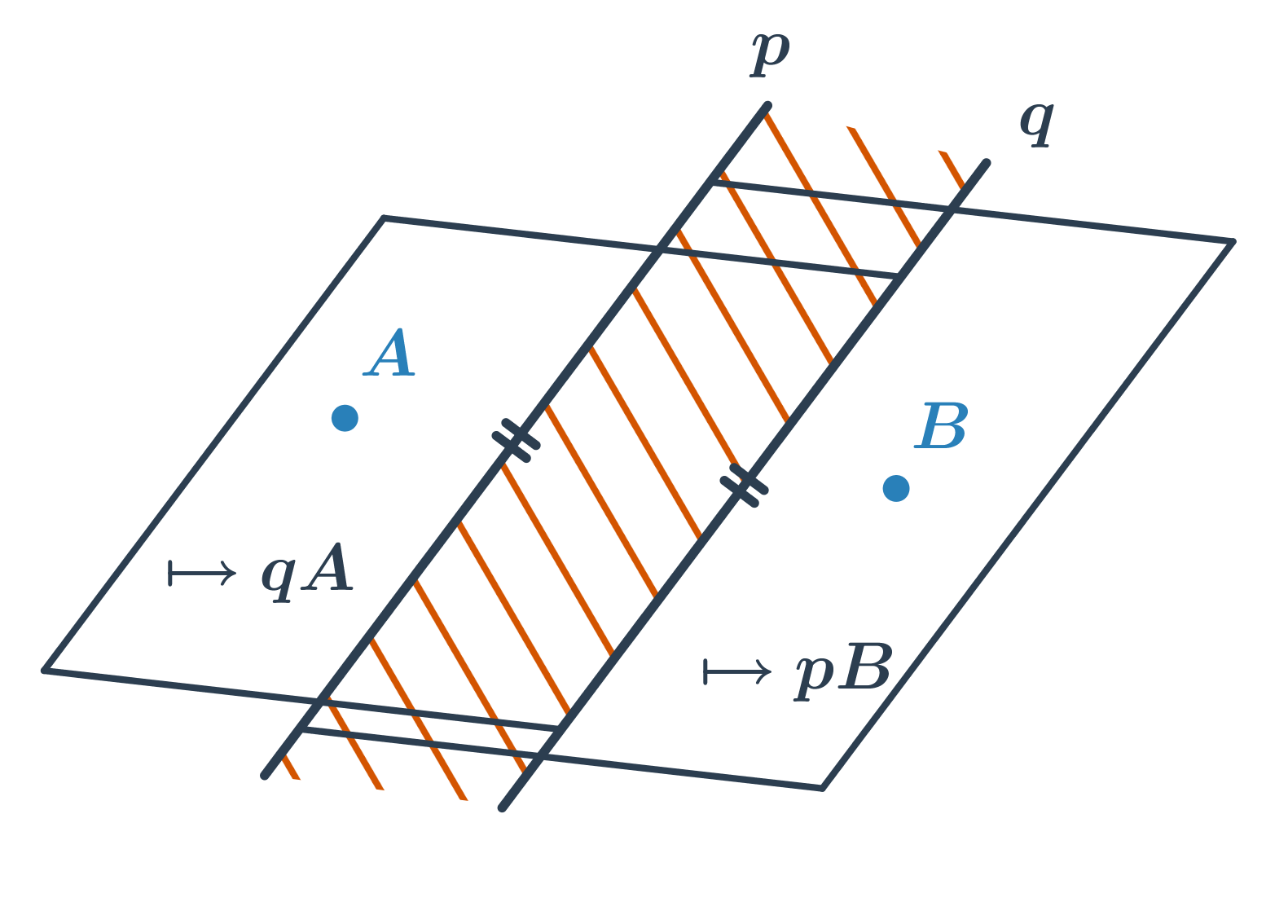
Pro zápis geometrických konstrukcí používáme množinové operace, především průnik \cap a sjednocení \cup.
Příklad: průnik přímky a poloroviny
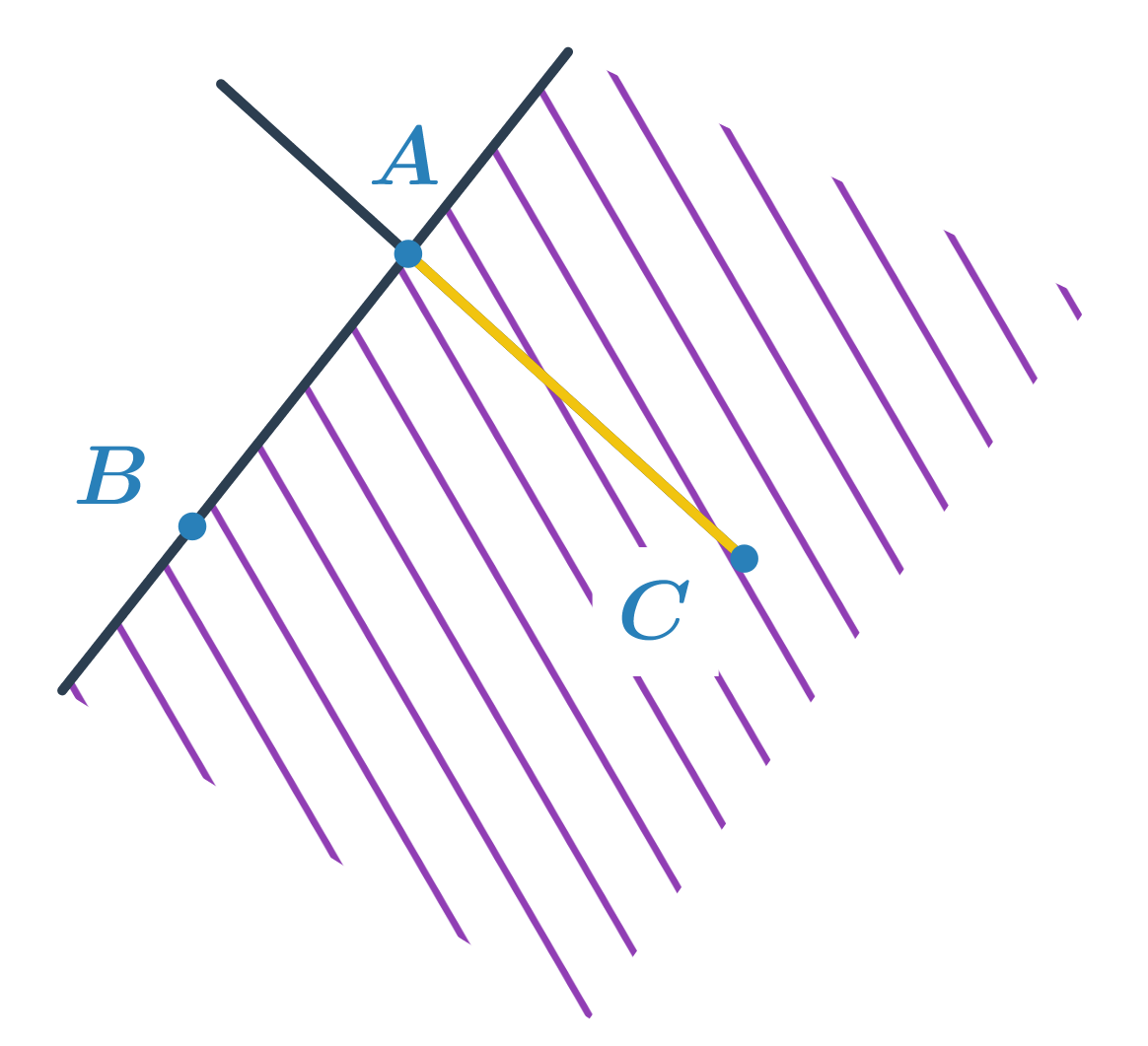
Rozhodněte, co je průnikem polopřímky CA a poloroviny ABC.
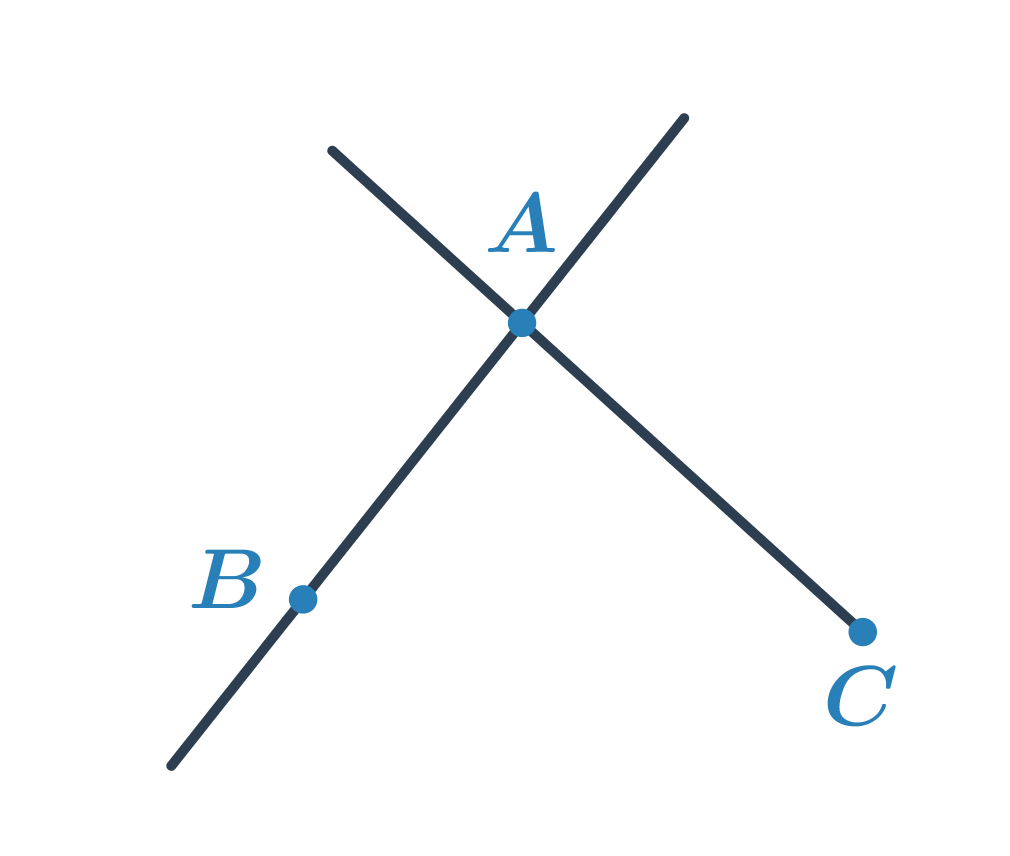
Polorovina ABC je určena hraniční přímkou AB a bodem C. Polopřímka CA má počáteční bod C a prochází bodem A. Průnikem je pak úsečka AC. Matematicky bychom úlohu zapsali: AC = \mapsto ABC \cap \mapsto CA.
Rovnoběžky a kolmice
Rovnoběžky jsou dvě přímky ležící ve stejné rovině, které se nikde neprotínají. Rovnoběžnost přímek p a q zapisujeme p \parallel q.
Kolmice je přímka, která protíná jinou přímku a svírá s ní úhel 90°. Kolmost přímek p a q zapisujeme p \perp q.
Dvě přímky, které jsou kolmé na nějakou třetí přímku a současně obě leží v jedné rovině, jsou rovnoběžky.
Komiks pro zpestření
Konstrukční úlohy: trojúhelníky
Při řešení jednodušších úloh provádíme konstrukce trojúhelníků se známými délkami stran. Nesmíme přitom zapomínat, že platí tzv. trojúhelníková nerovnost, tedy že součet dvou stran je větší než třetí strana. Jednoduše řečeno, jedině pokud je součet dvou nejkratších stran větší než třetí strana, trojúhelník lze sestrojit.
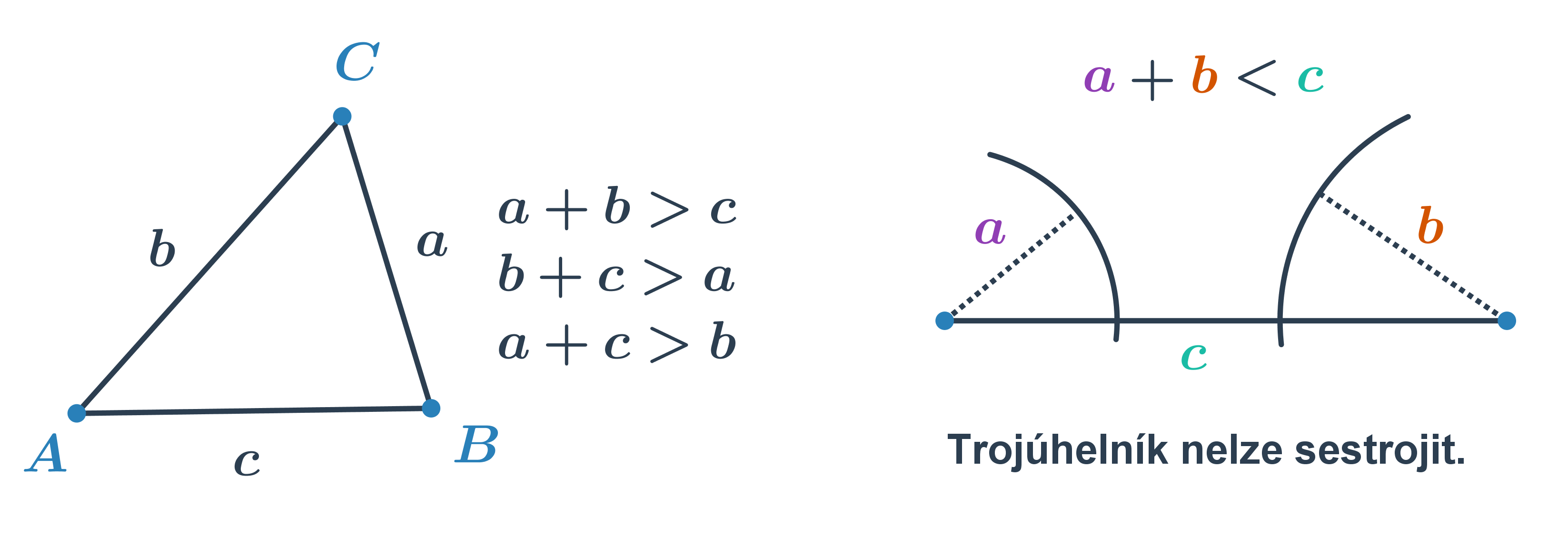
Občas má některý trojúhelník zajímavou vlastnost, která nám pomůže odvodit si potřebné informace k jeho sestrojení — může jít např. o konstrukci rovnoramenného nebo rovnostranného trojúhelníku.
Při řešení složitějších příkladů provádíme konstrukci trojúhelníků podle vět sss, sus, usu, Ssu, využíváme přitom známé věty o sestrojitelnosti trojúhelníků.
U nejtěžších příkladů, jako je konstrukce trojúhelníků, kdy známé údaje zahrnují těžnice, výšky, opsanou nebo vepsanou kružnici trojúhelníka využíváme při konstrukci další pojmy související s trojúhelníkem, či množiny bodů daných vlastností.
NahoruKonstrukce trojúhelníků: známé délky stran
Při konstrukci trojúhelníků můžeme každou stranu označit dvěma způsoby:
- přímo – strana a
- pomocí vrcholů – strana BC
Při konstrukcích také můžeme zaměňovat označení strany a její délky. Můžeme psát a=|BC|. Je třeba myslet i na pravidlo, že strana je pojmenovaná podle protějšího vrcholu.
Příklad: Je v trojúhelníku na obrázku délka strany a=8 cm?
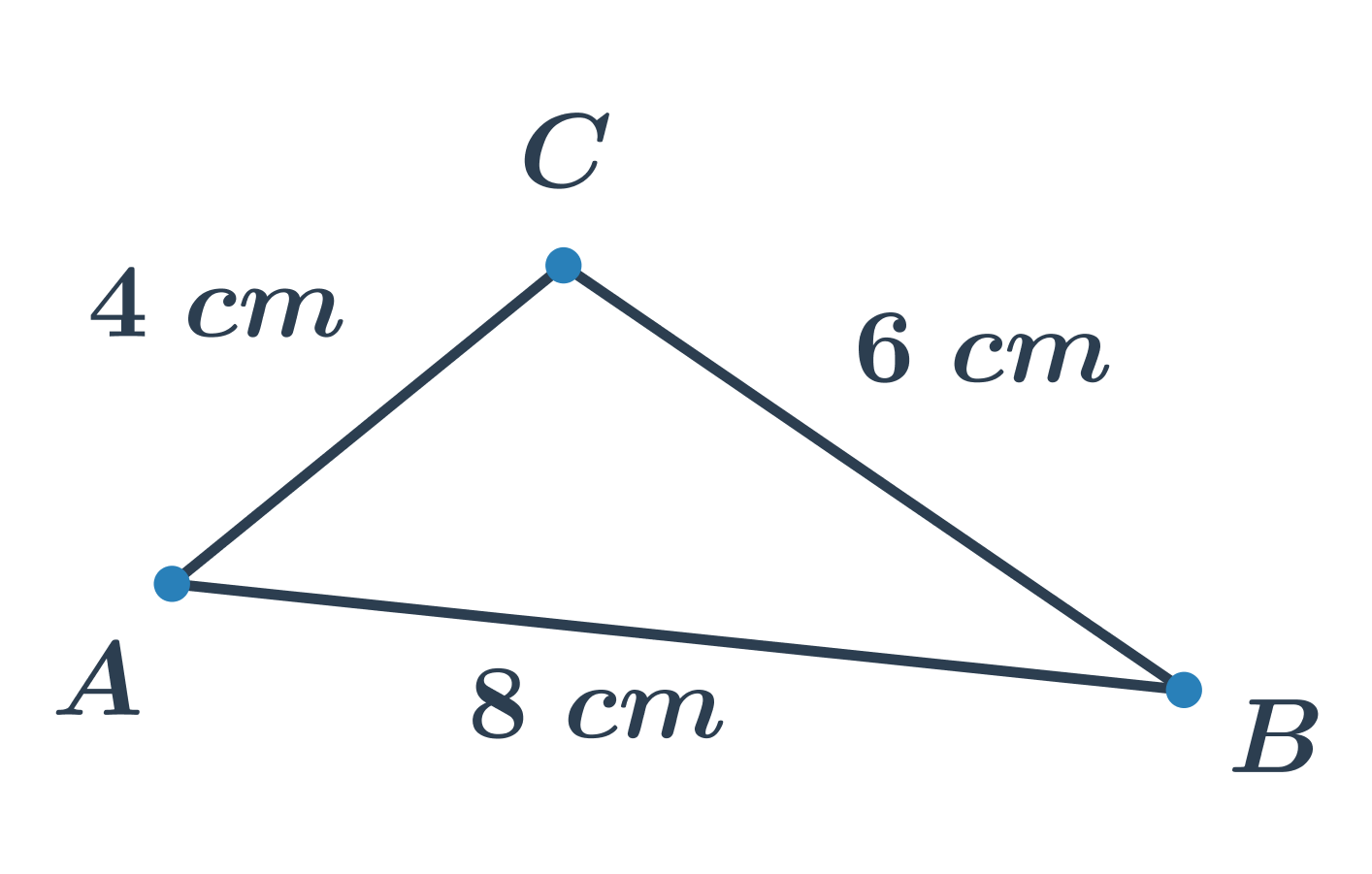
- Strana a leží proti vrcholu A. Je to tedy strana BC.
- Z obrázku vidíme, že |BC|=6 cm.
- Strana a tedy nemá délku 8 cm.
- Délku 8 cm má v tomto trojúhelníku strana AB, tedy strana c.
Lze sestrojit trojúhelník se stranami zadané délky?
- 6\ \text{cm}, 5\ \text{cm}, 4\ \text{cm} - součet dvou nejkratších stran je 4 + 5= 9 \ \text{cm}, to je více než 6\ \text{cm}, takže je splněna trojúhelníková nerovnost a trojúhelník lze sestrojit.
- 6\ \text{cm}, 5\ \text{cm}, 1\ \text{cm} - součet dvou nejkratších stran je 1 + 5 = 6\ \text{cm}, to je rovno délce třetí strany, takže není splněna trojúhelníková nerovnost a trojúhelník nelze sestrojit.
- 5\ \text{cm}, 2\ \text{cm}, 1\ \text{cm} - součet dvou nejkratších stran je 1 + 2 = 3\ \text{cm}, to je menší než délka třetí strany 5\ \text{cm}, takže není splněna trojúhelníková nerovnost a trojúhelník nelze sestrojit.
- 7\ \text{cm}, 7\ \text{cm}, 7\ \text{cm} - součet dvou nejkratších stran je 7 + 7= 14\ \text{cm}, to je více než 7\ \text{cm}, takže je splněna trojúhelníková nerovnost a trojúhelník lze sestrojit.
Při konstrukcích trojúhelníků, u kterých známe tři strany, postupujeme tak, že sestrojíme jako první libovolnou stranu, na obrázku například AB. K nalezení posledního vrcholu C použijeme dvě kružnice nebo jejich části. Výsledkem konstrukce jsou dva shodné (stejné) trojúhelníky, proto stačí sestrojit jen jeden.
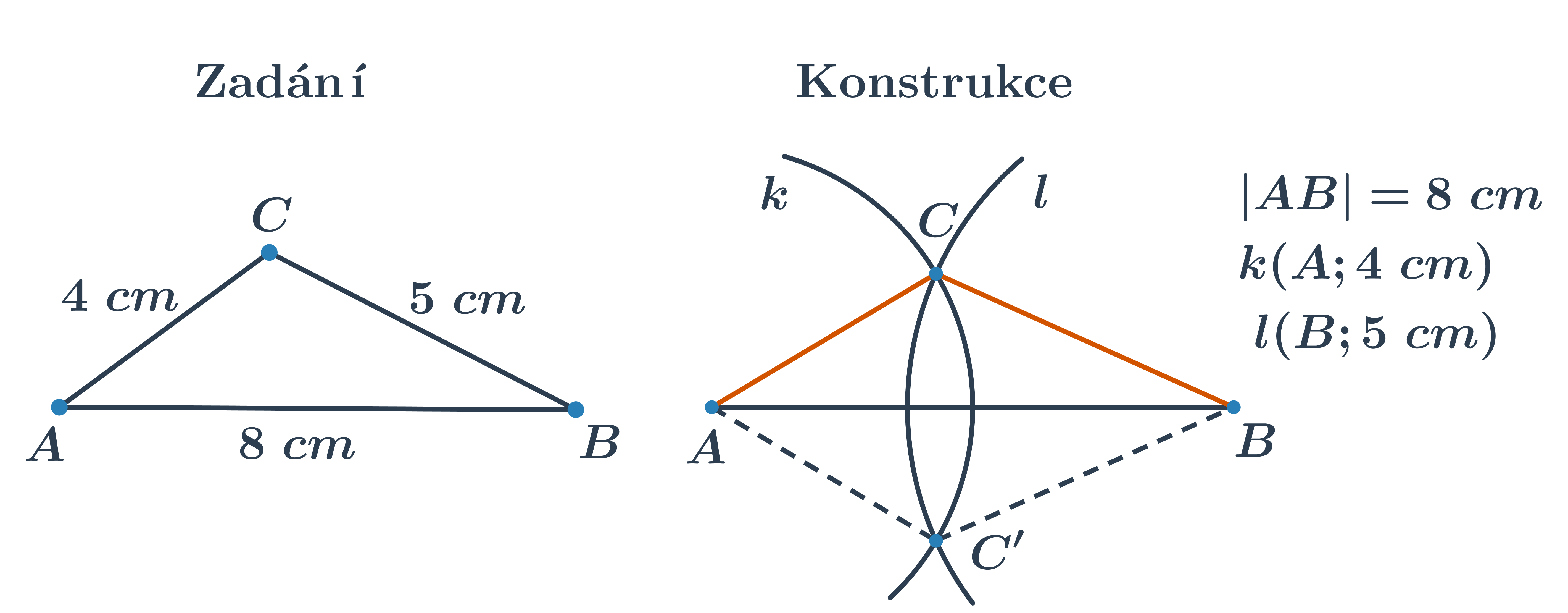
Kromě níže uvedených interaktivních cvičení je k dispozici také pracovní list k vytištění a rýsování na papíře:
NahoruKonstrukce trojúhelníků: rovnoramenné a rovnostranné trojúhelníky
Při konstrukci rovnoramenného trojúhelníku využíváme jeho základní vlastnosti:
- Má dvě strany (ramena) shodné. Vrchol proti základně tedy leží na ose základny.
- Shodné (stejně velké) jsou i vnitřní úhly při základně.
- Výška kolmá na základnu leží na ose základny a dělí rovnoramenný trojúhelník na dva shodné trojúhelníky.
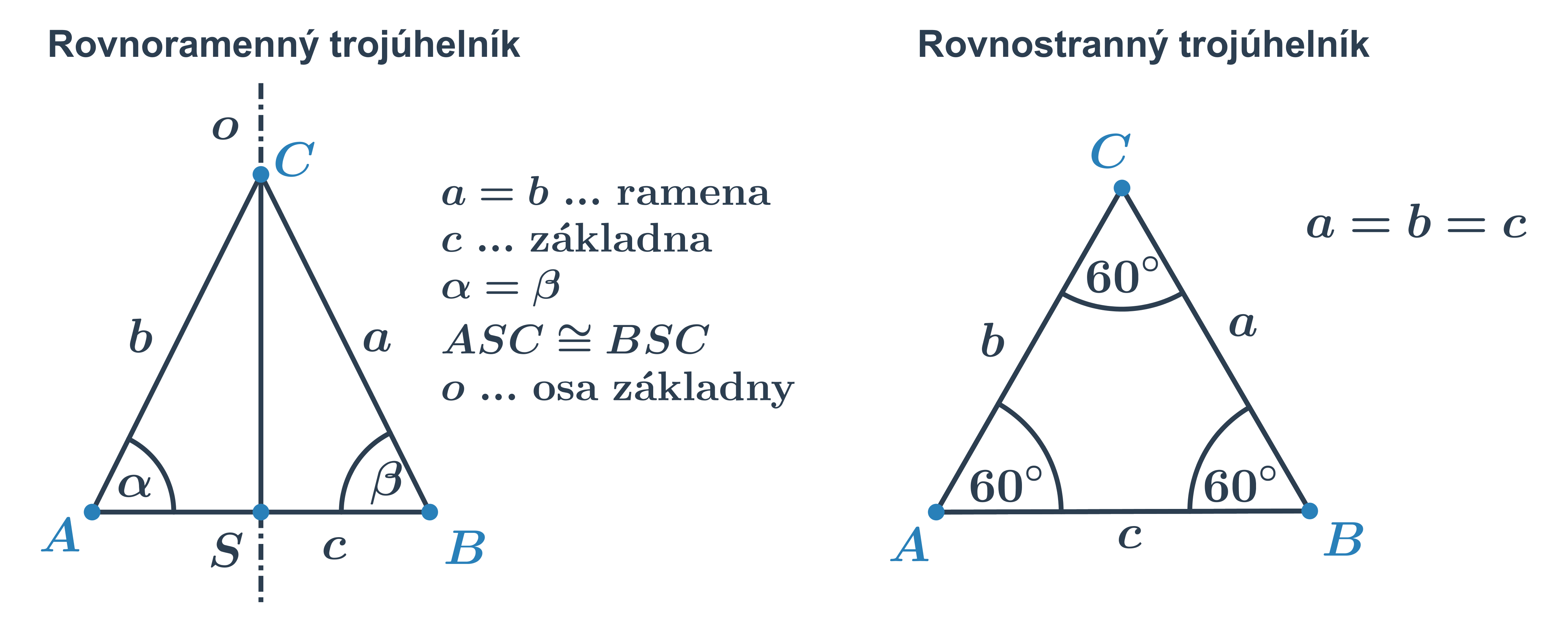
Rovnostranný trojúhelník můžeme chápat jako speciální případ rovnoramenného trojúhelníka. Má všechny strany stejně dlouhé a velikost všech jeho vnitřních úhlů je 60°.
Kromě níže uvedených interaktivních cvičení je k dispozici také pracovní list k vytištění a rýsování na papíře:
NahoruKonstrukce trojúhelníků: věty sss, sus, usu, Ssu
Při složitějších příkladech využíváme věty o sestrojitelnosti trojúhelníků (kde s značí stranu a u úhel):
- Věta sss — v trojúhelníku jsou dány délky všech stran, pro které platí trojúhelníková nerovnost.
- Věta sus— v trojúhelníku jsou dány délky dvou stran a velikost úhlu, který svírají (menší než 180°).
- Věta usu — v trojúhelníku je dána délka jedné strany a velikosti 2 úhly k ní přiléhající (součet velikostí daných úhlů je menší než 180°).
- Věta Ssu — známe velikosti dvou stran trojúhelníka a velikost úhlu proti větší z těchto stran (velikost zadaného úhlu je menší než 180°).
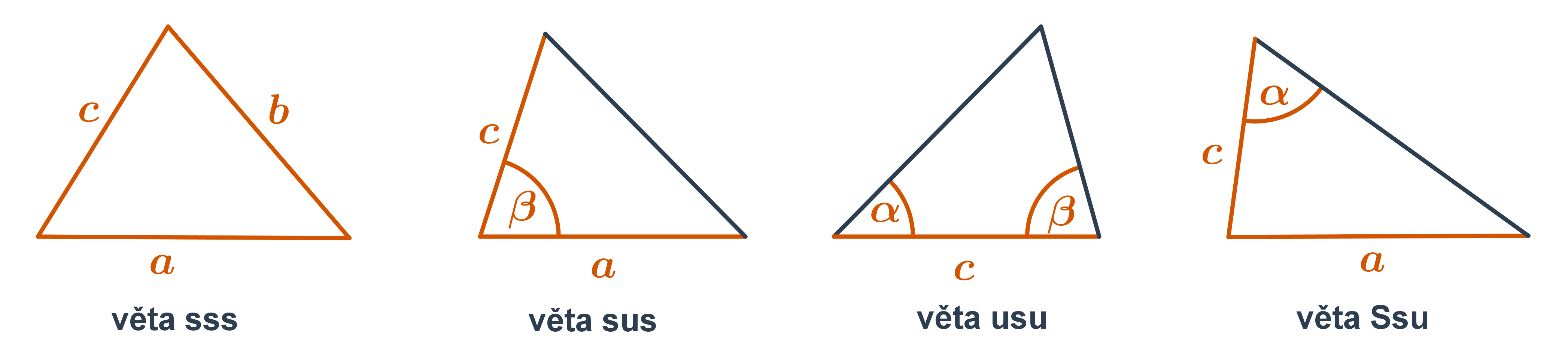
Tyto věty také používáme při určení shodnosti trojúhelníků.
Kromě níže uvedených interaktivních cvičení je k dispozici také pracovní list k vytištění a rýsování na papíře:
NahoruKonstrukce trojúhelníků: těžnice, výšky, vepsaná a opsaná kružnice
Při řešení složitějších příkladů použijeme další pojmy související s trojúhelníkem, například výška, těžnice, střední příčka, kružnice opsaná či vepsaná.
Těžnice je úsečka, která spojuje vrchol trojúhelníku se středem protější strany. Každý trojúhelník má tři těžnice a jejich průsečík tvoří těžiště trojúhelníku. Těžiště rozděluje každou těžnici v poměru 2 : 1. Delší část těžnice je úsečka mezi vrcholem a těžištěm.
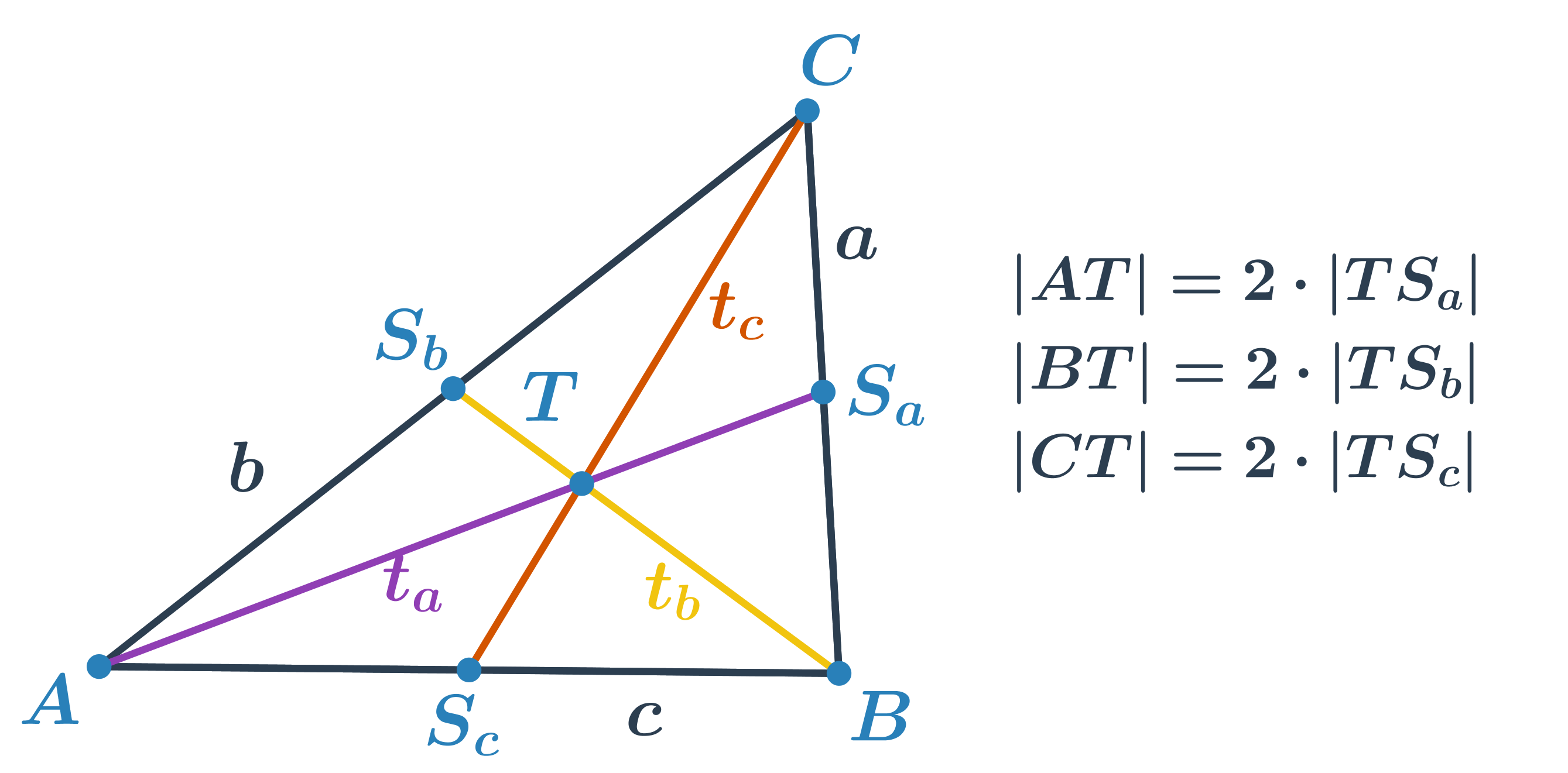
Střední příčka trojúhelníku je úsečka, která spojuje středy dvou stran v trojúhelníku. Je rovnoběžná se stranou, jejíž střed nespojuje a její délka je rovna polovině délky této strany.
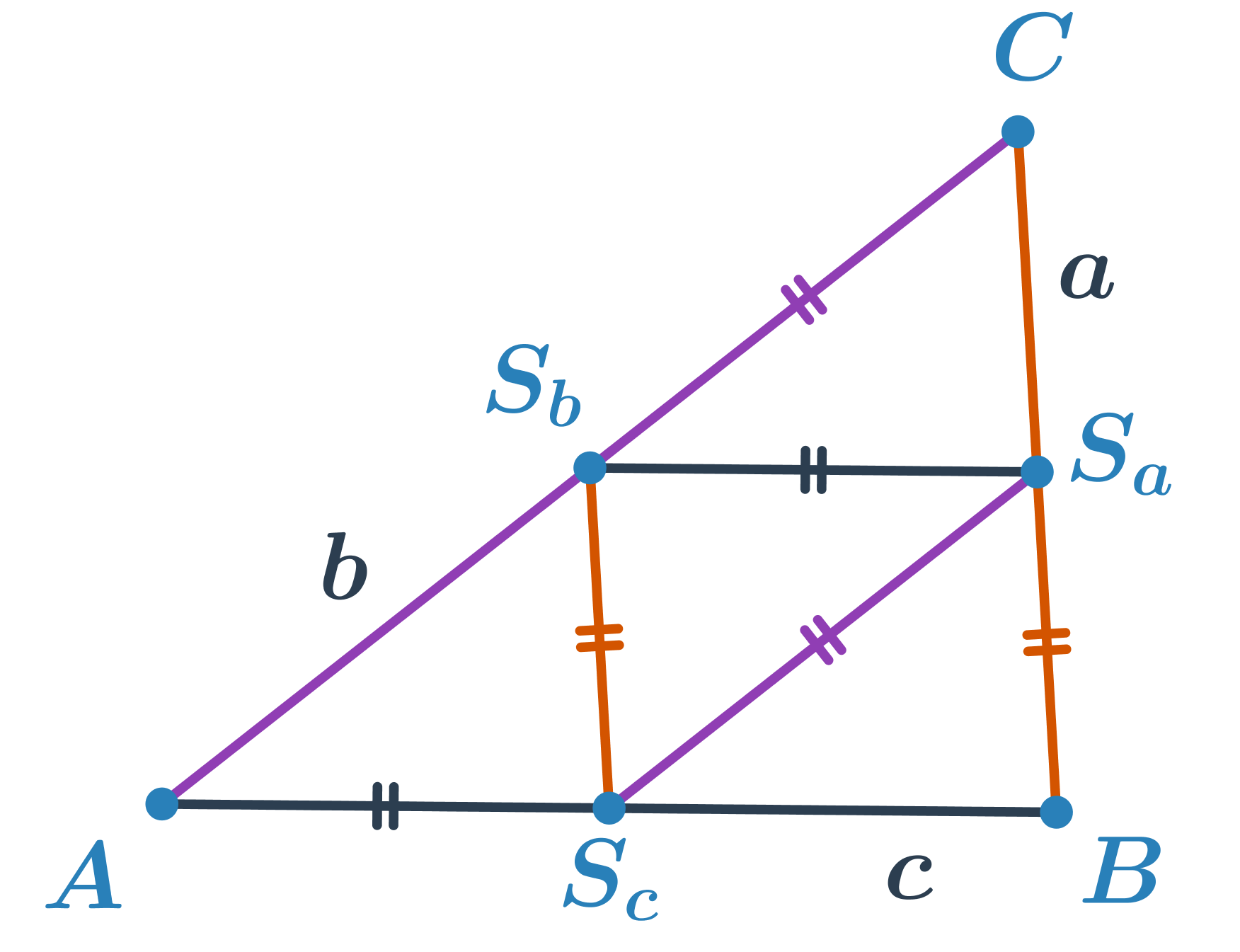
Kružnice opsaná je kružnice, která prochází všemi vrcholy trojúhelníka. Její střed leží v průsečíku os stran. To znamená, že střed kružnice opsané je stejně vzdálen od všech vrcholů trojúhelníku.
Kružnice vepsaná je kružnice, která se dotýká všech stran trojúhelníku. Její střed leží v průsečíku os vnitřních úhlů trojúhelníku. To znamená, že střed kružnice vepsané je stejně vzdálen od všech tří přímek, na kterých leží strany trojúhelníku.
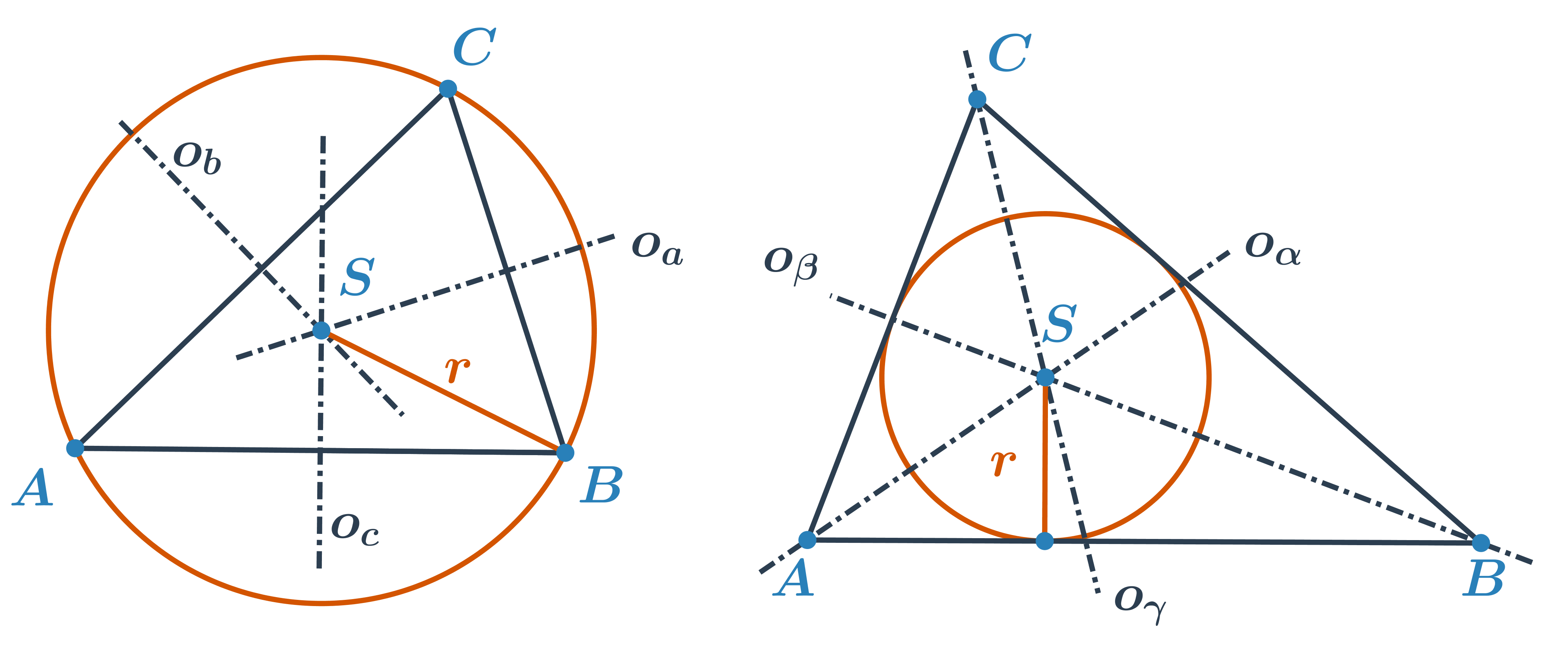
Kromě níže uvedených interaktivních cvičení jsou k dispozici také pracovní listy k vytištění a rýsování na papíře:
NahoruKonstrukční úlohy: čtyřúhelníky
Téma je rozděleno podle typů konstruovaných čtyřúhelníků:
- Konstrukce čtverců a obdélníků – základní konstrukce čtyřúhelníků, které mají všechny vnitřní úhly pravé
- Konstrukce rovnoběžníků – konstrukce čtyřúhelníků se dvěma dvojicemi rovnoběžných protějších stran
- Konstrukce lichoběžníků – konstrukce čtyřúhelníků s jednou dvojicí rovnoběžných protějších stran
- Konstrukce obecných čtyřúhelníků – konstrukce čtyřúhelníků, o kterých víme jen to, co si přečteme v zadání příkladu, nemusí splňovat žádné další podmínky
Kromě interaktivních cvičení jsou u jednotlivých témat k dispozici také pracovní listy k vytištění a rýsování na papíře:
Všechny pracovní listy na konstrukce čtyřúhelníků
Konstrukce čtyřúhelníků: čtverce a obdélníky
Konstrukce obdélníků
Při řešení konstrukčních úloh s obdélníky využíváme jejich následující vlastnosti:
- Všechny vnitřní úhly obdélníku jsou pravé, sousední strany jsou tedy na sebe kolmé.
- Protější strany jsou rovnoběžné.
- Všechny strany nemusí být stejně dlouhé. Stejně dlouhé jsou vždy dvě protější strany.
- Úhlopříčky obdélníku jsou stejně dlouhé a navzájem se půlí.
- Každému obdélníku lze opsat kružnici. Nazýváme ji kružnice opsaná, prochází vrcholy obdélníku a má střed v průsečíku úhlopříček.
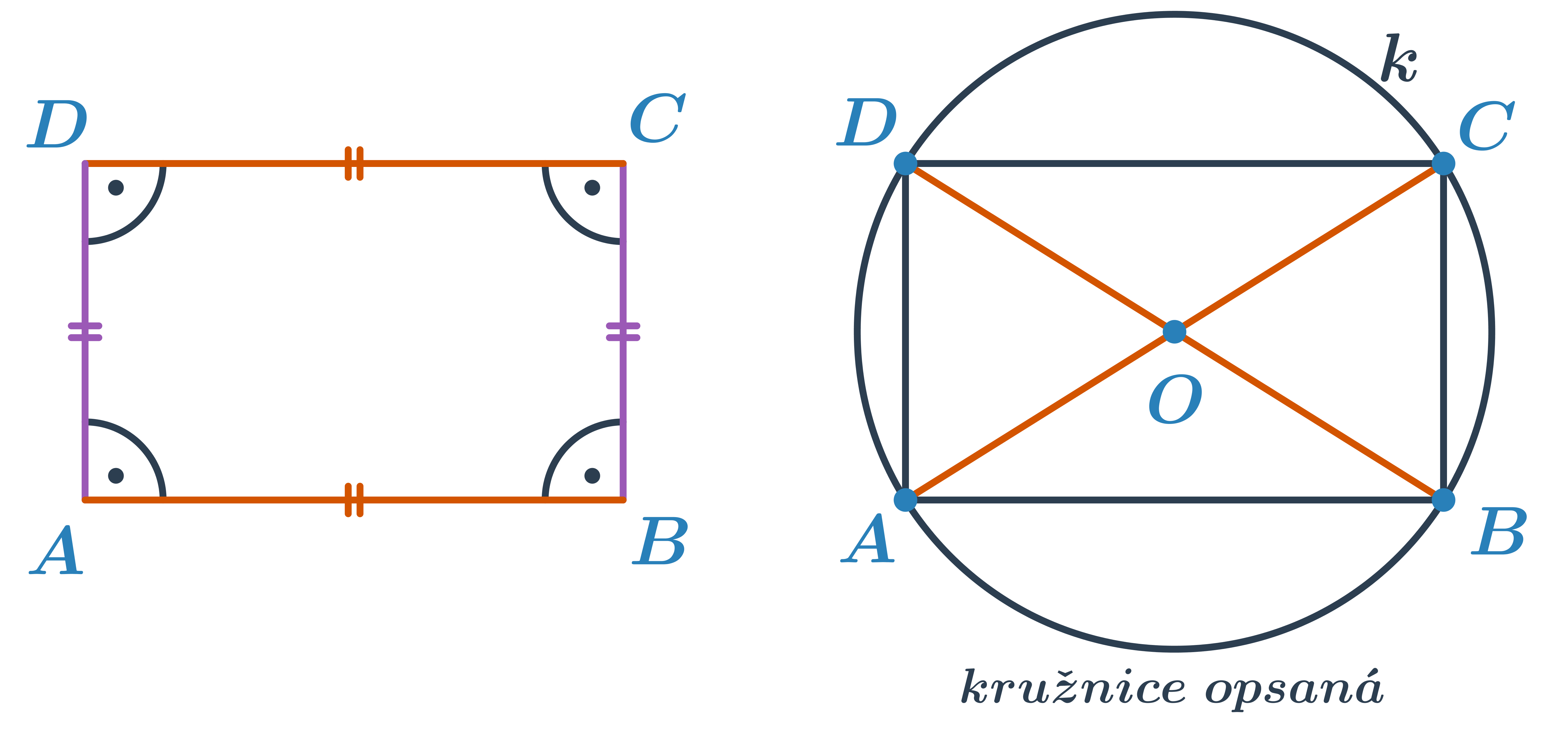
Konstrukce čtverců
Čtverec můžeme považovat za zvláštní případ obdélníku (nebo rovnostranného rovnoběžníku). Stejně jako obdélník má všechny vnitřní úhly pravé, sousední strany jsou na sebe kolmé a protější strany čtverce jsou rovnoběžné. Úhlopříčky čtverce se protínají v bodě, který nazýváme střed čtverce. Čtverce mají všechny pěkné vlastnosti obdélníků a ještě některé speciální navíc:
- Všechny strany čtverce jsou stejně dlouhé.
- Úhlopříčky čtverce jsou stejně dlouhé, jsou na sebe kolmé, procházejí středem čtverce a navzájem se půlí.
- Každému čtverci lze opsat kružnici. Nazýváme ji kružnice opsaná, prochází vrcholy čtverce a má střed ve středu čtverce.
- Každému čtverci lze také vepsat kružnici. Nazýváme ji kružnice vepsaná, dotýká se stran čtverce a má střed ve středu čtverce.
Kromě interaktivního procvičování níže jsou k dispozici ještě pracovní listy k vytištění a rýsování na papíře:
NahoruKonstrukce čtyřúhelníků: rovnoběžníky
Konstrukce rovnoběžníků
Rovnoběžník je speciální případ čtyřúhelníku, jehož protilehlé strany jsou rovnoběžné. Při řešení konstrukčních úloh využíváme následují vlastnosti rovnoběžníků:
- Protější strany jsou rovnoběžné.
- Všechny strany nemusí být stejně dlouhé. Stejně dlouhé jsou vždy dvě protější strany.
- Úhlopříčky rovnoběžníku nejsou stejně dlouhé, ale navzájem se půlí a protínají se ve středu rovnoběžníku.
- Každé dva protější úhly jsou stejné.
- Součet vnitřních úhlů u jedné strany je 180°.
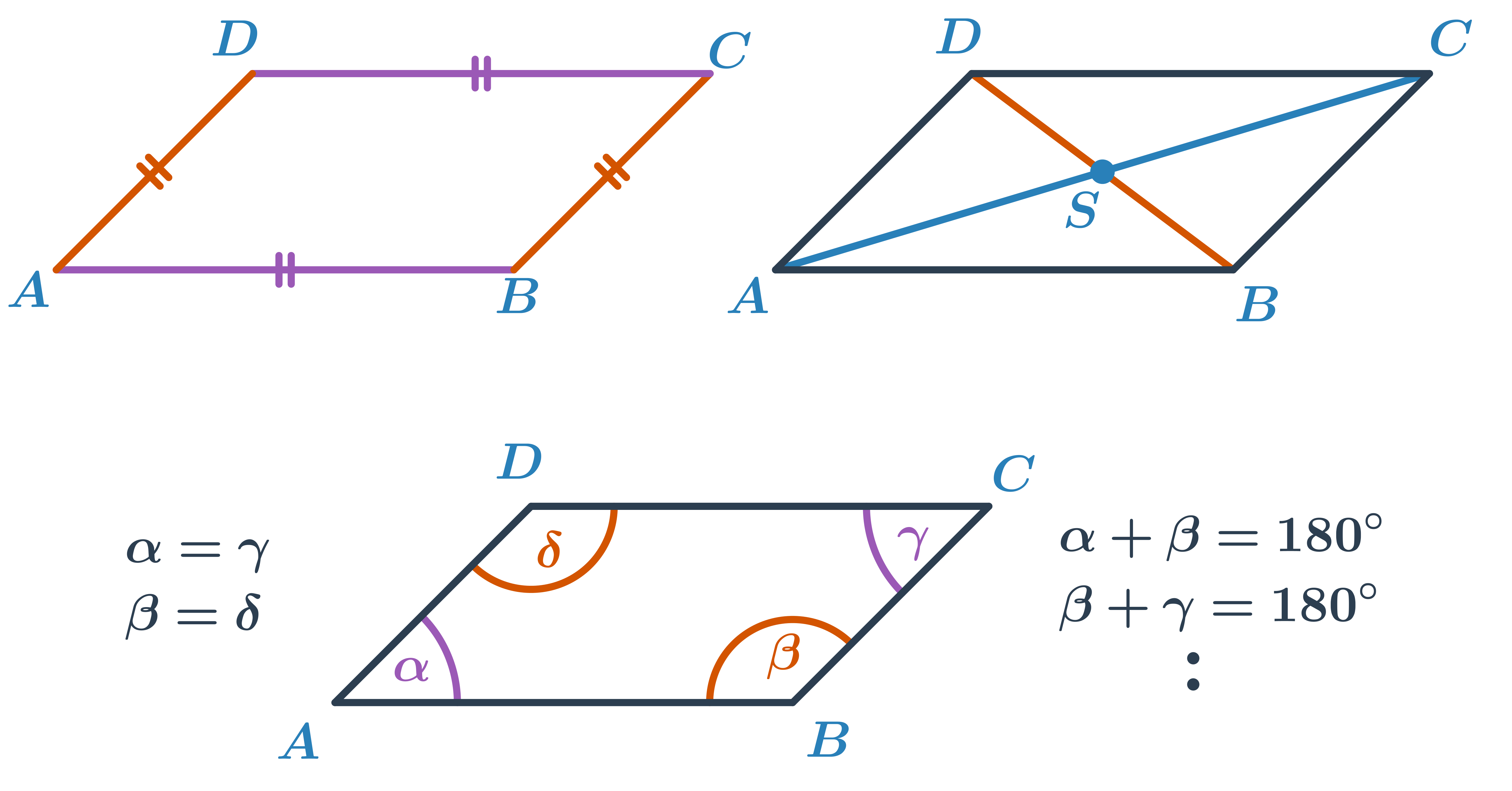
Při konstrukci rovnoběžníku potřebujeme znát tři údaje, ze kterých jsem často schopni sestrojit některý trojúhelník určený podle vět s vrcholy ve trojici vrcholů rovnoběžníku. Zbývající vrchol rovnoběžníku pak najdeme pomocí rovnoběžek nebo shodnosti protějších stran.
Příklad: Sestrojte rovnoběžník ABCD, je-li dáno a=8 cm, b=5 cm, \beta=110^\circ.
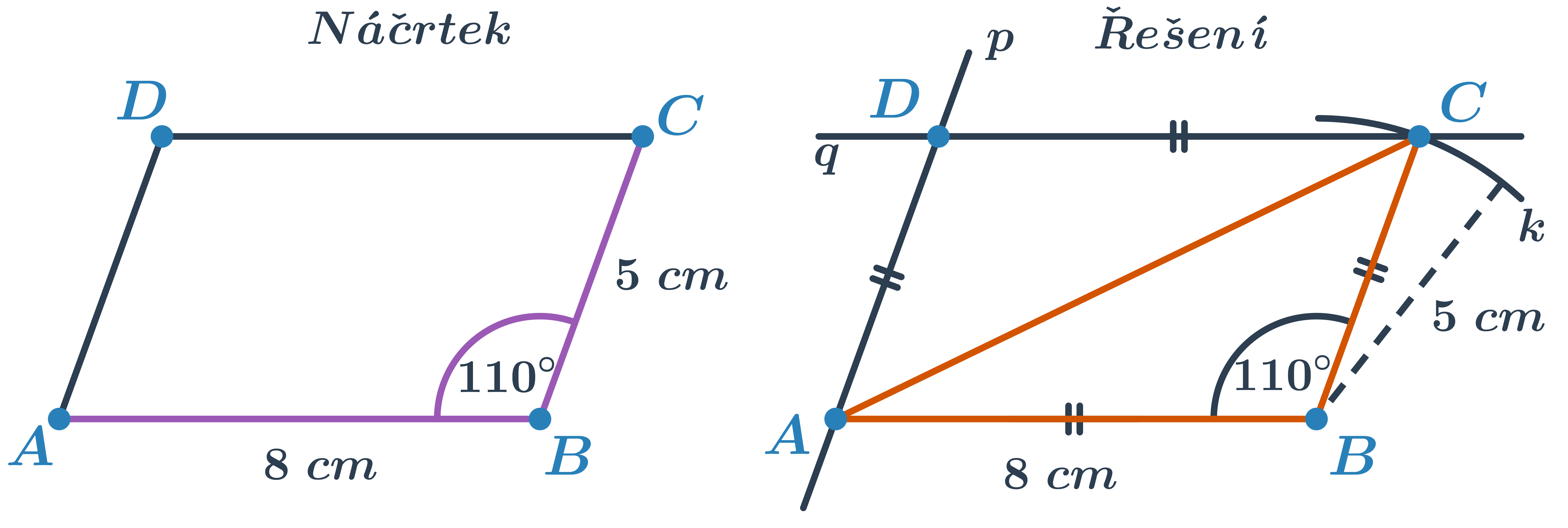
- Nejprve sestrojíme trojúhelník ABC určený podle věty sus.
- Pro konstrukci bodu D sestrojíme postupně ve vrcholech A a C rovnoběžky se stranami BC a AB.
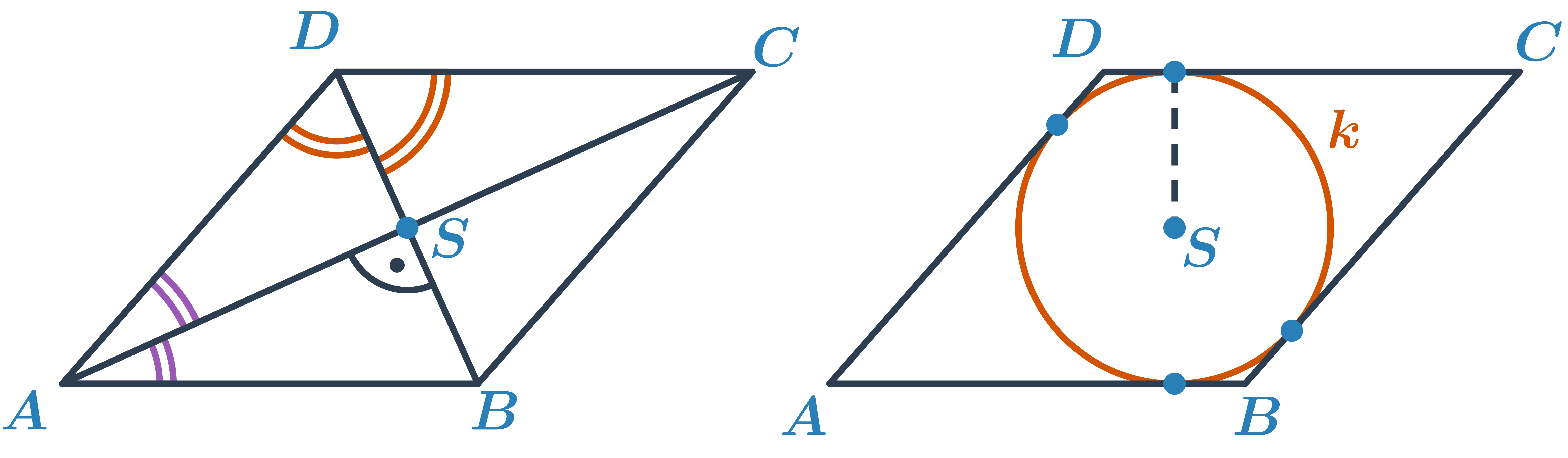
Konstrukce kosočtverců
Kosočtverec je speciální případ rovnoběžníku. Má všechny strany stejně dlouhé. Proti obecnému rovnoběžníku mají jeho úhlopříčky navíc dvě speciální vlastnosti – jsou na sebe kolmé a půlí vnitřní úhly. Kosočtverci lze (stejně jako čtverci) vepsat kružnici.
Kromě interaktivního procvičování níže je k dispozici ještě pracovní list k vytištění a rýsování na papíře:
NahoruKonstrukce čtyřúhelníků: lichoběžníky
Konstrukce lichoběžníků
Lichoběžník je čtyřúhelník, který má dvě rovnoběžné strany – ty se nazývají základny a dvě různoběžné strany – ramena. Vzdálenost základen se nazývá výška. Při konstrukcích budeme využívat následující vlastnosti:
- Základny jsou rovnoběžné.
- Úsečka spojující středy ramen se nazývá střední příčka a je rovnoběžná se základnami.
- Součet vnitřních úhlů u každého ramene je 180°.

Při konstrukci lichoběžníku potřebujeme znát čtyři údaje, ze kterých často dokážeme sestrojit trojúhelník určený podle vět s vrcholy ve třech vrcholech lichoběžníku. Zbývající vrchol lichoběžníku pak najdeme pomocí posledního údaje a rovnoběžnosti základen.
Příklad: konstrukce lichoběžníku, známé délky tří stran a úhlopříčky
Sestrojte lichoběžník ABCD, je-li dáno a=8 cm, b=6 cm, c=5 cm, |AC|=8 cm.
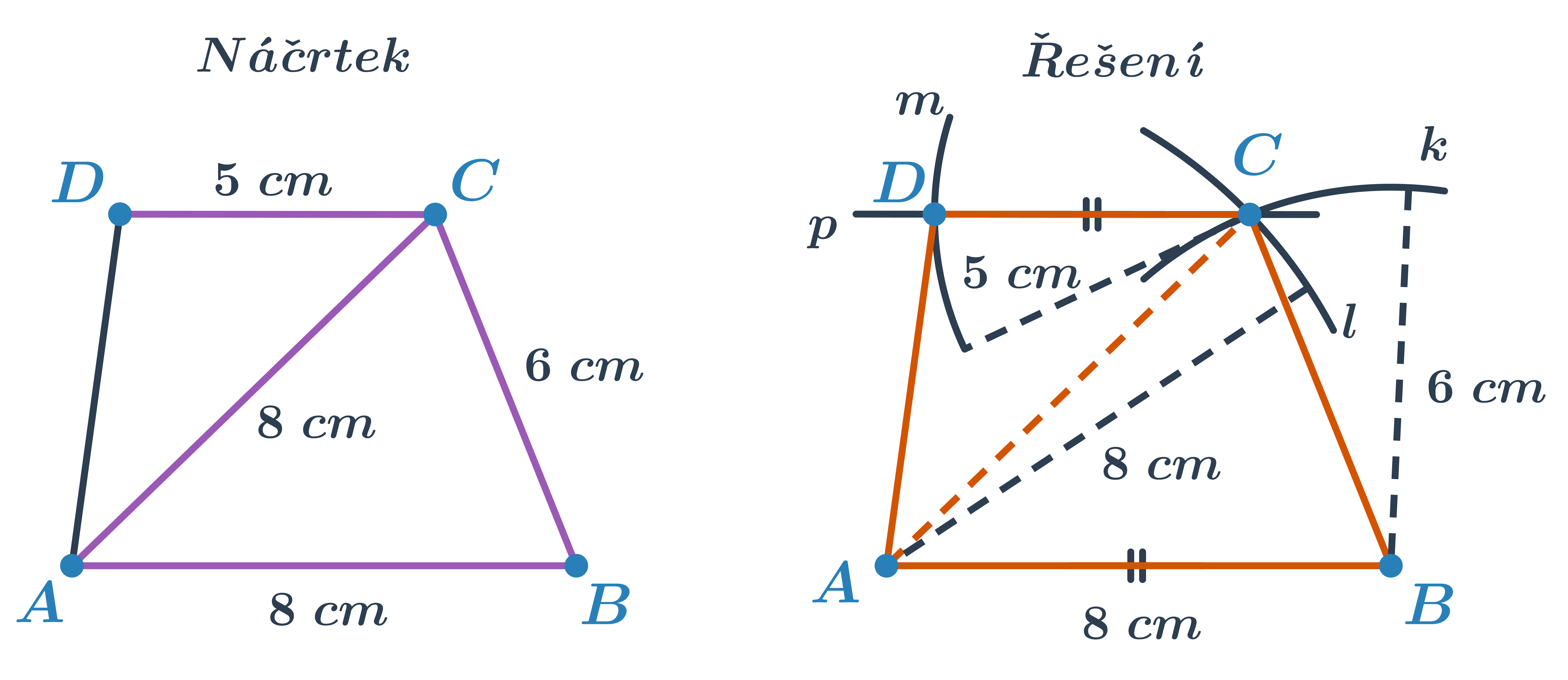
- Nejprve sestrojíme trojúhelník ABC určený podle věty sss.
- Základna CD je rovnoběžná se základnou AB. Bodem C tedy sestrojíme rovnoběžku p se stranou AB.
- Na tuto rovnoběžku pak naneseme délku strany c – poslední známý údaj.
Konstrukce rovnoramenných lichoběžníků
V rovnoramenném lichoběžníku mají obě ramena stejnou délku. Odpovídající vnitřní úhly u těchto ramen jsou pak stejné (dva stejné úhly \alpha = \beta u jedné základny a dva stejné úhly \gamma=\delta=180^\circ - \alpha u druhé základny). Úhlopříčky rovnoramenného lichoběžníku jsou stejně dlouhé. Narozdíl od obecného lichoběžníku mu lze opsat kružnici. Střed této opsané kružnice ale neleží v průsečíku úhlopříček.
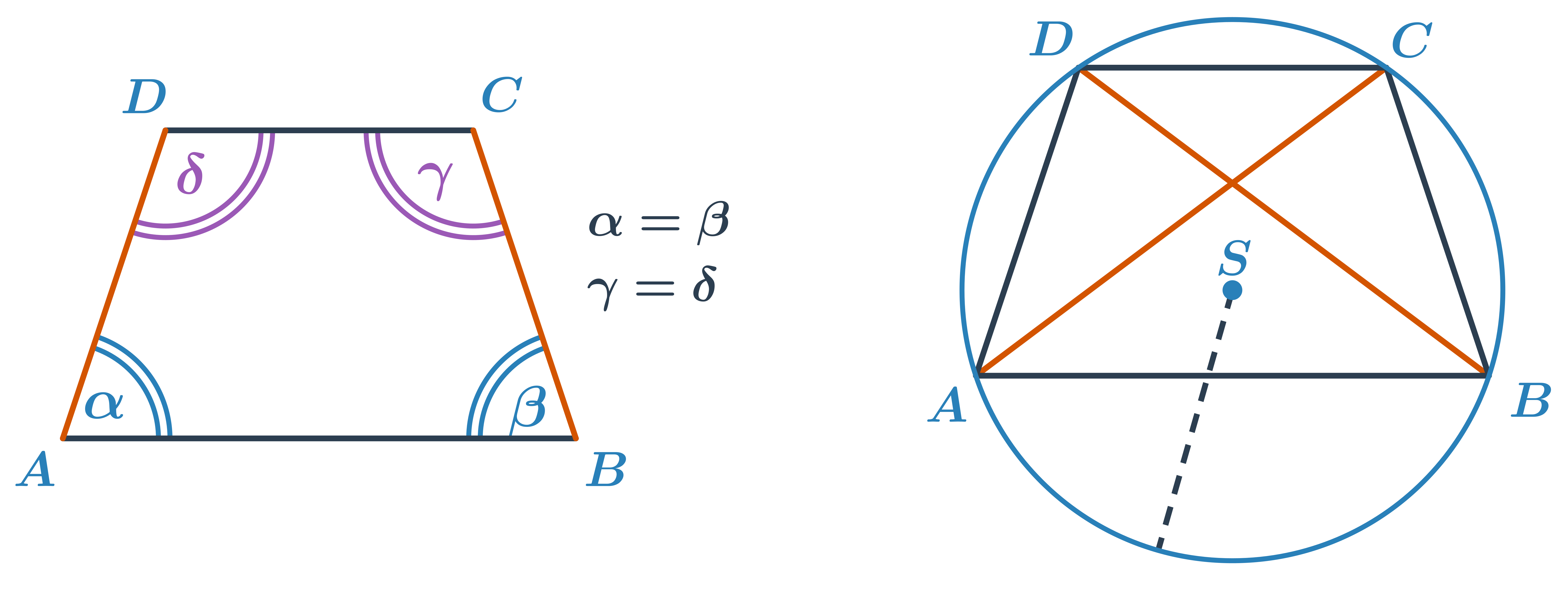
Kromě interaktivního procvičování níže je k dispozici ještě pracovní list k vytištění a rýsování na papíře:
NahoruKonstrukce obecných čtyřúhelníků
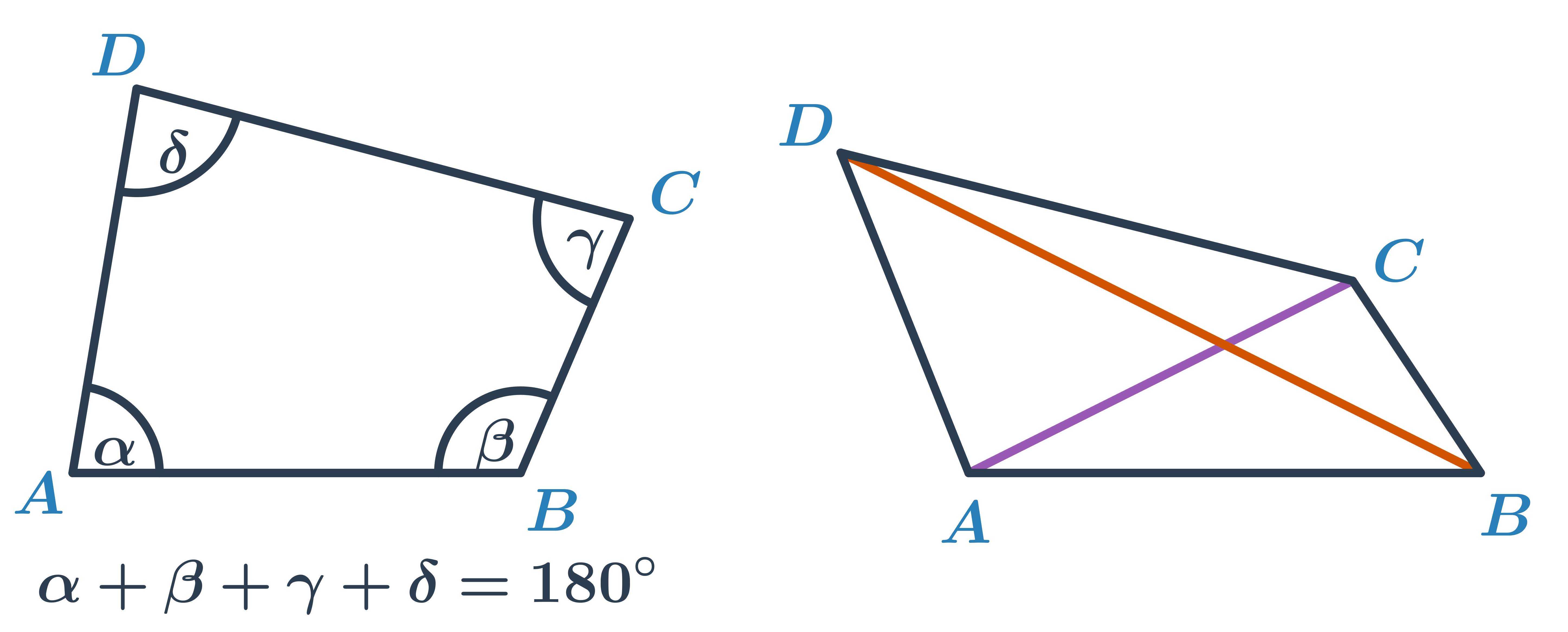
Víme, že čtyřúhelník je rovinný útvar ohraničený čtyřmi úsečkami, které spojují jeho vrcholy. Ve čtyřúhelníku může obecně být každá strana jinak dlouhá a každý vnitřní úhel může mít jinou velikost. Součet velikostí vnitřních úhlů je vždy 360^\circ. Pokud má čtyřúhelník všechny vnitřní úhly menší než 180^\circ, nazýváme ho konvexní. Speciálními případy konvexního čtyřúhelníku jsou čtverec, obdélník, rovnoběžník a lichoběžník. Pokud má čtyřúhelník jeden vnitřní úhel větší než 180^\circ, nazýváme ho nekonvexní.
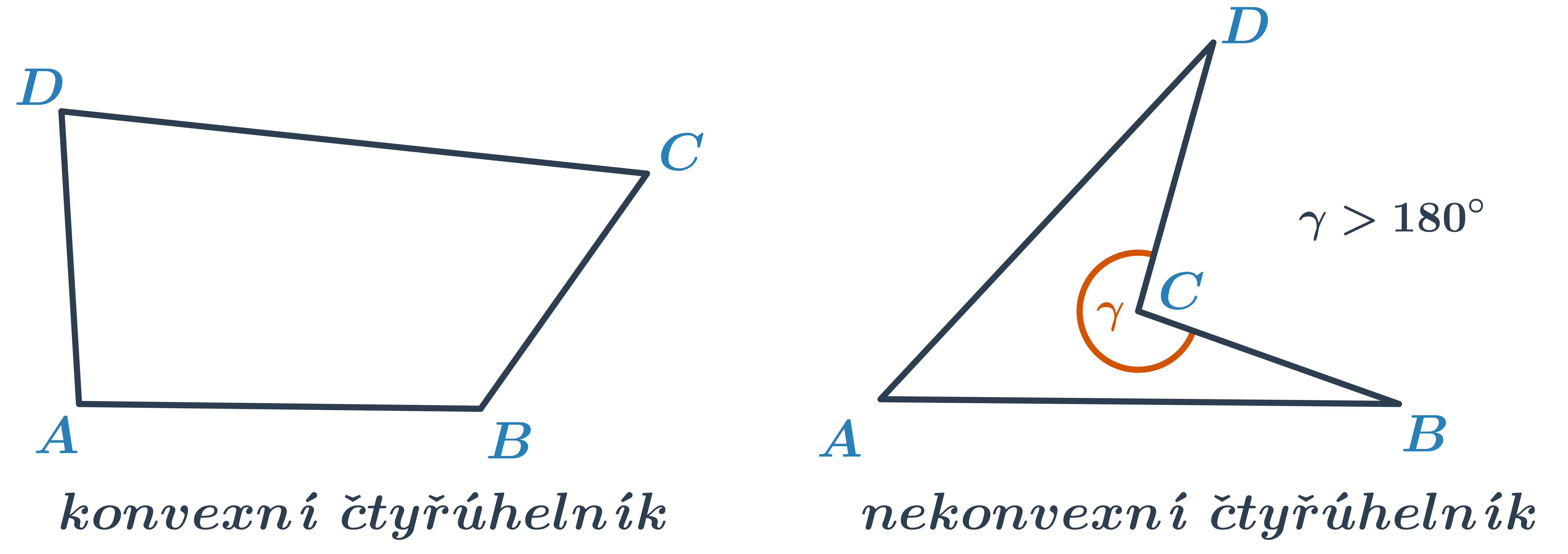
Úhlopříčky ve čtyřúhelníku mohou mít různou délku a rozdělují čtyřúhelník na dva trojúhelníky. Čtyřúhelník jako rovinný útvar si tak můžeme představit jako sjednocení dvou trojúhelníků. Toho často využijeme při konstrukci čtyřúhelníku, kdy jeden trojúhelník určený podle vět dokážeme sestrojit. Poslední vrchol pak doplníme pomocí zbývajících podmínek.
Příklad: konstrukce čtyřúhelníku, známé velikosti 3 stran a 2 úhlů
Sestrojte čtyřúhelník KLMN, je-li dáno |KL|=5 cm, |LM|=4 cm, |KN|=6 cm, |\sphericalangle NKL|=120^\circ,\ |\sphericalangle KLM|=100^\circ.
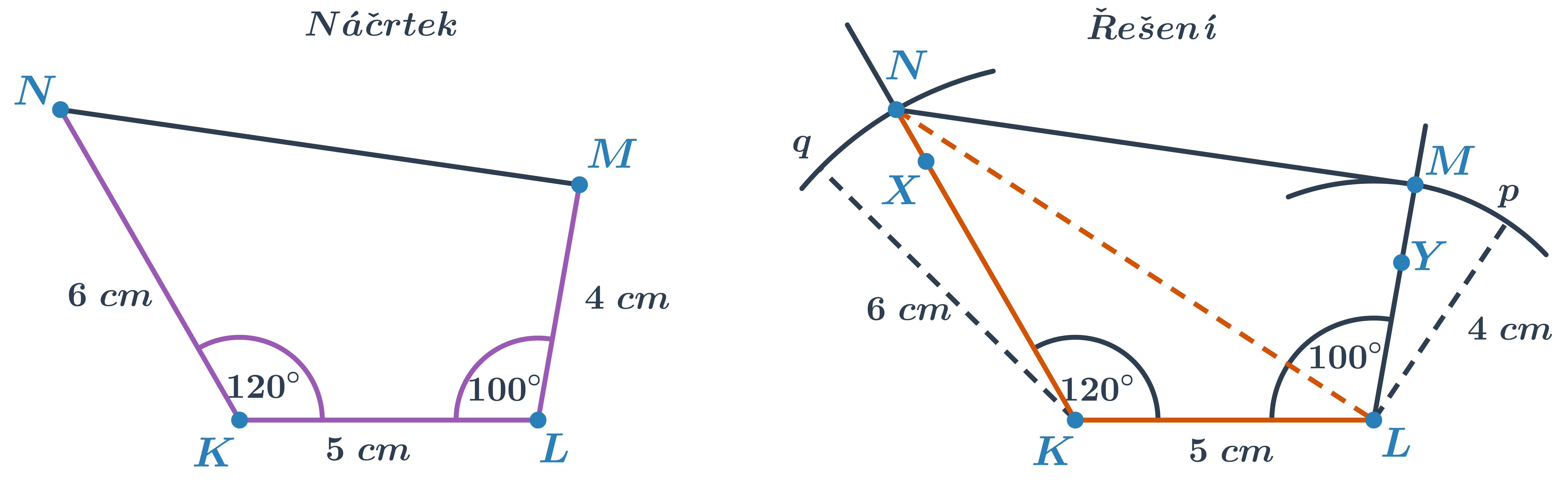
- Nejprve sestrojíme trojúhelník KLN určený podle věty sus.
- Dále sestrojíme úhel KLM pomocí polopřímky LY, která svírá s úsečkou KL úhel 100^\circ.
- Na polopřímku LY naneseme délku strany LM a dostaneme poslední vrchol M.
Kromě interaktivního procvičování níže je k dispozici ještě pracovní list k vytištění a rýsování na papíře:
NahoruKonstrukční úlohy průřezově
Při řešení složitějších konstrukčních úloh budeme využívat i množiny bodů daných vlastností. Připomeňme si ty nejdůležitější.
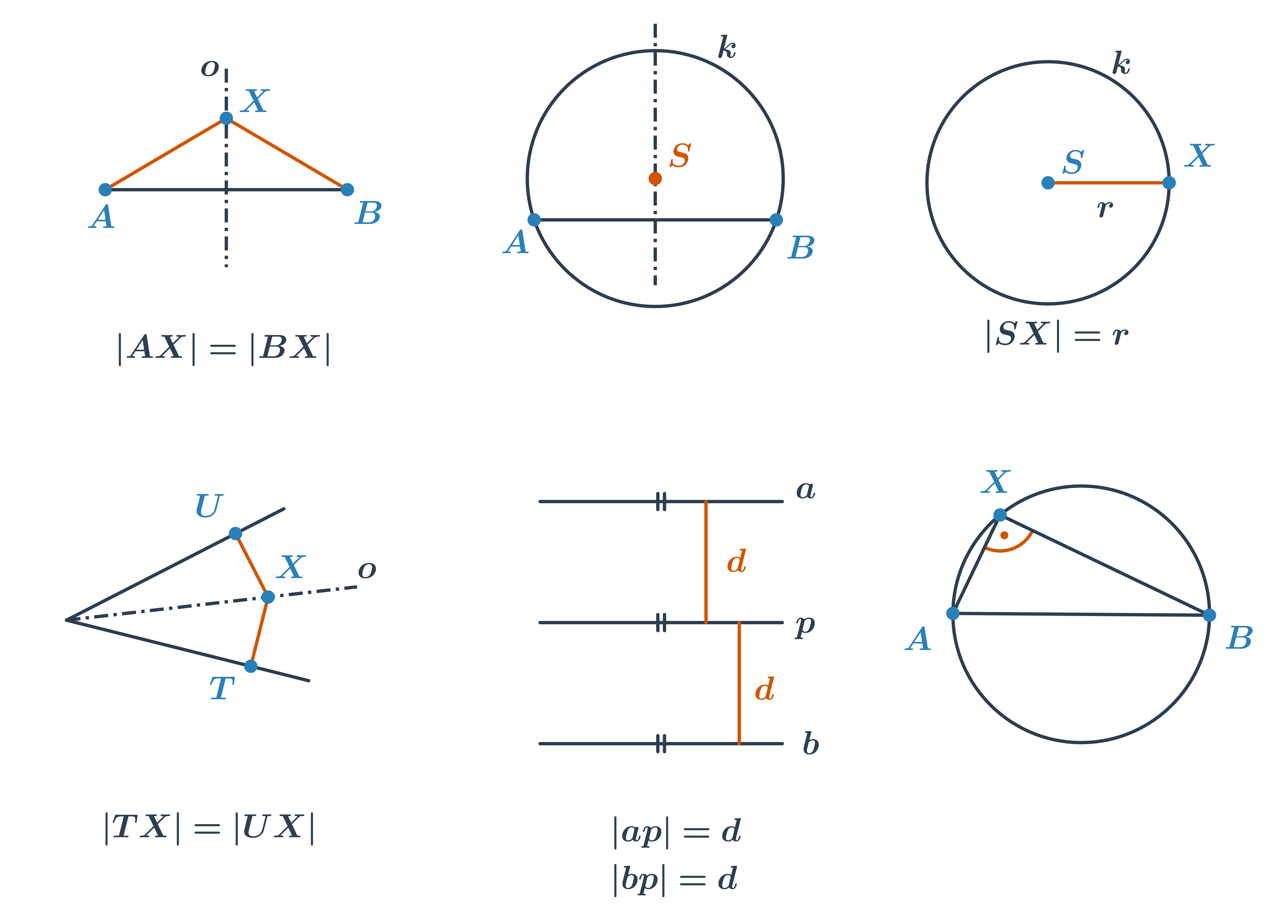
| osa úsečky AB | množina všech bodů, které mají od bodů A, B stejnou vzdálenost |
| osa úsečky AB | množina středů všech kružnic, které prochází body A, B |
| kružnice | množina všech bodů, které mají od bodu S stejnou vzdálenost (poloměr r) |
| osa úhlu | množina všech bodů, které mají od ramen úhlu stejnou vzdálenost |
| rovnoběžky | množiny všech bodů, které mají od přímky p stejnou vzdálenost |
| Thaletova kružnice nad úsečkou AB | množina všech vrcholů pravých úhlů, jejichž ramena procházejí body A, B |
Kromě níže uvedených interaktivních cvičení je k dispozici také pracovní list k vytištění a rýsování na papíře:
Nahoru
