Mocniny a odmocniny

Umocňování je opakované násobení. Například 3^5 = 3\cdot 3\cdot 3\cdot 3\cdot 3 = 243. Odmocňování je opačnou operací k umocňování. Například druhá odmocnina z 36 je 6 (\sqrt{36}=6), protože 6^2 = 6\cdot 6 = 36. Mocniny a odmocniny využíváme v mnoha oblastech matematiky, například při práci s mnohočleny, řešení kvadratických rovnic, výpočtu obsahu a objemu nebo při určování délek stran v trojúhelníku.

Prvním krokem pro zvládnutí tohoto tématu jsou základní mocniny a odmocniny, kde pracujeme s malými, přirozenými čísly. Pro tato čísla se vyplatí se naučit základní mocniny a odmocniny zpaměti, protože na ně často v matematice narazíme.

Jako další krok potřebujeme zvládnout pracovat s výrazy s mocninami a odmocninami.

Umocňování je možné definovat i pro záporný mocnitel. Tento způsob umocňování se využívá pro vědecký zápis čísel, který nám umožňuje přehledně pracovat s velmi velkými či velmi malými čísly, díky čemuž má hojné využití ve fyzice.

Umocňování a odmocňování můžeme přirozeně používat i ve spojitosti se zlomky a desetinnými čísly.

Mocniny jsou zkráceným zápisem opakujícího se násobení. Příklady:

• 3^2 = 3\cdot 3 = 9
• 2^3 = 2\cdot 2 \cdot 2= 8
• 5^4 = 5\cdot 5\cdot 5\cdot 5 = 625

Při umocňování záporných čísel je výsledek kladný pro sudé mocniny, záporný pro liché mocniny.

• (-3)^2 = (-3)\cdot (-3) = 9
• (-3)^3 = (-3)\cdot (-3)\cdot (-3) = -27
• (-3)^4 = (-3)\cdot (-3)\cdot (-3)\cdot (-3) = 81

Nultá mocnina jakéhokoliv čísla je 1 (např. 5^0=1, 564^0=1). Nula umocněna na libovolné číslo je 0 (např. 0^3 = 0\cdot 0\cdot 0 = 0). Což vede na zajímavou otázku: Čemu se rovná 0^0?

Odmocňování v matematice je částečně inverzní (opačnou) operací k umocňování. Druhá odmocnina z čísla x je takové nezáporné číslo a, pro které platí a^2 = x. Druhou odmocninu značíme \sqrt{x}. Příklady:

• \sqrt{9} = 3, protože 3^2 = 9
• \sqrt{25} = 5, protože 5^2 = 25
• \sqrt{100} = 10, protože 10^2 = 100

Obecně pak n-tá odmocnina z x je takové číslo a, pro které platí a^n = x, n-tou odmocninu značíme \sqrt[n]{x}. Příklady:

• \sqrt[3]{125} = 5, protože 5^3 = 25
• \sqrt[5]{32} = 2, protože 2^5 = 32
• \sqrt[4]{10000} = 10, protože 10^4 = 10000

Odmocňování má i geometrický význam. Pokud máme čtverec o obsahu S, pak tento čtverec má délku strany rovnou druhé odmocnině \sqrt{S}. Pokud máme krychli o objemu V, pak tato krychle má délku hranu rovnou třetí odmocnině \sqrt[3]{V}. Odmocniny hojně využijeme například při aplikaci Pythagorovy věty.

Graf funkce odmocnina

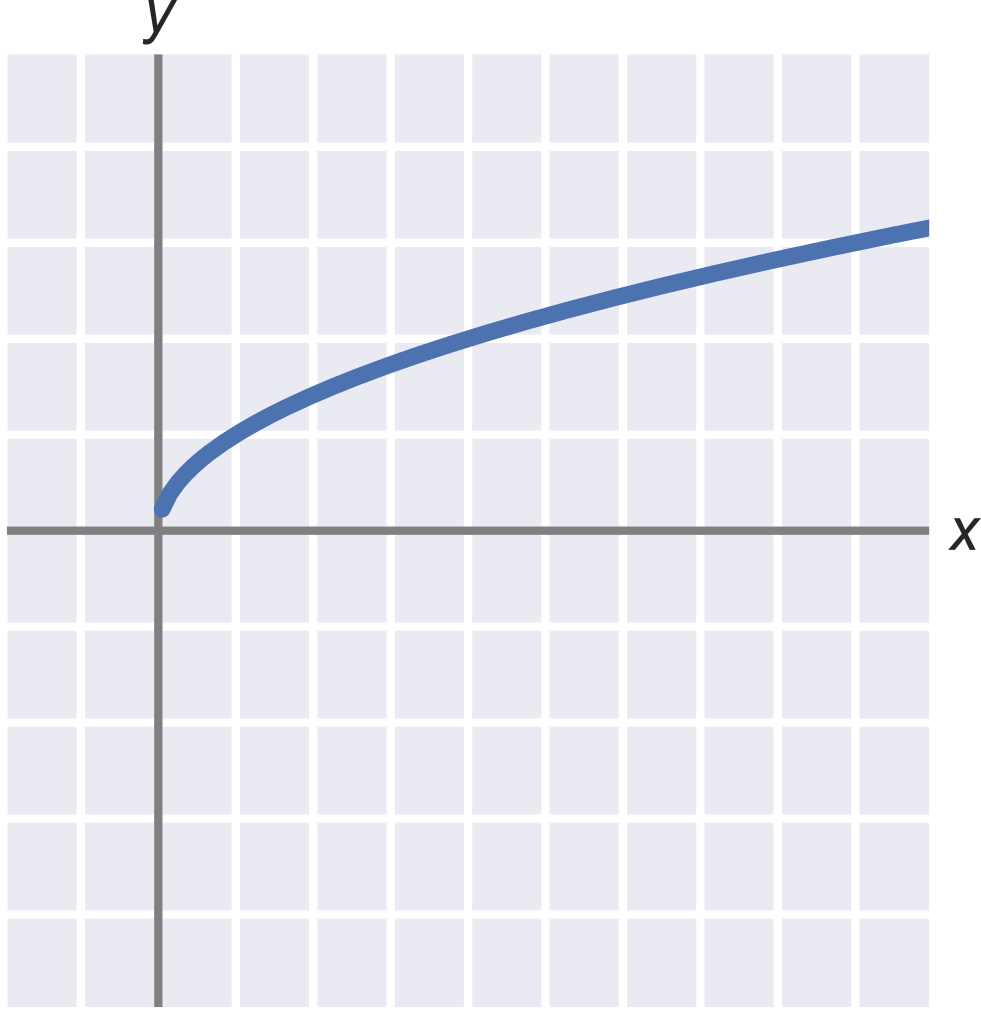
Odmocnina a záporná čísla

Když hledáme odmocninu třeba z 25, tak hledáme číslo, které po umocnění dá 25. To splňuje 5\cdot 5, ale také (-5)\cdot (-5). Odmocnina je však definována jako nezáporné číslo, takže \sqrt{25} = 5.

Druhou odmocninu můžeme počítat pouze z kladných čísel, protože jakékoliv číslo umocněné na druhou je kladné. Odmocnina ze záporných čísel není definována. Nebo vlastně je, ale to musíme zavést komplexní čísla (což je velice zajímavý a užitečný nástroj, ale trochu pokročilý a ten tu nebudeme rozebírat).

Pro běžná reálná čísla můžeme počítat odmocniny za záporných čísel pro liché stupně n. Například:

• \sqrt[3]{-8} = -2, protože (-2)^3 = -8
• \sqrt[5]{-100000} = -10, protože (-10)^5 = -100000

Pro mocniny platí následující vztahy:

• x^0 = 1
• x^a \cdot x^b = x^{a+b}
• x^a : x^b = x^{a-b}
• (x^a)^b = x^{a\cdot b}
• (x\cdot y)^a = x^a\cdot y^a

Konkrétní příklady, která názorně ilustrují, proč uvedené vztahy platí:

• 7^3\cdot 7^2 = (7\cdot 7\cdot7) \cdot (7\cdot 7) = 7^{3+2} = 7^5
• 6^4: 6^2 = (6\cdot 6\cdot 6\cdot 6) : (6\cdot 6) = 6^{4-2} = 6^2
• (5^3)^2 = (5\cdot 5\cdot 5)^2 = (5\cdot 5\cdot 5) \cdot (5\cdot 5\cdot 5) = 5^{3\cdot 2} = 5^6
• (7\cdot 8)^3 = (7\cdot 8) \cdot (7\cdot 8) \cdot (7\cdot 8) = (7\cdot 7\cdot 7) \cdot (8\cdot 8\cdot 8) = 7^3 \cdot 8^3

Pro odmocniny platí následující vztahy (předpokládáme x, y > 0):

• \sqrt{0} = 0
• \sqrt{1} = 1
• \sqrt{x}\cdot \sqrt{x} = x
• \sqrt{xy} = \sqrt{x} \cdot \sqrt{y}
• \sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}}
• \sqrt[n]{x^k} = x^{\frac{k}{n}}
• \sqrt[n]{\sqrt[m]{x}} = \sqrt[n\cdot m]{x}

Příklady:

• \sqrt{24} = \sqrt{4\cdot 6} = \sqrt{4} \cdot \sqrt{6} = 2\sqrt{6}
• \sqrt{3} \cdot \sqrt{3} = (\sqrt{3})^2 = 3
• \sqrt[3]{5^6} = 5^\frac63 = 5^2 = 25

Mocnina se záporným exponentem odpovídá převrácené hodnotě příslušné mocniny s kladným exponentem. Tedy vzorec. Toto pravidlo je důsledkem vlastnosti násobení vzorec. Musí tedy platit vzorec.

Konkrétní příklady:

• vzorec
• vzorec
• vzorec
• vzorec

Vědecký zápis čísel je zápis čísel pomocí součinu m\cdot 10^n, kde m je reálné číslo (mantisa) a 10^n je mocnina desítky. Tento zápis čísel je užitečný zejména při práci s velmi velkými nebo velmi malými čísly. Například hmotnost Země je přibližně 5970000000000000000000000 kg, což je daleko přehlednější v zápisu 5{,}97\cdot 10^{24} kg. Příklady:

Umocňování a odmocňování zlomku

Při umocňování (odmocňování) zlomku prostě umocníme (odmocníme) čitatele i jmenovatele:

• \large(\frac{2}{3}\large)^2 = \frac{2^2}{3^2} = \frac{4}{9}

• \sqrt{\frac{2}{3}} = \frac{\sqrt{2}}{\sqrt{3}}

• \large(\frac{4}{5}\large)^{-1} = \frac{4^{-1}}{5^{-1}} = \frac{5}{4} (umocňování na -1 odpovídá prohození čitatele a jmenovatele)

Umocňování na zlomek

Umocňování na zlomek odpovídá tomu, že vezmeme mocninu podle čitatele a odmocninu podle jmenovatele, tj. x^\frac{a}{b} = \sqrt[b]{x^a}. Příklady:

• 2^\frac{2}{3} = \sqrt[3]{2^2} = \sqrt[3]{4} = 1{,}587\ldots

• 4^\frac{1}{2} = \sqrt{4^1} = 2

• 81^\frac{3}{4} = \sqrt[4]{81^3} = \sqrt[4]{81}^3 = 3^3 = 27