Výpis souhrnů
Množiny
Podtémata
Množina je soubor prvků. Množiny využíváme jako dílčí prvek v mnoha oblastech matematiky. Příklad z geometrie: kružnice je množina bodů, které mají stejnou vzdálenost od středu. Množiny mají i mnoho praktických využití. Například při vývoji internetového obchodu program pracuje s množinou dostupných výrobků. Množiny jsou také důležité pro studium základů matematiky. Pomáhají nám například ujasnit si, co je to nekonečno.
K procvičování množin máme následující podtémata:
- Pojmy a značení – prázdná množina (\emptyset), průnik (A \cap B), podmnožina (A \subseteq B)…
- Zápis množin – zápis výčtem, zápis charakteristickou vlastností, standardní značky (\mathbb{N}, \mathbb{R})
- Množinové operace – průnik, sjednocení, rozdíl, symetrický rozdíl, aplikace na konkrétní příklady množin
- Vlastnosti množin a množinových operací – podmnožiny, množinové operace, jejich vzájemné vztahy, zápis obecných vlastností pomocí matematické notace
- Vennovy diagramy – grafické znázornění množin, jejich vztahů a operací s nimi
- Množiny množin, potenční množina – pokročilejší téma, kdy uvažujeme množiny, které mohou obsahovat jako svoje prvky jiné množiny
Množiny: pojmy a značení
Množina je soubor prvků. U množiny není důležité pořadí prvků a nezohledňuje opakované výskyty prvků. Následující množiny jsou tady všechny stejné:
- \{\square, \bigcirc, \triangle\}
- \{\bigcirc, \triangle, \square\}
- \{\square, \square, \square, \bigcirc, \bigcirc, \triangle\}
| Značení | Pojem | Komentář |
|---|---|---|
| \emptyset | prázdná množina | |
| \overline{A} | doplněk | prvky, které nepatří do množiny A |
| x \in A | patří do množiny | prvky x patří do množiny A |
| A \cap B | průnik | prvky, které patří do obou množin A, B |
| A \cup B | sjednocení | prvky, které patří alespoň do jedné z množin A, B |
| A \setminus B | rozdíl | prvky, které patří do množiny A, ale nepatří do B |
| A = B | rovnost | rovnost množin A, B |
| A \subseteq B | podmnožina | všechny prvky množiny A patří i do množiny B |
| A \subset B | vlastní podmnožina | A je podmnožina B a současně A \neq B |
| |A| | velikost množiny | počet prvků množiny |
| A \cap B = \emptyset | disjunktní množiny | množiny A, B nemají žádný společný prvek |
Zápis množin
Důležité číselné množiny mají v matematice svoje standardní označení:
| \mathbb{N} | množina přirozených čísel |
| \mathbb{Z} | množina celých čísel |
| \mathbb{Q} | množina racionálních čísel |
| \mathbb{R} | množina reálných čísel |
Ostatní množiny zapisujeme dvěma hlavními způsoby:
Zápis výčtem. Prostě vyjmenujeme prvky množiny a zapíšeme je pomocí složené závorky. Například M = \{3, 7, 9\} je tříprvková množina obsahující čísla 3, 7 a 9.
Zápis pomocí charakteristické vlastnosti. Určíme, ze které množiny prvky vybíráme a jakou musí splňovat vlastnost. Například M = \{x \in \mathbb{N} \mid x \lt 10\} je množina přirozených čísel menších než 10.
NahoruMnožinové operace
| Značení | Pojem | Komentář |
|---|---|---|
| A \cap B | průnik | prvky, které patří do obou množin A, B |
| A \cup B | sjednocení | prvky, které patří alespoň do jedné z množin A, B |
| A \setminus B | rozdíl | prvky, které patří do množiny A, ale nepatří do B |
| A \ominus B | symetrický rozdíl | prvky, které patří právě do jedné z množinA a B |
Znázornění množinových operací pomocí Vennových diagramů:
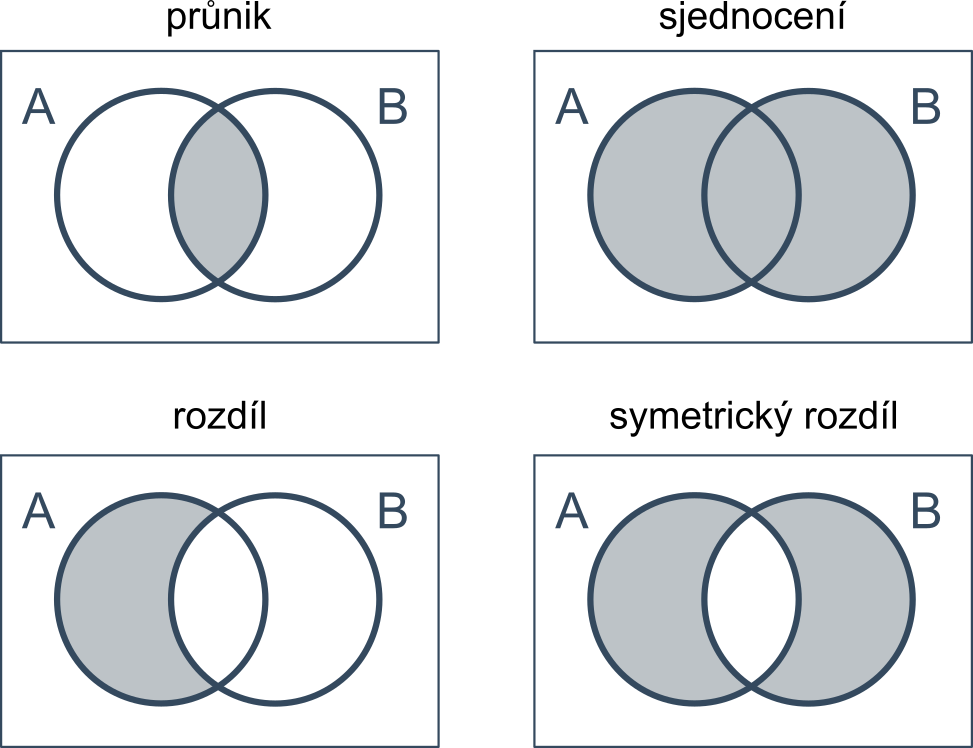
Vlastnosti množin a množinových operací
- Každá množina je svou podmnožinou: A\subseteq A
Příklady A\subseteq B
Příklady množin A, B splňující A \subseteq B:
- A = \{11, 50, 415\}, B = \{11, 50, 333, 415\}
- A = \{1,4,8\}, B = \{1,4,8\}
- A = množina všech přirozených čísel, B = množina všech celých čísel
- Množina nemůže být svou vlastní podmnožinou: A\not\subset A
Příklady A\subset B a A \not\subset B
Příklady množin A, B splňující A \subset B:
- A = \{11, 50, 415\}, B = \{11, 50, 333, 415\} (kvůli přítomnosti čísla 333 v množině B)
- A = množina všech přirozených čísel, B = množina všech celých čísel (záporná čísla jsou v množině všech celých čísel, ale nejsou v množině všech přirozených čísel)
Příklady množin, pro které A \not\subset B:
- A = \{1, 4, 8\}, B = \{1,4,8\} (protože v B není žádný prvek, který by nebyl v A)
- Prázdná množina je podmnožina jakékoliv množiny: \emptyset \subseteq A
- Prázdná množina nemá žádnou vlastní podmnožinu.
- A \subseteq A \cup B
- A \cap B \subseteq A
- A \subseteq B \wedge B \subseteq A \Leftrightarrow A=B
Vennovy diagramy
Vennův diagram znázorňuje všechny možné vztahy několika množin. Vennův diagram znázorňuje prvky množin jako body v rovině a množiny jako plochy uvnitř křivek. Nejčastěji používané jsou Vennovy diagramy pro dvě a tři množiny, ve kterých jsou množiny znázorněny pomocí kruhů. Je možné ztvárnit Vennovy diagramy i pro více množin, ale k tomu již nevystačíme s kruhy (tyto diagramy nejsou přehledné a tudíž se příliš nevyužívají).
Typický Vennův diagram pro tři množiny:
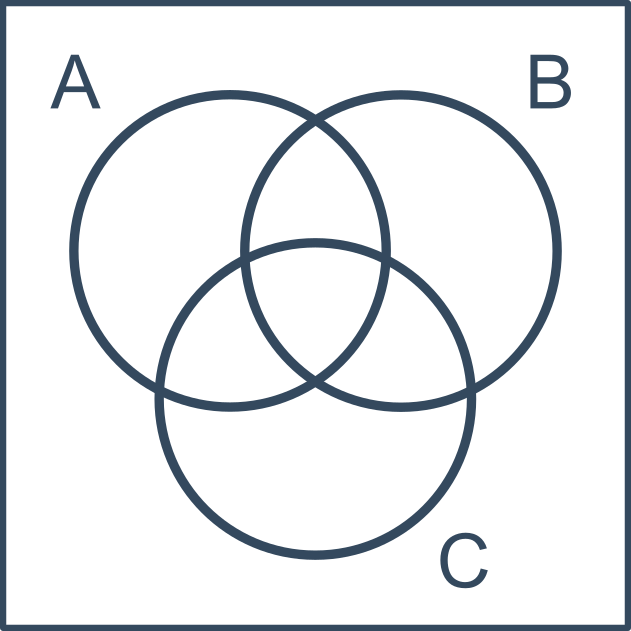
Příklad s konkrétními prvky (množina A obsahuje červené útvary, množina B obsahuje kolečka, množina C obsahuje vyplněné útvary):
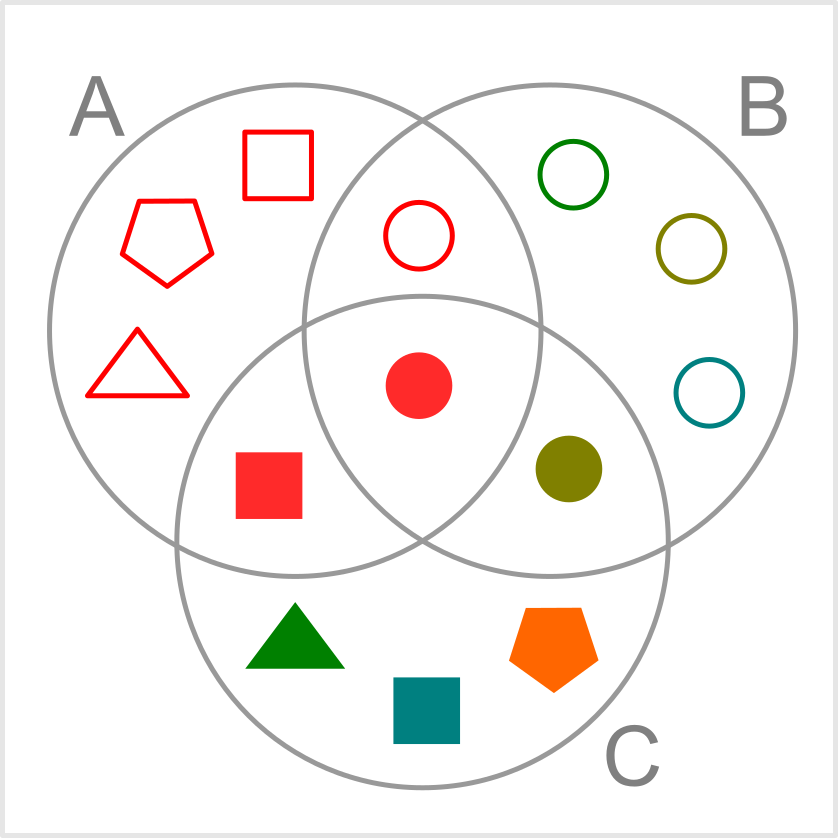
Vennovy diagramy využíváme například pro názornou ilustraci množinových operací. Následující obrázek ilustruje B \cap (A \cup C):
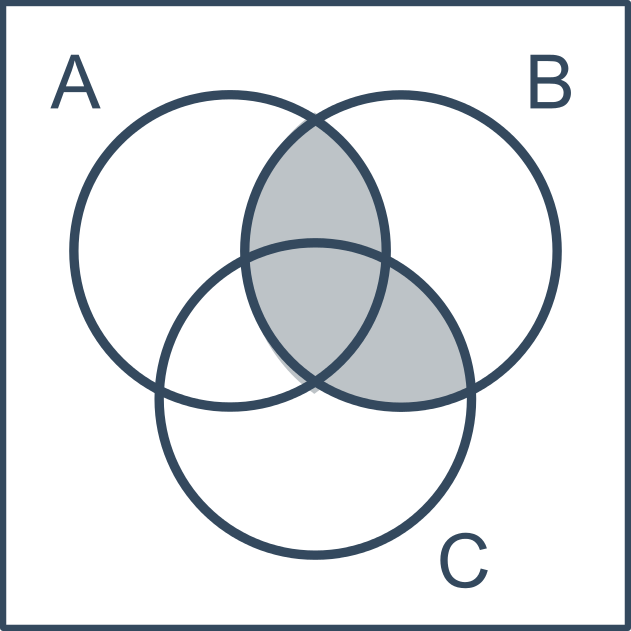
Pracovní list
Kromě interaktivního procvičování je k dispozici také pracovní list pro tisk:
Komiks pro zpestření
Množiny množin, potenční množina
Množina prvkem množiny
Prvkem množiny může být i jiná množina. S takovým prvkem pracujeme stejně jako s jinými prvky, jen se nesmíme nechat zmást.
Příklad: Množina M = \{a, \{b, c, d, e\}, \emptyset\} obsahuje tři prvky:
- „obyčejný“ prvek a
- čtyřprvkovou množinu \{b, c, d, e\}
- prázdnou množinu \emptyset
Pozor na rozdíl mezi prázdnou množinou a množinou obsahující prázdnou množinu:
- \emptyset (též můžeme psát \{\}) je prázdná množina, její velikost je 0,
- \{\emptyset\} je množina obsahující prázdnou množinu, její velikost je 1.
Potenční množina
Potenční množina množiny M obsahuje všechny podmnožiny množiny M. Potenční množinu značíme \mathcal{P}(M) (existují i další značení, například 2^M).
Příklad: Pro množinu M = \{a, b, c\} jsou všechny její podmnožiny:
- \{\}
- \{a\}
- \{b\}
- \{c\}
- \{a, b\}
- \{a, c\}
- \{b, c\}
- \{a, b, c\}
Potenční množina je množina všech těchto množin, tj. \mathcal{P}(M)=\{\{\}, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\}\}.
Potenční množina množiny M vždy obsahuje jako svůj prvek samotnou množinu M. Každá potenční množina také obsahuje jako svůj prvek prázdnou množinu.
Nahoru
