Výpis souhrnů
Úhly
Podtémata
Úhel je část roviny vymezená dvěma polopřímkami. Velikost úhlu měříme nejčastěji ve stupních, přičemž plný úhel má velikost 360°. Úhly využíváme v mnoha oblastech geometrie a mají bohaté praktické využití ve fyzice, navigaci (azimuty) a v podstatě kdekoliv, kde se něco staví.
Při práci s úhly je první krok základní poznávání úhlů – potřebujeme získat základní představu o úhlech a schopnost odhadnout velikost úhlu podle obrázku. Další krok je pak znalost pojmů souvisejících s úhly, mezi které patří třeba úhel ostrý, tupý, pravý, plný, vrcholový či střídavý.
Jakmile zvládneme základy práce s úhly, můžeme se pustit do práce s úhly v rovinných objektech:
Pokročilejší téma pak jsou radiány, což je alternativní vyjadřování velikosti úhlů, které se často používá ve spojitosti s goniometrickými funkcemi.
Úhly a želvy
Pro získání zběhlosti v práci s úhly může posloužit atraktivní cvičení Želví grafika zařazené v předmětu informatika.
Úhly v trojúhelníku
Při výpočtu velikosti neznámého úhlu v trojúhelníku využíváme základní vlastnosti, že součet vnitřních úhlů v trojúhelníku je 180°.
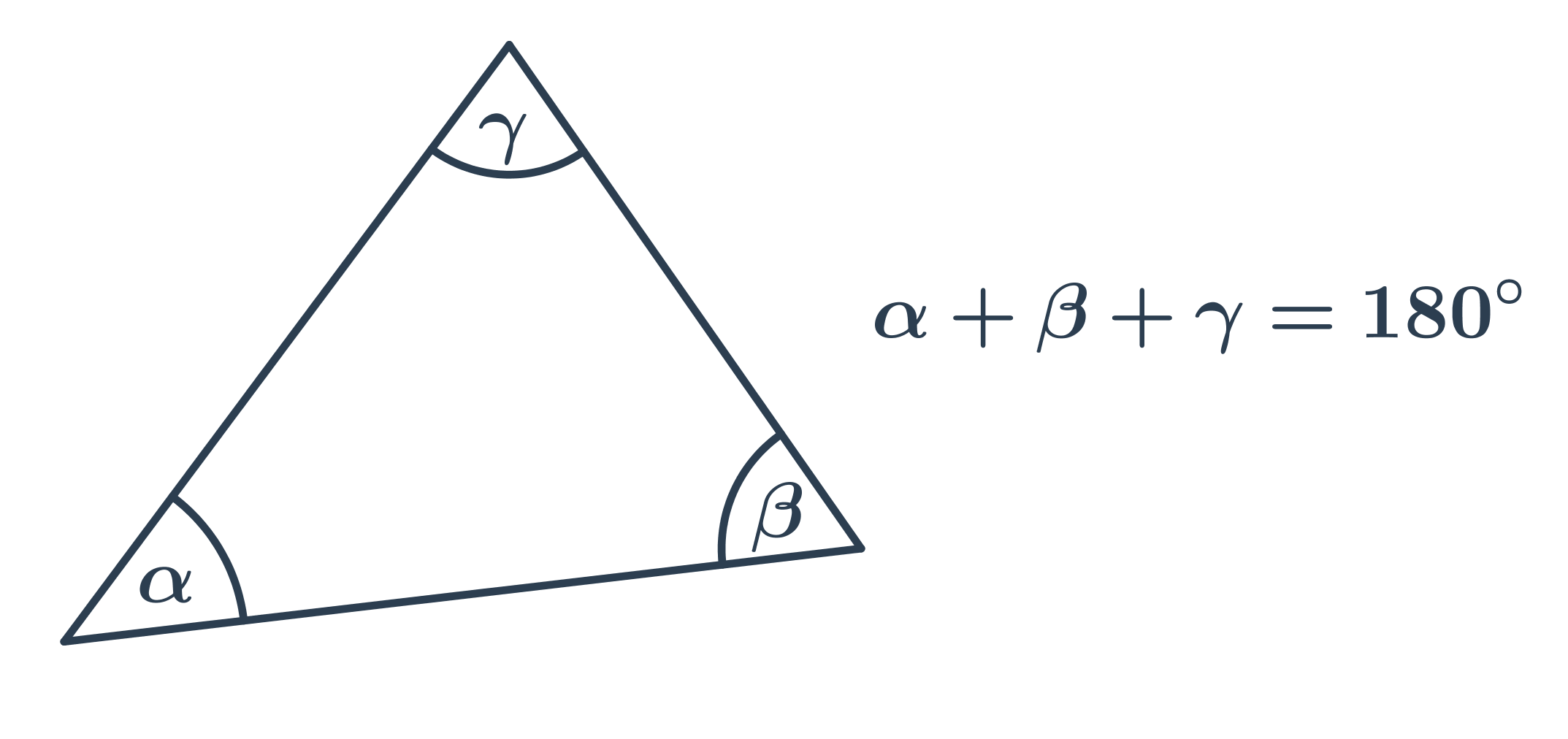
Speciální případy:
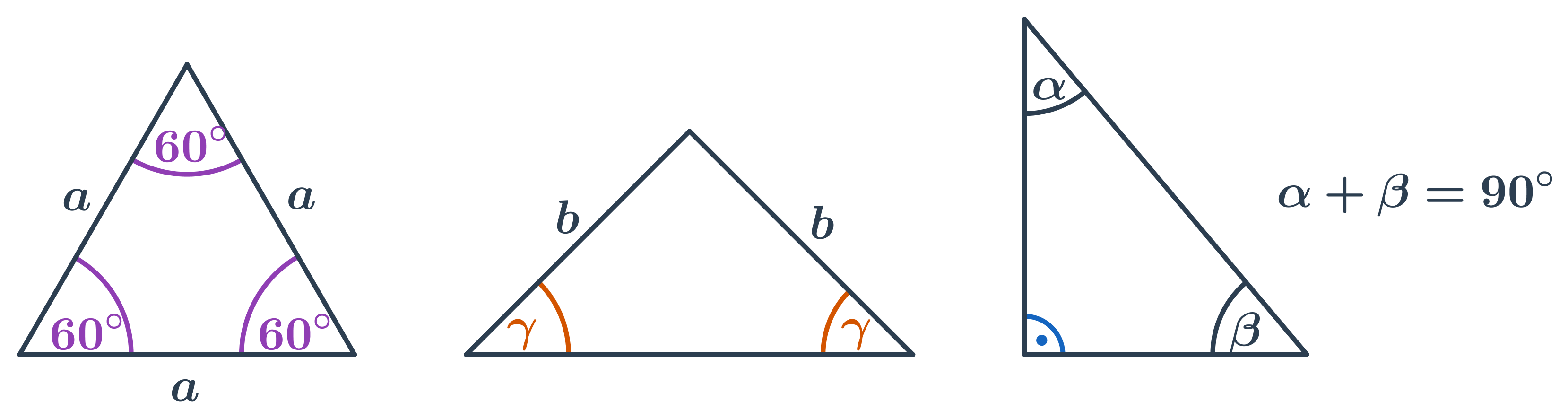
- V rovnostranném trojúhelníku mají všechny vnitřní úhly velikost 60°.
- V rovnoramenném trojúhelníku jsou oba úhly u základny stejné.
- V pravoúhlém trojúhelníku je velikost jednoho úhlu 90°, součet velikostí zbývajících dvou úhlů je také 90°.
Při výpočtu lze využít i vrcholových a vedlejších úhlů.
Příklad: výpočet velikosti úhlu
Určete velikost oranžového úhlu:
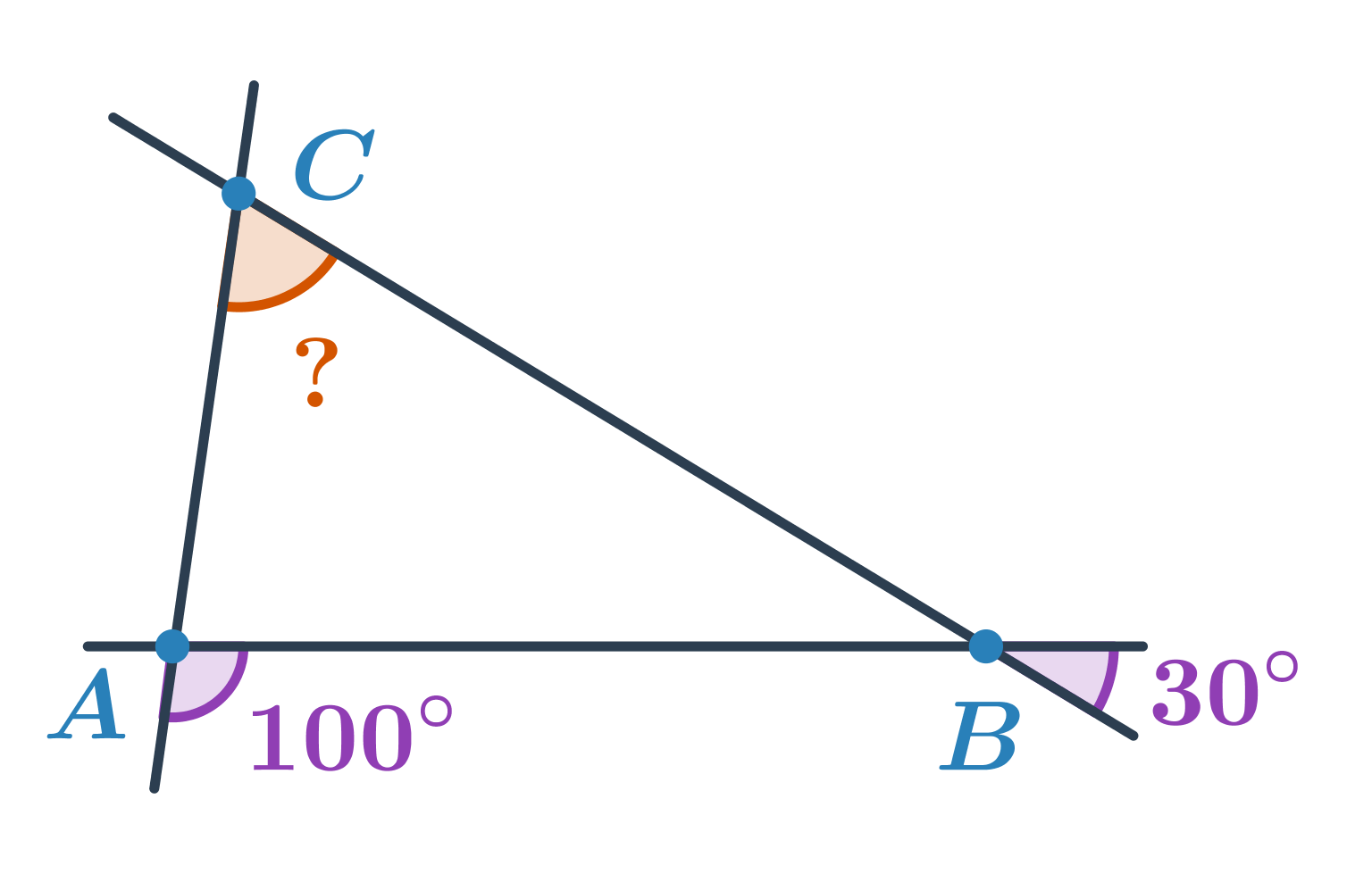
- Úhel u vrcholu B tvoří s úhlem o velikosti 30° dvojici vrcholových úhlů. Jeho velikost je tedy 30°.
- Úhel u vrcholu A tvoří s úhlem o velikosti 100° dvojici vedlejších úhlů. Jeho velikost je tedy 180°-100°=80°.
- Pro velikost neznámého úhlu u vrcholu C pak platí: 180°-80°-30°=70°
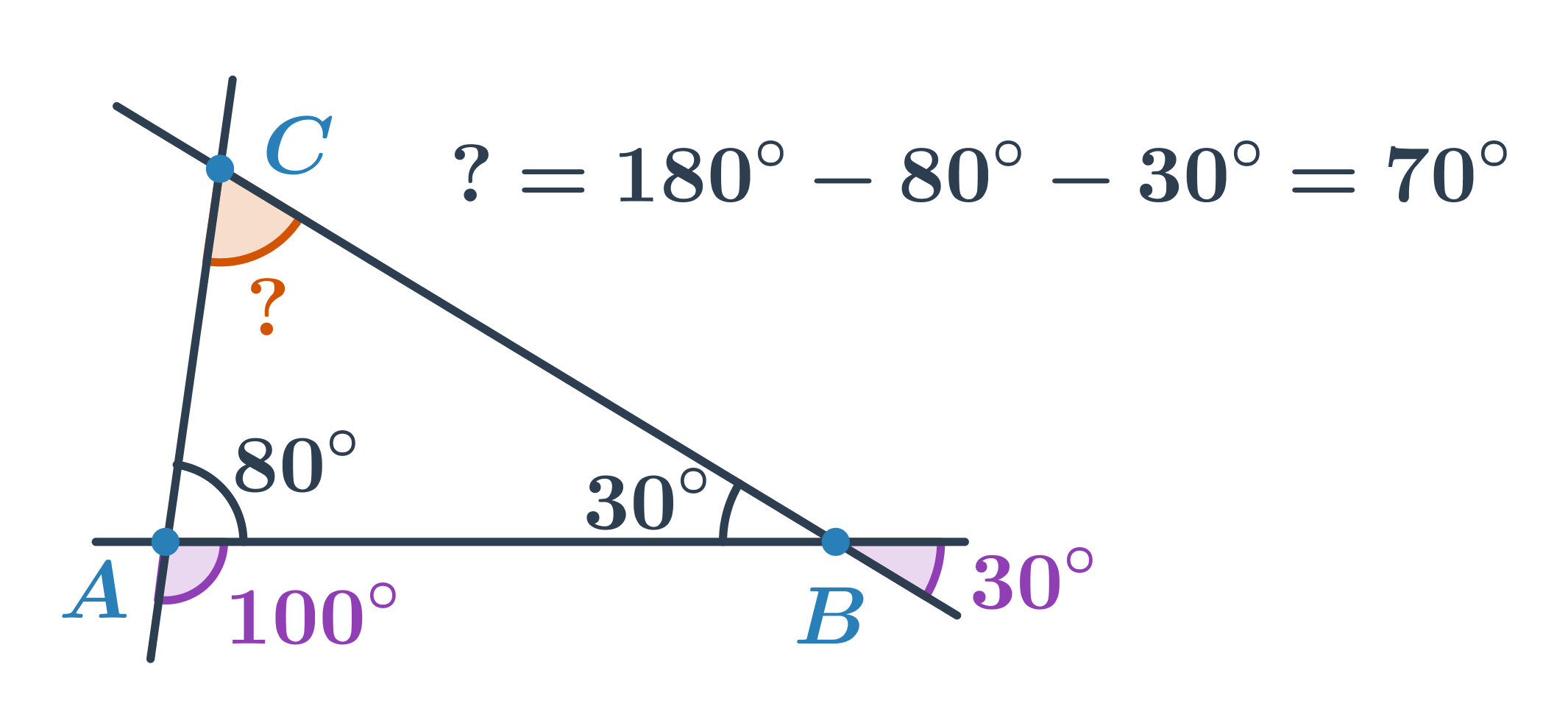
Úhly ve čtyřúhelníku
Součet vnitřních úhlů ve čtyřúhelníku je 360°.
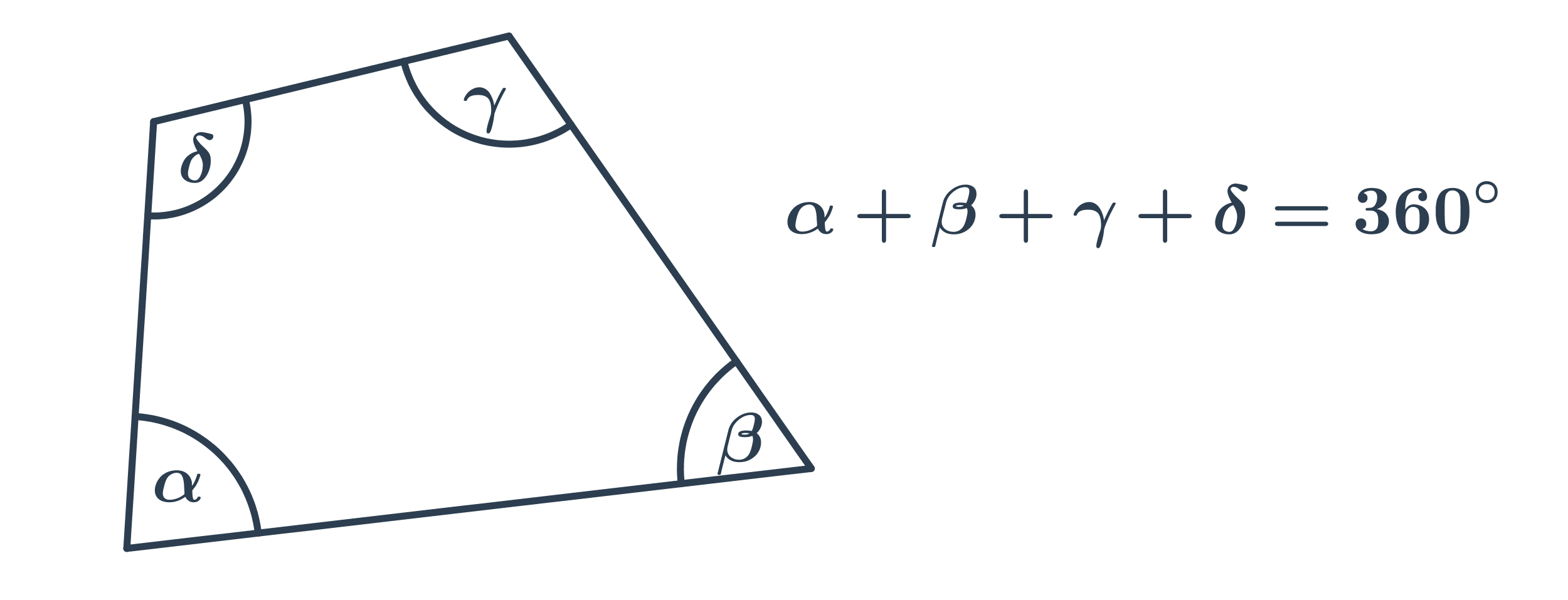
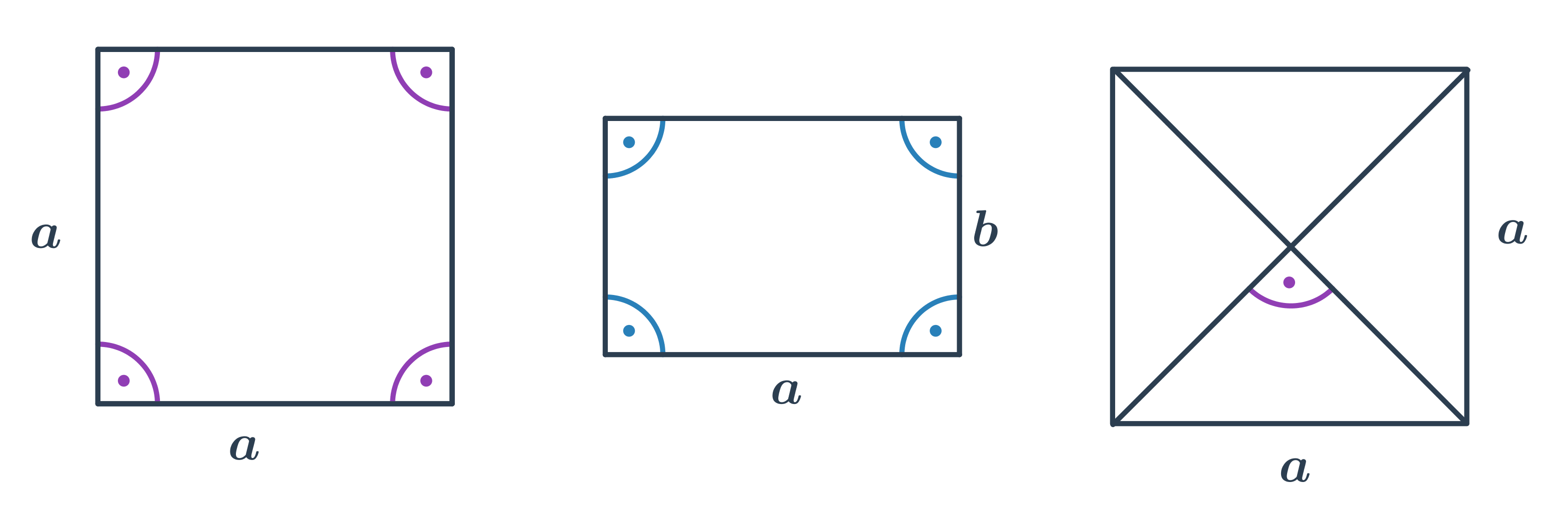
Čtverec, obdélník
- Ve čtverci i obdélníku je velikost všech vnitřních úhlů 90°.
- Ve čtverci svírají úhlopříčky úhel o velikosti 90°.
Rovnoběžník
- Protější úhly mají stejnou velikost.
- Součet velikostí sousedních úhlů je 180°.
- Speciálním případem rovnoběžníku je kosočtverec, jehož úhlopříčky svírají pravý úhel.
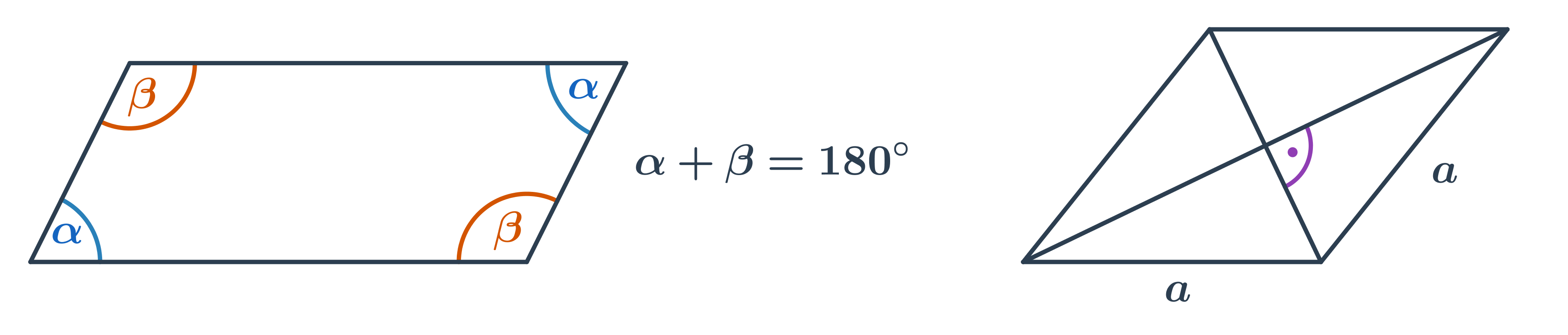
Lichoběžník
- Součet velikostí vnitřních úhlů u ramen je 180°.
- V rovnoramenném lichoběžníku jsou úhly u základen shodné.
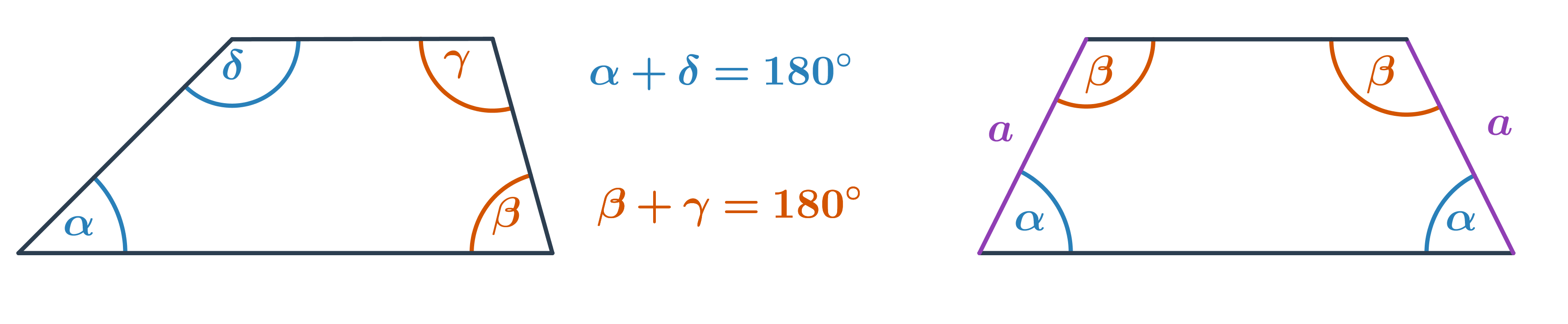
Při výpočtu neznámého úhlu můžeme také daný čtyřúhelník rozdělit na několik trojúhelníků a lze využít i vrcholových a vedlejších úhlů.
Příklad: určete velikost úhlu
Určete velikost oranžového úhlu v rovnoběžníku ABCD.
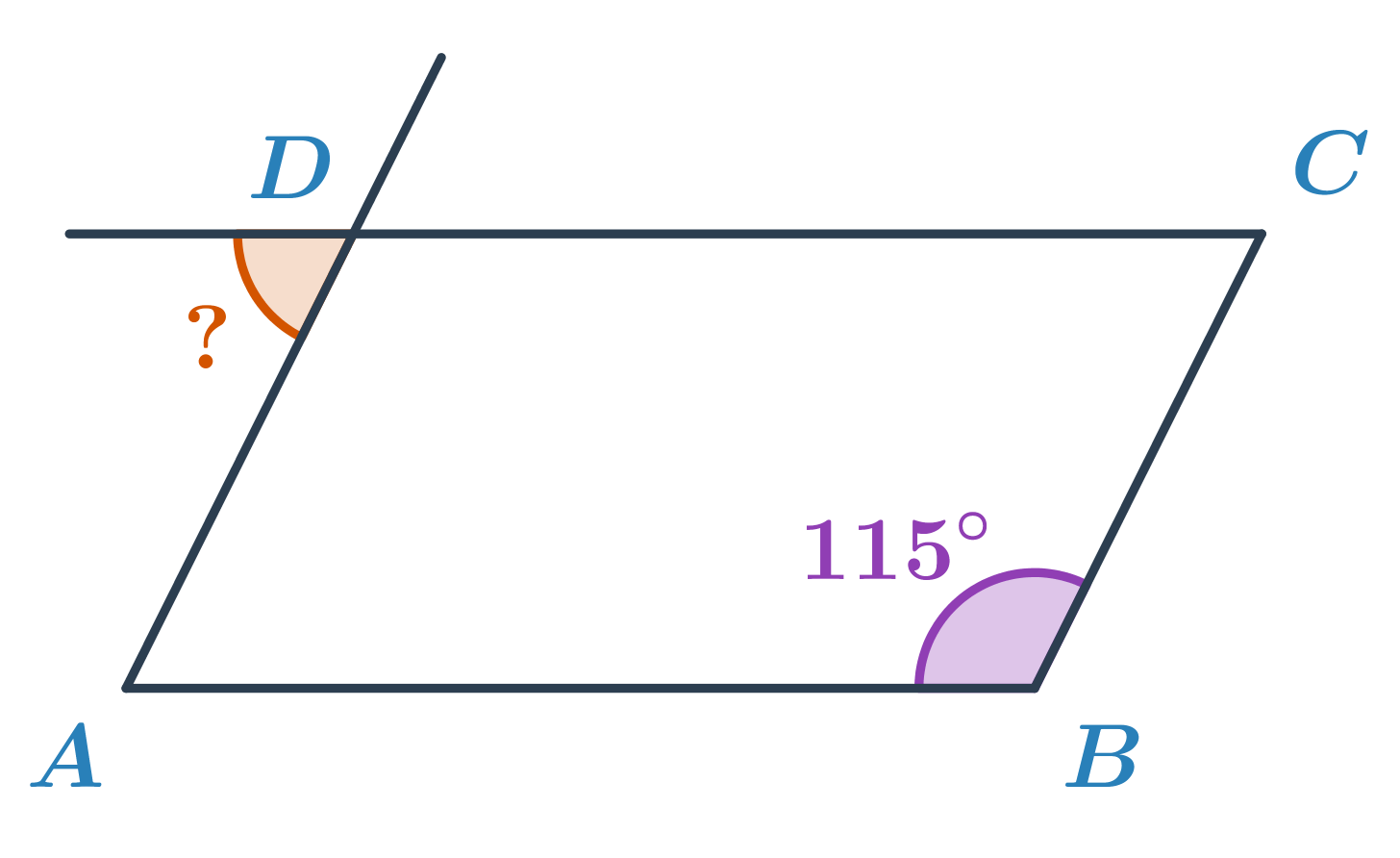
V rovnoběžníku mají protější úhly stejnou velikost, úhel ADC má tedy velikost 115°. Úhel ADC tvoří s neznámým úhlem dvojici vedlejších úhlů. Velikost neznámého úhlu je tedy 180°-115°=65°.
Úhly a mnohoúhelníky
Součet vnitřních úhlů v obecném mnohoúhelníku s n stranami (tedy n-úhelníku) je 180^\circ\cdot(n-2). Například v pětiúhelníku je součet vnitřních úhlů 180^\circ(5-2)=540^\circ. Každý vnitřní úhel pak může mít jinou velikost.
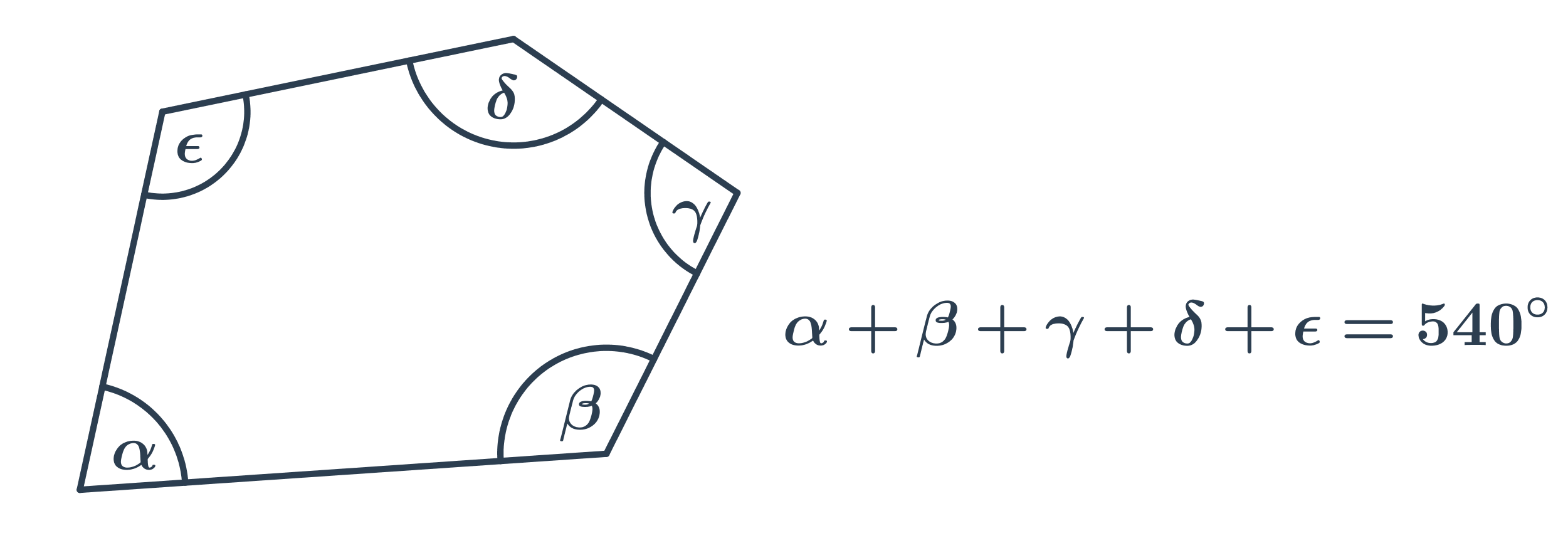
Pravidelné mnohoúhelníky
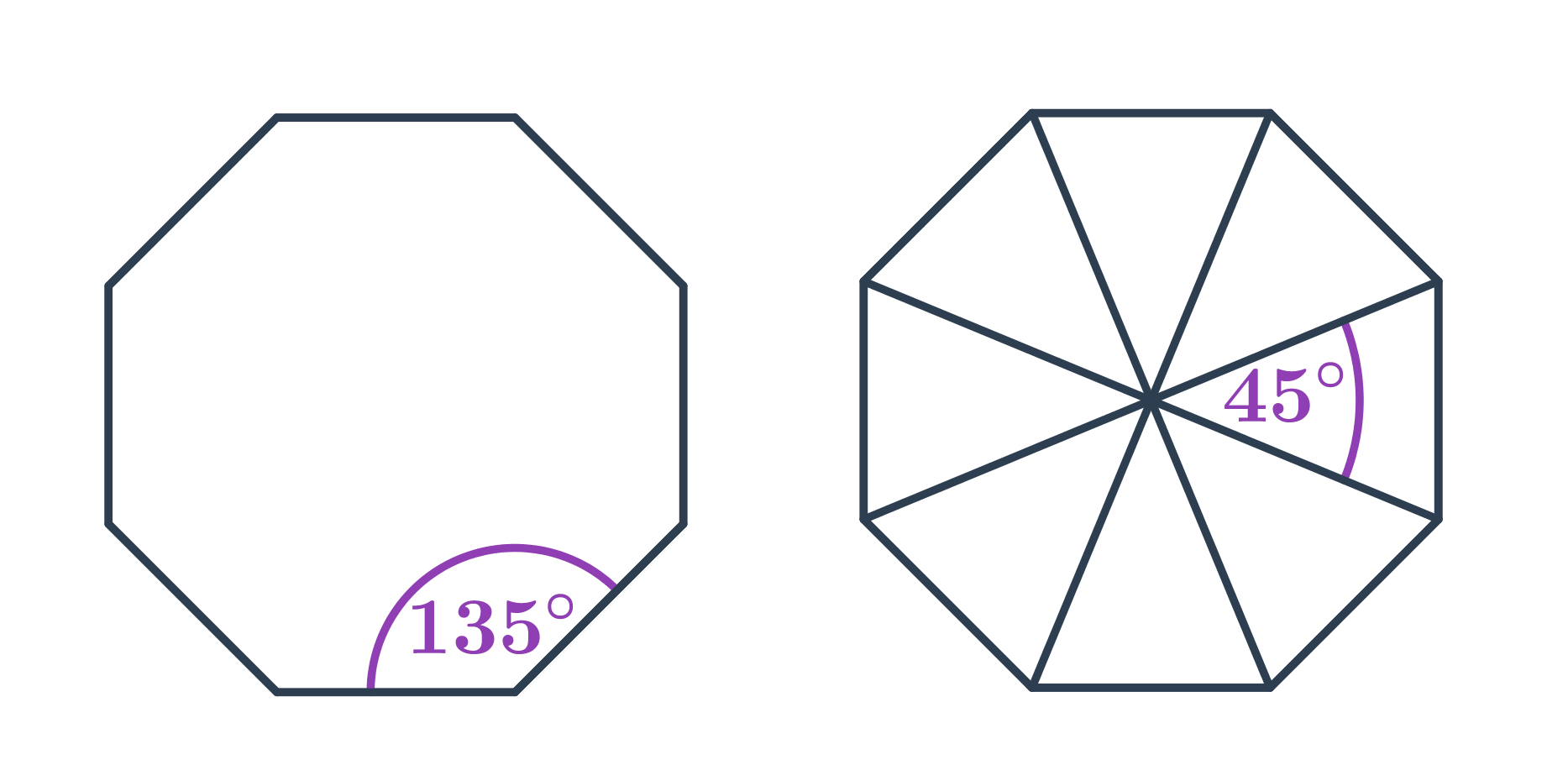
- Každý vnitřní úhel v pravidelném mnohoúhelníku s n vrcholy má velikost 180^\circ\cdot\frac{n-2}{n}. Například v pravidelném osmiúhelníku má každý vnitřní úhel velikost 180^\circ\cdot\frac{8-2}{6}=135^\circ.
- Velikost středového úhlu pravidelného n-úhelníku je \frac{360^\circ}{n}. Například v pravidelném osmiúhelníku má každý středový úhel velikost \frac{360^\circ}{8}=45^\circ.
Při výpočtu neznámého úhlu v mnohoúhelníku lze využít i vrcholových a vedlejších úhlů.
Příklad: Určete velikost úhlu
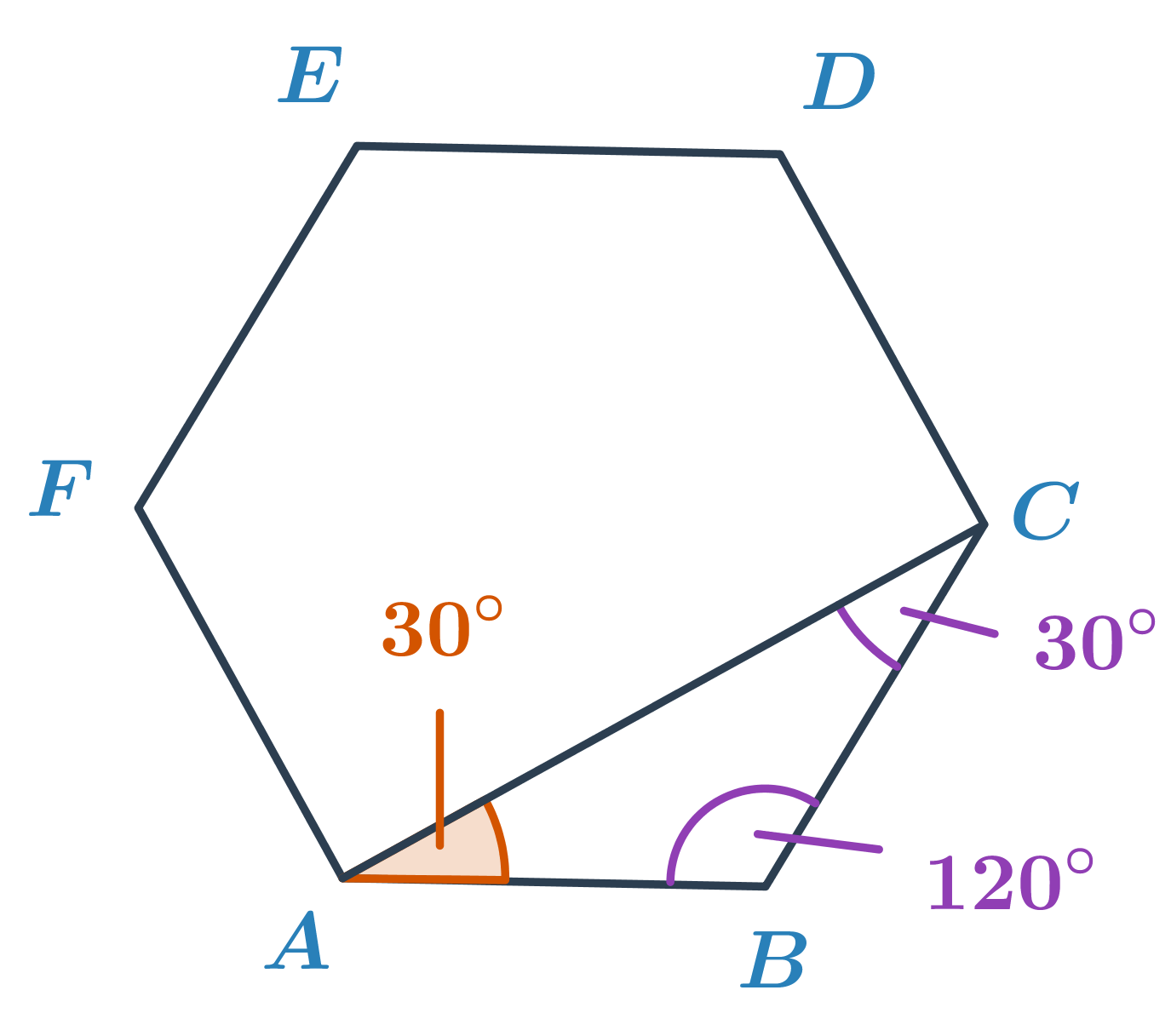
Určete velikost oranžového úhlu v pravidelném šestiúhelníku ABCDEF.
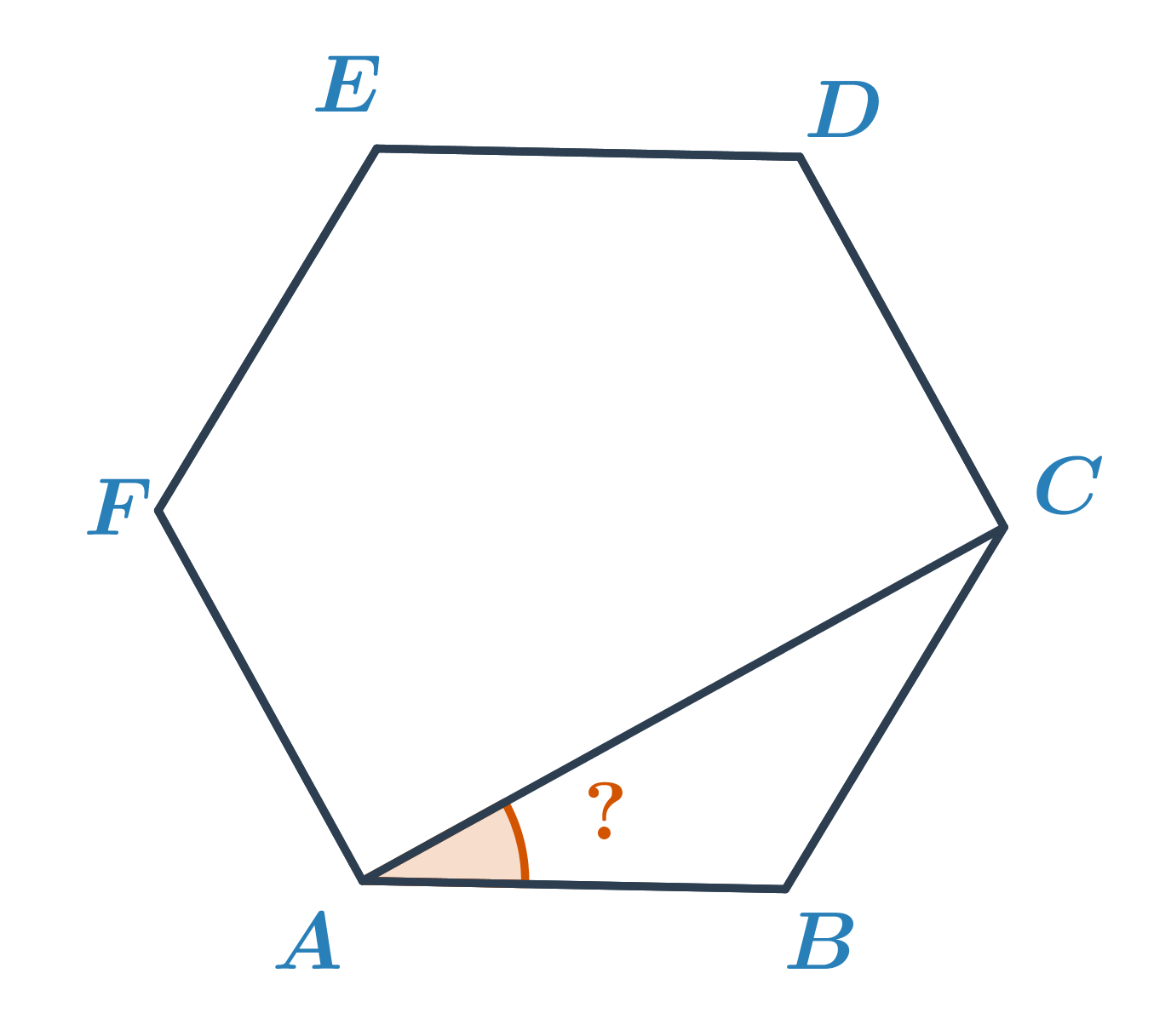
V pravidelném šestiúhelníku má každý úhel stejnou velikost, a to 180^\circ\cdot\frac{6-2}{6}=120^\circ. Úhel ABC má tedy velikost 120^\circ. Trojúhelník ABC je rovnoramenný, úhly u vrcholů A a C jsou pak shodné. Jejich velikost je (180^\circ-120^\circ):2=30^\circ.
Úhly a kružnice
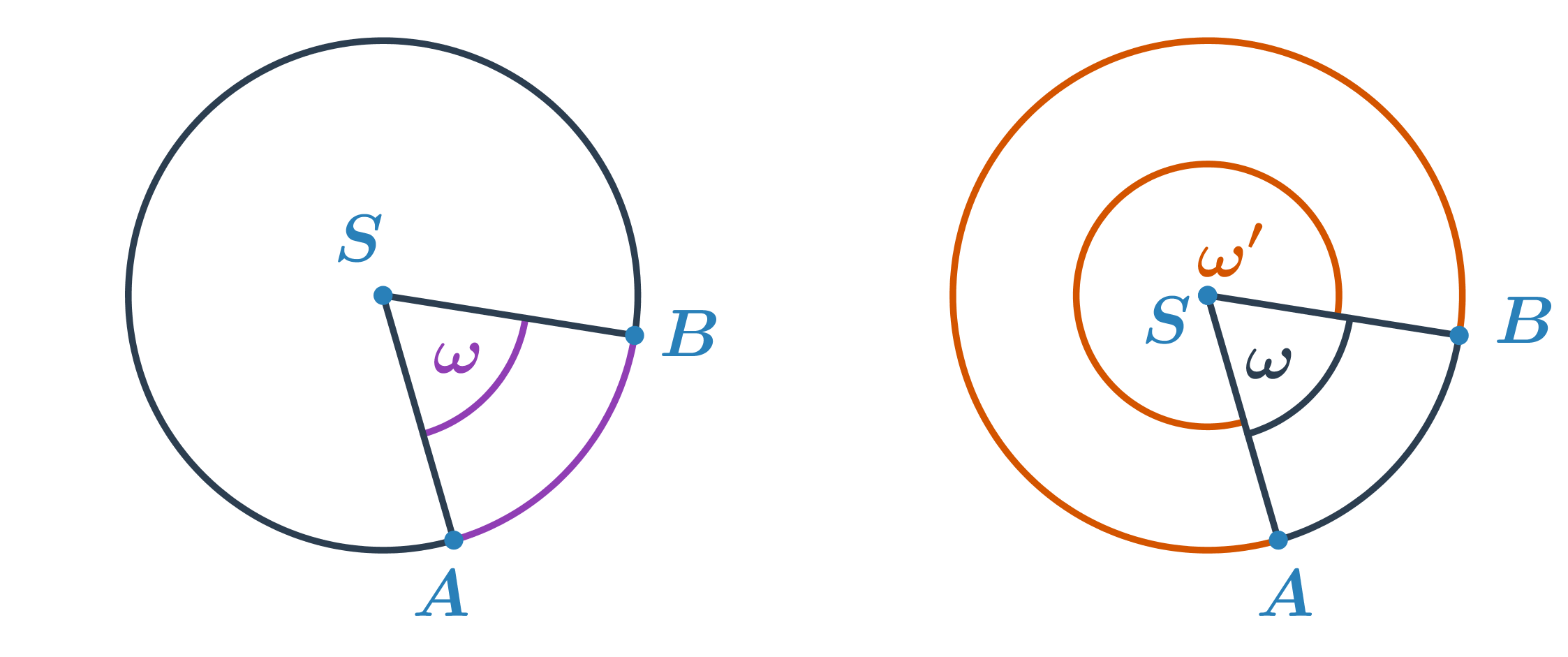
Středový úhel
- Úhel s vrcholem ve středu S kružnice k, jehož ramena procházejí krajními body A, B oblouku kružnice k.
- Pro každé dva body na kružnici lze určit dva středové úhly. Každý přísluší tomu oblouku, který v daném úhlu leží.
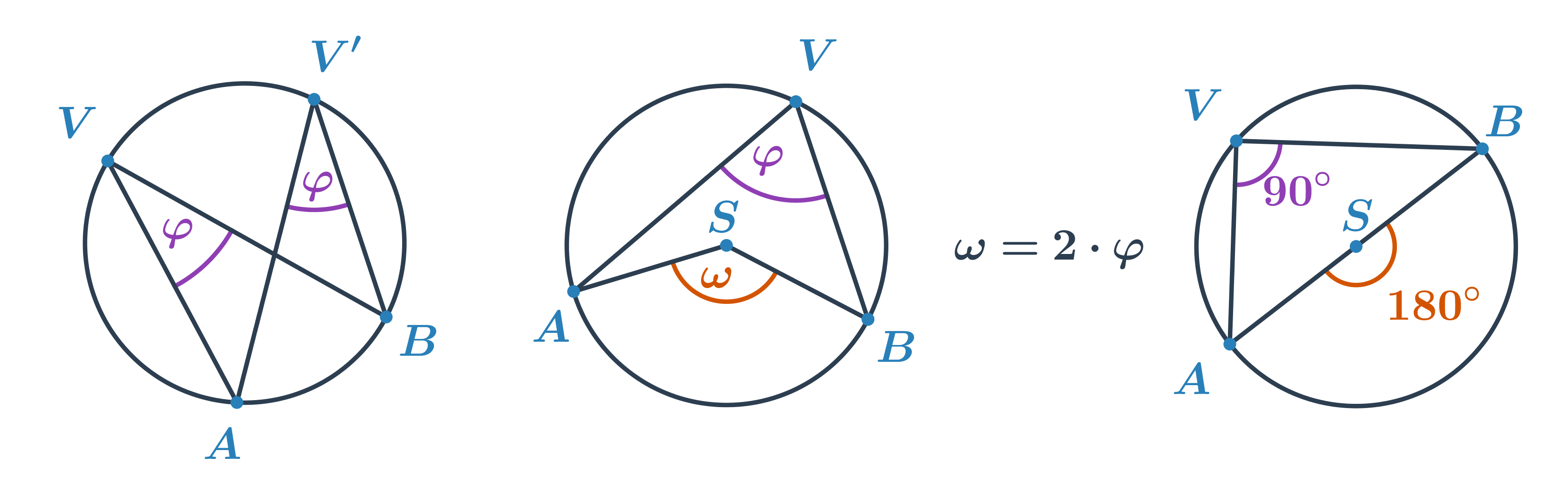
Obvodový úhel
- Úhel, jehož vrchol V leží na kružnici k a jeho ramena procházejí body A, B oblouku kružnice k (A \neq V \neq B)
- Všechny obvodové úhly příslušné oblouku AB s vrcholem V, který na oblouku neleží, mají stejnou velikost.
- Velikost středového úhlu \omega se rovná dvojnásobku velikosti obvodového úhlu \varphi příslušného ke stejnému oblouku, \omega = 2\cdot\varphi.
- Thaletova věta: Obvodový úhel nad průměrem kružnice je pravý.
Úsekový úhel
- Úhel, jenž svírá tětiva AB kružnice k s tečnou t kružnice v bodě A nebo B.
- Velikost úsekového úhlu je stejná jako velikost obvodového úhlu nad obloukem AB.
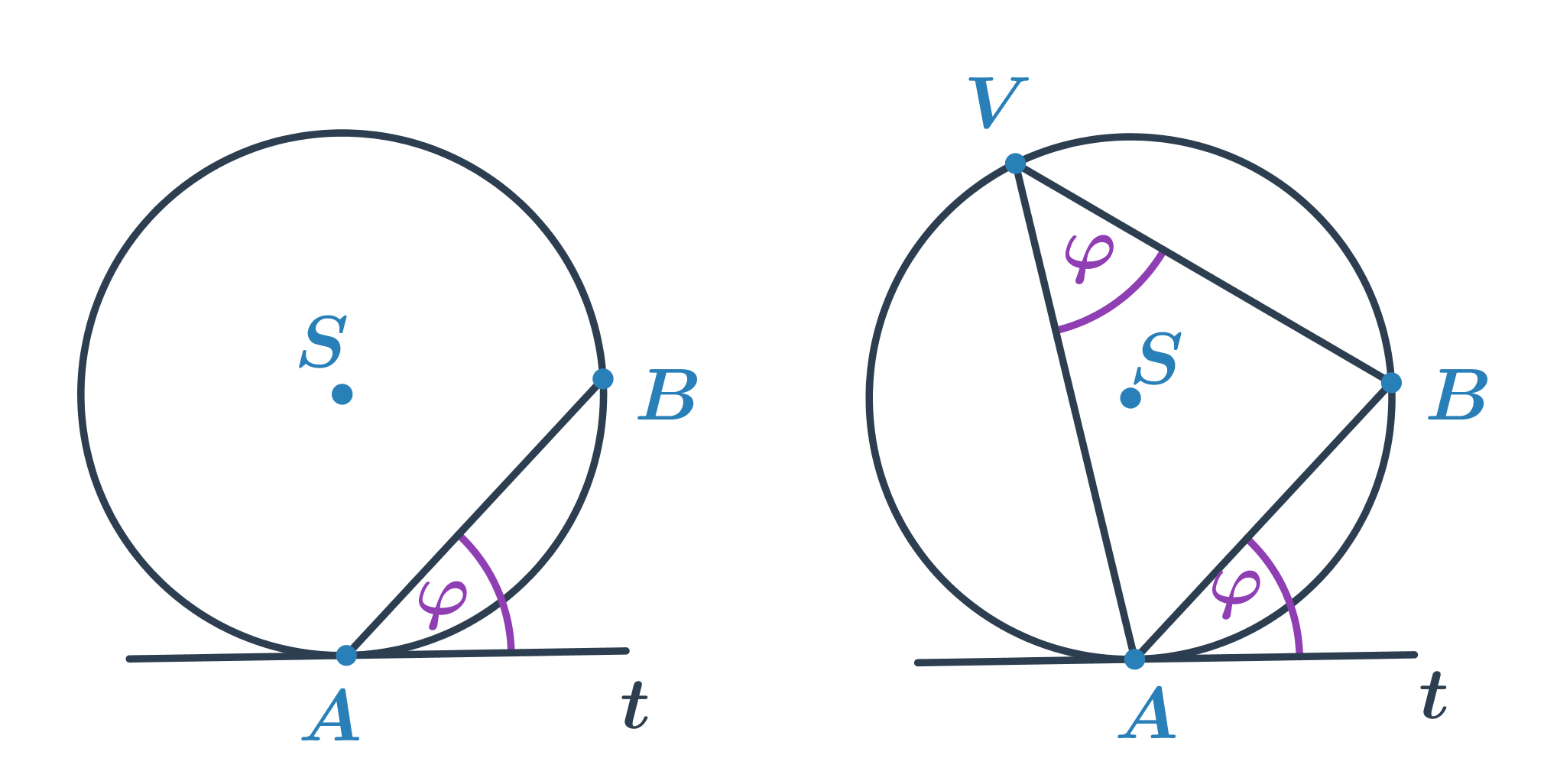
Příklad 1: Určete velikost úhlu
Určete velikost oranžového úhlu.
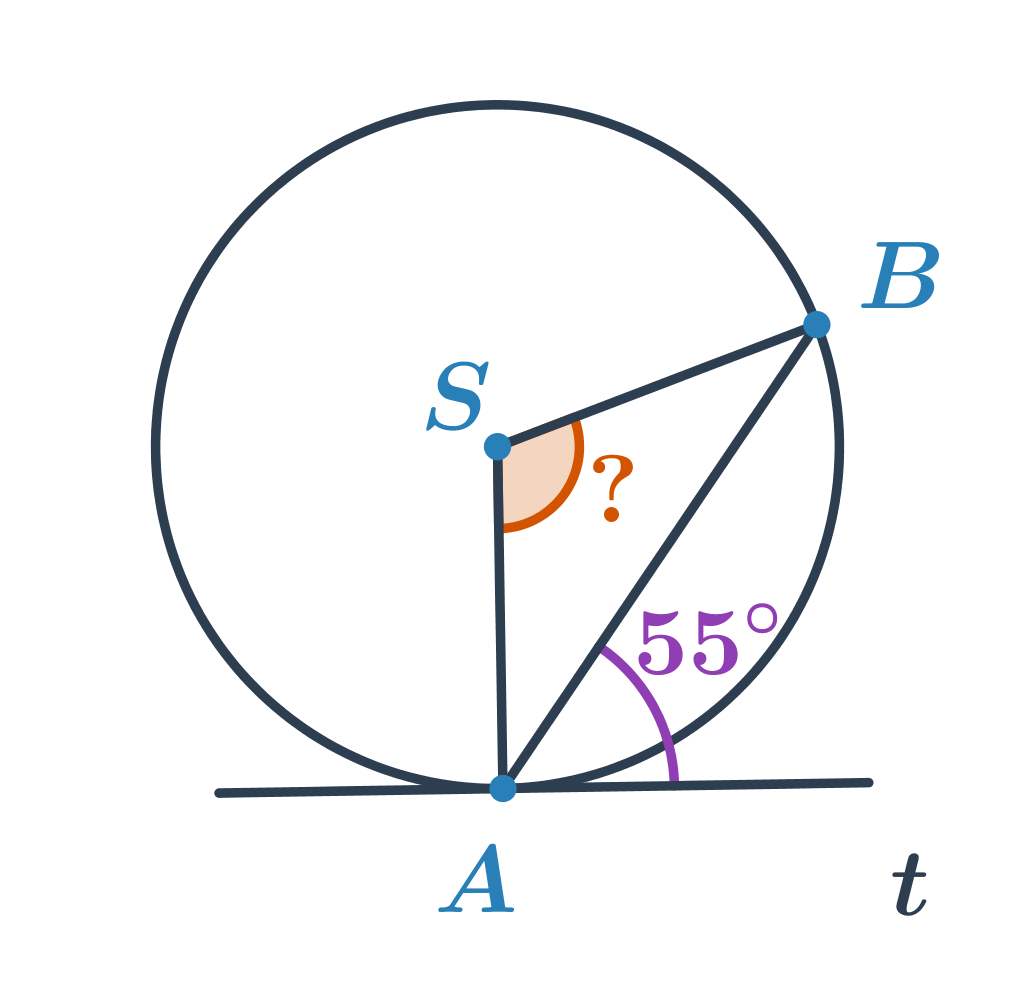
Úhel o velikosti 55^\circ je úsekový úhel příslušný tětivě AB. Víme, že velikosti úsekového a příslušného obvodového úhlu jsou stejné, tedy 55^\circ. Neznámý úhel je středový úhel příslušný menšímu oblouku AB. Jeho velikost je dvojnásobkem velikosti obvodového úhlu, tedy 2\cdot55^\circ=110^\circ.
Příklad 2: Určete velikost úhlu
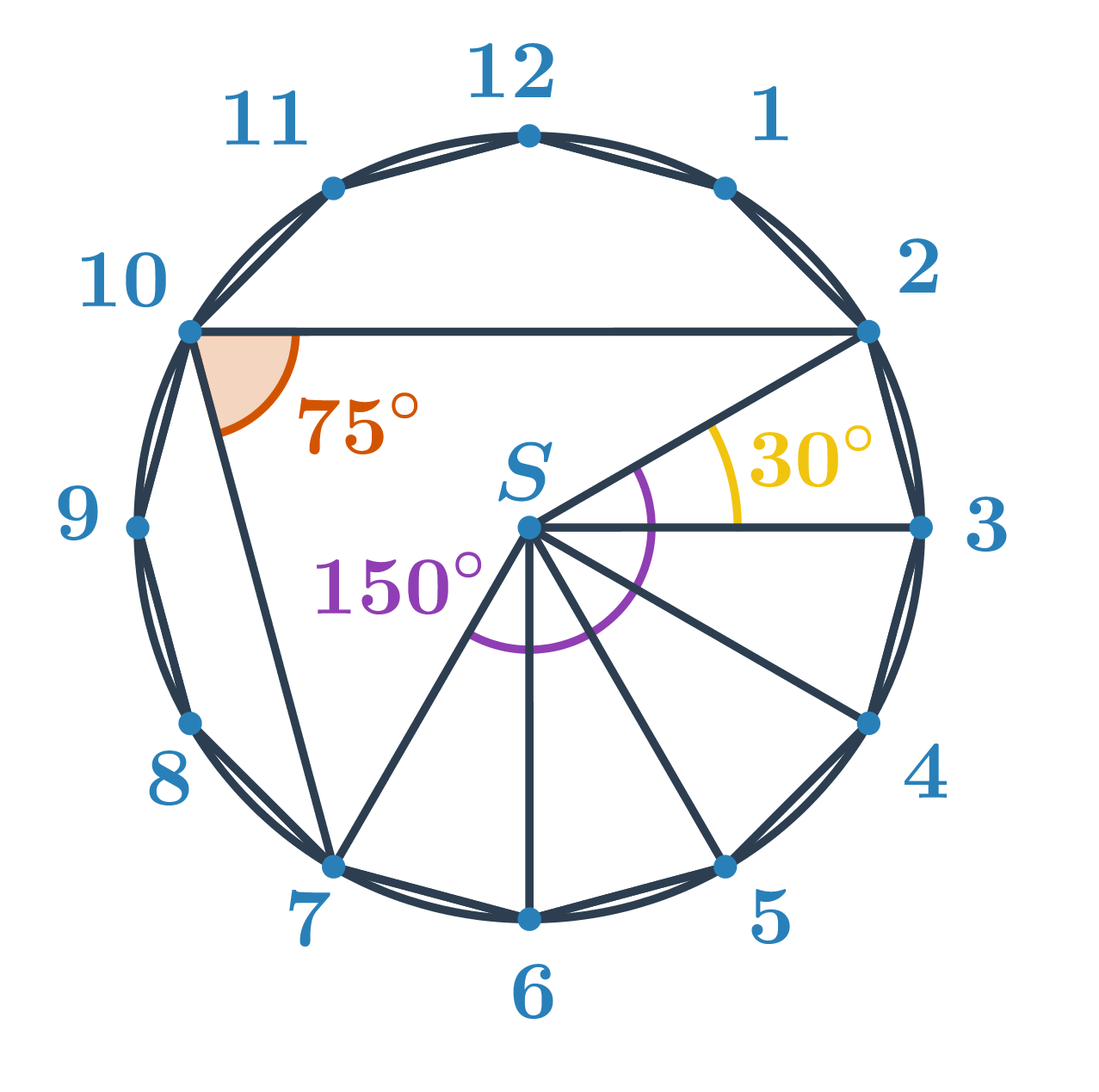
Určete velikost oranžového úhlu.
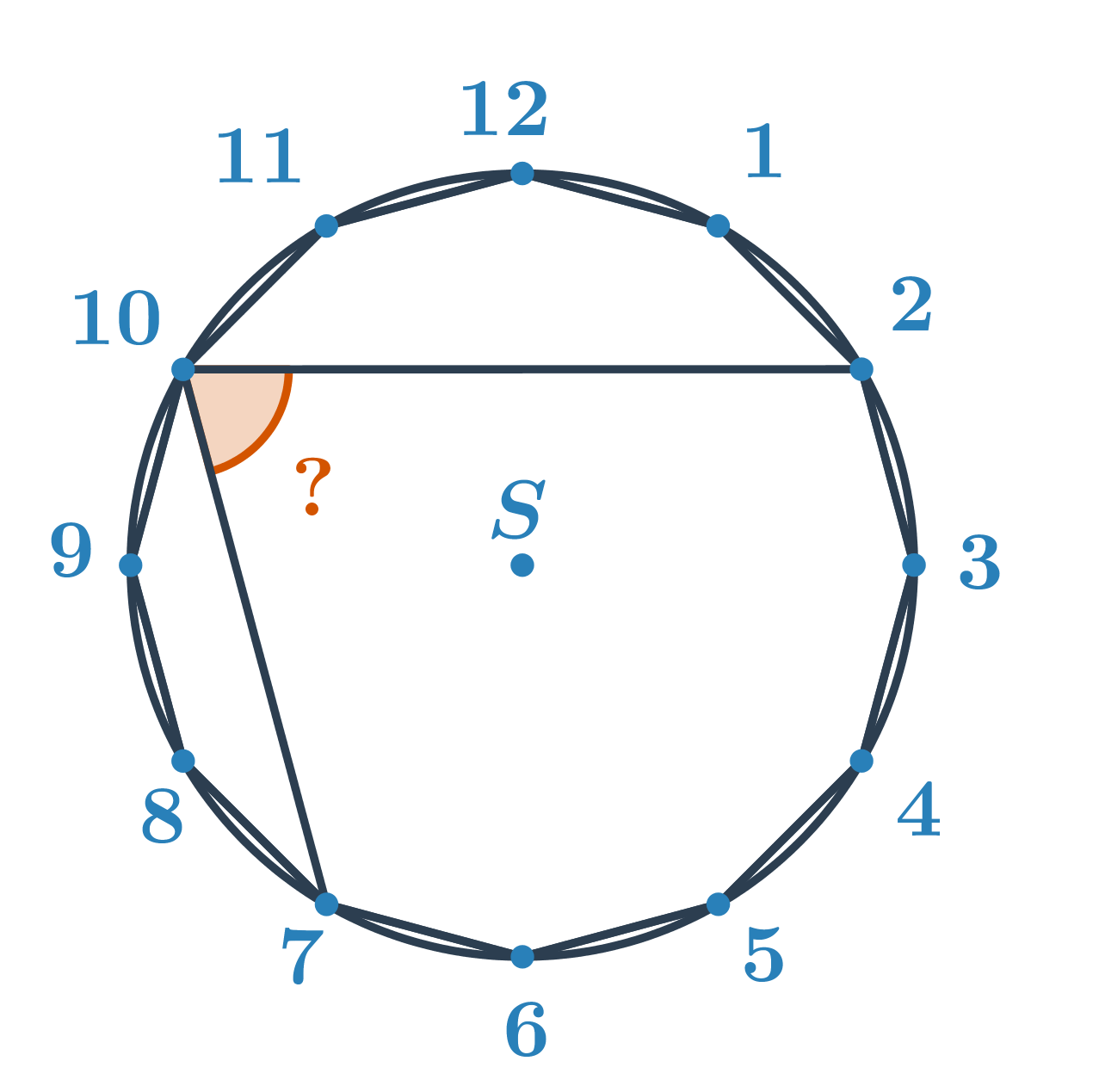
Neznámý úhel je obvodovým úhlem nad menším obloukem s koncovými body 2 a 7. Určíme velikost příslušného středového úhlu. Z kapitoly úhly a mnohoúhelníky víme, že velikost středového úhlu pravidelného n-úhelníku je \frac{360^\circ}{n}. Pro pravidelný dvanáctiúhelník je tedy úhel mezi spojnicemi dvou vedlejších vrcholů a středu \frac{360^\circ}{12}=30^\circ. Středový úhel příslušný oblouku 2 a 7 je pak 5\cdot30^\circ=150^\circ. Hledaný obvodový úhel má poloviční velikost, tedy 150^\circ:2=75^\circ.
Pojmy související s úhly
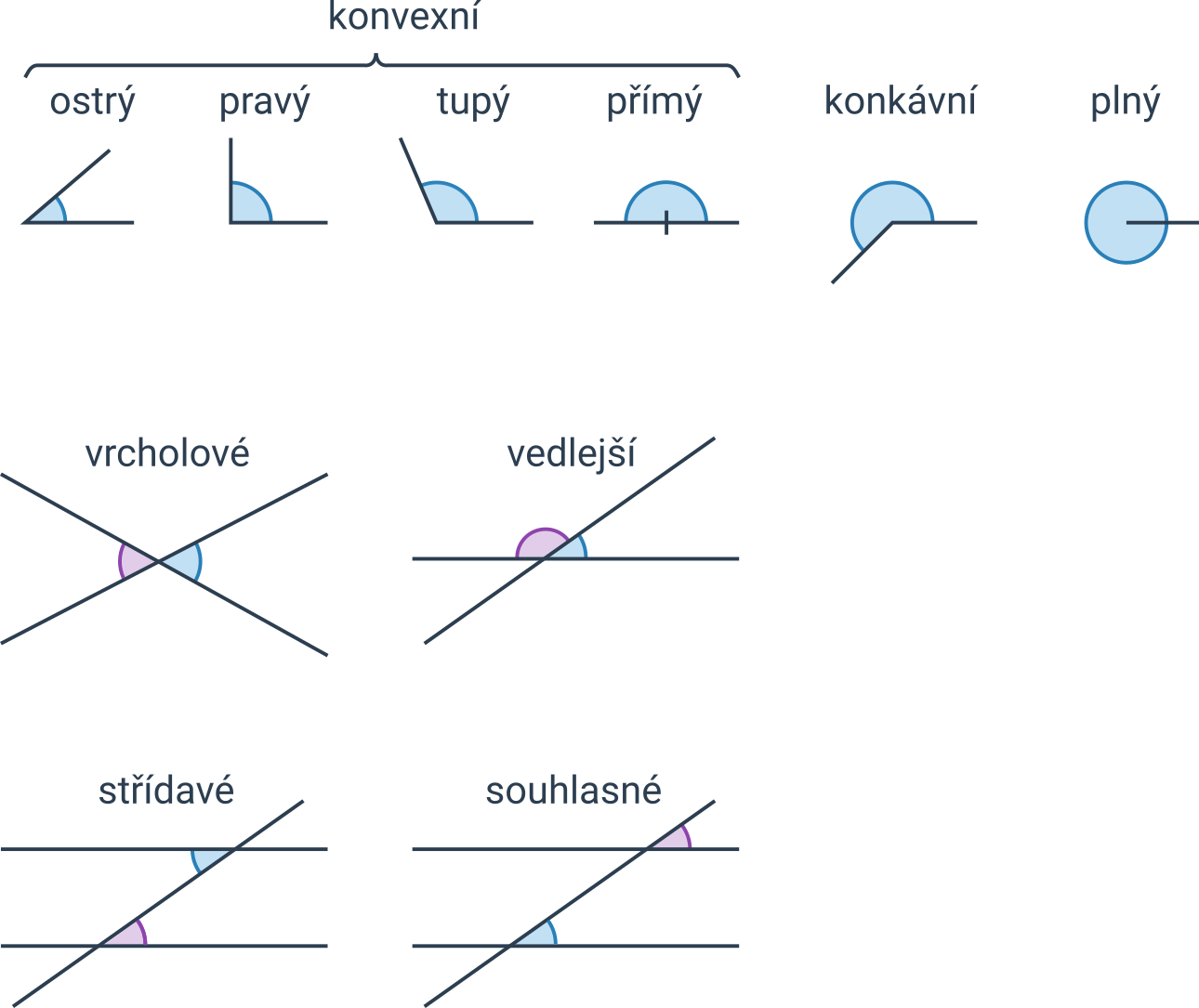
Úhly podle velikosti
| plný úhel | úhel o velikosti 360° |
| přímý úhel | úhel o velikosti 180° |
| pravý úhel | úhel o velikosti 90° |
| ostrý úhel | úhel menší než 90° |
| tupý úhel | úhel větší než 90° a menší než 180° |
| konvexní úhel | úhel menší nebo roven 180° |
| nekonvexní, konkávní úhel | úhel větší než 180° |
Pojmy související s dvojicemi úhlů
| vrcholové úhly | dvojice úhlů, jejichž ramena jsou opačné polopřímky | mají stejnou velikost |
| vedlejší úhly | dvojice úhlů, jejichž jedno rameno je společné a druhá ramena jsou opačné polopřímky | součet jejich velikostí je 180° |
| souhlasné úhly | dvojice úhlů, jejichž první ramena leží na jedné přímce a druhá ramena jsou rovnoběžná, přitom směr příslušných ramen je stejný | mají stejnou velikost |
| střídavé úhly | dvojice úhlů, jejichž první ramena leží na jedné přímce a druhá ramena jsou rovnoběžná, přitom směr příslušných ramen je opačný | mají stejnou velikost |