Povrch

Povrch kvádru s délkami hran a,b,c spočítáme jako součet obsahů všech jeho stěn. Tedy: S=2 (a\cdot b + a\cdot c + b \cdot c)

Povrch krychle s délkou hrany podstavy a spočítáme stejným způsobem, jako objem kvádru s a=b=c, tedy šestkrát obsah jedné čtvercové stěny krychle: S = 6\cdot a\cdot a = 6a^2

Povrch hranolu, který má podstavu o obsahu S_p plášť o obsahu S_{pl}, spočítáme jako S=2S_p + S_{pl}. Plášť hranolu je tvořen všemi jeho stěnami kromě dvou podstav.

Povrch pravidelného n‑bokého hranolu, který má dvě podstavy ve tvaru pravidelných n‑úhelníků a potom n stejných obdélníkových stěn (obsah jedné označme S_1), spočítáme takto: S=2S_p + n\cdot S_1

Povrch jehlanu spočítáme jako součet obsahu jeho podstavy S_p a obsahu jeho pláště S_{pl}. Obsah pláště spočítáme jako součet obsahů stěn jehlanu, které tvoří plášť (tj. všechny stěny jehlanu kromě jeho podstavy).

Povrch pravidelného n‑bokého jehlanu, který má podstavu ve tvaru pravidelného n‑úhelníka a potom n stejných trojúhelníkových stěn (obsah jedné označme S_1), spočítáme takto: S= S_p + n\cdot S_1

Povrch „hranatých“ těles je prostě součet obsahů jednotlivých stran.

Hranol má dvě stejné podstavy a plášť, povrch je tedy S=2\cdot S_p+S_{pl}. Jehlan má jednu podstavu a plášť, povrch je tedy S=S_p+S_{pl}.

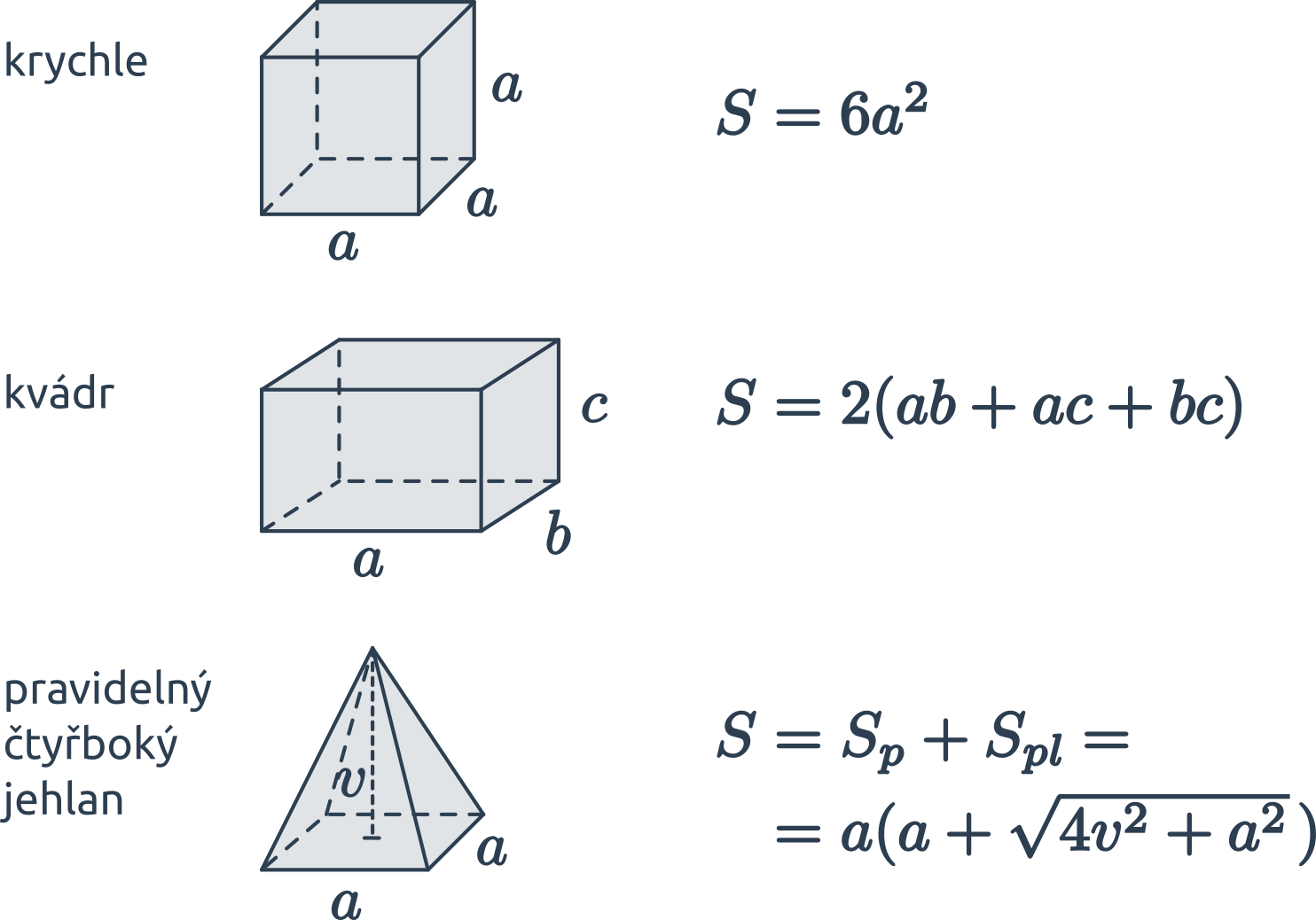
Stěny kvádru jsou obdélníky, přičemž vždy dvě jsou stejně velké. Povrch tedy vypočítáme jako S = 2(ab+ac+bc).

Krychle má šest stěn a všechny jsou tvořeny stejným čtvercem. Povrch je S=6a^2.

Povrch válce s poloměrem podstavy r a výškou v spočítáme jako: S = 2\pi r \cdot(r + v)

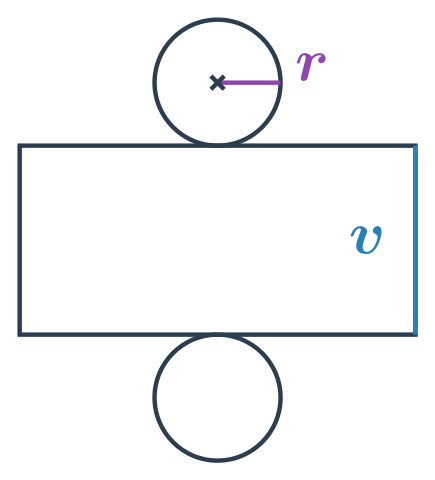
Platí S=2S_p + S_{pl}, kde S_p je obsah podstavy válce a S_{pl} obsah pláště válce. Podstava válce má tvar kruhu s poloměrem r a plášť válce je obdélník o stranách v a 2\pi r. Celkem máme:

• Obsah podstavy: S_p = \pi \cdot r^2
• Obsah pláště: S_{pl}=2\pi r \cdot v
• Povrch válce: S=2\pi r \cdot (r + v)

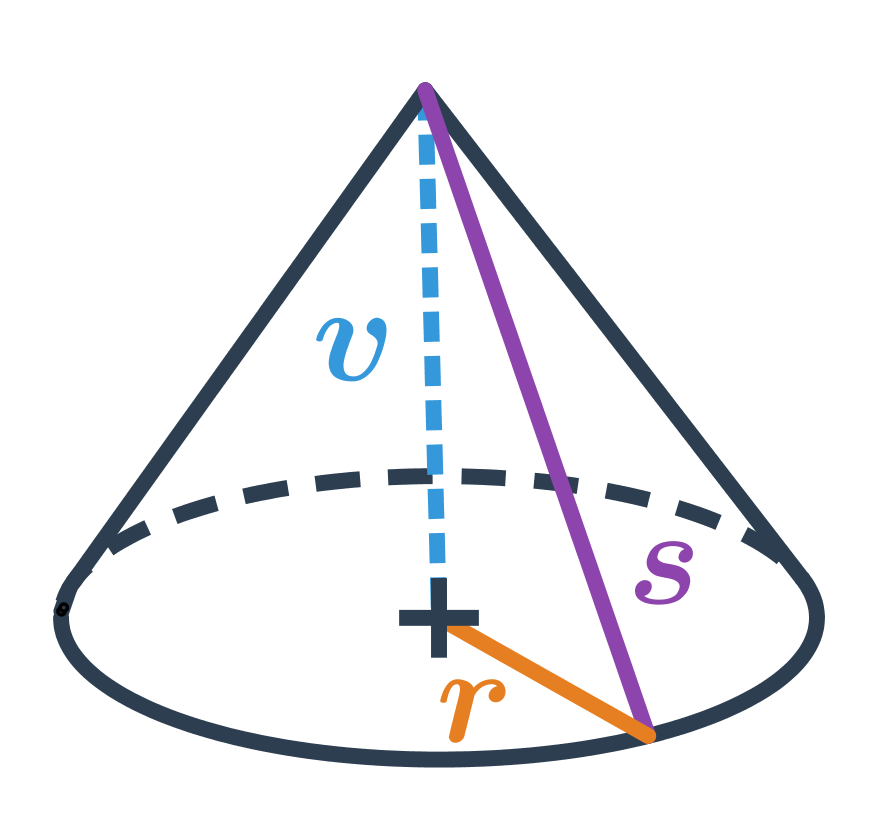
Může se stát, že známe poloměr r podstavy kužele a jeho výšku v, ale nemáme zadanou jeho stranu s. Potom si stranu můžeme dopočítat jako přeponu pravoúhlého trojúhelníka s odvěsnami o délkách v a r. Platí: s=\sqrt{v^2+r^2}

• Obsah podstavy kužele: \pi r^2
• Obsah pláště kužele: \frac{1}{2} \cdot 2 \pi r \cdot s = \pi r s

Povrch koule s poloměrem r spočítáme takto: S=4 \pi \cdot r^2

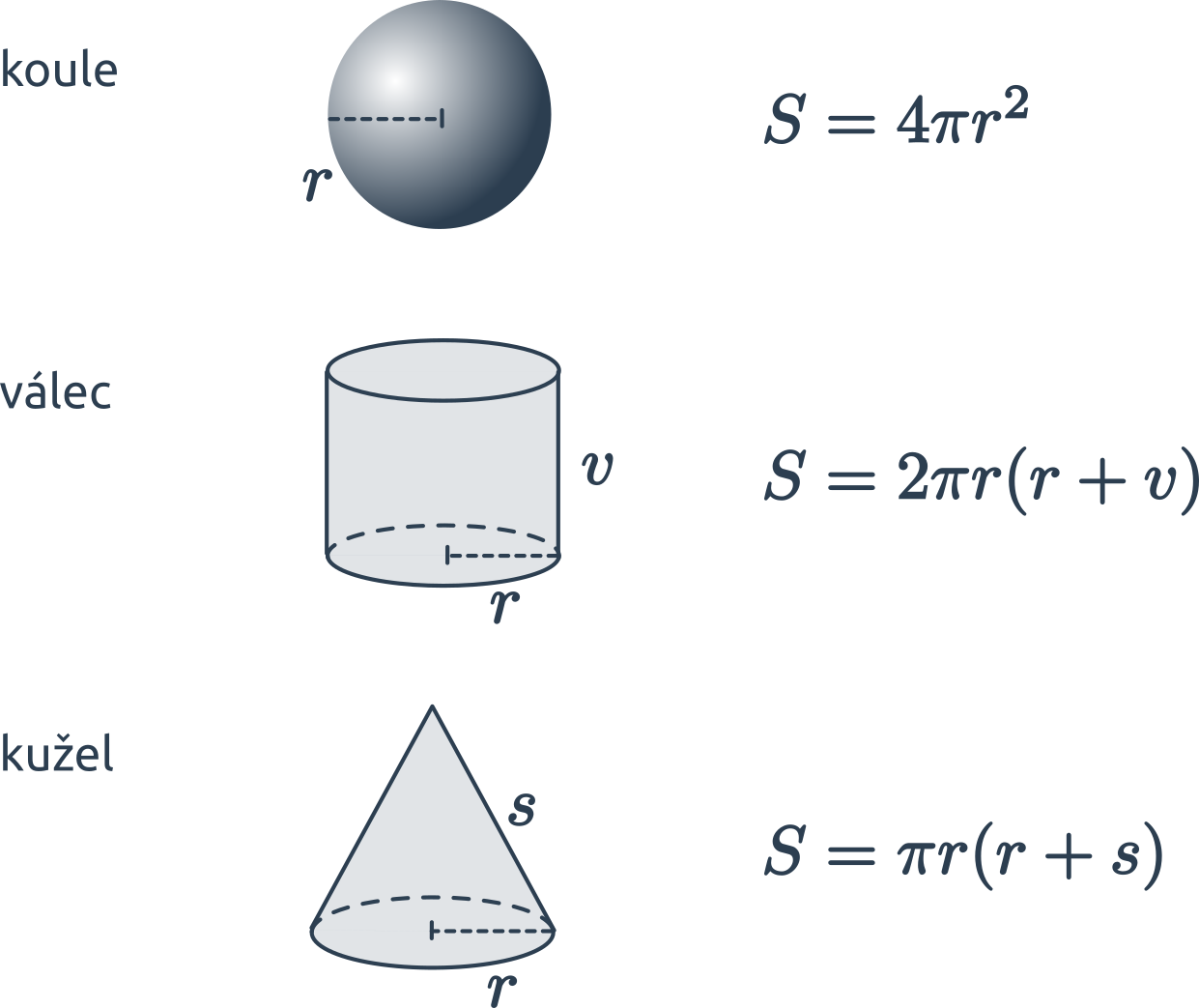
Povrch „kulatých“ těles vypočítáme za využití konstanty \pi \approx 3{,}14159265. Ve vzorcích označuje r poloměr (koule či podstavy), v výšku válce, s stranu kužele.

• Povrch koule je S = 4\pi r^2.
• Povrch válce se skládá z podstavy (dvakrát) a pláště: S = 2\cdot \pi r^2 + 2\pi r v = 2\pi r (r+v).
• Povrch kužele se skládá z podstavy a pláště: S = \pi r^2 + \pi rs= \pi r(r+s).