Výpis souhrnů
Obsah a obvod
Podtémata
Obsah a obvod
Obvod značíme o. Obvod je součet délek čar, které útvar vymezují. Se základním porozuměním tomu, co obvod vyjadřuje, pomůže téma délka a obvod na mřížce. Obvod se měří v jednotkách délky (např. centimetr, metr).
Obsah značíme S. Obsah vyjadřuje, kolik „místa v rovině“ útvar zaujímá. Se základním porozuměním tomu, co obsah vyjadřuje, pomůže téma obsah na mřížce. Obsah se měří v jednotkách obsahu (např. metr čtvereční, hektar).
Přehled vzorců pro obsah a obvod základních geometrických útvarů:
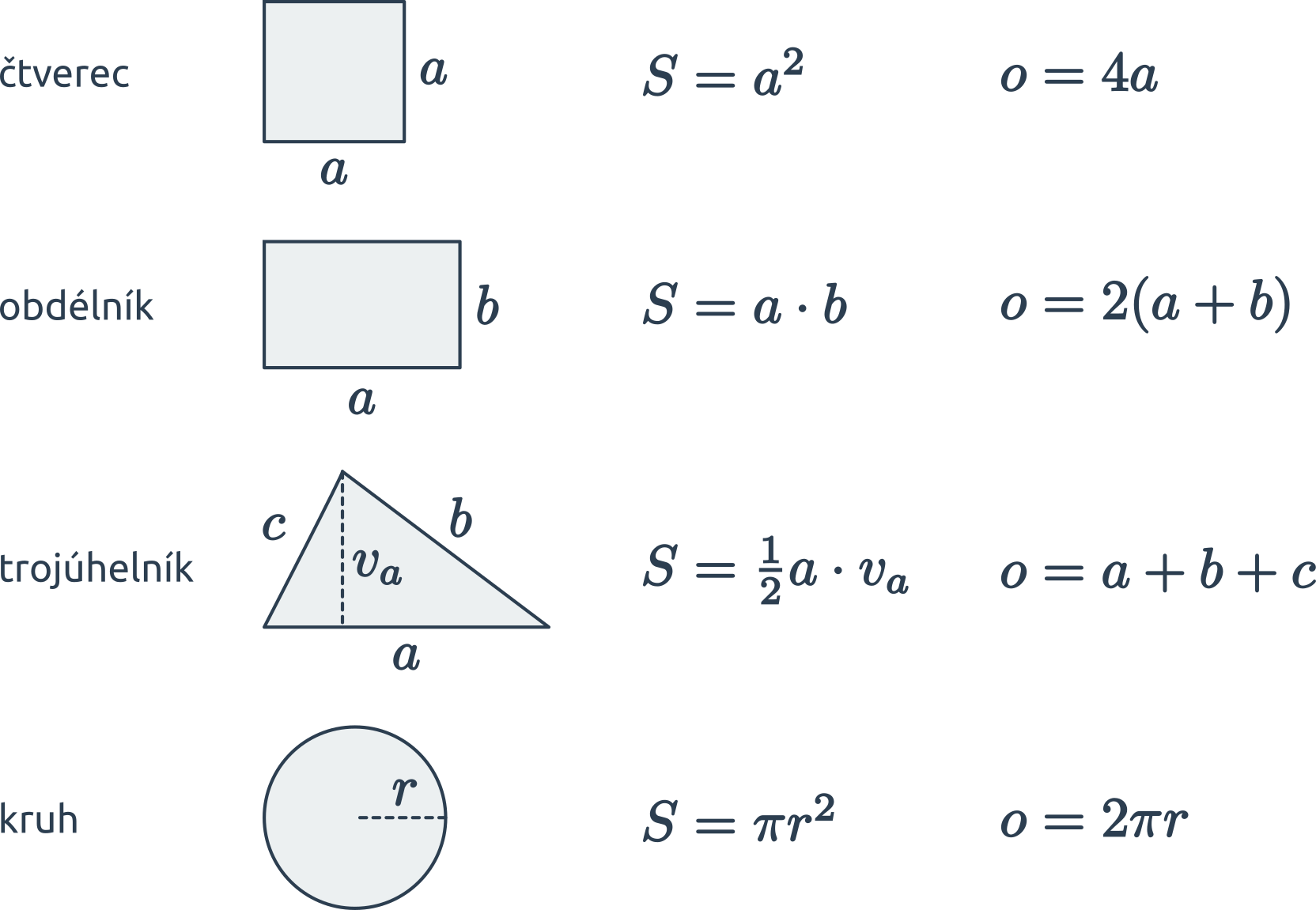
Přehled vzorců je dispozici také jako Obsah a obvod: pomůcka k vytištění.
NahoruObvod trojúhelníku
Obvod trojúhelníku spočítáme jako součet délek jeho stran: o=a+b+c
Příklad: obvod trojúhelníku
Trojúhelník na obrázku má délky stran a=10, b=8, c=14, takže jeho obvod je o=a+b+c=10+8+14=32.
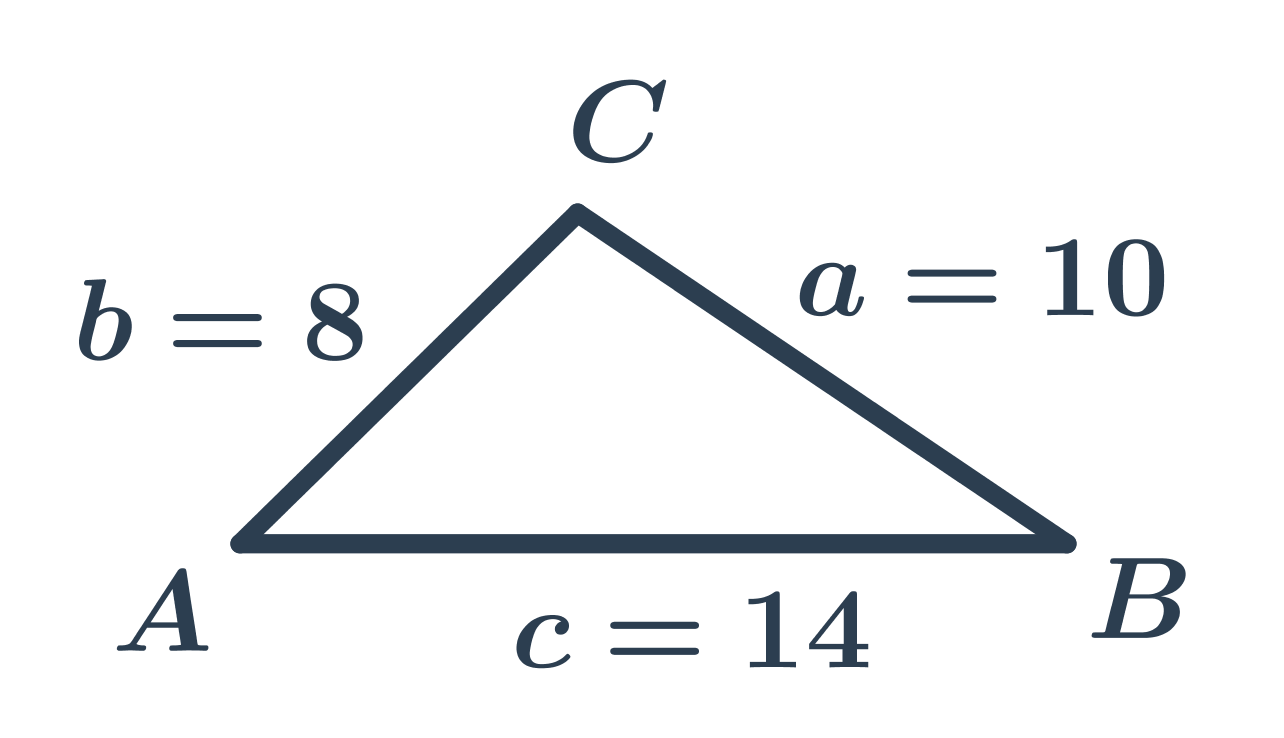
Obvod čtverce a obdélníku
Obvod čtverce o straně délky a je o=a+ a+a+a= 4a.
Obvod obdélníku se stranami o délkách a,b je roven o=a + b + a + b = 2\cdot (a+b).
NahoruObvod rovnoběžníku
Obvod rovnoběžníku se stranami o délkách a,b je roven S=a + b + a + b = 2\cdot (a+b).
NahoruObvod lichoběžníku
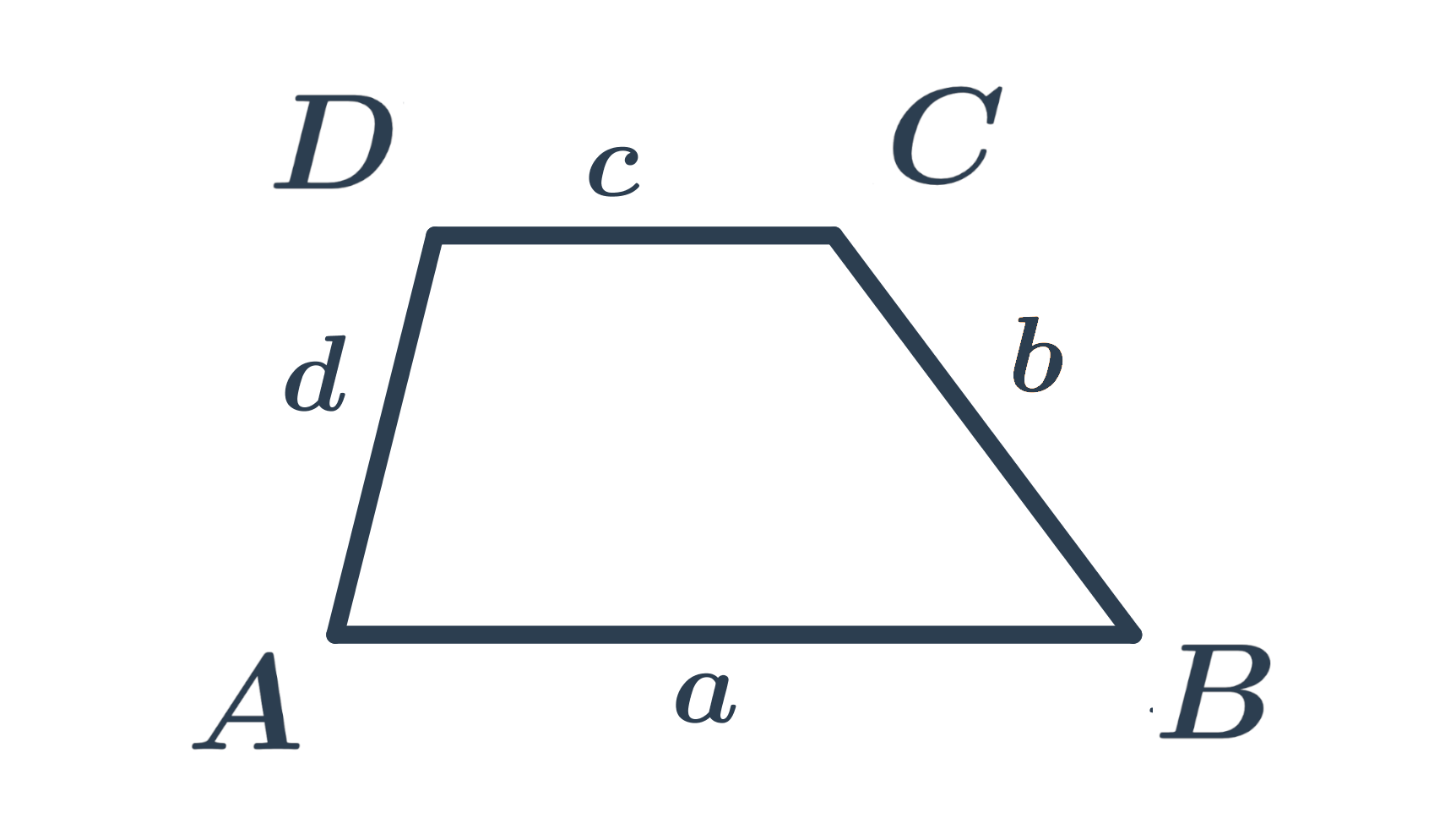
Obvod lichoběžníku je součet délek jeho stran. Tedy obvod lichoběžníku ABCD se stranami o délkách a,b,c,d vypočítáme podle vzorečku o=a+b+c+d.
Obvod kruhu, délka kružnice
Vzorec pro obvod kruhu
Obvod kruhu (i kružnice) o poloměru r je o=2\pi r. Pro průměr d platí o = \pi d.
Konstanta \pi se nazývá též Ludolfovo číslo. \pi je iracionální číslo, což znamená, že nejde vyjádřit zlomkem ani zapsat přesně v desítkové soustavě. Přibližná hodnota \pi je 3,141 592 65.
Při výpočtu obvodu kruhu dáváme dobrý pozor na to, zda vycházíme ze znalosti poloměru r nebo průměru d = 2r. Záměna průměru za poloměr je častou chybou.
Intuice
Základní intuici za vzorcem pro výpočet obvodu kruhu přibližuje níže uvedený obrázek. Obvod oranžového čtverce je 8\cdot r. Obvod kruhu je „o trochu menší“ – je to 2\pi \cdot r \approx 6{,}3 \cdot r.

Příklady: obvod kruhu
- Mějme kruh o poloměru 3 cm. Jeho obvod je 2\pi \cdot 3 \approx 2 \cdot 3{,}14 \cdot 3 \approx 18{,}8 cm.
- Kružnice o průměru 2 cm má délku \pi \cdot 2 \approx 6,3 cm.
- Středový kruh na fotbalovém hřišti má poloměr 9{,}1 metru. Pokud jej chceme obejít po jeho okrajové čáře, ujdeme 2 \pi \cdot 9{,}1 \approx 57 metrů.
Délka oblouku
Délku oblouku, který na kružnici o poloměru r odpovídá středovému úhlu \alpha spočítáme jako: \frac{\alpha}{360^{\circ}} \cdot 2 \pi \cdot r
Příklad – délka oblouku odpovídajícího 90^{\circ}
Délka oblouku na obrázku je:
\frac{90^{\circ}}{360^{\circ}} \cdot 2\pi \cdot 3 = \frac{1}{4} \cdot 6 \pi = \frac{3}{2}\pi
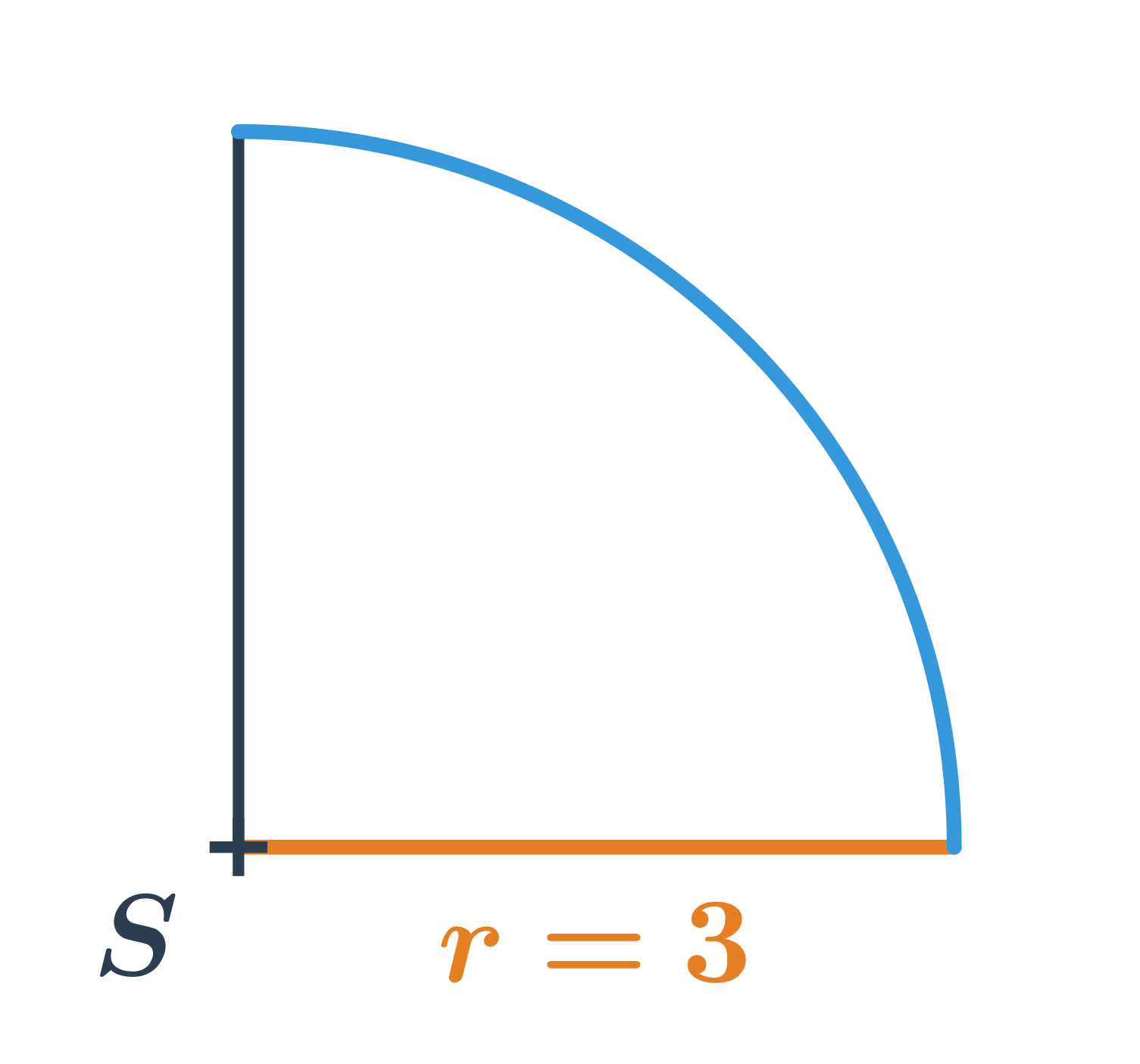 Jedná se o čtvrtinu délky kružnice.
Jedná se o čtvrtinu délky kružnice.
Příklad – délka oblouku odpovídajícího 360^{\circ}
Délka celé kružnice (tedy pro celých 360^{\circ}) je:
\frac{360^{\circ}}{360^{\circ}} \cdot 2\pi \cdot r = 2\pi \cdot r
Obvod: mix
Obvod u trojúhelníků a čtyřúhelníků je prostě součet délek jejich stran.
| Útvar | Vlastnosti | Obvod |
|---|---|---|
| trojúhelník | strany a, b, c | o = a + b + c |
| čtverec | strana a | o = 4a |
| obdélník | strany a, b | o = 2(a+b) |
| rovnoběžník | strany a, b | o = 2(a+b) |
| obecný čtyřúhelník | strany a, b, c, d | o = a+b+c+d |
Obsah trojúhelníku
Obsah trojúhelníku spočítáme jako součin délky libovolné strany trojúhelníka a výšky příslušné k této straně, takže: S_{\triangle} = \frac12 \cdot a \cdot v_a = \frac12 \cdot b \cdot v_b = \frac12 \cdot c \cdot v_c
Což si můžeme představit jako polovinu obsahu obdélníku, ve kterém je náš trojúhelník takto vepsán:
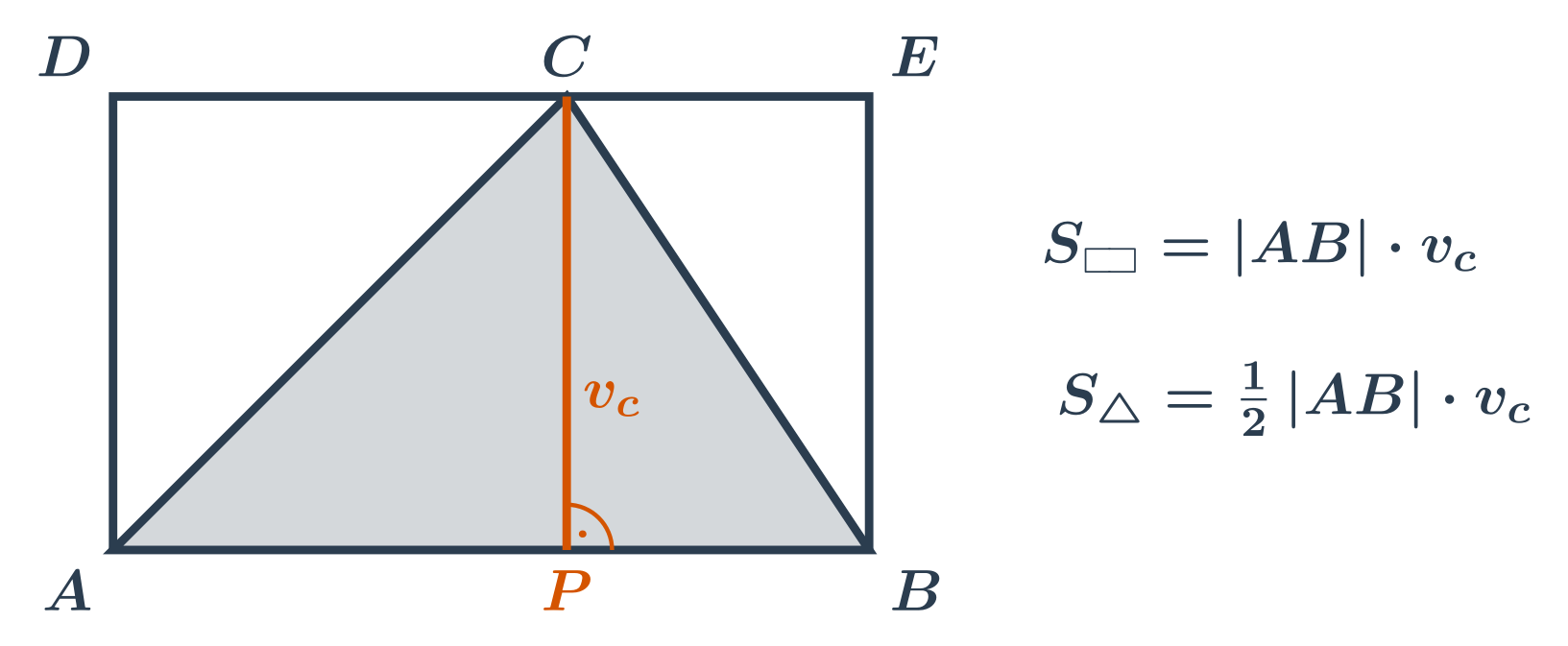
Příklady: obsah ostroúhlých trojúhelníků
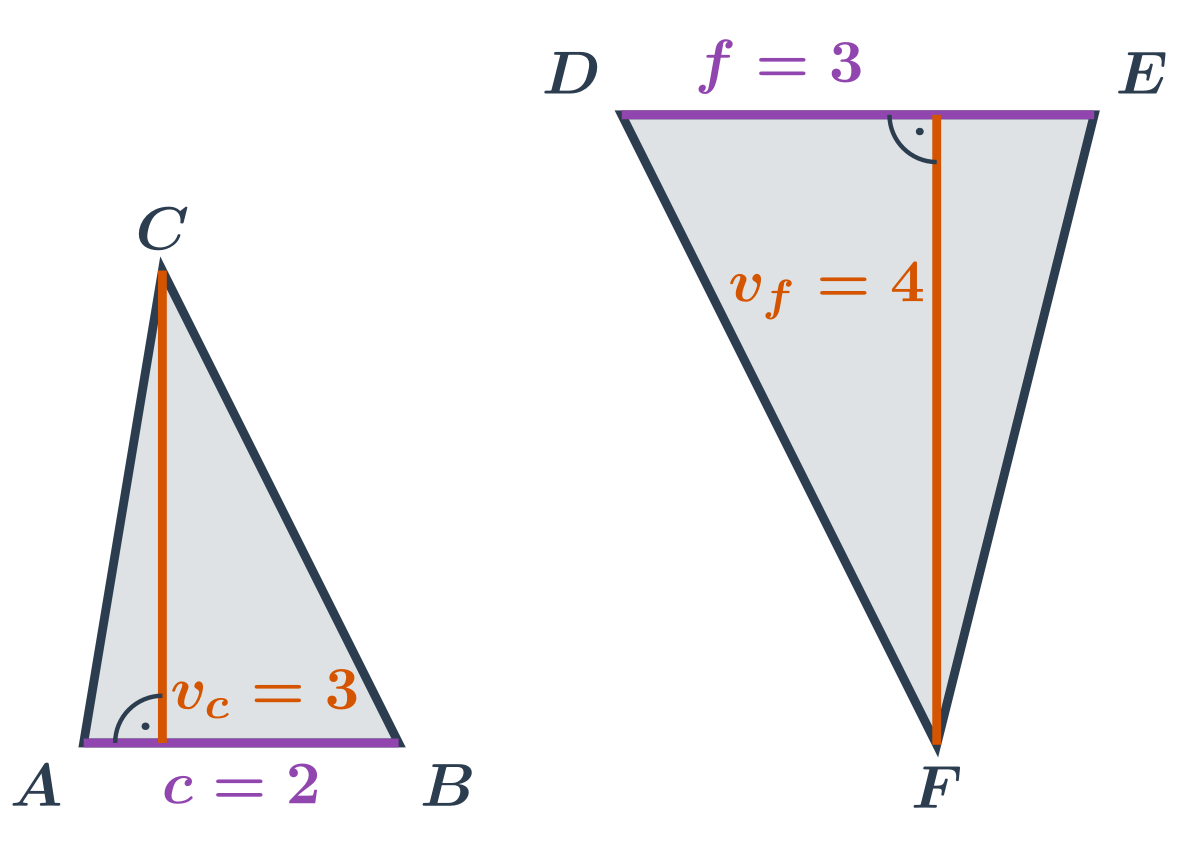
- Trojúhelník ABC: Délka strany \left| AB \right| je 2. Velikost k ní příslušné výšky v_c je 3. Obsah trojúhelníku ABC je roven \frac12 \cdot 2 \cdot 3 = 3.
- Trojúhelník DEF: Nevadí nám, že trojúhelník na náčrtku vypadá zvláštně natočený. Známe délku strany \left| DE \right|, což je 3. Velikost k ní příslušné výšky v_f je 4. Obsah trojúhelníku DEF je roven \frac12 \cdot 3 \cdot 4 = 6.
Příklady: obsah tupoúhlého a pravoúhlého trojúhelníku
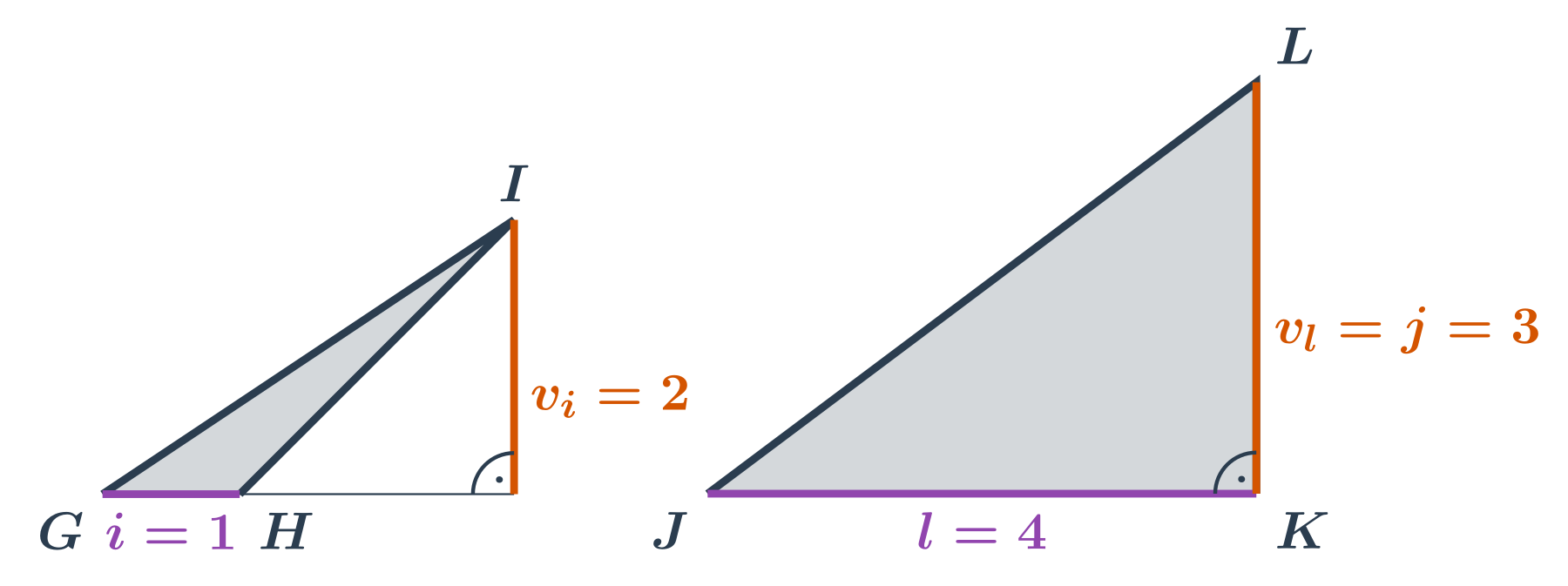
- Trojúhelník GHI: Nevadí nám ani když je pata kolmice, na které leží výška, mimo stranu trojúhelníka. Délka strany \left| GH \right| je 1. Velikost k ní příslušné výšky v_i je 2. Obsah trojúhelníku GHI je \frac12 \cdot 2 \cdot 1 = 1.
- Trojúhelník JKL: S pravoúhlým trojúhelníkem si také poradíme. Délka strany \left| JK \right| je 4. Velikost k ní příslušné výšky v_l je 3 (a je to zároveň i délka strany KL našeho trojúhelníku). Obsah trojúhelníku JKL je \frac12 \cdot 4 \cdot 3 = 6.
Obsah čtverce a obdélníku
Obsah čtverce o straně délky a je S=a\cdot a=a^2.
Obsah obdélníku se stranami o délkách a,b je roven S=a\cdot b.
NahoruObsah rovnoběžníku
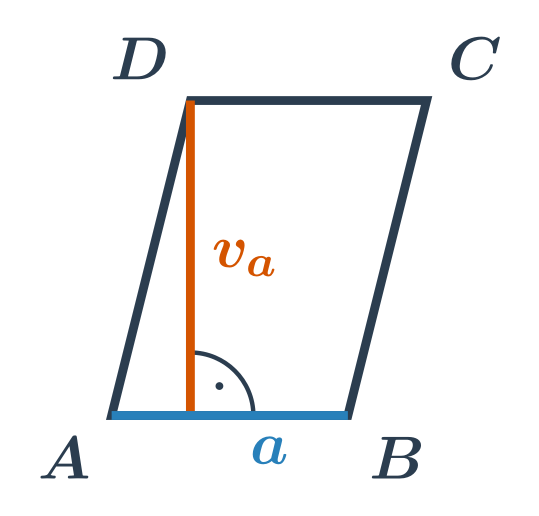
Obsah rovnoběžníku je roven součinu délky strany a k ní příslušné výšky. Tedy obsah rovnoběžníku ABCD, ve kterém ke straně o délce a přísluší výška v_a spočítáme jako S= a\cdot v_a.
Obsah lichoběžníku
Obsah lichoběžníku se základnami o délkách a,c a výškou v spočítáme podle vzorečku S=\frac{1}{2} \cdot (a+c) \cdot v.
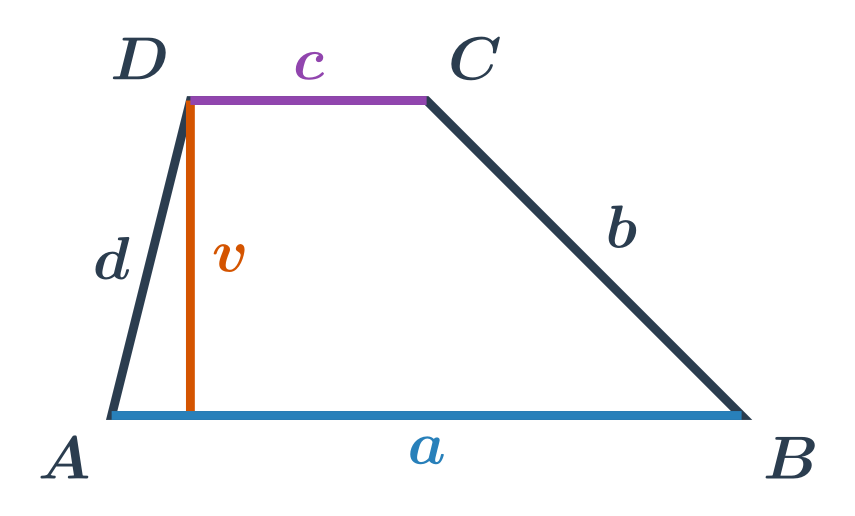
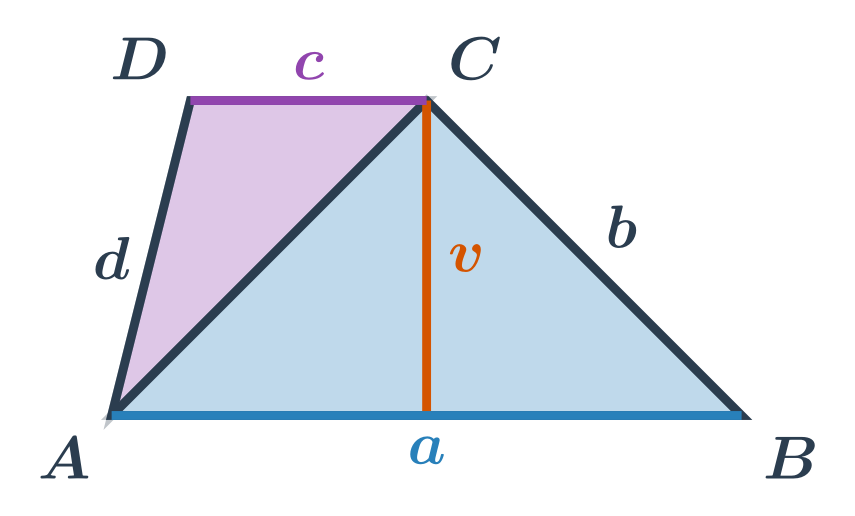
Intuice za tímto vzorečkem je vidět na následujícím obrázku. Obsah lichoběžníku je roven součtu obsahů dvou trojúhelníků.
- První trojúhelník má výšku v příslušnou ke straně délky a. Jeho obsah je S_{ABC}=\frac{1}{2} \cdot a \cdot v.
- Druhý trojúhelník má výšku v příslušnou ke straně délky c. Jeho obsah je S_{ACD}=\frac{1}{2} \cdot c \cdot v.
Součet obsahů těchto dvou trojúhelníků je S = S_{ABC} + S_{ACD} = \frac{1}{2} \cdot a \cdot v + \frac{1}{2} \cdot c \cdot v = \frac{1}{2} \cdot (a+c) \cdot v
Obsah kruhu
Vzorec pro obsah kruhu
Obsah kruhu o poloměru r je S=\pi r^2. Pro průměr d platí S = \frac{1}{4} \pi d^2.
Konstanta \pi se nazývá též Ludolfovo číslo. \pi je iracionální číslo, což znamená, že nejde vyjádřit zlomkem ani zapsat přesně v desítkové soustavě. Přibližná hodnota \pi je 3,141 592 65.
Při výpočtu obsahu kruhu dáváme dobrý pozor na to, zda vycházíme ze znalosti poloměru nebo průměru. Záměna průměru za poloměr je častou chybou.
Intuice
Základní intuici za vzorcem pro výpočet obsahu kruhu přibližuje níže uvedený obrázek. Žluté čtverce mají obsah r^2. Oranžový čtverec se skládá ze čtyř žlutých čtverců, takže má obsah 4\cdot r^2. Kruh má „o trochu menší“ obsah než oranžový čtverec, což odpovídá tomu, že obsah kruhu je přibližně 3{,}14 \cdot r^2.

Příklady
- Mějme kruh o poloměru 3 cm. Jeho obsah je \pi \cdot 3^2 \approx 3{,}14\cdot 9 \approx 28,3 cm².
- Uvažujme kružnici o průměru 2 cm. Její vnitřní oblast má obsah \frac{1}{4} \pi \cdot 2^2 = \pi \approx 3,14 cm².
- Středový kruh na fotbalovém hřišti má poloměr 9{,}1 metru. Pokud bychom chtěli veškerou trávu v kruhu nabarvit na růžovo, museli bychom nabarvit \pi \cdot 9{,}1^2 \approx 260 m² trávy.
Komiks pro zpestření
Obsah kruhové výseče
Obsah kruhové výseče
Obsah kruhové výseče se středovým úhlem \alpha a poloměrem r spočítáme jako: \frac{\alpha}{360^{\circ}} \cdot \pi \cdot r^2
Příklady
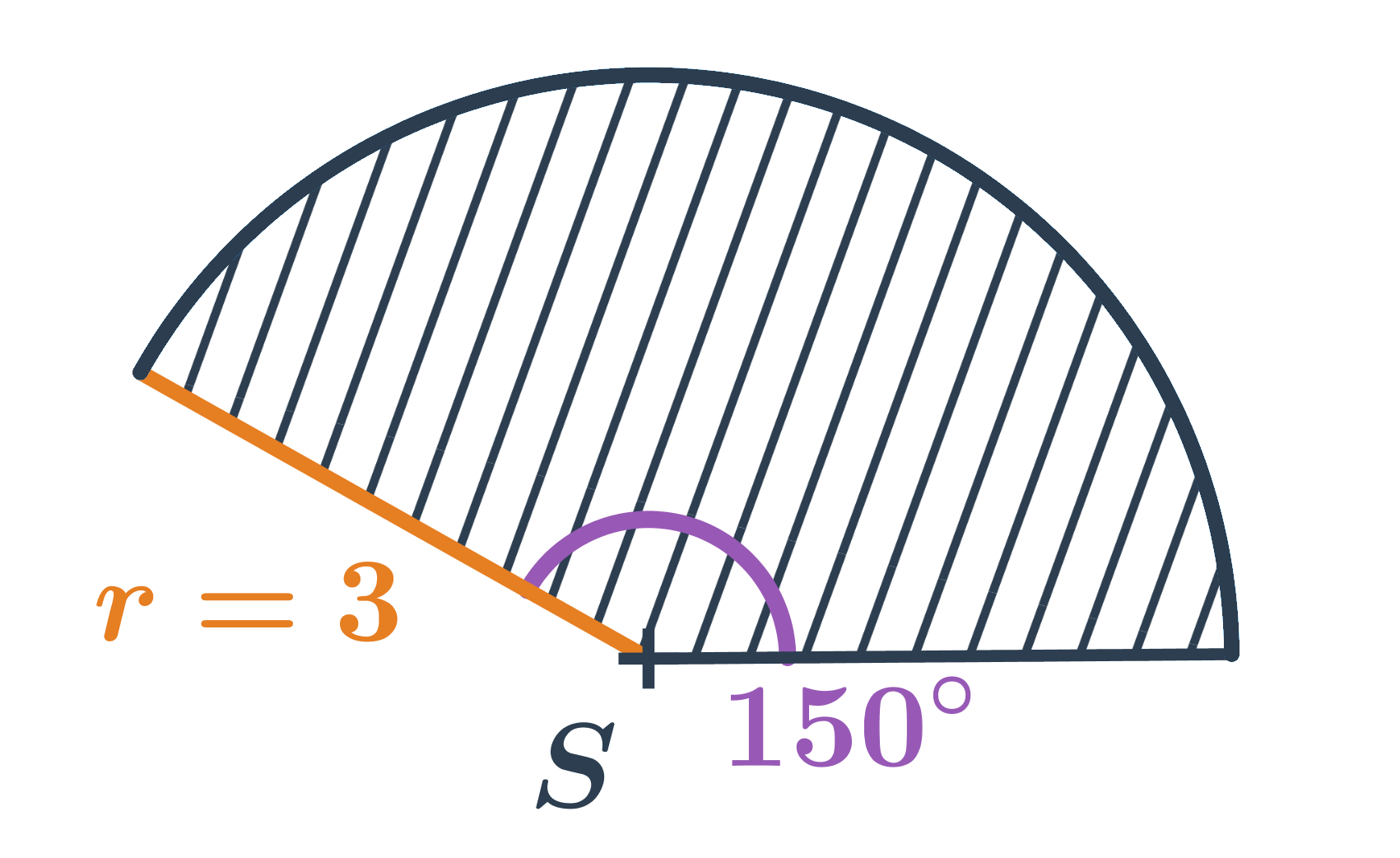
- Kruhová výseč na obrázku má obsah: \frac{150^{\circ}}{360^{\circ}} \cdot \pi \cdot 3^2 = \frac{5}{12} \cdot \pi \cdot 9 = \frac{15}{4} \pi
- Obsah celého kruhu (výseče se středovým úhlem 360^{\circ}) je: \frac{360^{\circ}}{360^{\circ}} \cdot \pi \cdot r^2 = \pi \cdot r^2

