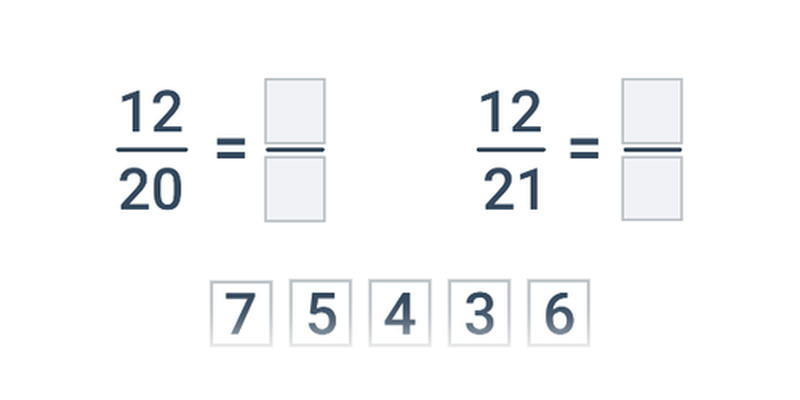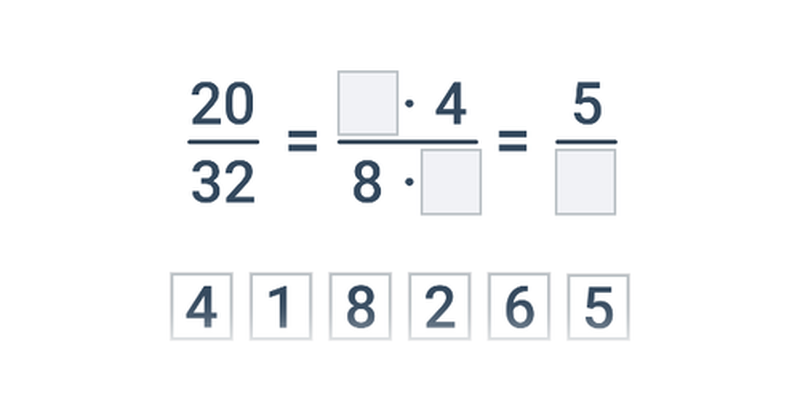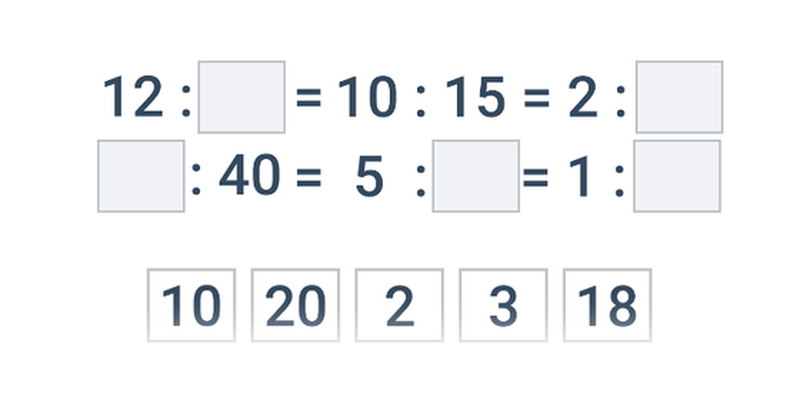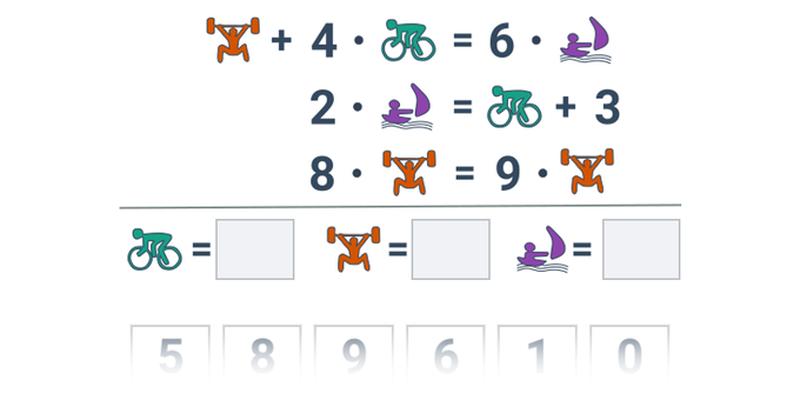Příprava na přijímací zkoušky na šestiletá gymnázia, matematika
Zpět na rozcestník k přípravě na přijímací zkoušky
Procvičování v Umíme doporučujeme kombinovat s řešením testových zadání z předchozích let. Zadání v Umíme jsou vhodná především pro přípravu a učení, testová zadání pak pro seznámení s formální podobou testů.
Uvedený výběr témat k procvičování pokrývá všechny oblasti uvedené v oficiální specifikaci požadavků k jednotné přijímací zkoušce. Systém Umíme nabízí velmi bohaté možnosti procvičování a uvedený výběr zdaleka nezmiňuje všechny dostupné možnosti. Tato stránka uvádí pouze výběr cvičení, která jsou nejvíce užitečná pro přípravu na přijímací zkoušky. Při výběru bylo zohledněno mimo jiné i to, jaké úlohy byly používané v přijímacích zkouškách v minulých letech.
Pokud budete potřebovat k některému tématu důkladnější procvičení, můžete najít další cvičení skrze vyhledávání názvu tématu. Systém vám bude také automaticky doporučovat další návaznosti. Lze také použít kompletní výpis témat pro 7. ročník.
Následující tabulka uvádí časový odhad při pravidelném procvičování 15 minut denně.
| Varianta procvičování | Rozsah výpisu | Komentář | Časový rozsah procvičování |
|---|---|---|---|
| Základní | 69 sad | Základní procvičování, které má smysl si určitě projít pro osvěžení všech témat, která se ve zkouškách vyskytují. | měsíc |
| S rozcvičením | 90 sad | Základní procvičování rozšířené o přípravná cvičení zaměřená na témata, která často dělají problémy. | 2–3 měsíce |
| S bonusem | 96 sad | Základní procvičení rozšířené o náročnější cvičení, která pomohou s průpravou i na náročnější příklady ze zkoušek. | 2–3 měsíce |
| Důkladné | 117 sad | Kombinace předchozího, tj. od přípravných cvičení až po bonusy. | 3 a více měsíců |
- Dělitelnost
- Zlomky a desetinná čísla
- Procenta
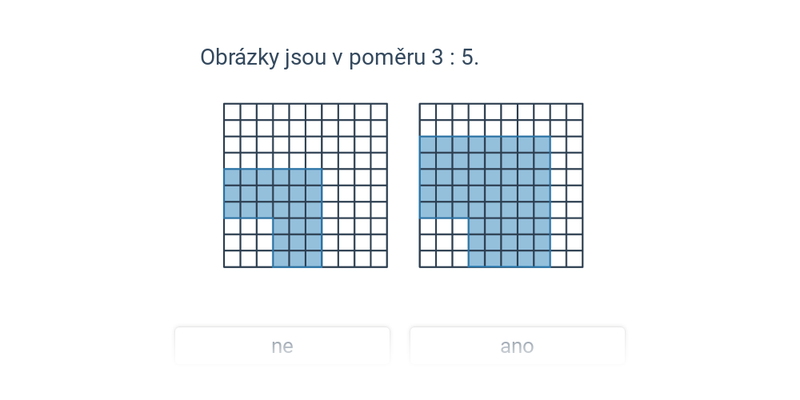
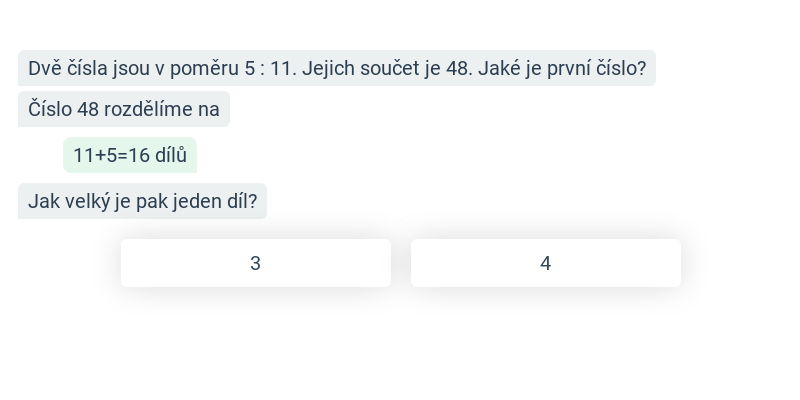
- Poměry, přímá a nepřímá úměra
- Geometrie: pojmy, útvary
- Osová a středová souměrnost
- Obsah, obvod, objem, povrch
- Úhly
- Konstrukční úlohy
- Nestandardní úlohy
1. Dělitelnost
Důkladné zvládnutí dělitelnosti je důležité, protože se využívá i v dalších tématech (zlomky, poměry).
| Rozhodovačka | Podmínky dělitelnosti | ||
| Rozhodovačka | Prvočísla | ||
| Krok po kroku | NSD bez použití mocnin | ||
| Pexeso | Největší společný dělitel | ||
| Psaná odpověď | Největší společný dělitel | ||
| Krok po kroku | NSN bez použití mocnin | ||
| Pexeso | Nejmenší společný násobek | ||
| Psaná odpověď | Nejmenší společný násobek | ||
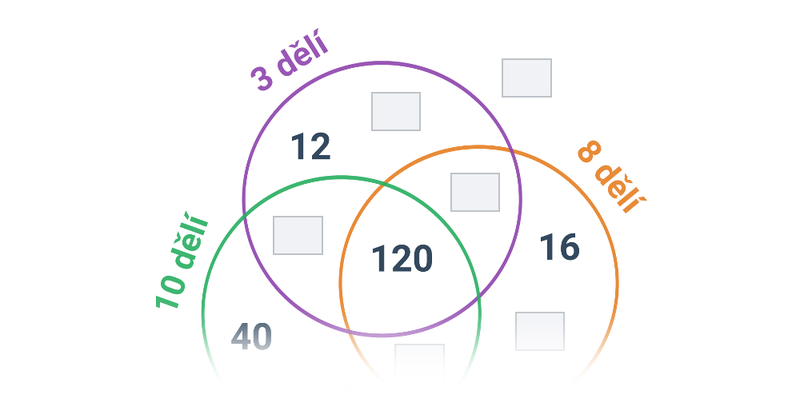
| Přesouvání | Dělitelnost a Vennův diagram | ||
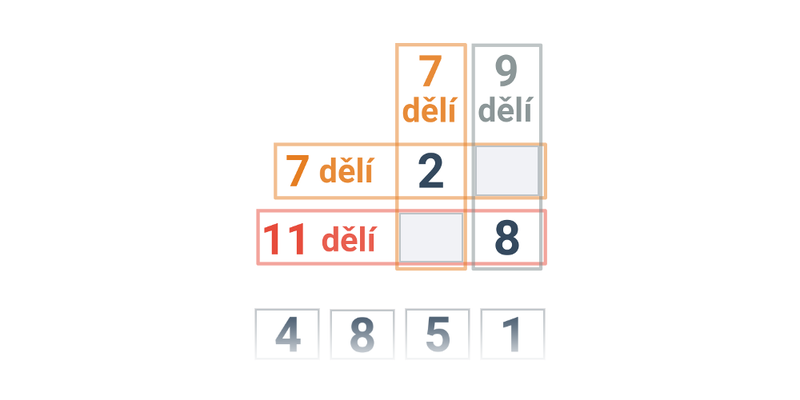
| Přesouvání | Křížovka dělitelnosti |
2. Zlomky a desetinná čísla
Použití zlomků a desetinných čísel se může vyskytovat v samostatných úlohách i jako součást větších příkladů (např. slovních úloh).
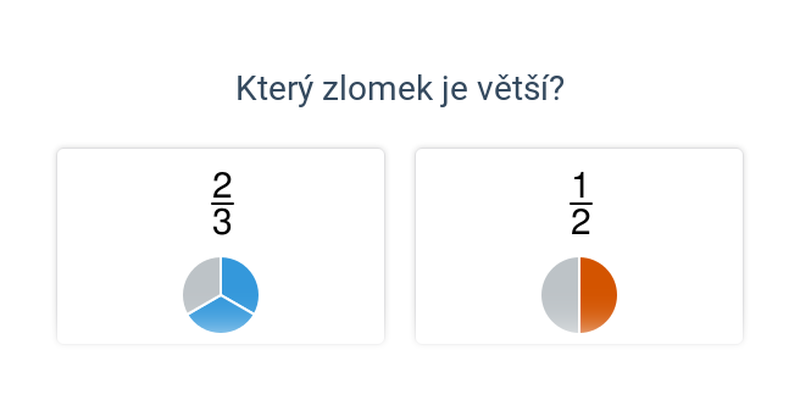
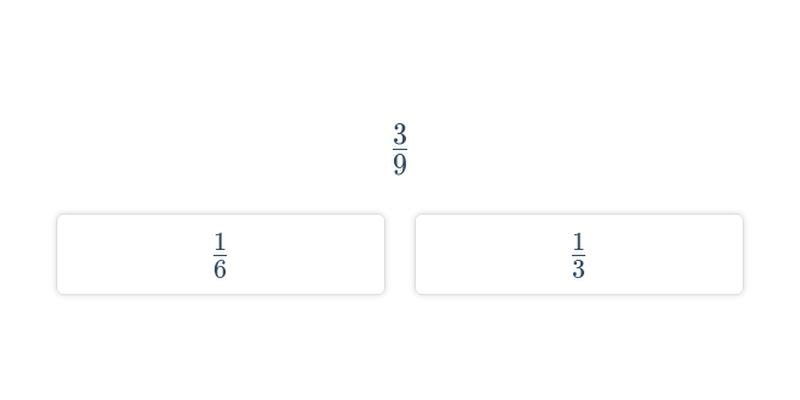
| Rozhodovačka | Porovnávání zlomků | ||
| Rozhodovačka | Porovnávání zlomků | ||
| Přesouvání | Porovnávání zlomků | ||
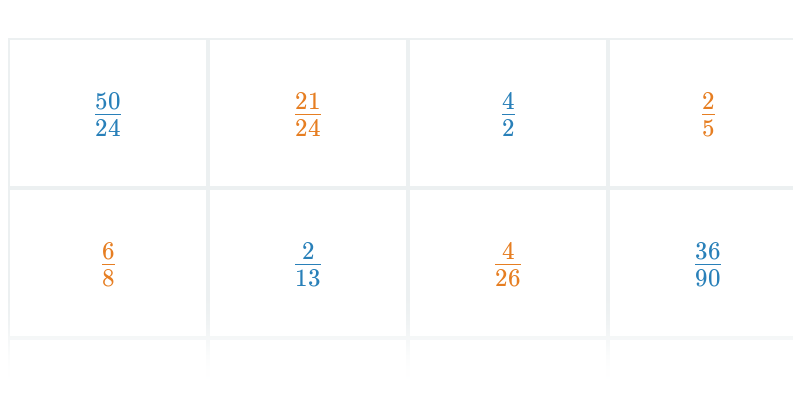
| Přesouvání | Krácení zlomků | ||
| Přesouvání | Krácení zlomků | ||
| Rozhodovačka | Krácení zlomků | ||
| Pexeso | Krácení zlomků | ||
| Pexeso | Smíšená čísla | ||
| Psaná odpověď | Smíšená čísla | ||
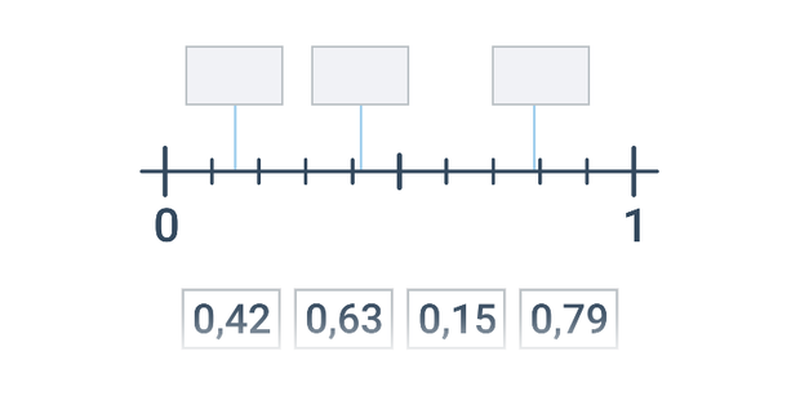
| Přesouvání | Zlomky na číselné ose | ||
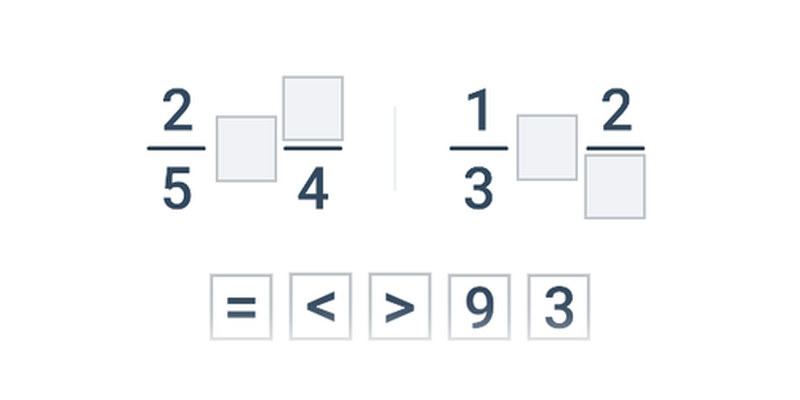
| Rozhodovačka | Porovnávání zlomků | ||
| Krok po kroku | Kombinace operací se zlomky | ||
| Psaná odpověď | Kombinace operací se zlomky | ||
| Psaná odpověď | Výpočty se zlomky: mix | ||
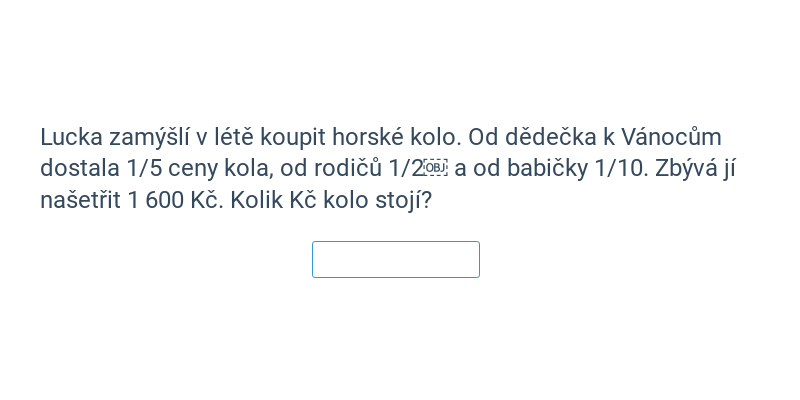
| Slovní úlohy | Výpočty se zlomky: mix | ||
| Slovní úlohy | Výpočty se zlomky: mix | ||
| Slovní úlohy | Výpočty se zlomky: mix | ||
| Přesouvání | Zlomky a desetinná čísla | ||
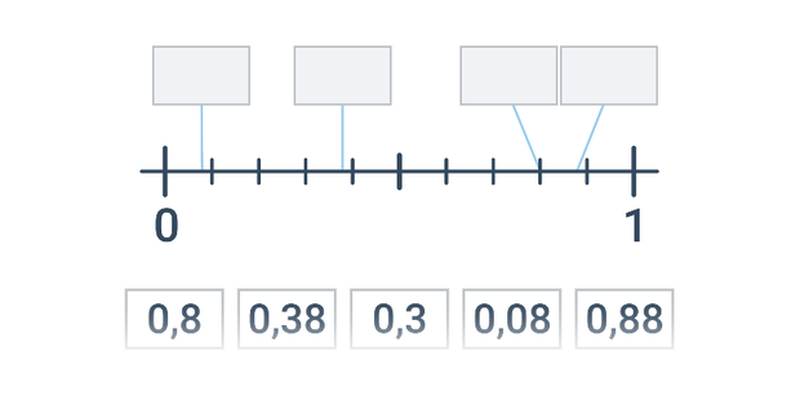
| Přesouvání | Desetinná čísla na číselné ose | ||
| Přesouvání | Desetinná čísla na číselné ose | ||
| Psaná odpověď | Sčítání a odčítání desetinných čísel | ||
| Psaná odpověď | Sčítání a odčítání desetinných čísel | ||
| Rozhodovačka | Výpočty s desetinnými čísly: mix | ||
| Slovní úlohy | Výpočty s desetinnými čísly: mix |
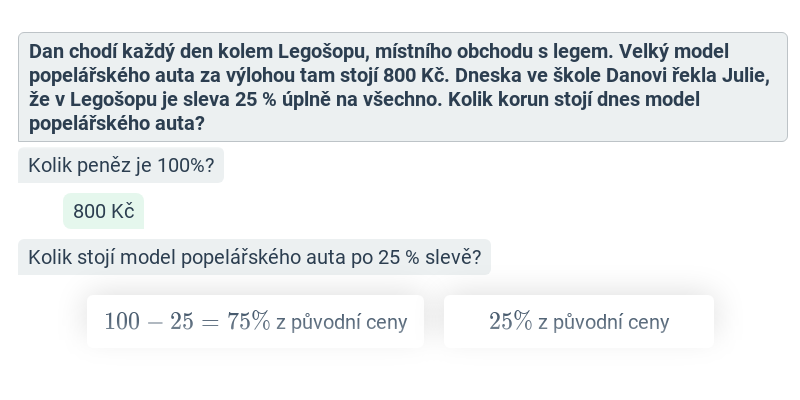
3. Procenta
Procenta se často vyskytují v rámci slovních úloh. Přirozeně se využívají například u úloh s finanční tematikou, což je také jedno z témat vyskytujících se ve zkouškách.
| Přesouvání | Procenta: poznávání | ||
| Přesouvání | Procenta: poznávání | ||
| Rozhodovačka | Odhady procent – tečky | ||
| Pexeso | Počítání s procenty | ||
| Pexeso | Zlomky a procenta | ||
| Rozhodovačka | Přibližné počítání s procenty | ||
| Krok po kroku | Počítání s procenty | ||
| Psaná odpověď | Počítání s procenty | ||
| Slovní úlohy | Procenta: mix | ||
| Slovní úlohy | Procenta: mix | ||
| Slovní úlohy | Procenta: mix |
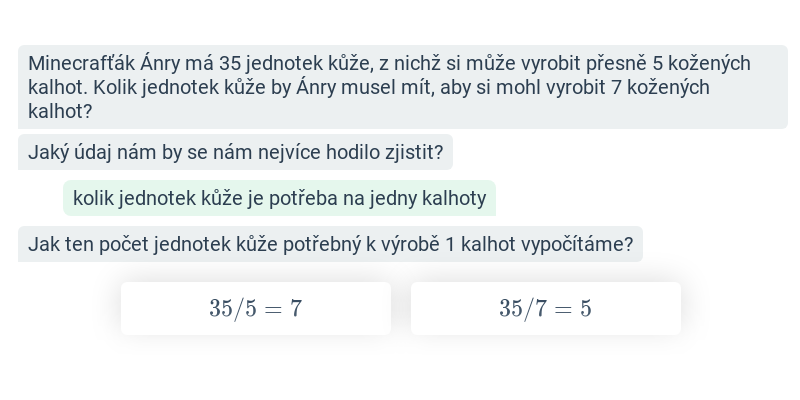
4. Poměry, přímá a nepřímá úměra
Poměry a úměrnosti patří mezi typická témata u zkoušek na šestiletá gymnázia, používají se v samostatných příkladech i v úlohách na práci s daty.
| Rozhodovačka | Trojčlenka | ||
| Rozhodovačka | Přímá a nepřímá úměrnost | ||
| Krok po kroku | Přímá a nepřímá úměrnost | ||
| Slovní úlohy | Přímá a nepřímá úměrnost | ||
| Přesouvání | Poměry: základy | ||
| Rozhodovačka | Poměry: změna a rozdělení čísla | ||
| Krok po kroku | Poměry: výpočty | ||
| Psaná odpověď | Poměry: výpočty | ||
| Rozhodovačka | Poměry: výpočty | ||
| Psaná odpověď | Poměry: změna a rozdělení čísla | ||
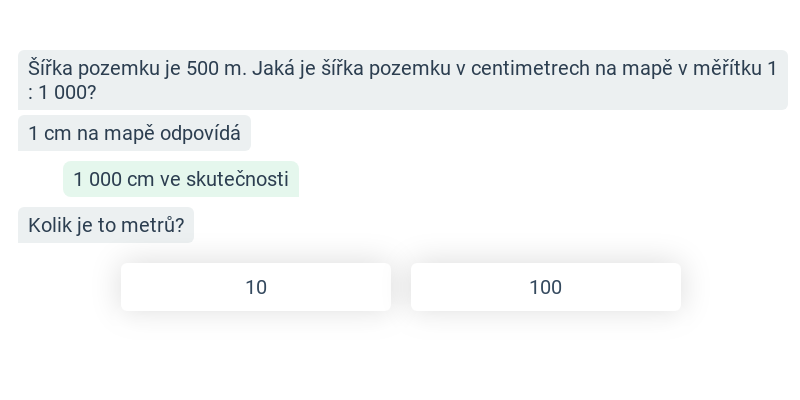
| Krok po kroku | Poměry: měřítko mapy | ||
| Psaná odpověď | Poměry: měřítko mapy | ||
| Slovní úlohy | Poměry: výpočty |
5. Geometrie: pojmy, útvary
Další skupina témat se týká geometrie. Základem je znalost jednotlivých útvarů a souvisejících pojmů.
| Rozhodovačka | Názvy geometrických útvarů a těles | ||
| Pexeso | Názvy geometrických útvarů a těles | ||
| Rozhodovačka | Pojmy související s trojúhelníkem | ||
| Rozhodovačka | Pojmy: velikost úhlů | ||
| Rozhodovačka | Pojmy: dvojice úhlů | ||
| Přesouvání | Geometrické pojmy: mix | ||
| Pexeso | Geometrické pojmy: mix |
6. Osová a středová souměrnost
Osovou a středovou souměrnost je dobré nepodcenit. Základní princip je jednoduchý, ale člověk se u těchto operací snadno splete a je dobré si o nich vytvořit opravdu dobrou představu.
| Přesouvání | Osová souměrnost | ||
| Přesouvání | Osová souměrnost | ||
| Přesouvání | Středová souměrnost | ||
| Mřížkovaná | Osová souměrnost | ||
| Mřížkovaná | Osová souměrnost těžší | ||
| Mřížkovaná | Středová souměrnost | ||
| Mřížkovaná | Středová souměrnost těžší |
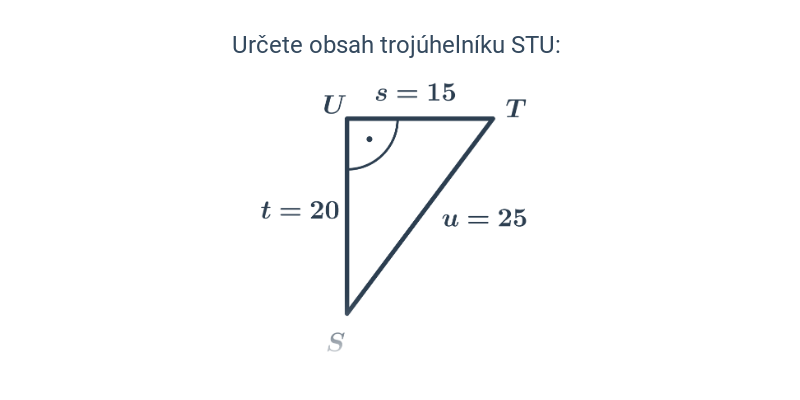
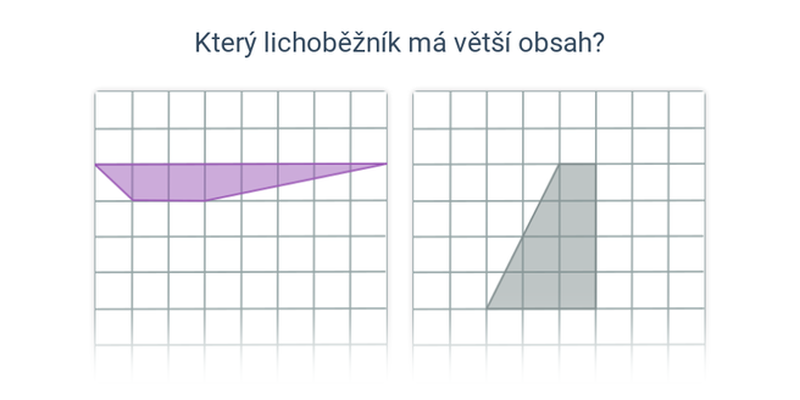
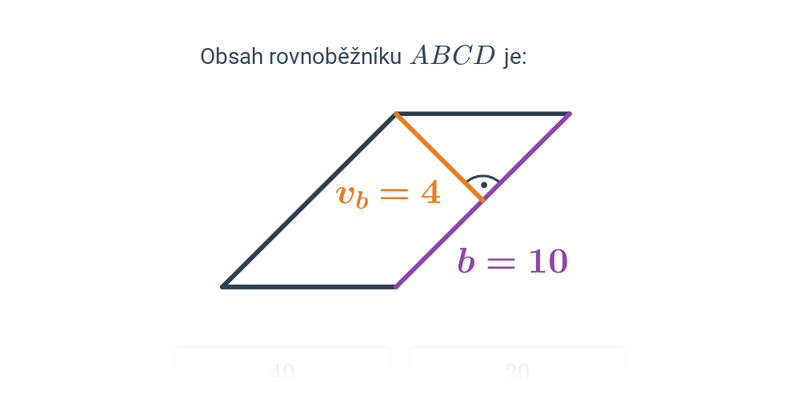
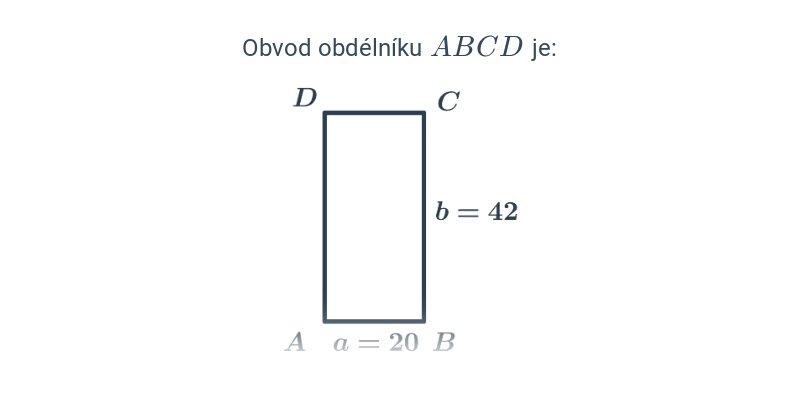
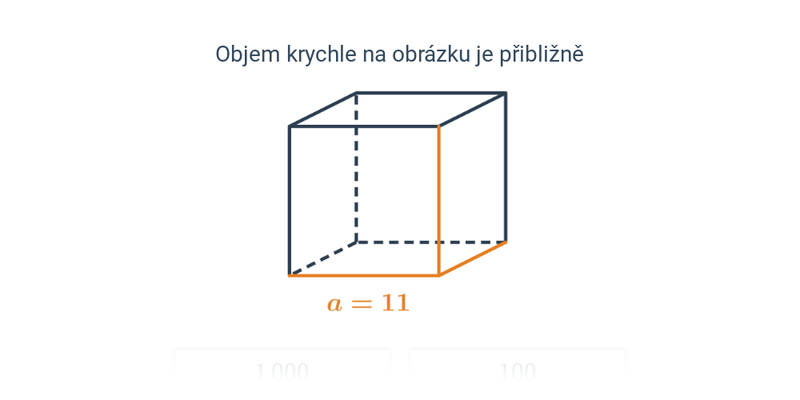
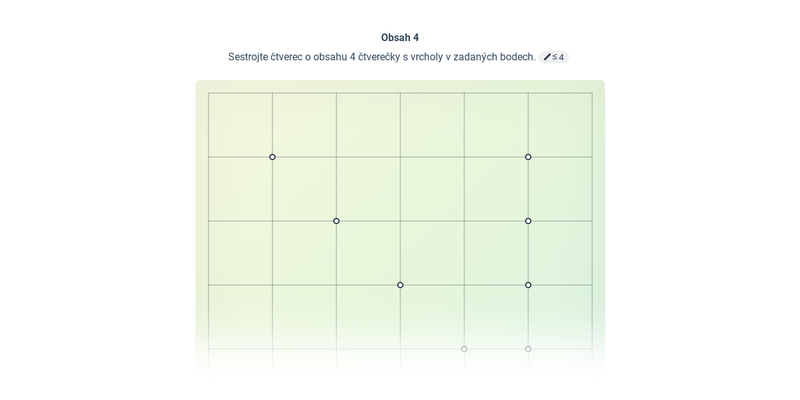
7. Obsah, obvod, objem, povrch
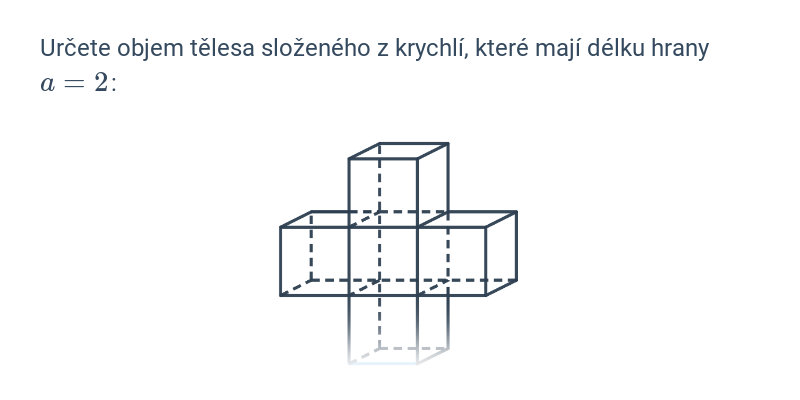
Mezi typické zkouškové úlohy patří výpočty obvodu a obsahu. Z prostorových útvarů je potřeba zvládnout objem a povrch krychle a kvádru.
| Přesouvání | Jednotky obsahu | ||
| Psaná odpověď | Jednotky obsahu | ||
| Přesouvání | Obsah na mřížce: mix | ||
| Psaná odpověď | Obvod trojúhelníku | ||
| Psaná odpověď | Obsah trojúhelníku | ||
| Rozhodovačka | Obsah na mřížce: trojúhelník, rovnoběžník, lichoběžník | ||
| Psaná odpověď | Obsah na mřížce: trojúhelník, rovnoběžník, lichoběžník | ||
| Rozhodovačka | Obsah lichoběžníku (na mřížce) | ||
| Rozhodovačka | Obsah: trojúhelník, rovnoběžník, lichoběžník | ||
| Psaná odpověď | Obvod: čtverec, obdélník, trojúhelník | ||
| Psaná odpověď | Obsah: trojúhelník, rovnoběžník, lichoběžník | ||
| Slovní úlohy | Obsah, obvod: mix | ||
| Rozhodovačka | Objem krychle a kvádru | ||
| Psaná odpověď | Objem krychle a kvádru | ||
| Psaná odpověď | Objem krychle a kvádru | ||
| Mřížkovaná | Obsah |
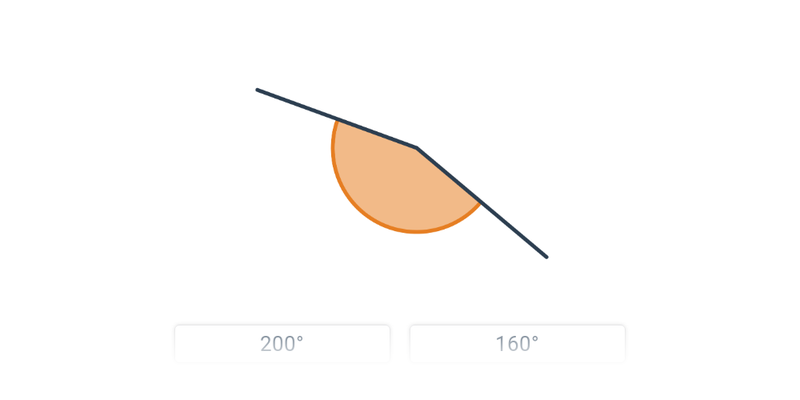
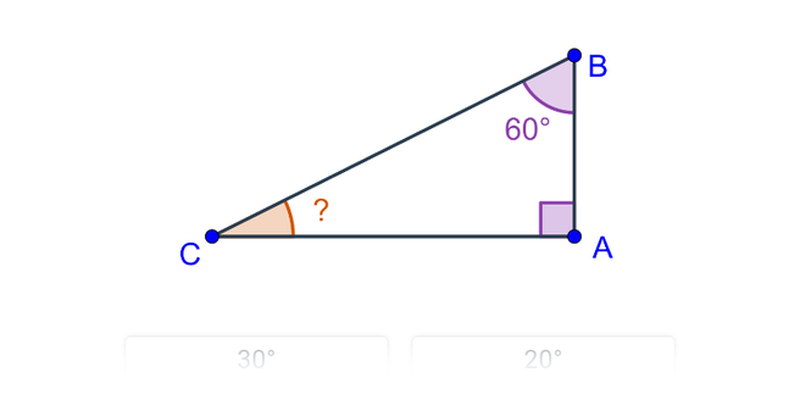
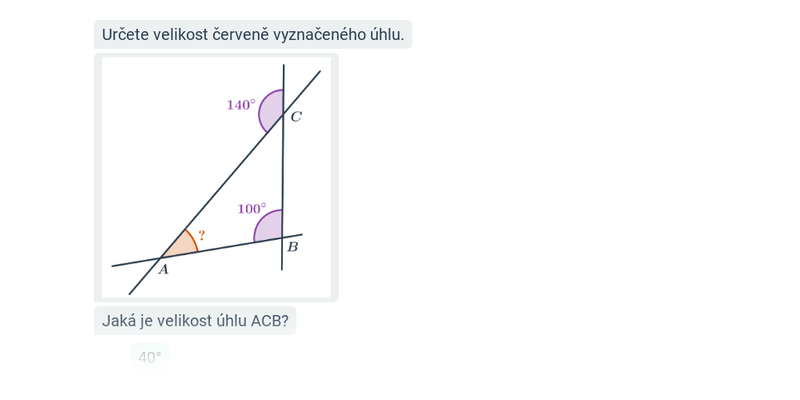
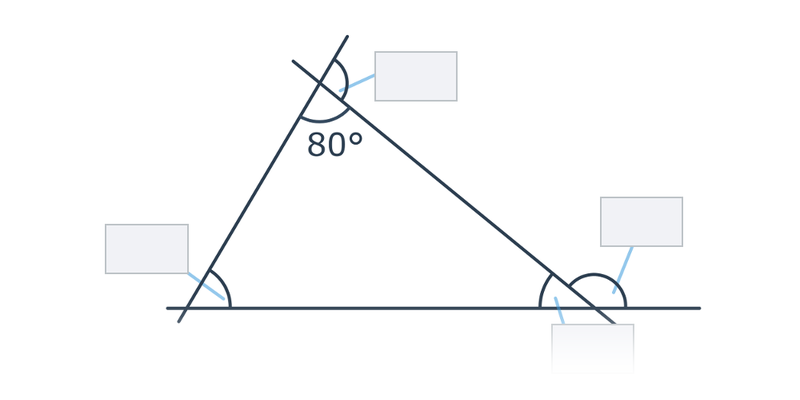
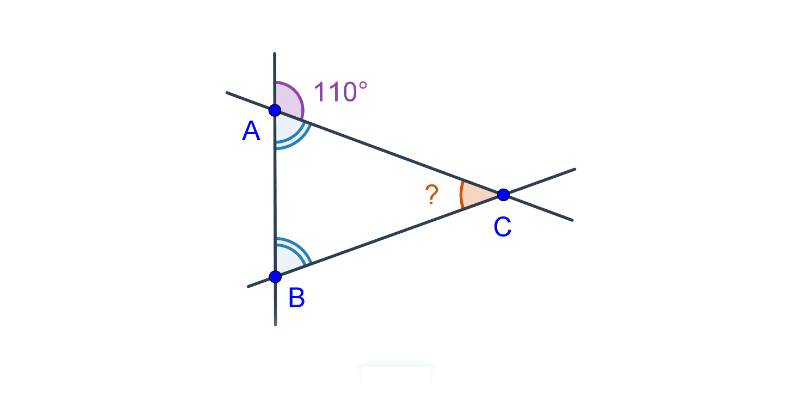
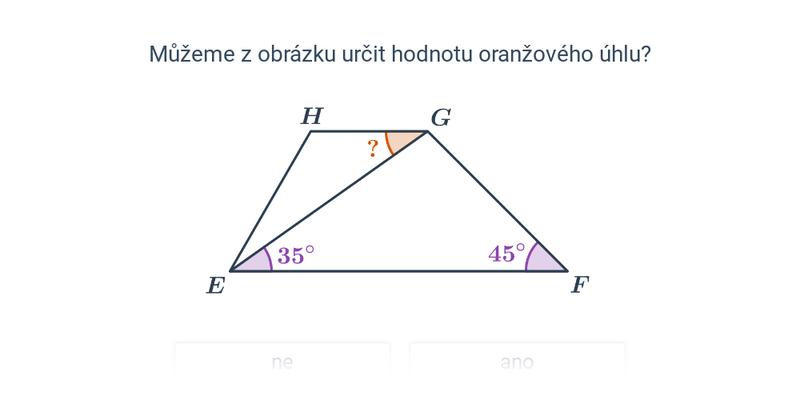
8. Úhly
Práce s úhly se vyskytuje jako dílčí krok v mnoha geometrikých úlohách (např. v konstrukčních).
| Rozhodovačka | Poznávání úhlů | ||
| Rozhodovačka | Úhly v trojúhelníku | ||
| Krok po kroku | Úhly v trojúhelníku | ||
| Přesouvání | Úhly v trojúhelníku | ||
| Psaná odpověď | Úhly v trojúhelníku | ||
| Rozhodovačka | Úhly ve čtyřúhelníku | ||
| Psaná odpověď | Úhly ve čtyřúhelníku | ||
| Psaná odpověď | Úhly: mix | ||
| Slovní úlohy | Slovní úlohy s úhly |
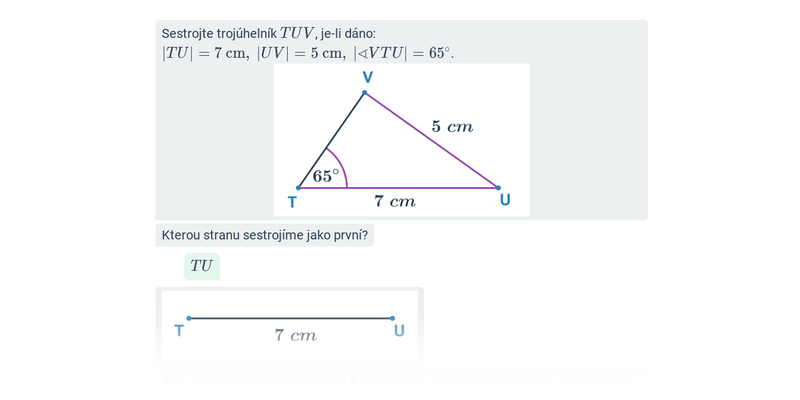
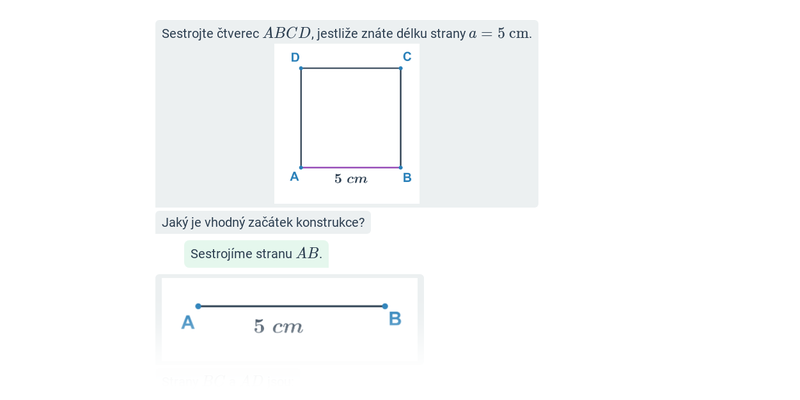
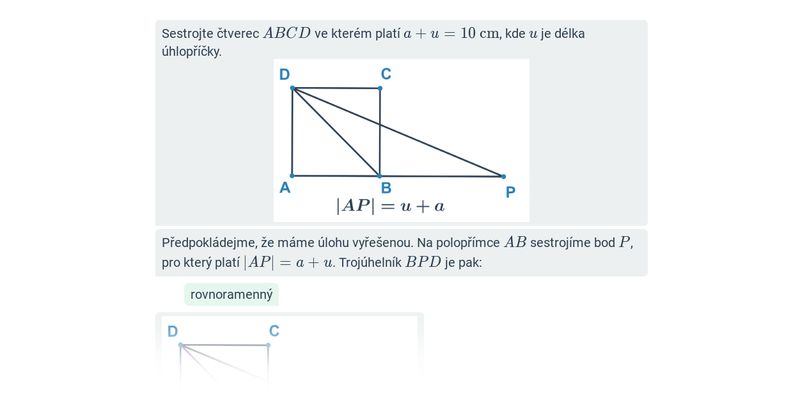
9. Konstrukční úlohy
Před samotným rýsováním se ale vyplatí projít si pojmy a postupy ve cvičeních na počítači. Konstrukční úlohy je pak potřeba trénovat i na papíře, k tomu lze využít například tyto pracovní listy: Konstrukce rovnostraných a rovnoramenných trojúhelníků (+ řešení), Konstrukce trojúhelníků podle vět (+ řešení).
| Mřížkovaná | Trojúhelníky | ||
| Mřížkovaná | Čtyřúhelníky | ||
| Krok po kroku | Konstrukce trojúhelníků: rovnoramenné a rovnostranné trojúhelníky | ||
| Krok po kroku | Konstrukce trojúhelníků: věty sss, sus, usu, Ssu | ||
| Krok po kroku | Konstrukce trojúhelníků: těžnice, výšky, vepsaná a opsaná kružnice | ||
| Krok po kroku | Konstrukce čtyřúhelníků: mix | ||
| Krok po kroku | Konstrukční úlohy průřezově |
10. Nestandardní úlohy
Součástí specifikace zkoušek jsou i „nestandardní aplikační úlohy“, které nelze řešit naučeným postupem a vyžadují použití úsudku a (prostorové) představivosti. Tento typ úloh samozřejmě nelze nadrilovat. V Umíme máme ale řadu pestrých úloh, které fungují jako dobrá příprava.
| Psaná odpověď | Počítání s nápadem | ||
| Přesouvání | Obrázkové rovnice | ||
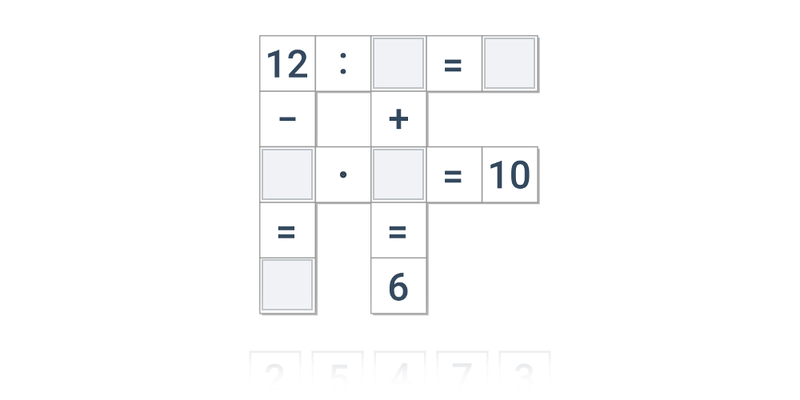
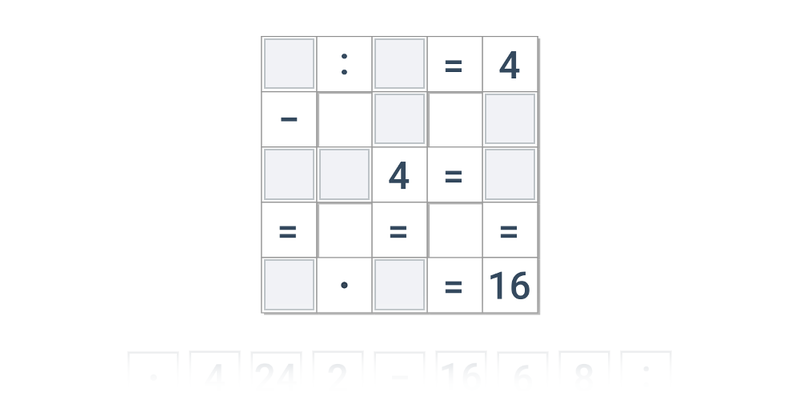
| Přesouvání | Magické čtverce | ||
| Psaná odpověď | Počty vrcholů, stěn, hran | ||
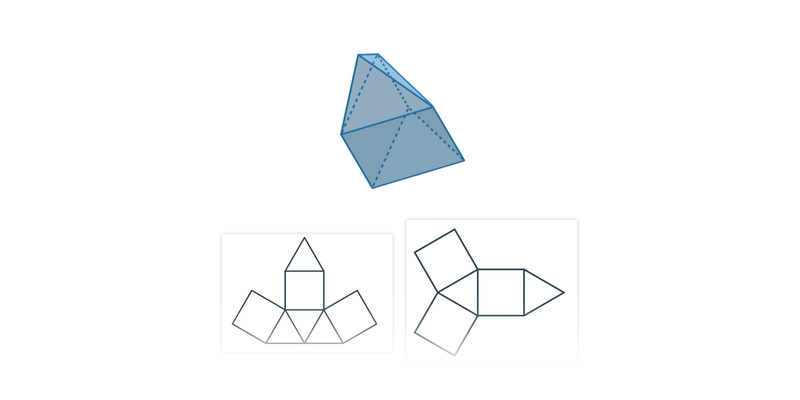
| Pexeso | 3D objekty z různých pohledů | ||
| Přesouvání | Síť krychle | ||
| Přesouvání | Síť krychle | ||
| Pexeso | Sítě těles | ||
| Rozhodovačka | Sítě těles | ||
| Přesouvání | Číselné křížovky | ||
| Přesouvání | Číselné křížovky | ||
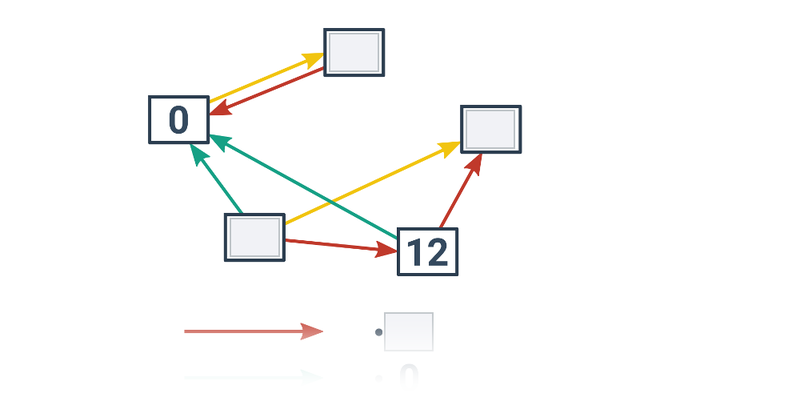
| Přesouvání | Doplň operaci | ||
| Přesouvání | Pavučiny s násobením |