
Krácení zlomků

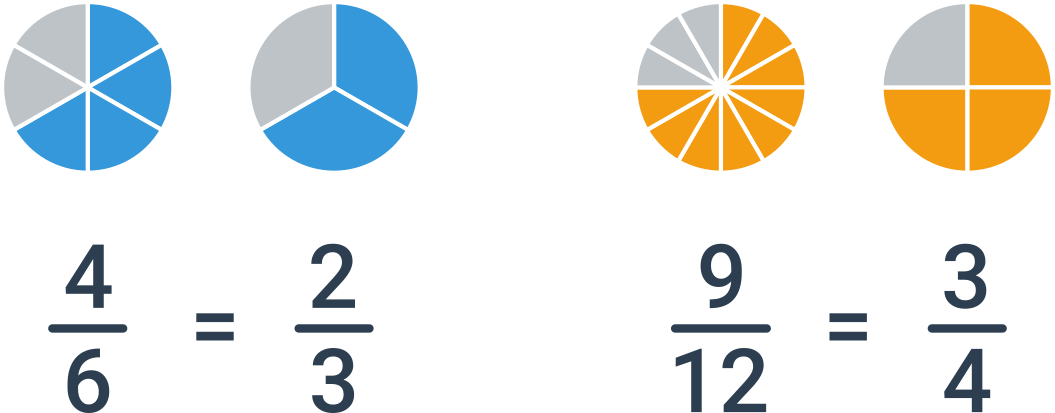
Stejnou hodnotu můžeme vyjádřit mnoha zlomky, například \frac23 = \frac46 = \frac{10}{15} = \frac{200}{300}. Jen jedno možné vyjádření ovšem považujeme za základní tvar. Zlomek je v základním tvaru, pokud jsou čitatel a jmenovatel nesoudělní, tj. nemají žádného společného dělitele kromě jedničky. V uvedeném příkladě je v základním tvaru zlomek \frac23.
Jako krácení zlomku se označuje operace, kdy čitatele i jmenovatele vydělíme stejným, nenulovým číslem. Krácení zachovává hodnotu zlomku. Pokud chceme zlomek převést do základního tvaru, krátíme největším společným dělitelem čitatele a jmenovatele.
Opačnou operací je rozšíření zlomku, kdy čitatele i jmenovatele vynásobíme stejným nenulovým číslem. Rozšíření zlomku se používá při sčítání a odčítání zlomků.
Příklady krácení zlomků
- Zlomek \frac{15}{28} je v základním tvaru, protože čísla 15 a 28 nemají společného dělitele (jsou nesoudělná).
- Zlomek \frac{25}{30} můžeme krátit číslem 5, čímž dostaneme zlomek \frac{5}{6}, který je v základním tvaru.
- Zlomek \frac{12}{18} můžeme krátit číslem 2, čímž dostaneme zlomek \frac{6}{9}. Pokud chceme krátit na základní tvar, najdeme největšího společného dělitele čísel 12 a 18, což je 6. Po krácení číslem 6 dostáváme zlomek \frac{2}{3}.
Komiks pro zpestření
Zavřít











