Exponenciální a logaritmické funkce
- Logaritmické funkce
Všechny souhrny - Grafy logaritmických funkcí
- Vlastnosti logaritmických funkcí
Předcházející
Cvičení
Pro logaritmickou funkci y=\log_ax platí:
- definiční obor D(f)=(0, \infty)
- obor hodnot H(f)=\R
- je prostá
- není periodická
- není sudá ani lichá
- nemá maximum ani minimum
- není omezená
Další vlastnosti závisí na hodnotě koeficientu a:
- pro a>1 je logaritmická funkce rostoucí
- pro a\in (0,1) je logaritmická funkce klesající
Příklad: vlastnosti funkce y=\log_2 x
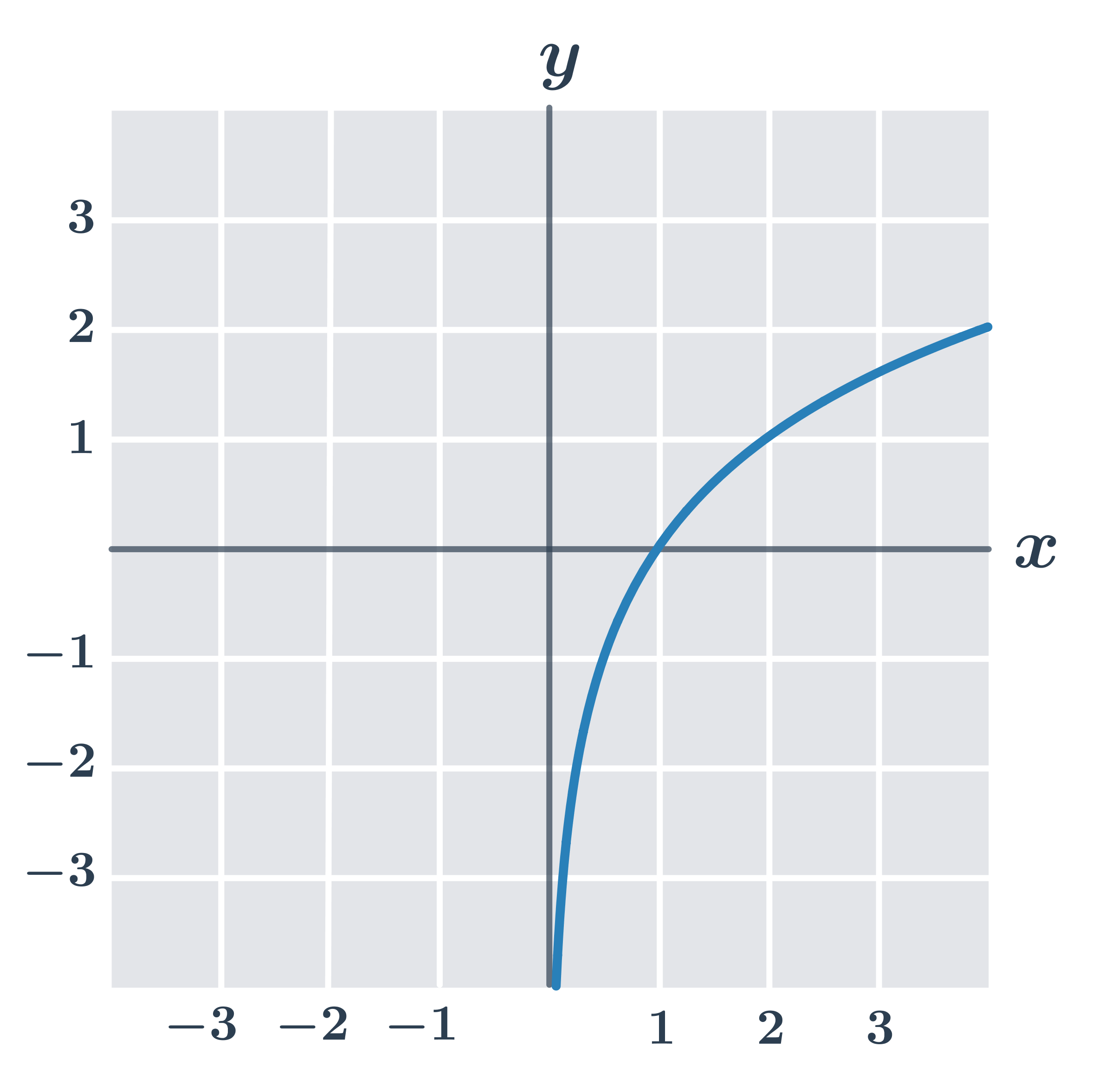
- definiční obor D(f)=(0, \infty)
- obor hodnot H(f)=\R
- je prostá
- je rostoucí
Příklad: vlastnosti funkce y=\log_{\frac{1}{2}} x
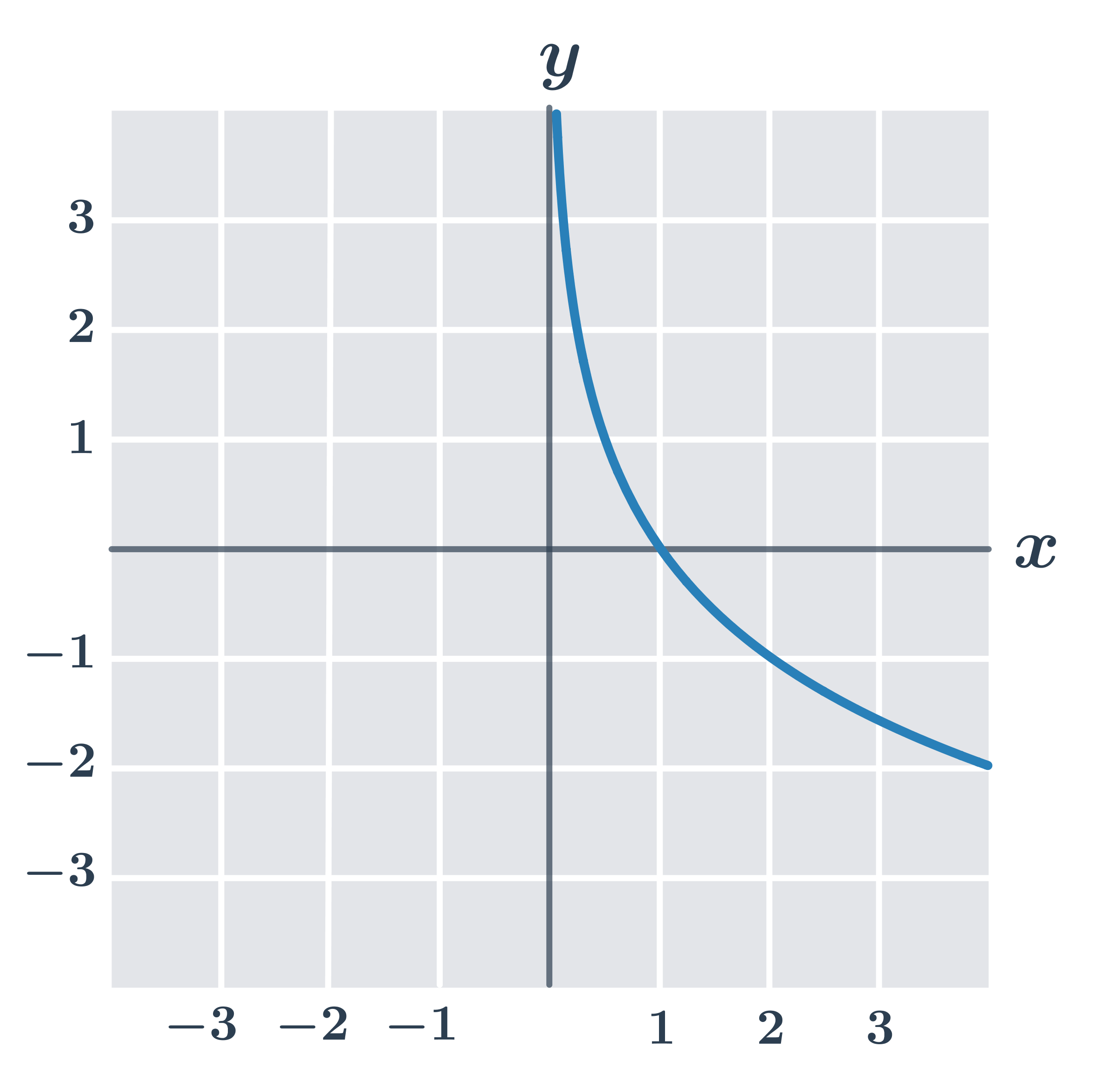
- definiční obor D(f)=(0, \infty)
- obor hodnot H(f)=\R
- je prostá
- je klesající
Příklad: vlastnosti funkce y=\log_3 (x+2)
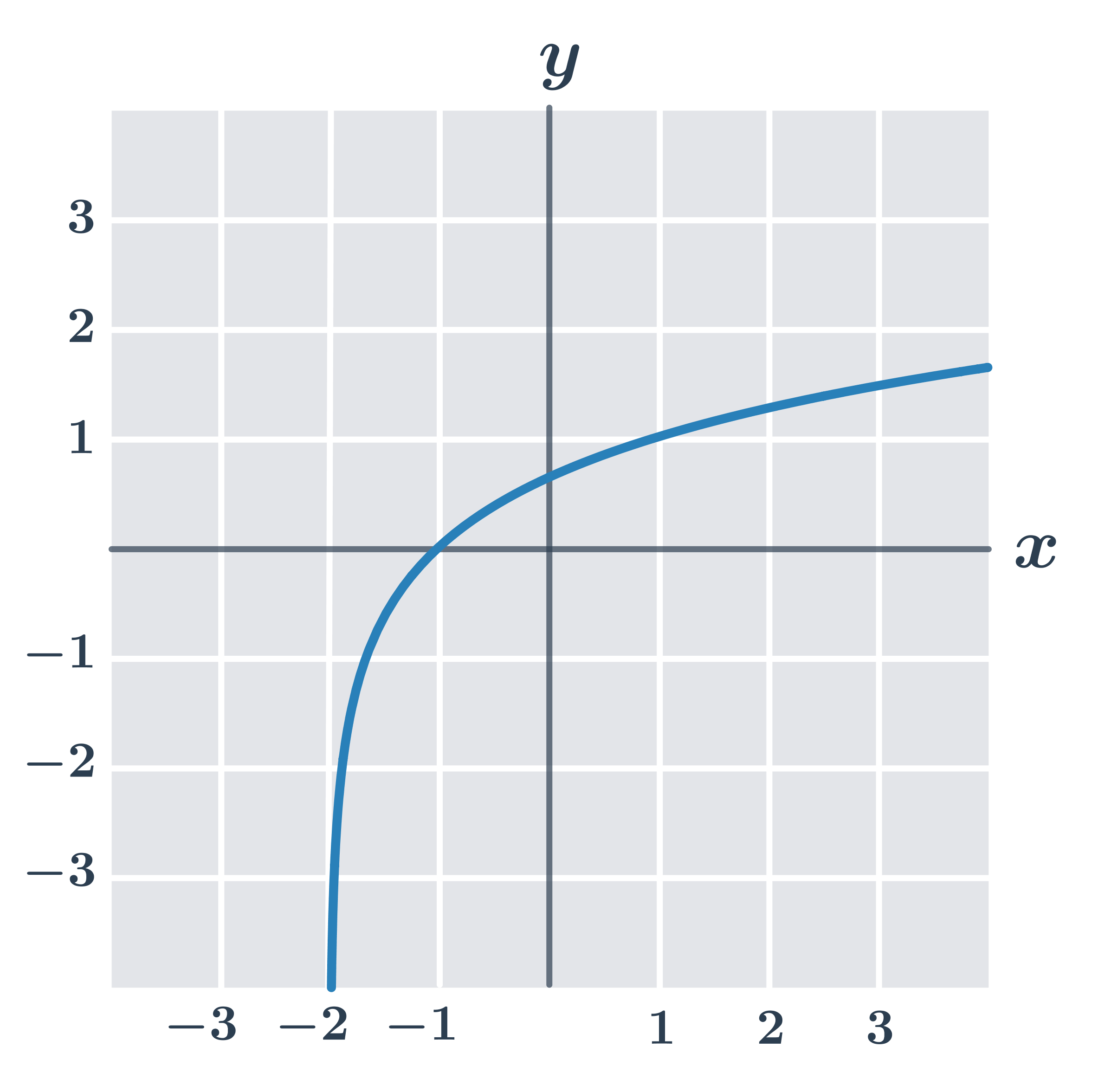
- definiční obor: D(f)=(-2, \infty) … výraz v logaritmu musí být kladný, tedy musí platit: x+2>0\Rightarrow x>-2
- obor hodnot H(f)=\R
- je prostá
- je rostoucí
- průsečík grafu s osou x je bod [-1,0] … najdeme jako řešení logaritmické rovnice: 0=\log_3(x+2). Podle pravidel pro počítání s logaritmy musí platit: 3^0=x+2\Rightarrow 1=x+2\Rightarrow x=-1
Souhrn mi pomohl
Souhrn mi nepomohl
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Vlastnosti logaritmických funkcí
Zobrazit souhrn tématu
těžké
Vlastnosti logaritmických funkcí (těžké) • G7W
Typicky zabere: 5 min.
