Výpis souhrnů
Logaritmické funkce
Podtémata
Logaritmické funkce
Funkce je logaritmická, pokud ji lze vyjádřit ve tvaru y=\log_a x, kde a je konstanta. Konstanta a se nazývá základ a může to být jakékoliv kladné reálné číslo kromě hodnoty 1, tedy a\in (0,1)\cup (1,\infty). Výraz x je argument.
Definičním oborem logaritmické funkce je množina všech kladných reálných čísel, oborem hodnot je množina všech reálných čísel.
NahoruVlastnosti logaritmických funkcí
Pro logaritmickou funkci y=\log_ax platí:
- definiční obor D(f)=(0, \infty)
- obor hodnot H(f)=\R
- je prostá
- není periodická
- není sudá ani lichá
- nemá maximum ani minimum
- není omezená
Další vlastnosti závisí na hodnotě koeficientu a:
- pro a>1 je logaritmická funkce rostoucí
- pro a\in (0,1) je logaritmická funkce klesající
Příklad: vlastnosti funkce y=\log_2 x
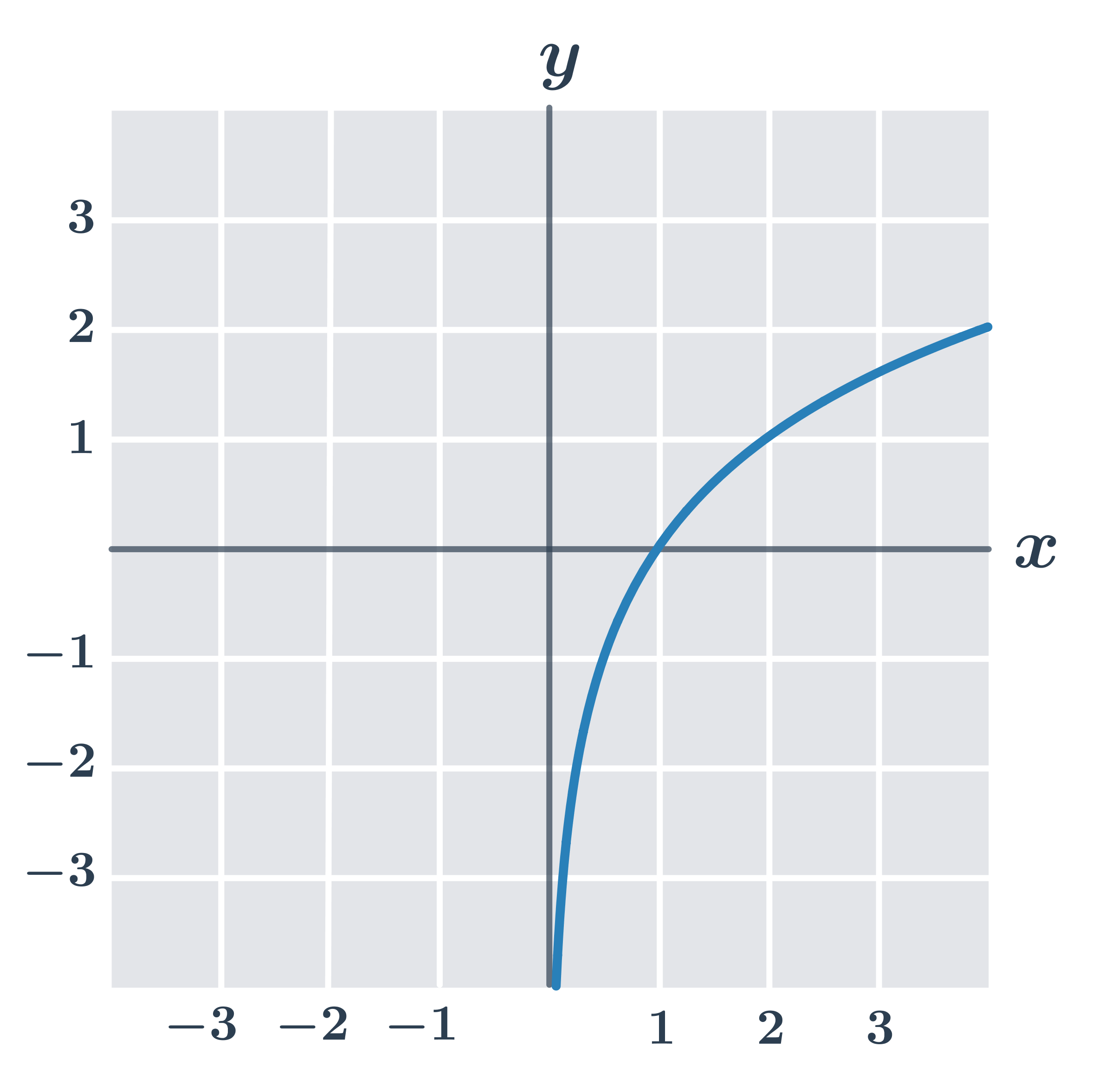
- definiční obor D(f)=(0, \infty)
- obor hodnot H(f)=\R
- je prostá
- je rostoucí
Příklad: vlastnosti funkce y=\log_{\frac{1}{2}} x
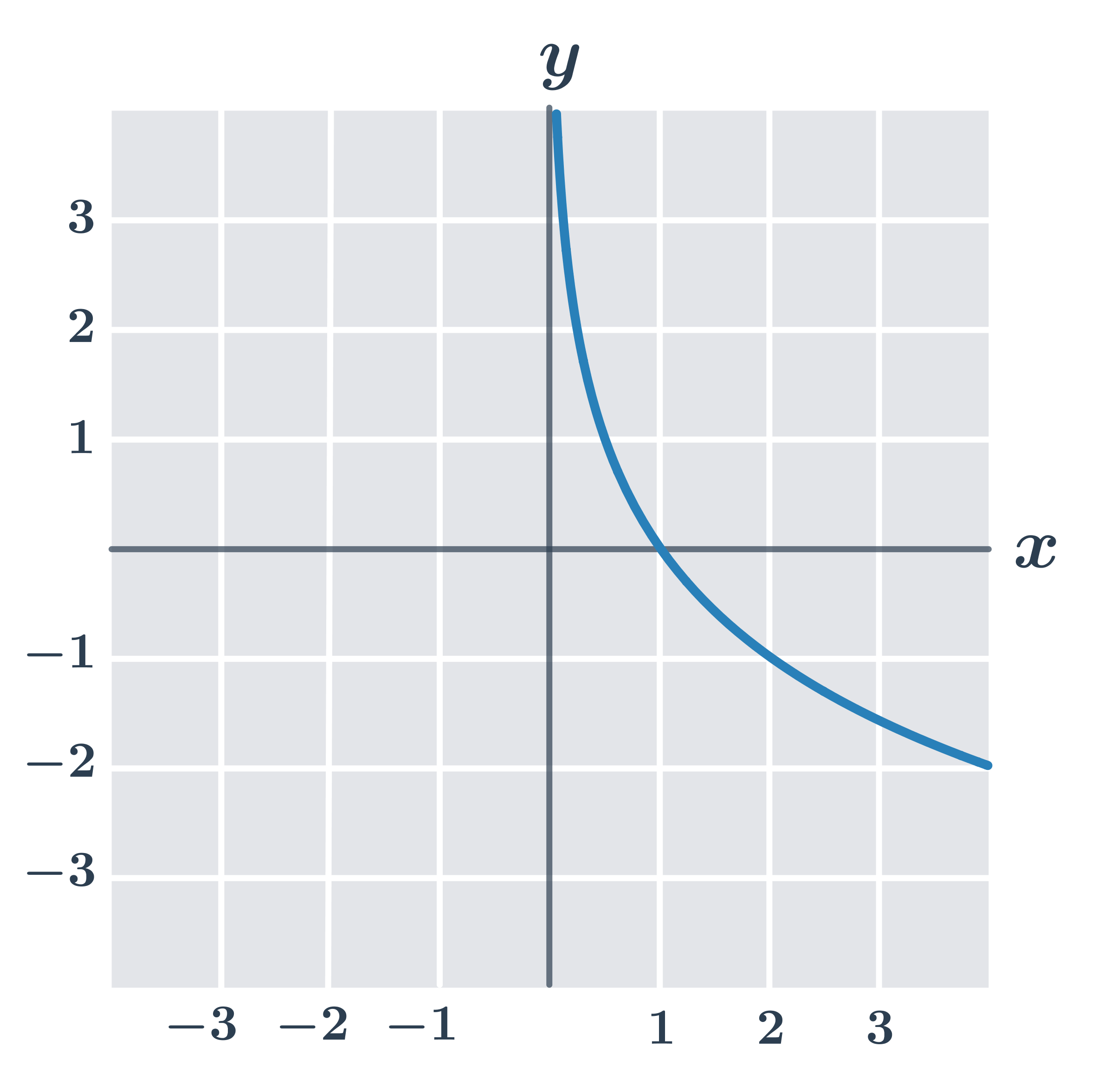
- definiční obor D(f)=(0, \infty)
- obor hodnot H(f)=\R
- je prostá
- je klesající
Příklad: vlastnosti funkce y=\log_3 (x+2)
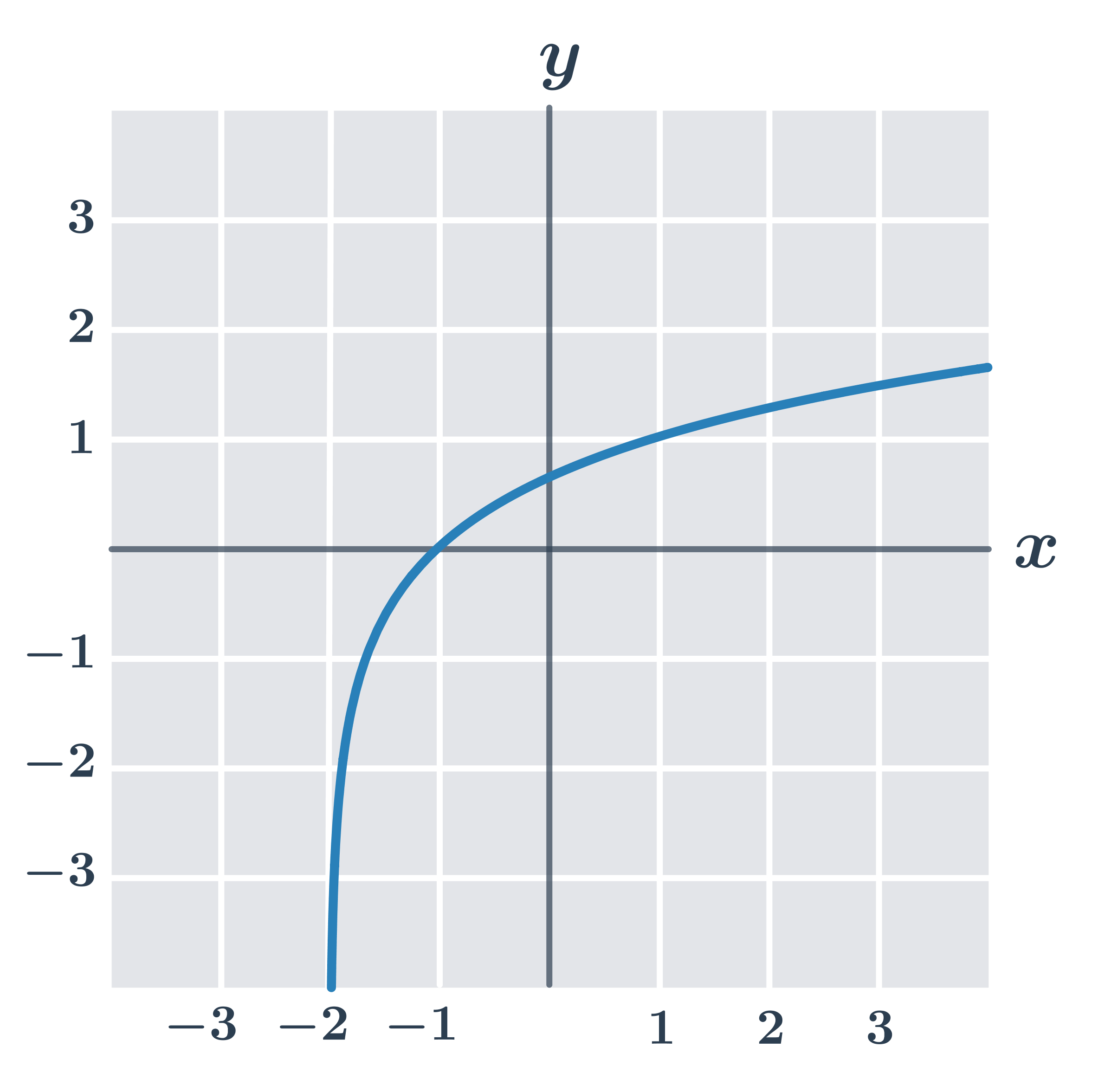
- definiční obor: D(f)=(-2, \infty) … výraz v logaritmu musí být kladný, tedy musí platit: x+2>0\Rightarrow x>-2
- obor hodnot H(f)=\R
- je prostá
- je rostoucí
- průsečík grafu s osou x je bod [-1,0] … najdeme jako řešení logaritmické rovnice: 0=\log_3(x+2). Podle pravidel pro počítání s logaritmy musí platit: 3^0=x+2\Rightarrow 1=x+2\Rightarrow x=-1
Grafy logaritmických funkcí
Logaritmická funkce je inverzní k exponenciální funkci o stejném základu. Grafy dvou navzájem inverzních funkcí jsou osově souměrné podle osy prvního kvadrantu (tj. přímky splňující x=y).
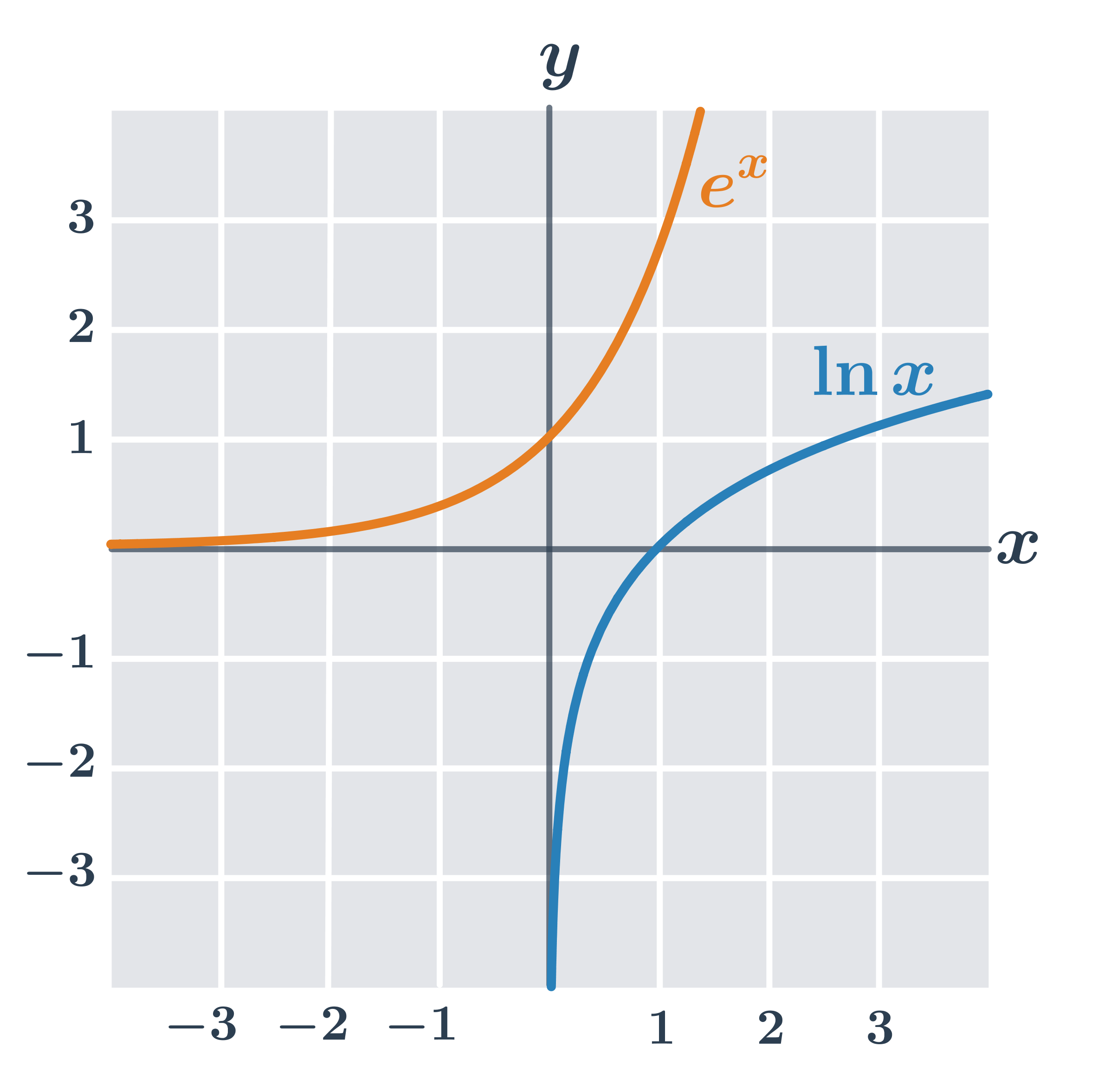
Graf každé logaritmické funkce tvaru y=\log_a x prochází bodem [1,0], protože pro libovolnou konstantu a platí: \log_a 1=0. Na obrázku vidíme grafy logaritmických funkcí s různými základy 2, e, 10.
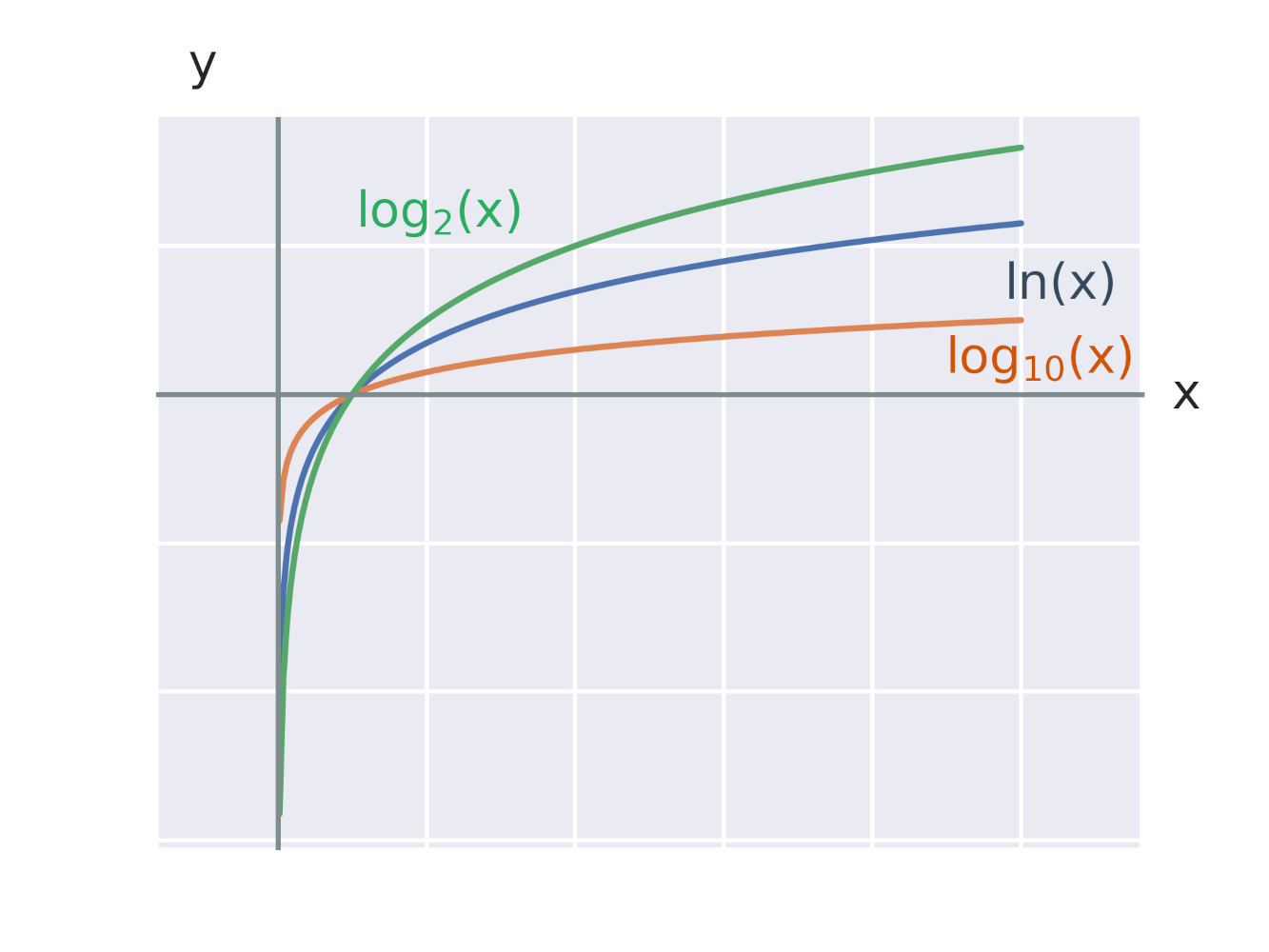
Značení některých význačných logaritmických funkcí:
| funkce | popis | další možná značení |
|---|---|---|
| \log_a x | obecně logaritmus x o základu a pro nějaké a >0, a\neq 1 | |
| \ln x | přirozený logaritmus x, tj. logaritmus x o základu e | v angl. textech někdy \log x |
| \log x | dekadický logaritmus x, tj. logaritmus x o základu 10 | \log_{10}x |
| \log_2 x | binární logaritmus x, tj. logaritmus x o základu 2 | někdy se objevuje \mathrm{lb}\;x |
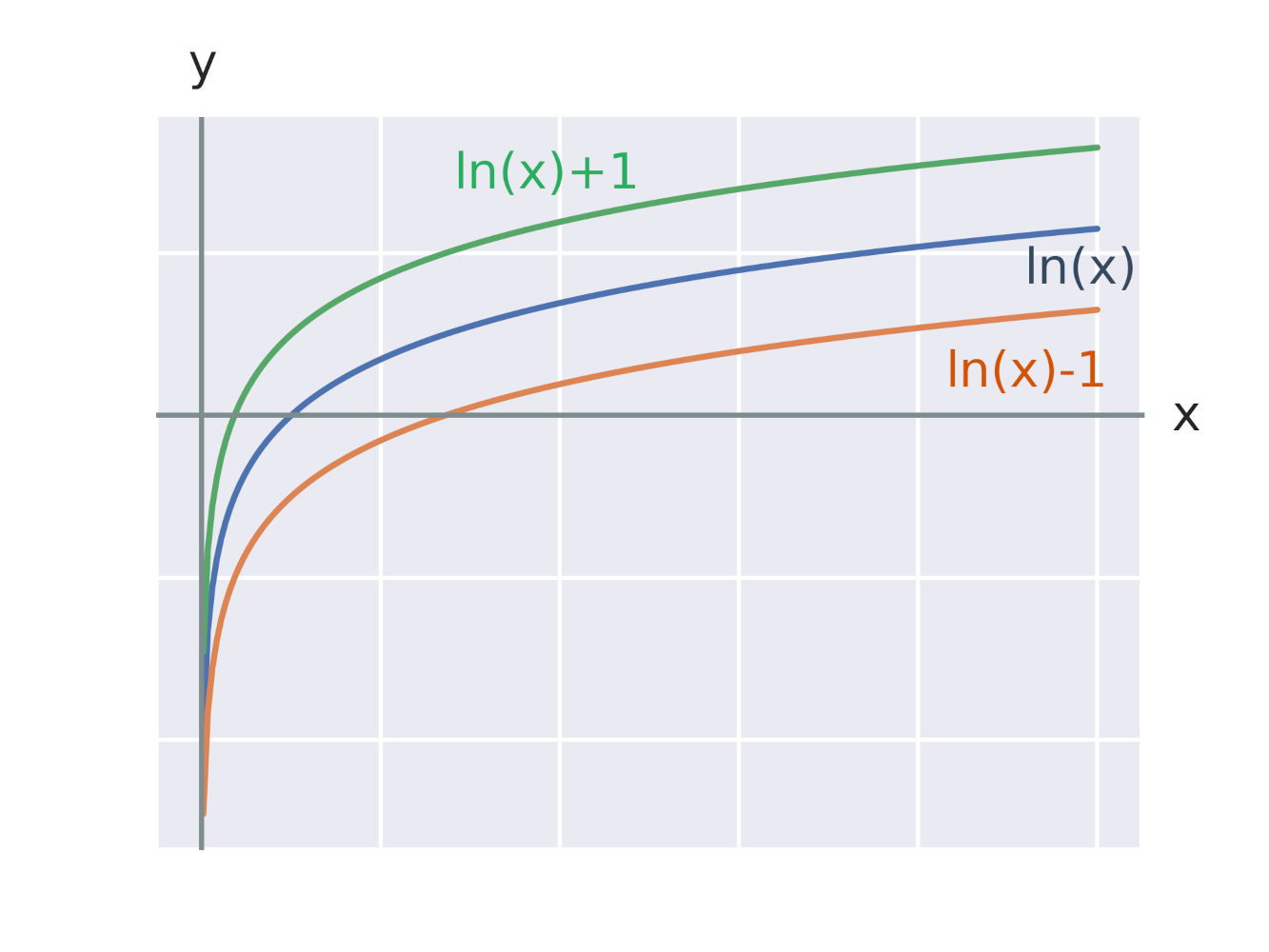
Efekt přičtení konstanty k logaritmické funkci
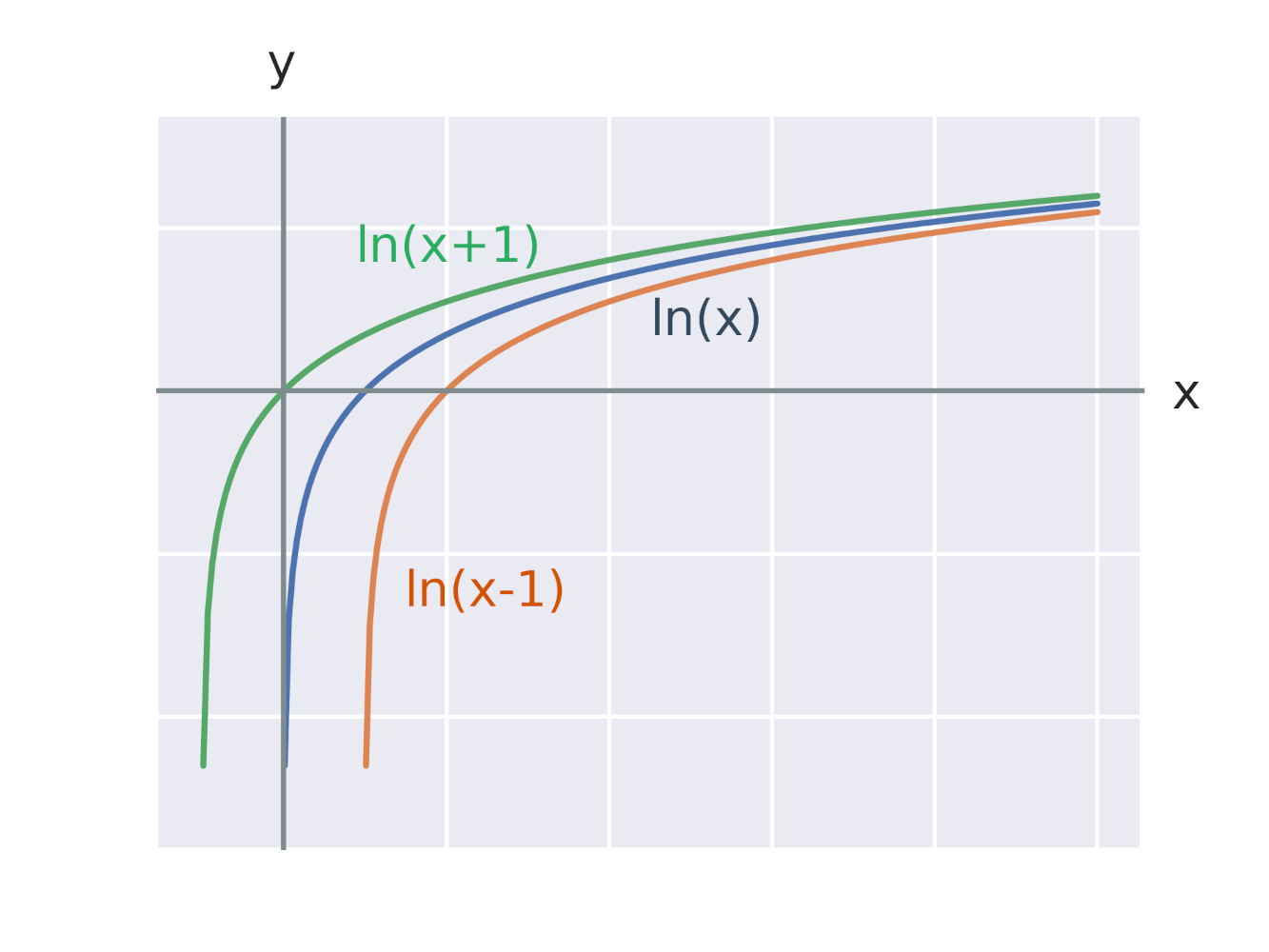
Efekt přičtení konstanty k argumentu logaritmické funkce
Efekt vynásobení logaritmické funkce konstantou
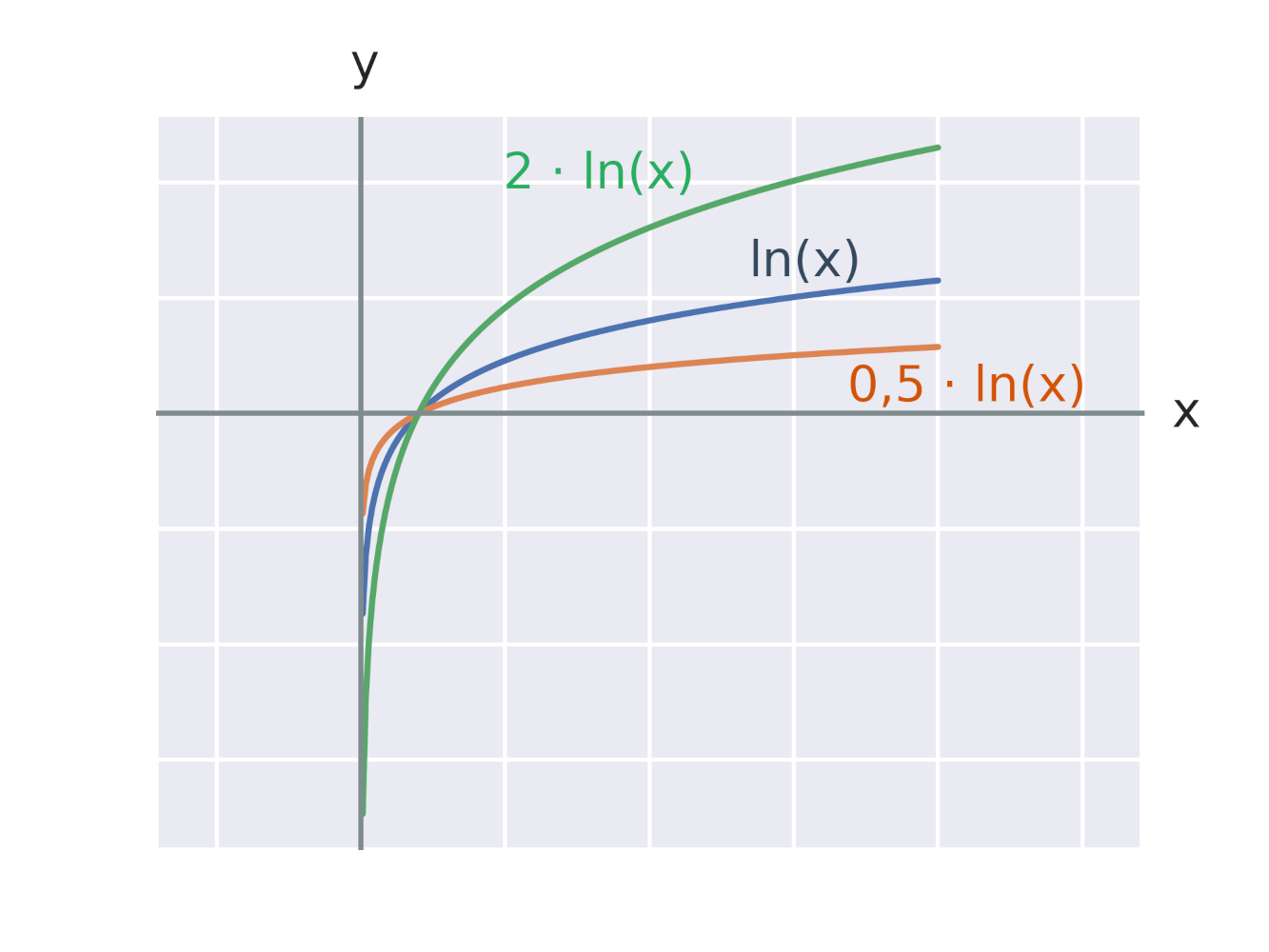
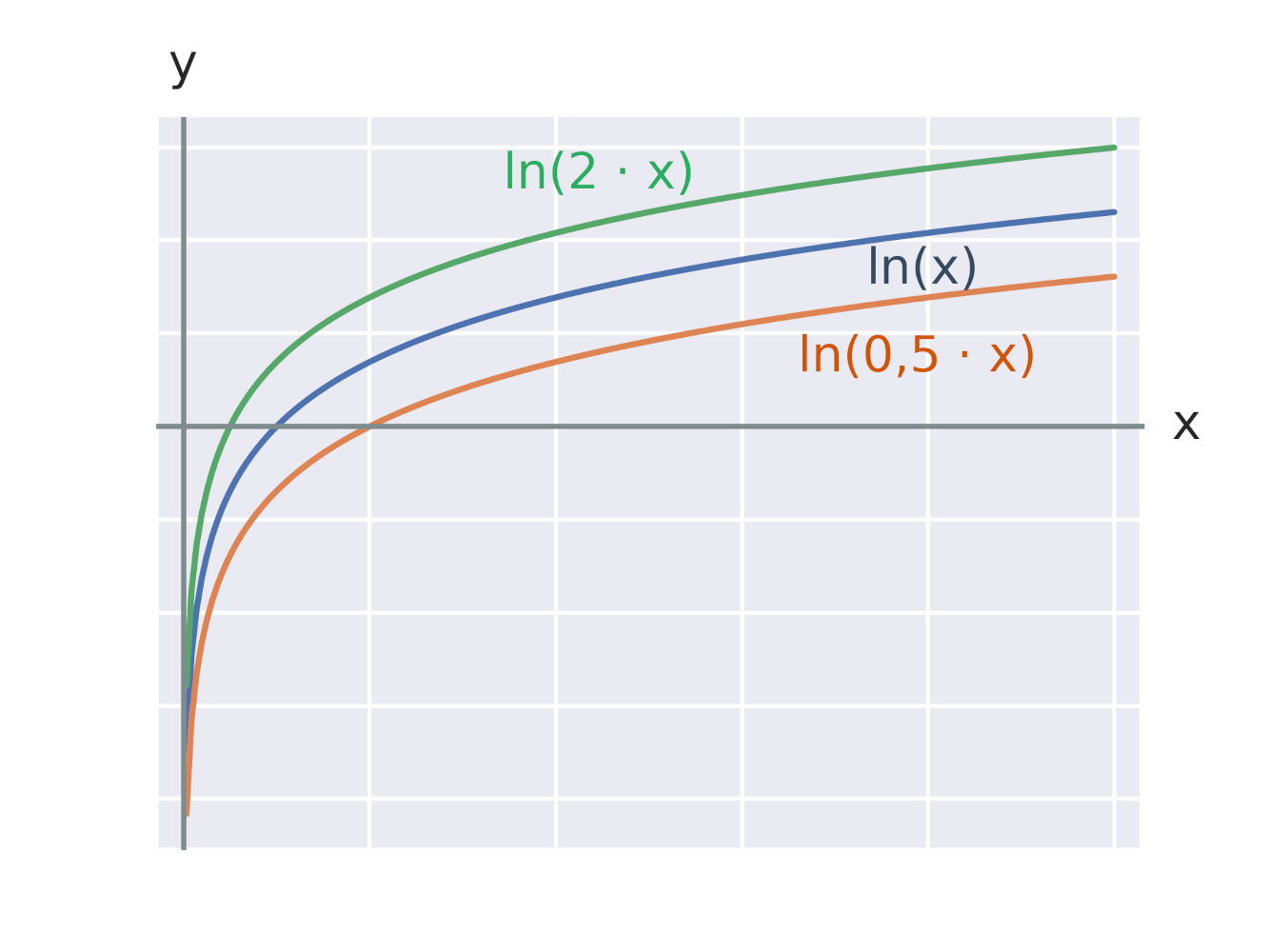
Efekt vynásobení argumentu logaritmické funkce konstantou