Pythagorova věta – 6. třída

Pythagorova věta popisuje vztah, který platí mezi délkami stran pravoúhlého trojúhelníku: Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami.

Pythagorovu větu můžeme zapsat vztahem c^2 = a^2 + b^2, kde c označuje délku přepony pravoúhlého trojúhelníka a délky odvěsen jsou a, b. Platí i opačný směr: Pokud má trojúhelník strany délek a, b, c, které splňují rovnost c^2 = a^2 + b^2, pak musí jít o pravoúhlý trojúhelník s přeponou c.

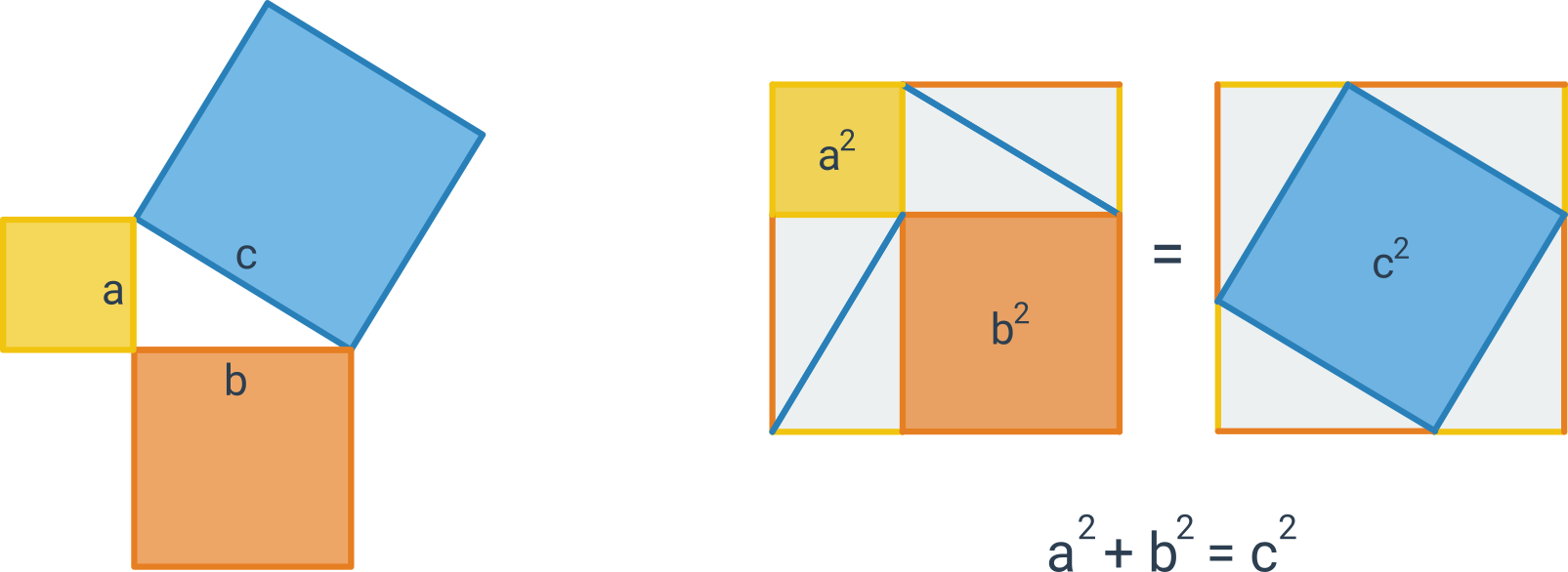
Následující obrázek znázorňuje graficky znění věty a také „obrázkový důkaz“ této věty:

Procvičování Pythagorovy věty máme rozdělené do dvou podtémat:

• Základní použití – základní aplikace vzorce a^2+b^2=c^2, výpočty délky strany pravoúhlého trojúhelníku při znalosti zbylých dvou stran
• Aplikace – využití Pythagorovy věty v různých geometrických případech (např. výška trojúhelníku, uhlopříčka kvádru) a slovních úlohách