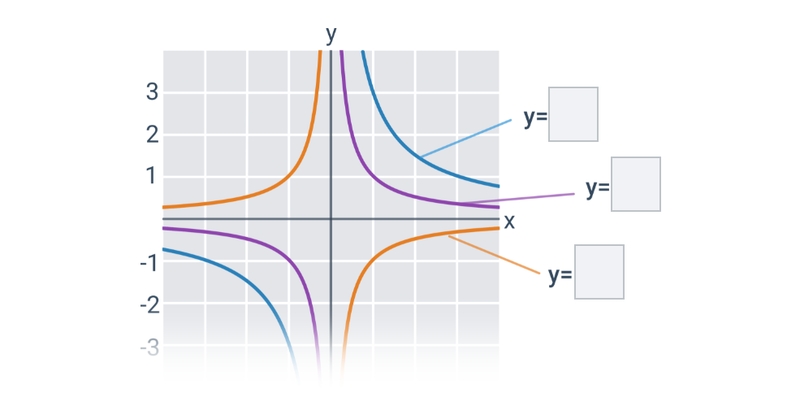
Lineární lomené funkce
G4KLineární lomenou funkci můžeme vyjádřit jako podíl dvou lineárních funkcí, tedy ve tvaru
f:y =\frac{ax+b}{cx+d},
kde a,b,c,d jsou konstanty.
Definičním oborem lineární lomené funkce je množina všech reálných čísel kromě hodnoty, ve které by jmenovatel zlomku \frac{ax+b}{cx+d} byl nulový:
D(f)=\mathbb{R} - \{-\frac{d}{c}\}
Úpravou podmínky pro nenulovost jmenovatele zlomku dostaneme vyjádření definičního oboru pomocí nerovnice: cx+d\neq0\Rightarrow x\neq -\frac{d}{c}
Kdy je funkce nelineární a nekonstantní (a graf je hyperbola, nikoliv přímka)
K tomu, aby f:y=\frac{ax+b}{cx+d} nebyla lineární ani konstantní funkce, musí být splněno několik podmínek. Pro konstanty a,b,c,d musí platit: c\neq0 a bc-ad\neq0.
- pro c=0 bychom měli lineární funkci danou rovnicí y =\frac{a}{d}\cdot x+\frac{b}{d}
- pro bc-ad=0 bychom měli konstantní funkci y =\frac{a}{c}
Vysvětlení podmínky bc-ad\neq0
| Pro lineární lomenou funkci danou předpisem \frac{ax+b}{cx+d} provedeme dělení čitatele zlomku \frac{ax+b}{cx+d} jeho jmenovatelem: |
| \begin{array}{lrrrr} \hspace{0.3cm}(\hspace{0.4cm}ax+\hspace{0.47cm}b)&:&(cx+d)&=&\frac{a}{c}\\\underline{-( \frac{a}{c}\cdot cx+\frac{a}{c}\cdot d)\hspace{0.5cm}}& \\ \hspace{1.05cm}0+b-\frac{a}{c}\cdot d\\ \end{array} |
| Vyšel nám tedy podíl \frac{a}{c} a zbytek b-\frac{a}{c}\cdot d. |
| Pokud by platilo b-\frac{a}{c}\cdot d=0, mohli bychom funkci y =\frac{ax+b}{cx+d} zapsat zjednodušeně ve tvaru y =\frac{a}{c} a to není lineární lomená funkce, ale funkce konstantní. |
| Abychom měli lineární lomenou funkci, musí tedy platit b-\frac{a}{c}\cdot d\neq0. Tuto podmínku můžeme vynásobením obou stran hodnotou c upravit na tvar: bc-ad\neq0 |
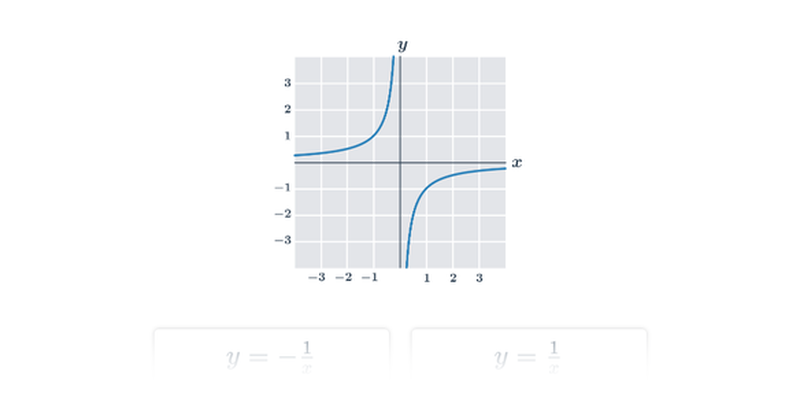
Speciálním případem lineární lomené funkce je nepřímá úměrnost vyjádřená ve tvaru y =\frac{k}{x}.
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.