Výpis souhrnů
Kruh a kružnice
Podtémata
Kruh a kružnice
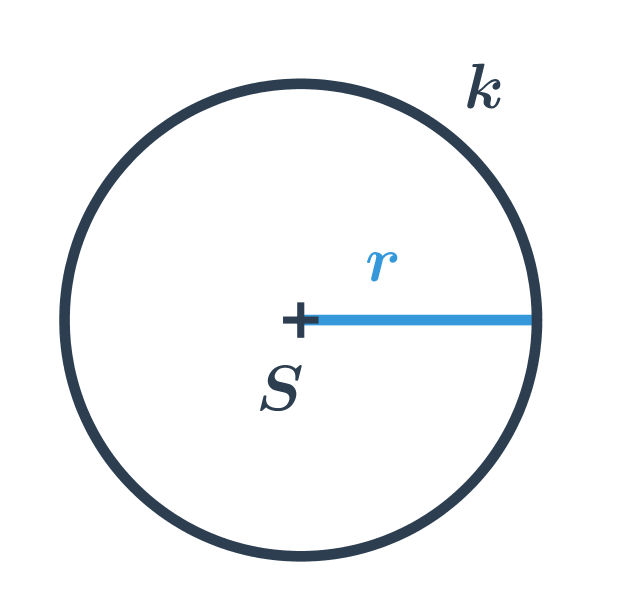
Kružnice s daným středem S a poloměrem r je tvořena všemi body v rovině, které jsou od středu vzdáleny přesně o r. U každého bodu v rovině pak můžeme určit, kde leží:
- na kružnici (jejich vzdálenost od S je rovna r)
- ve vnitřní oblasti kružnice (jejich vzdálenost od S je menší než r, tyto body neleží na kružnici)
- ve vnější oblasti kružnice (jejich vzdálenost od S je větší než r, tyto body také neleží na kružnici)
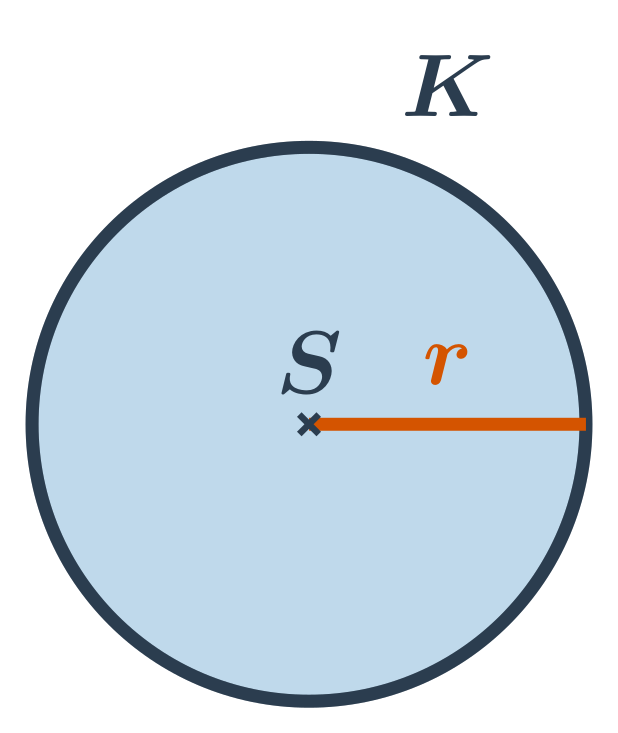
Kruh s daným středem S a poloměrem r je tvořen všemi body v rovině, které jsou od středu vzdáleny nejvýše o r. Kruh s daným středem a poloměrem je tedy sjednocení kružnice se stejným středem a poloměrem a její vnitřní oblasti. Střed S kruhu je bod, který patří do kruhu. (Zatímco střed kružnice neleží na kružnici, ale v její vnitřní oblasti.)
Pojmy související s kružnicí
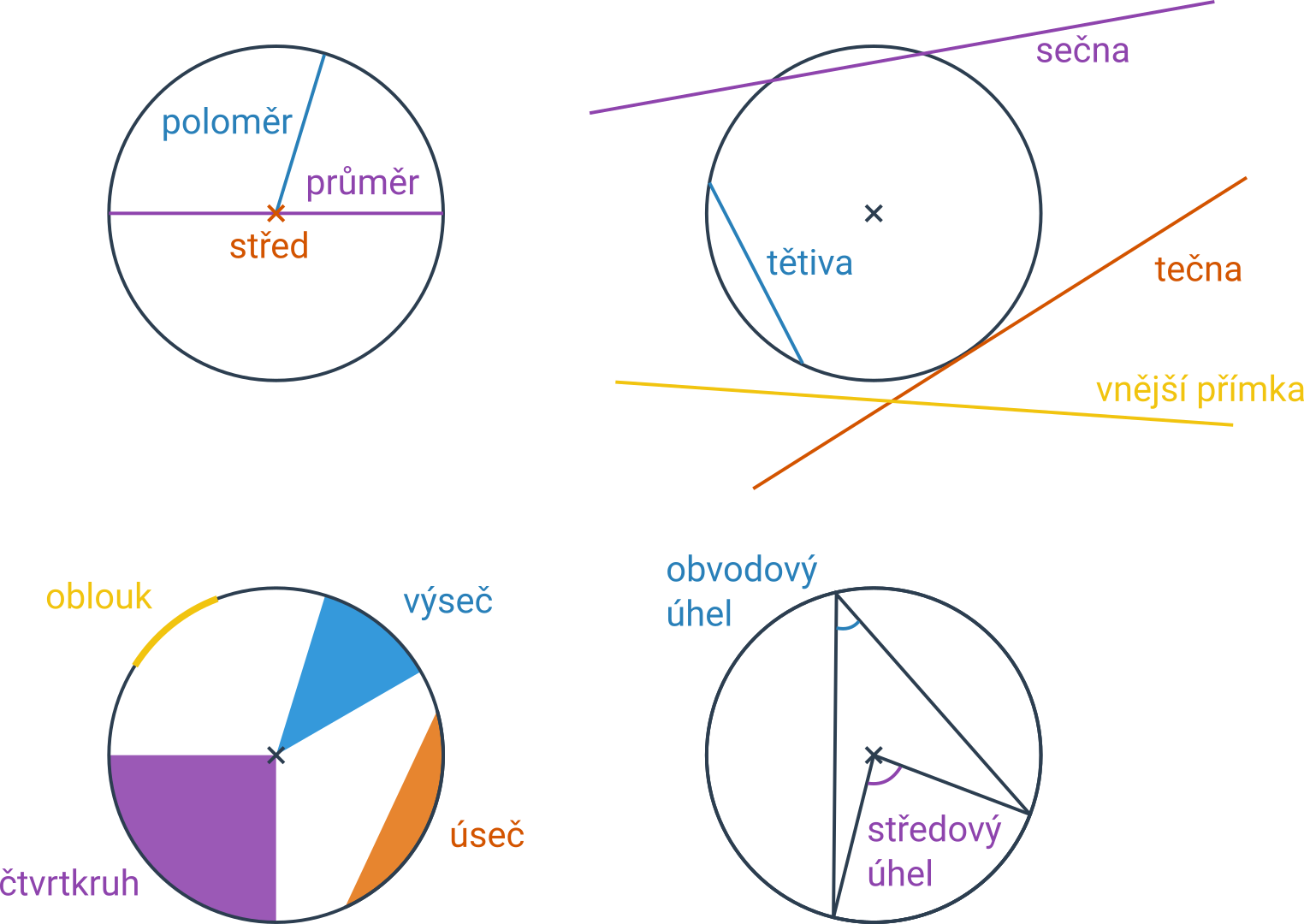
| poloměr | jejíž jeden koncový bod leží na kružnici a druhý koncový bod ve středu kružnice |
| průměr | úsečka, která prochází středem kružnice a jejíž oba krajní body leží na této kružnici |
| tečna | přímka, která se kružnice dotýká právě v jednom bodě |
| sečna | přímka, která kružnici protíná ve dvou bodech |
| vnější přímka | přímka, která kružnici neprotíná |
| tětiva | úsečka spojující dva body na kružnici |
| kruhová výseč | část kruhu příslušná středovému úhlu |
| mezikruží | plocha mezi dvěma soustřednými kružnicemi |
| půlkruh | výseč příslušná přímému úhlu (180°) |
| čtvrtkruh | výseč příslušná pravému úhlu (90°) |
| úseč | část kruhu vymezená tětivou a kruhovým obloukem vzniklá rozdělením kruhu sečnou |
| středový úhel | úhel, jehož vrcholem je střed kružnice a jehož ramena procházejí krajními body oblouku |
| obvodový úhel | úhel, jehož vrchol leží na kružnici a ramena procházejí krajními body oblouku |
Komiks pro zpestření

Obvod kruhu, délka kružnice
Vzorec pro obvod kruhu
Obvod kruhu (i kružnice) o poloměru r je o=2\pi r. Pro průměr d platí o = \pi d.
Konstanta \pi se nazývá též Ludolfovo číslo. \pi je iracionální číslo, což znamená, že nejde vyjádřit zlomkem ani zapsat přesně v desítkové soustavě. Přibližná hodnota \pi je 3,141 592 65.
Při výpočtu obvodu kruhu dáváme dobrý pozor na to, zda vycházíme ze znalosti poloměru r nebo průměru d = 2r. Záměna průměru za poloměr je častou chybou.
Intuice
Základní intuici za vzorcem pro výpočet obvodu kruhu přibližuje níže uvedený obrázek. Obvod oranžového čtverce je 8\cdot r. Obvod kruhu je „o trochu menší“ – je to 2\pi \cdot r \approx 6{,}3 \cdot r.

Příklady: obvod kruhu
- Mějme kruh o poloměru 3 cm. Jeho obvod je 2\pi \cdot 3 \approx 2 \cdot 3{,}14 \cdot 3 \approx 18{,}8 cm.
- Kružnice o průměru 2 cm má délku \pi \cdot 2 \approx 6,3 cm.
- Středový kruh na fotbalovém hřišti má poloměr 9{,}1 metru. Pokud jej chceme obejít po jeho okrajové čáře, ujdeme 2 \pi \cdot 9{,}1 \approx 57 metrů.
Obsah kruhu
Vzorec pro obsah kruhu
Obsah kruhu o poloměru r je S=\pi r^2. Pro průměr d platí S = \frac{1}{4} \pi d^2.
Konstanta \pi se nazývá též Ludolfovo číslo. \pi je iracionální číslo, což znamená, že nejde vyjádřit zlomkem ani zapsat přesně v desítkové soustavě. Přibližná hodnota \pi je 3,141 592 65.
Při výpočtu obsahu kruhu dáváme dobrý pozor na to, zda vycházíme ze znalosti poloměru nebo průměru. Záměna průměru za poloměr je častou chybou.
Intuice
Základní intuici za vzorcem pro výpočet obsahu kruhu přibližuje níže uvedený obrázek. Žluté čtverce mají obsah r^2. Oranžový čtverec se skládá ze čtyř žlutých čtverců, takže má obsah 4\cdot r^2. Kruh má „o trochu menší“ obsah než oranžový čtverec, což odpovídá tomu, že obsah kruhu je přibližně 3{,}14 \cdot r^2.

Příklady
- Mějme kruh o poloměru 3 cm. Jeho obsah je \pi \cdot 3^2 \approx 3{,}14\cdot 9 \approx 28,3 cm².
- Uvažujme kružnici o průměru 2 cm. Její vnitřní oblast má obsah \frac{1}{4} \pi \cdot 2^2 = \pi \approx 3,14 cm².
- Středový kruh na fotbalovém hřišti má poloměr 9{,}1 metru. Pokud bychom chtěli veškerou trávu v kruhu nabarvit na růžovo, museli bychom nabarvit \pi \cdot 9{,}1^2 \approx 260 m² trávy.
Komiks pro zpestření
Úhly a kružnice
Středový úhel
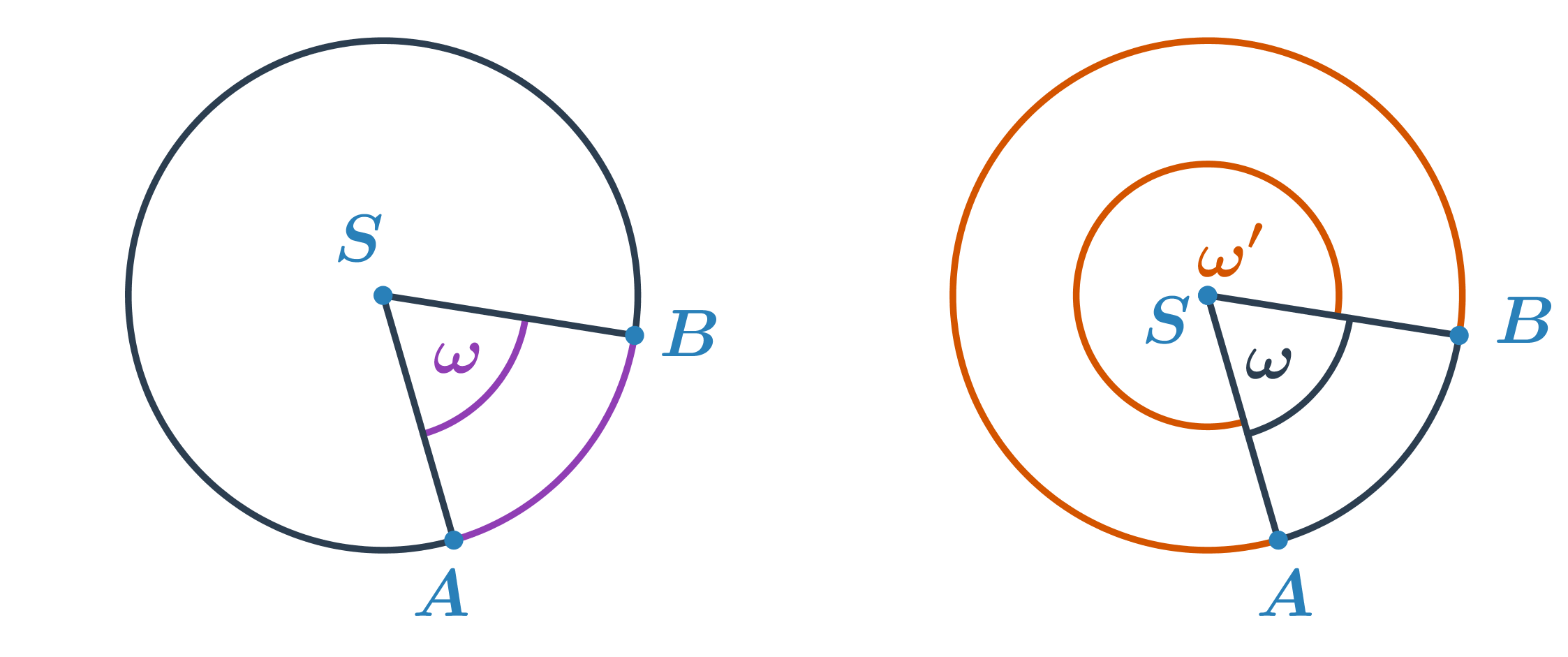
- Úhel s vrcholem ve středu S kružnice k, jehož ramena procházejí krajními body A, B oblouku kružnice k.
- Pro každé dva body na kružnici lze určit dva středové úhly. Každý přísluší tomu oblouku, který v daném úhlu leží.
Obvodový úhel
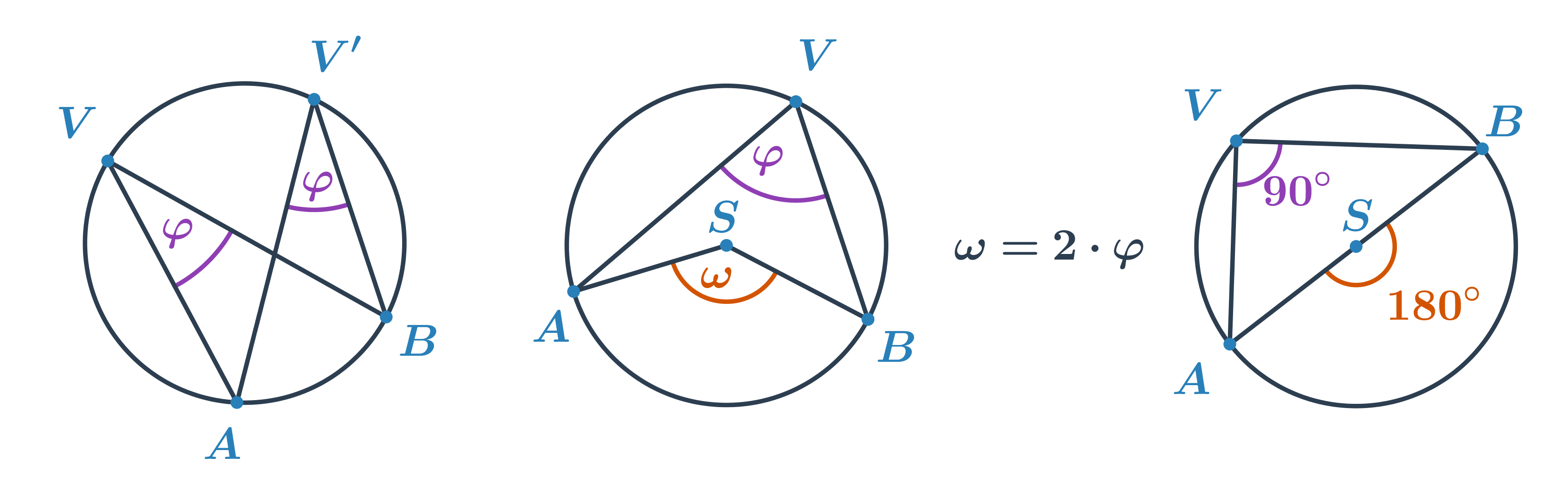
- Úhel, jehož vrchol V leží na kružnici k a jeho ramena procházejí body A, B oblouku kružnice k (A \neq V \neq B)
- Všechny obvodové úhly příslušné oblouku AB s vrcholem V, který na oblouku neleží, mají stejnou velikost.
- Velikost středového úhlu \omega se rovná dvojnásobku velikosti obvodového úhlu \varphi příslušného ke stejnému oblouku, \omega = 2\cdot\varphi.
- Thaletova věta: Obvodový úhel nad průměrem kružnice je pravý.
Úsekový úhel
- Úhel, jenž svírá tětiva AB kružnice k s tečnou t kružnice v bodě A nebo B.
- Velikost úsekového úhlu je stejná jako velikost obvodového úhlu nad obloukem AB.
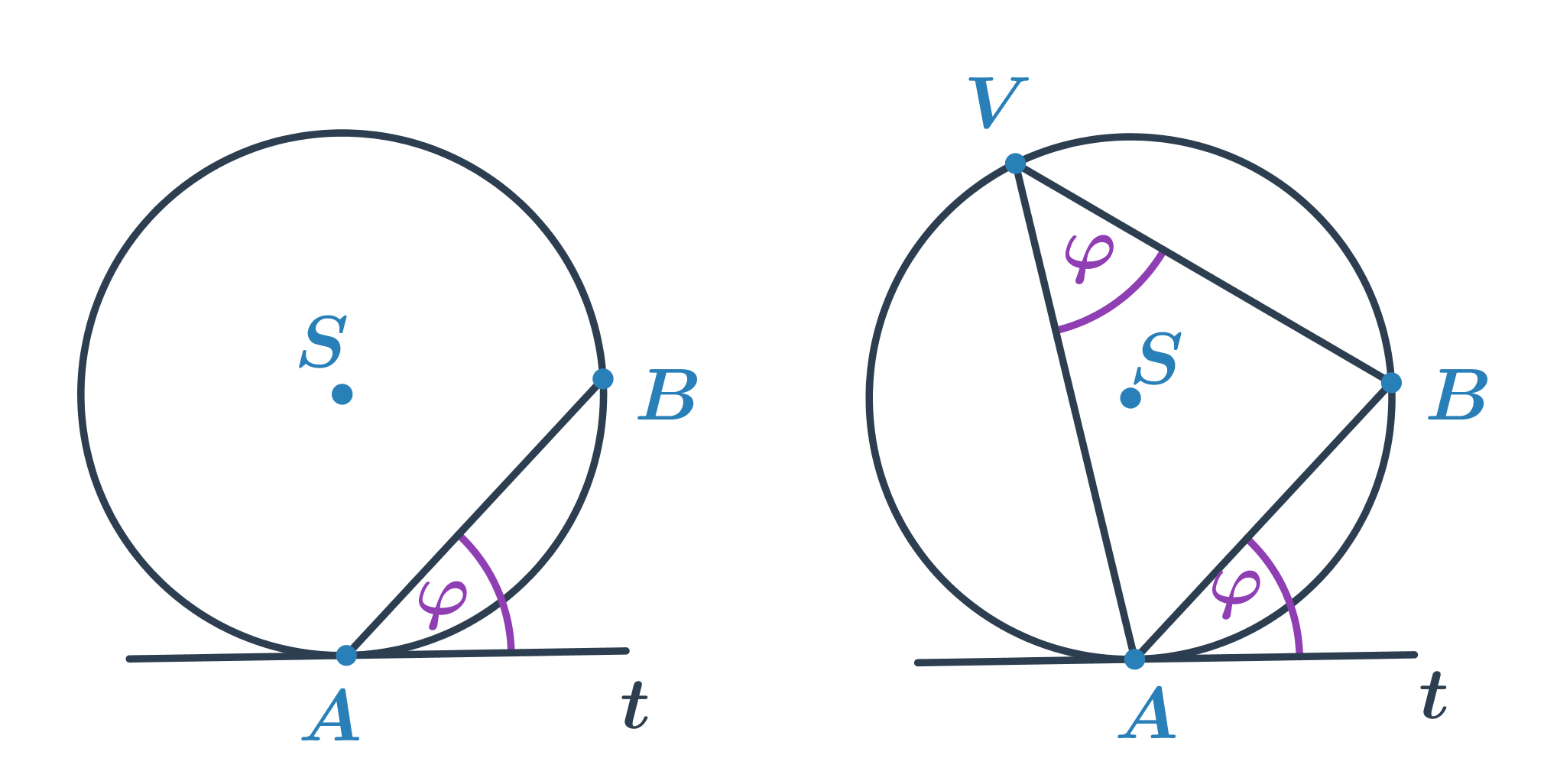
Příklad 1: Určete velikost úhlu
Určete velikost oranžového úhlu.
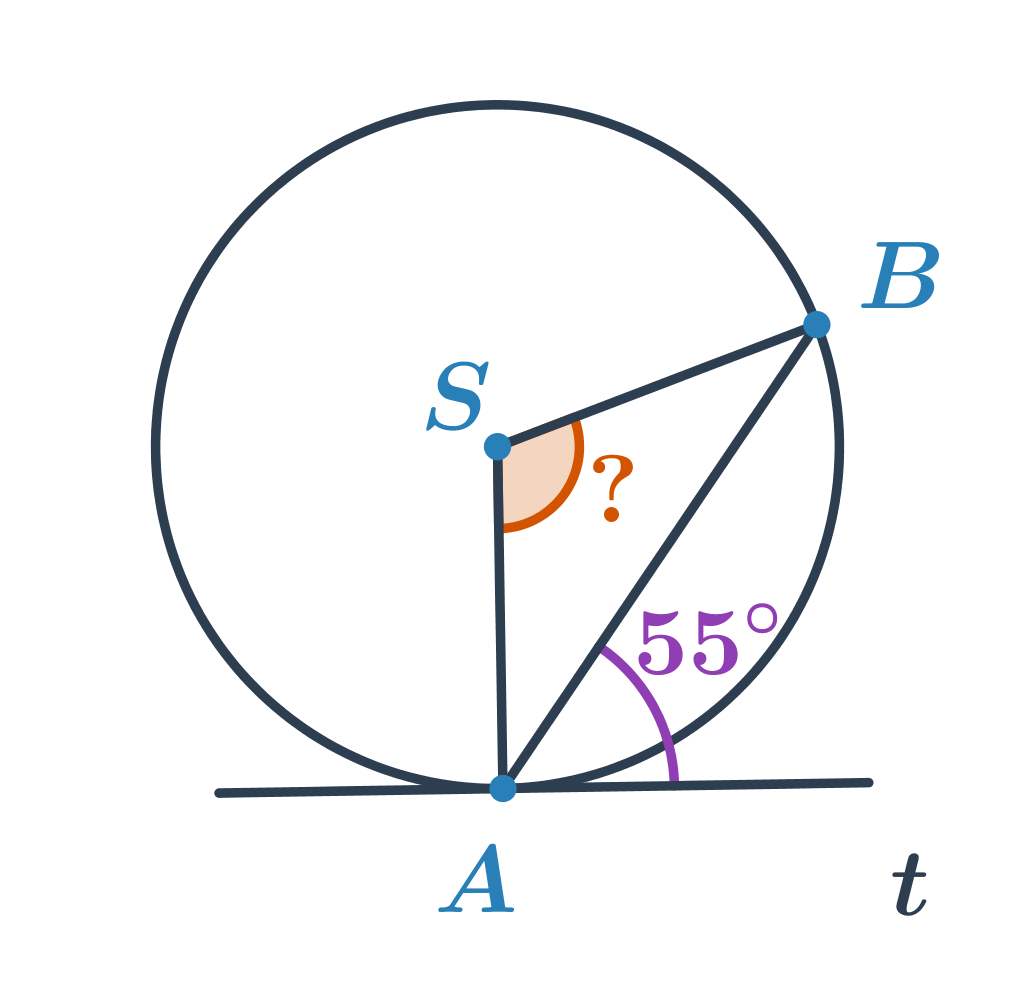
Úhel o velikosti 55^\circ je úsekový úhel příslušný tětivě AB. Víme, že velikosti úsekového a příslušného obvodového úhlu jsou stejné, tedy 55^\circ. Neznámý úhel je středový úhel příslušný menšímu oblouku AB. Jeho velikost je dvojnásobkem velikosti obvodového úhlu, tedy 2\cdot55^\circ=110^\circ.
Příklad 2: Určete velikost úhlu
Určete velikost oranžového úhlu.
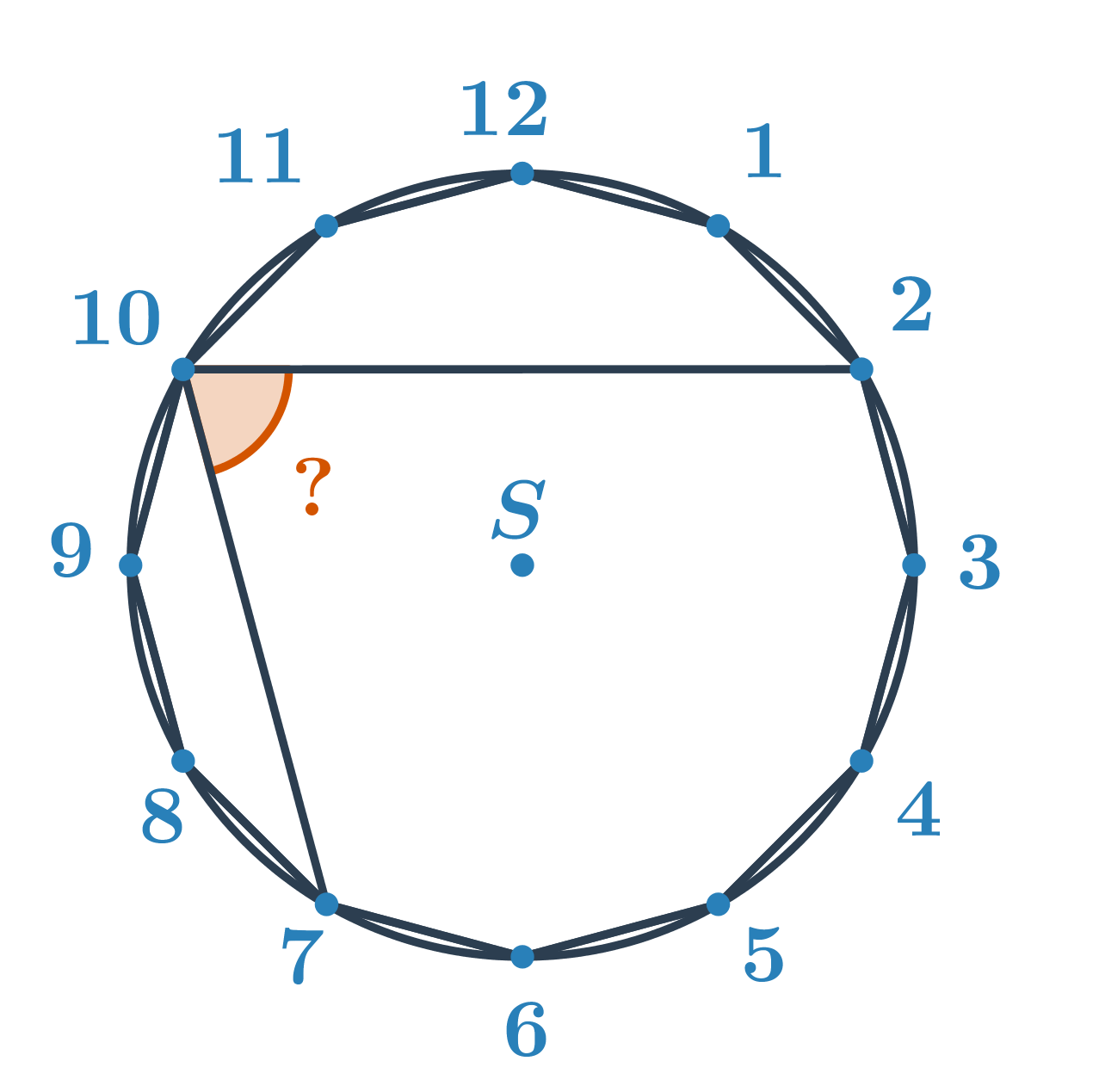
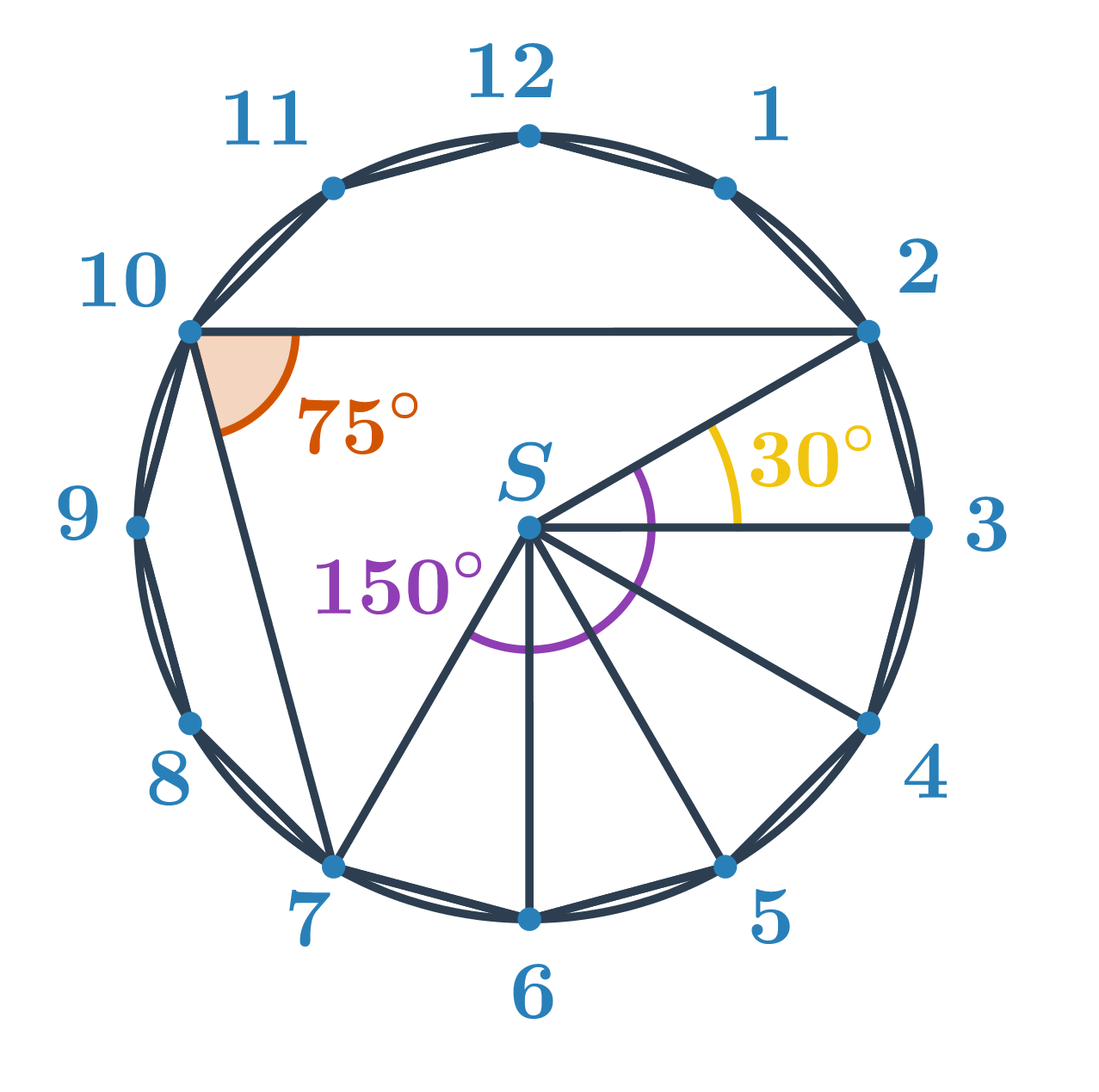
Neznámý úhel je obvodovým úhlem nad menším obloukem s koncovými body 2 a 7. Určíme velikost příslušného středového úhlu. Z kapitoly úhly a mnohoúhelníky víme, že velikost středového úhlu pravidelného n-úhelníku je \frac{360^\circ}{n}. Pro pravidelný dvanáctiúhelník je tedy úhel mezi spojnicemi dvou vedlejších vrcholů a středu \frac{360^\circ}{12}=30^\circ. Středový úhel příslušný oblouku 2 a 7 je pak 5\cdot30^\circ=150^\circ. Hledaný obvodový úhel má poloviční velikost, tedy 150^\circ:2=75^\circ.
Obsah kruhové výseče
Obsah kruhové výseče
Obsah kruhové výseče se středovým úhlem \alpha a poloměrem r spočítáme jako: \frac{\alpha}{360^{\circ}} \cdot \pi \cdot r^2
Příklady
- Kruhová výseč na obrázku má obsah: \frac{150^{\circ}}{360^{\circ}} \cdot \pi \cdot 3^2 = \frac{5}{12} \cdot \pi \cdot 9 = \frac{15}{4} \pi
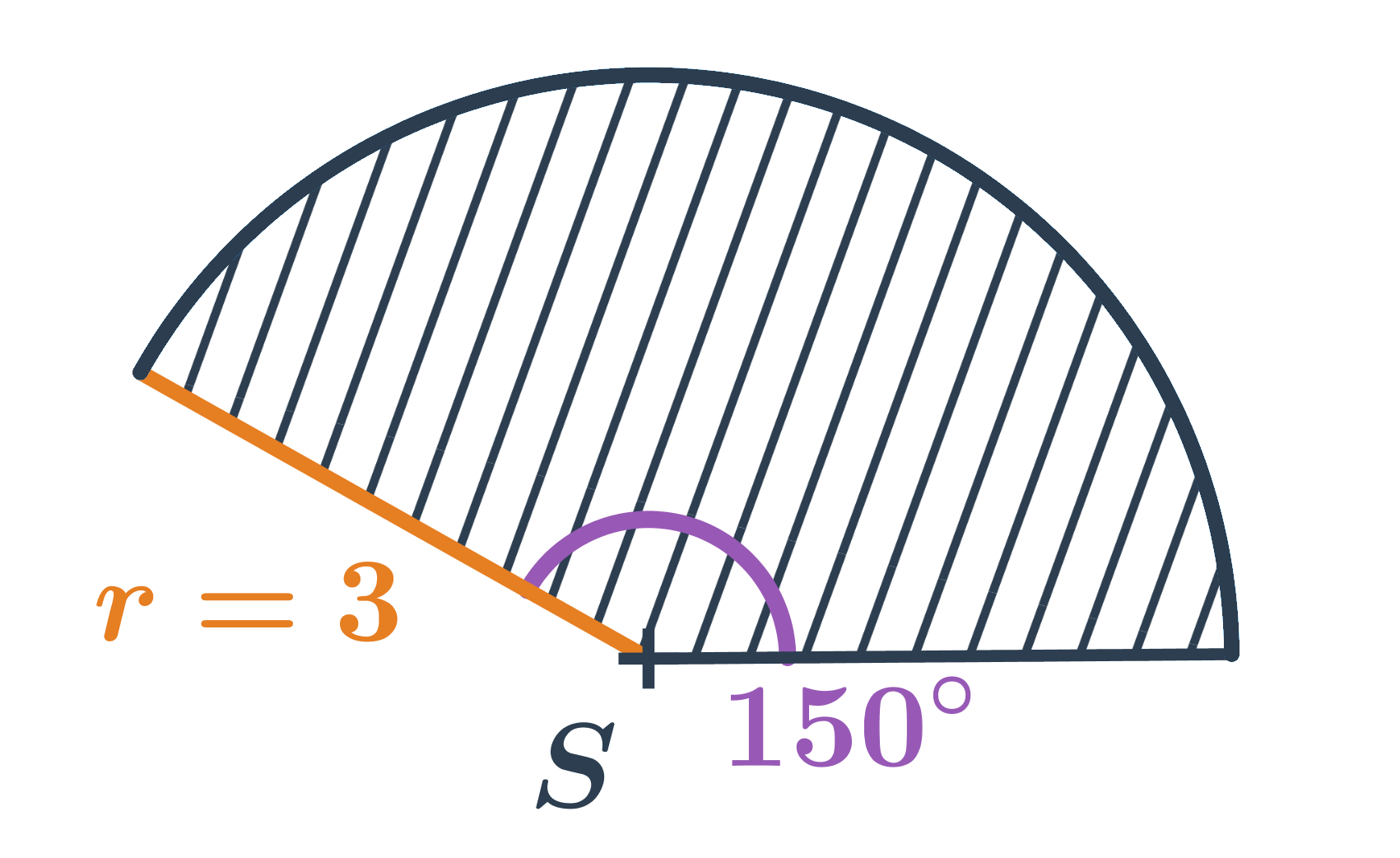
- Obsah celého kruhu (výseče se středovým úhlem 360^{\circ}) je: \frac{360^{\circ}}{360^{\circ}} \cdot \pi \cdot r^2 = \pi \cdot r^2
Délka oblouku
Délku oblouku, který na kružnici o poloměru r odpovídá středovému úhlu \alpha spočítáme jako: \frac{\alpha}{360^{\circ}} \cdot 2 \pi \cdot r
Příklad – délka oblouku odpovídajícího 90^{\circ}
Délka oblouku na obrázku je:
\frac{90^{\circ}}{360^{\circ}} \cdot 2\pi \cdot 3 = \frac{1}{4} \cdot 6 \pi = \frac{3}{2}\pi
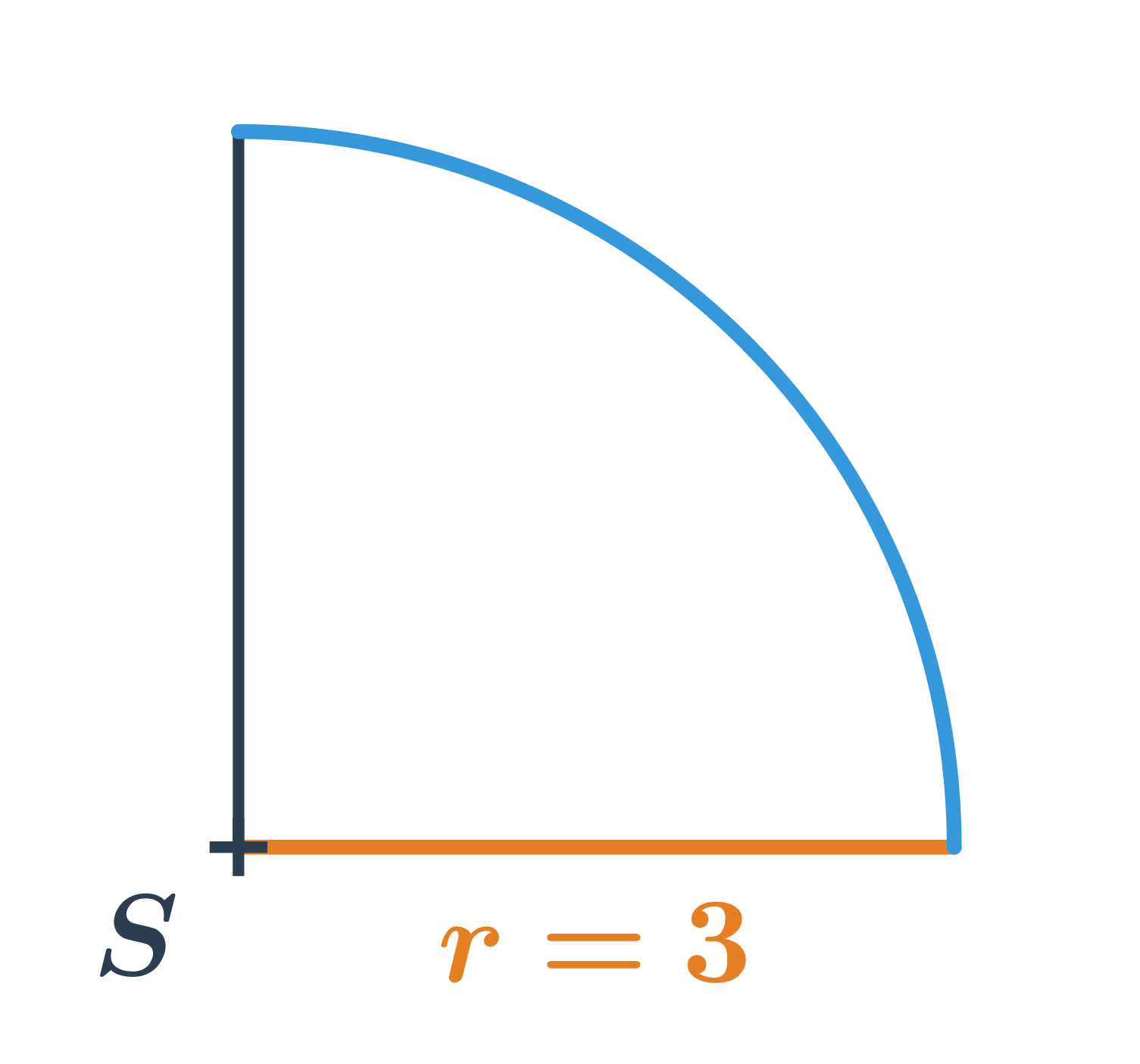 Jedná se o čtvrtinu délky kružnice.
Jedná se o čtvrtinu délky kružnice.
Příklad – délka oblouku odpovídajícího 360^{\circ}
Délka celé kružnice (tedy pro celých 360^{\circ}) je:
\frac{360^{\circ}}{360^{\circ}} \cdot 2\pi \cdot r = 2\pi \cdot r

