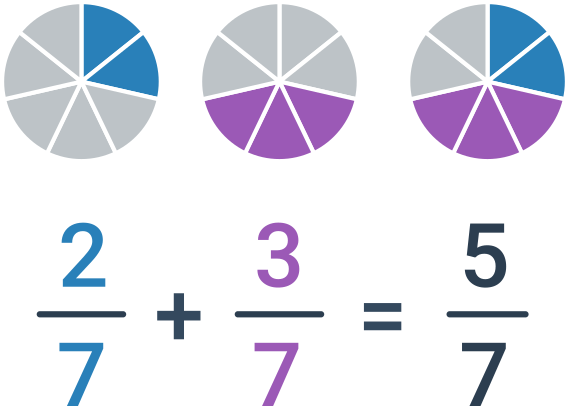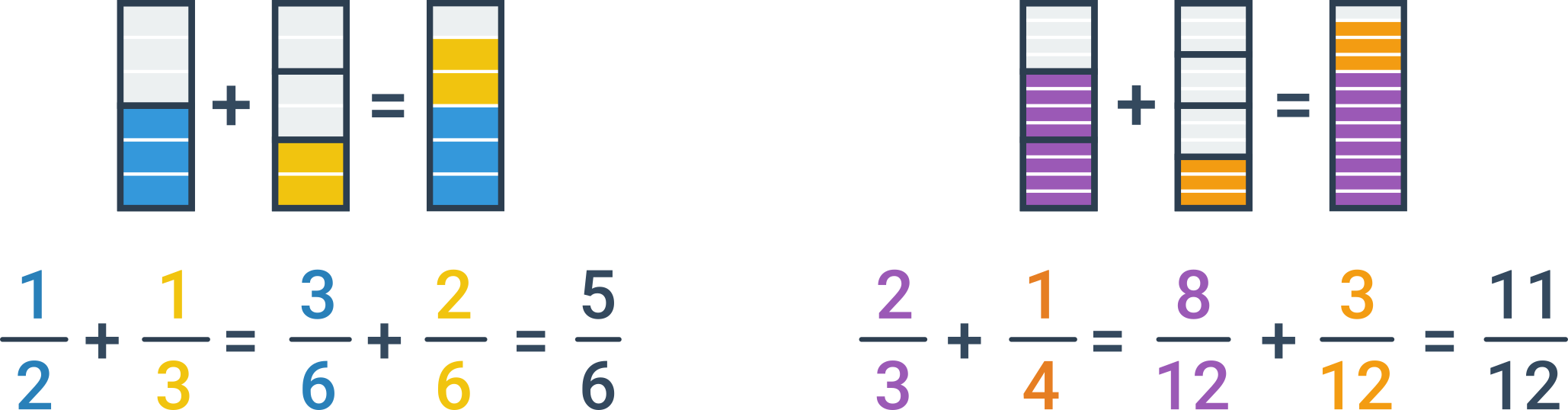Sčítání a odčítání zlomků

Než se pustíme do sčítání zlomků, je dobré mít jasno v tom, co je čitatel („to nahoře“) a jmenovatel („to dole“). Ve zlomku \frac{3}{7} je 3 čitatel, 7 jmenovatel.
Sčítání zlomků se stejným jmenovatelem
Pokud mají sčítané zlomky stejného jmenovatele, stačí prostě sečíst čitatele. Jmenovatele necháme stejného, tedy \frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}.
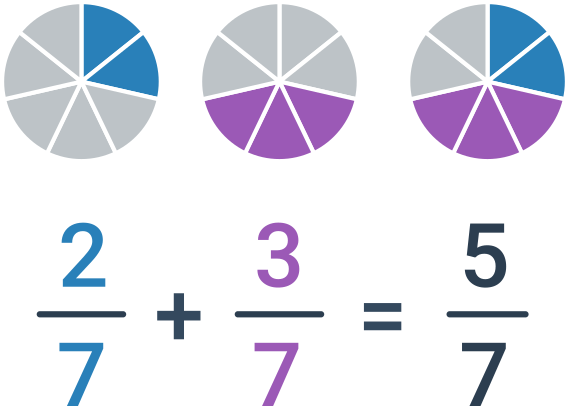
Sčítání zlomků s různými jmenovateli
Pokud mají sčítané zlomky různého jmenovatele, musíme je nejprve rozšířit tak, aby měly stejného jmenovatele. Nejvýhodnější je rozšířit zlomky na nejmenší společný násobek původních jmenovatelů. Jakmile mají zlomky stejného jmenovatele, sečteme je výše uvedeným postupem.
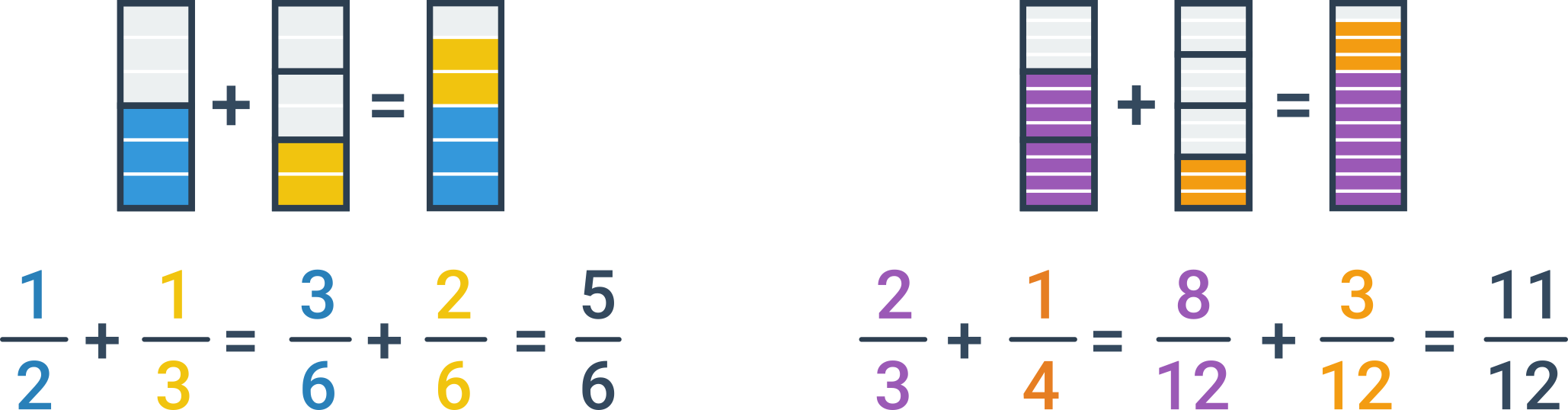
Úpravy a odčítání
Výsledný zlomek většinou ještě krátíme, abychom dostali výsledek v základním tvaru. Odčítání zlomků funguje stejným způsobem.
Příklady
Příklady se stejným jmenovatelem, bez nutnosti krácení
\frac{2}{5} + \frac{1}{5} = \frac{2+1}{5} = \frac{3}{5}
\frac{5}{7} - \frac{2}{7} = \frac{5-2}{7} = \frac{3}{7}
Příklady se stejným jmenovatelem, kdy výsledek krátíme
\frac{5}{6}-\frac{1}{6} = \frac{5-1}{6} = \frac{4}{6} = \frac{2}{3}
\frac{8}{9} - \frac{2}{9} = \frac{8-2}{9} = \frac{6}{9} = \frac{2}{3}
Příklad s různými jmenovateli: \frac{5}{6} - \frac{3}{4}
- Nejmenší společný násobek jmenovatelů 6 a 4 je 12, rozšíříme tedy zlomky na jmenovatele 12.
- \frac{5}{6} - \frac{3}{4} = \frac{5\cdot 2}{6\cdot 2} - \frac{3\cdot 3}{4\cdot 3}= \frac{10}{12} - \frac{9}{12} = \frac{1}{12}
Příklady s různými jmenovateli: \frac{7}{8} + \frac{2}{5}
- Nejmenší společný násobek jmenovatelů 8 a 5 je 40, rozšíříme tedy zlomky na jmenovatele 40.
- \frac{7}{8} + \frac{2}{5} = \frac{7 \cdot 5}{8 \cdot 5} + \frac{2 \cdot 8}{5 \cdot 8} = \frac{35}{40} + \frac{16}{40} = \frac{51}{40}
Pracovní list
Kromě interaktivního procvičování je k dispozici také pracovní list pro tisk:
Komiks pro zpestření
Zavřít