
Osová souměrnost

Osová souměrnost je dána přímkou o a přiřazuje každému bodu X mimo osu takový bod X', že přímka o je osou úsečky XX'. Jinými slovy: obraz má od osy stejnou vzdálenost jako původní bod a spojnice bodů je kolmá na osu. Osová souměrnost zachovává vzdálenosti i úhly, jde tedy o druh shodnosti.
Příklady
Modré a oranžové útvary jsou vzájemně osově souměrné podle osy o:
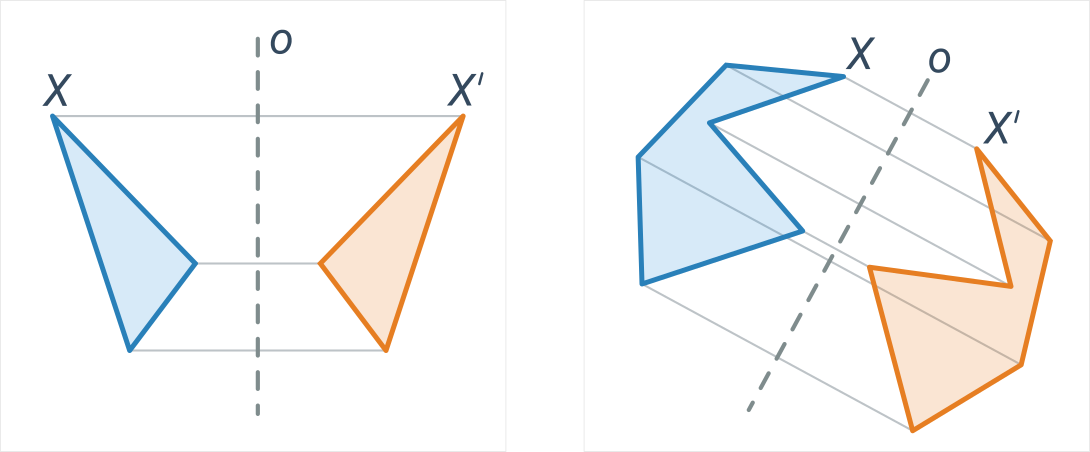
Pro lepší pochopení může být užitečné porovnat osovou a středovou souměrnost.
Osově souměrný útvar
Útvar označujeme za osově souměrný, pokud je v nějaké osové souměrnosti obrazem sebe sama. Osu této souměrnosti pak nazýváme osou útvaru. Obrázek uvádí příklady útvarů osově souměrných (zelené, s vyznačenými osami souměrnosti) i těch nesouměrných (červené):
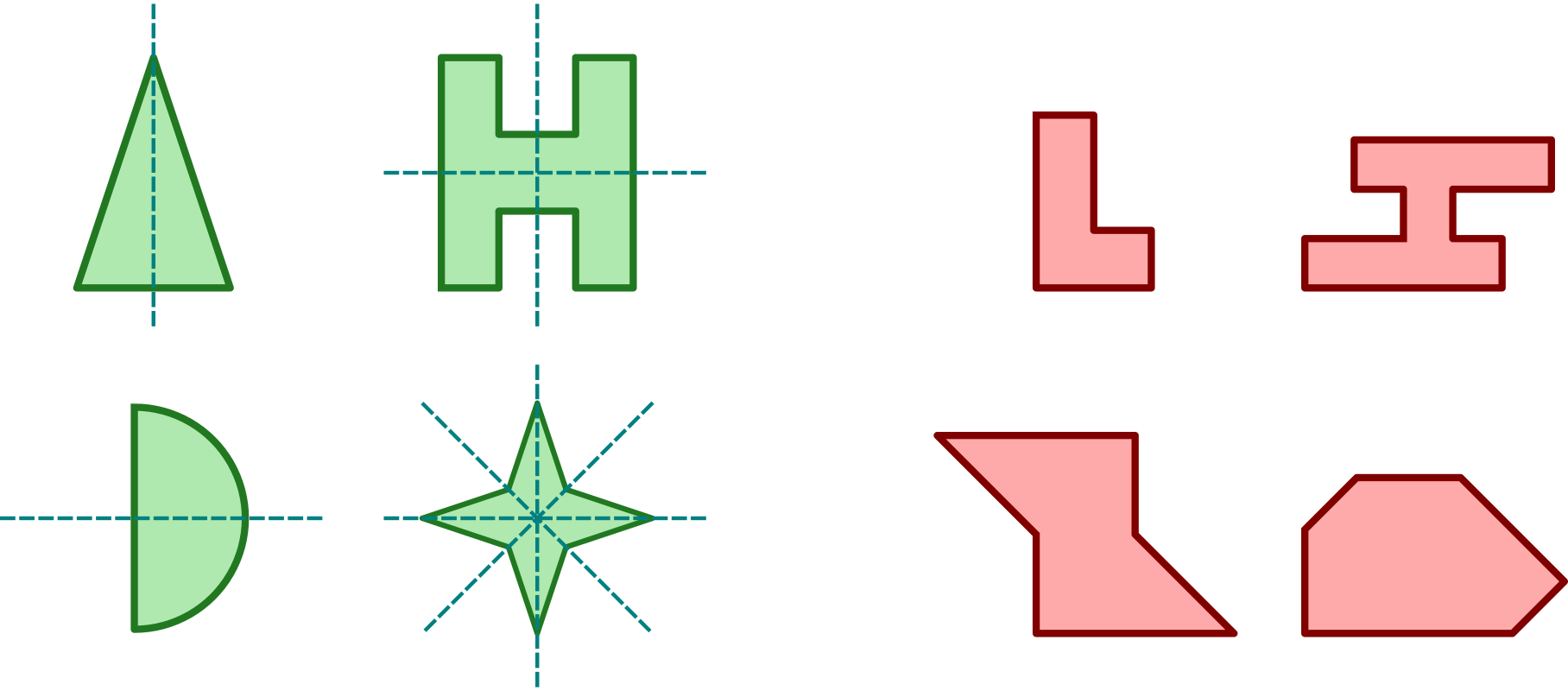
Další příklady:
- Úsečka je osově souměrná a má v rovině jedinou osu souměrnosti (kolmici v jejím středu).
- Rovnoramenný trojúhelník je osově souměrný.
- Trojúhelník, který není rovnoramenný, není osově souměrný.
- Všechny pravidelné mnohoúhelníky jsou osově souměrné. Počet os souměrnosti je roven počtu vrcholů mnohoúhelníku.
- Kruh je osově souměrný a má nekonečně mnoho os souměrnosti.
Komiks pro zpestření
Zavřít














