Výpis souhrnů
Násobení a dělení
Podtémata
Násobení a dělení
Násobení a dělení jsou základní početní operace, které navazují na sčítání a odčítání.
Násobení a dělení malými čísly se vyplatí umět důkladně zpaměti. Je to něco jako znalost základních slovíček v cizím jazyce. Bez hladkého zvládnutí základních výpočtů se v matematice „nedomluvíme“.
Na tyto základy navazuje násobení a dělení vícecifernými čísly. Na tom si dobře procvičíme základní násobilku a důkladné pochopení principu násobení a dělení:
Pro větší čísla pak používáme písemný zápis:
Téma násobení, dělení a logické myšlení pak představuje různé zajímavé logické úlohy, u kterých je potřeba nejen dobře počítat, ale také promyslet správný postup řešení.
Výukové moduly
Konkrétní náměty, jakým způsobem učivo procvičovat a v jakém pořadí, poskytují výukové moduly:
| 2.–4. ročník | násobení a dělení v rozsahu malé násobilky (jednociferní činitelé), důraz na pamětné počítání | |
| 4.–6. ročník | počítání s vícecifernými čísly, písemné postupy, slovní úlohy |
Malá násobilka
Násobení nám říká, kolik čtverečků má čokoláda, když víme, kolik má řádků a sloupců:
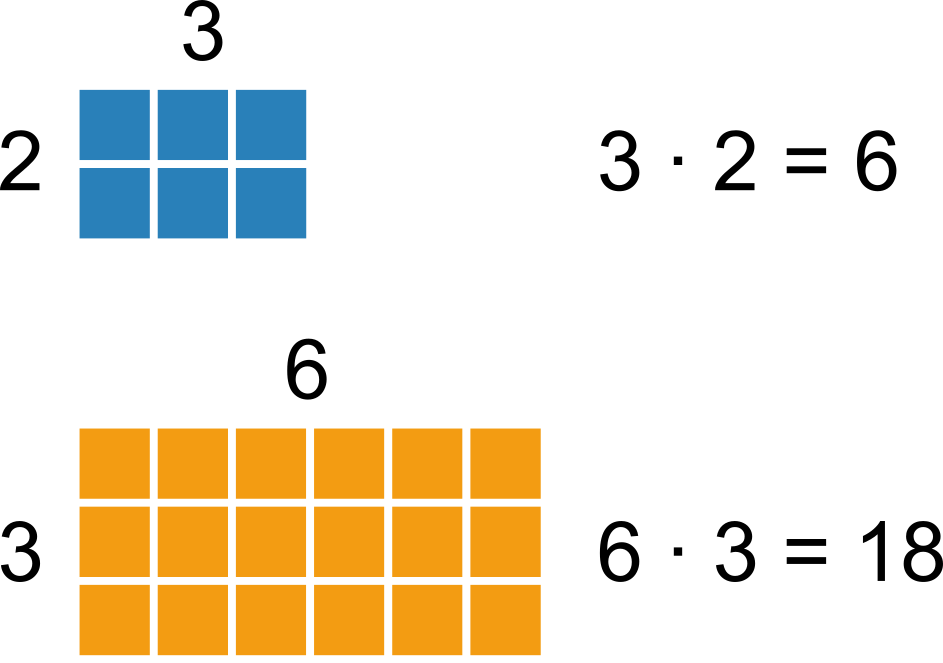
Násobení využíváme v matematice i v běžném životě velice často. Proto se velmi vyplatí naučit se základní násobky zpaměti.
Malá násobilka zahrnuje vzájemné součiny čísel od 1 do 10. Ty můžeme přehledně vyjádřit tabulkou malé násobilky:
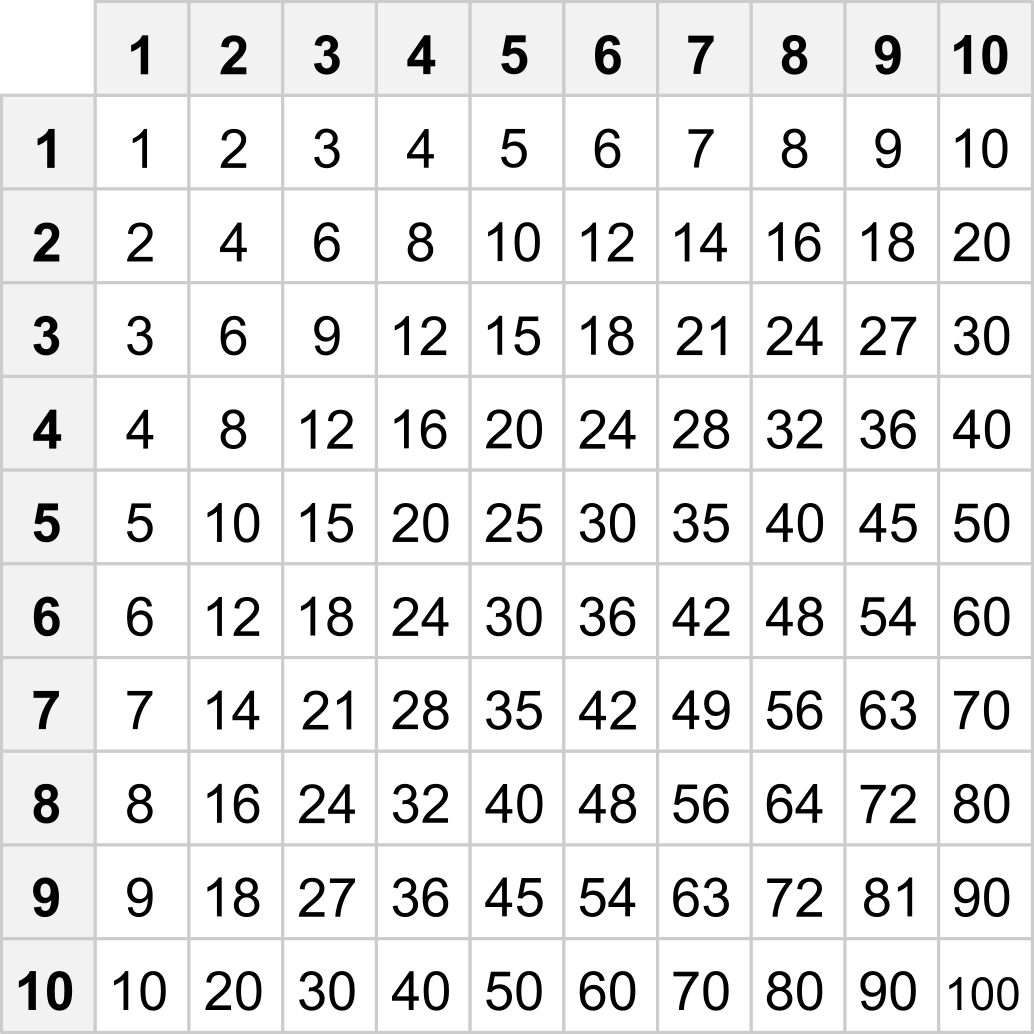
Můžete si procvičit zvlášť Násobilku čísla 2, Násobilku čísla 3, Násobilku čísla 4, Násobilku čísla 5, Násobilku čísla 6, Násobilku čísla 7, Násobilku čísla 8, Násobilku čísla 9 a Násobilku čísla 10.
Pracovní list: slovní úlohy
Kromě interaktivních cvičení je k dispozici také pracovní list na vytištění:
Komiks pro zpestření
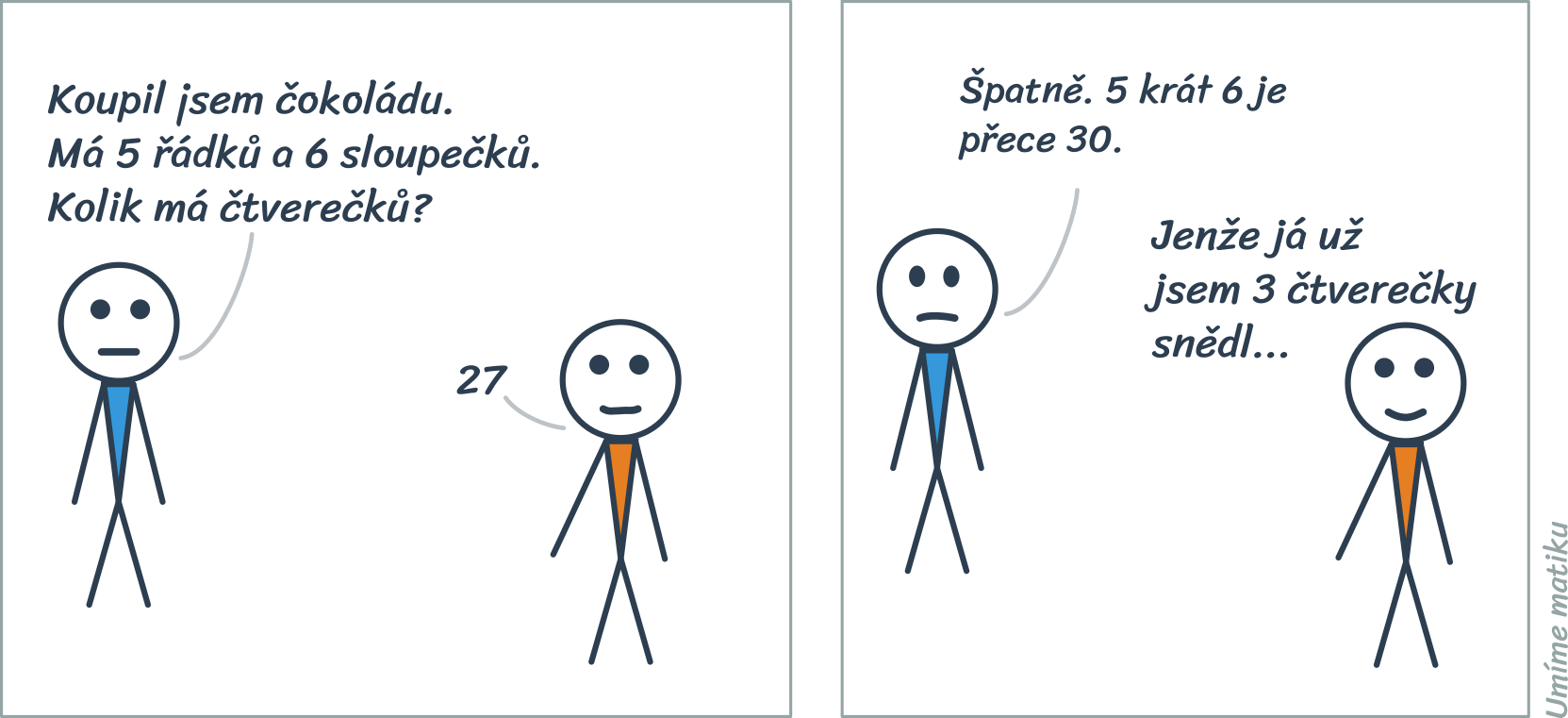
Dělení jednociferné
Když mám 8 jablíček a chci je rozdělit rovnoměrně do 4 košíků, kolik jablíček bude v každém košíku? Této otázce v matematice odpovídá dělení:
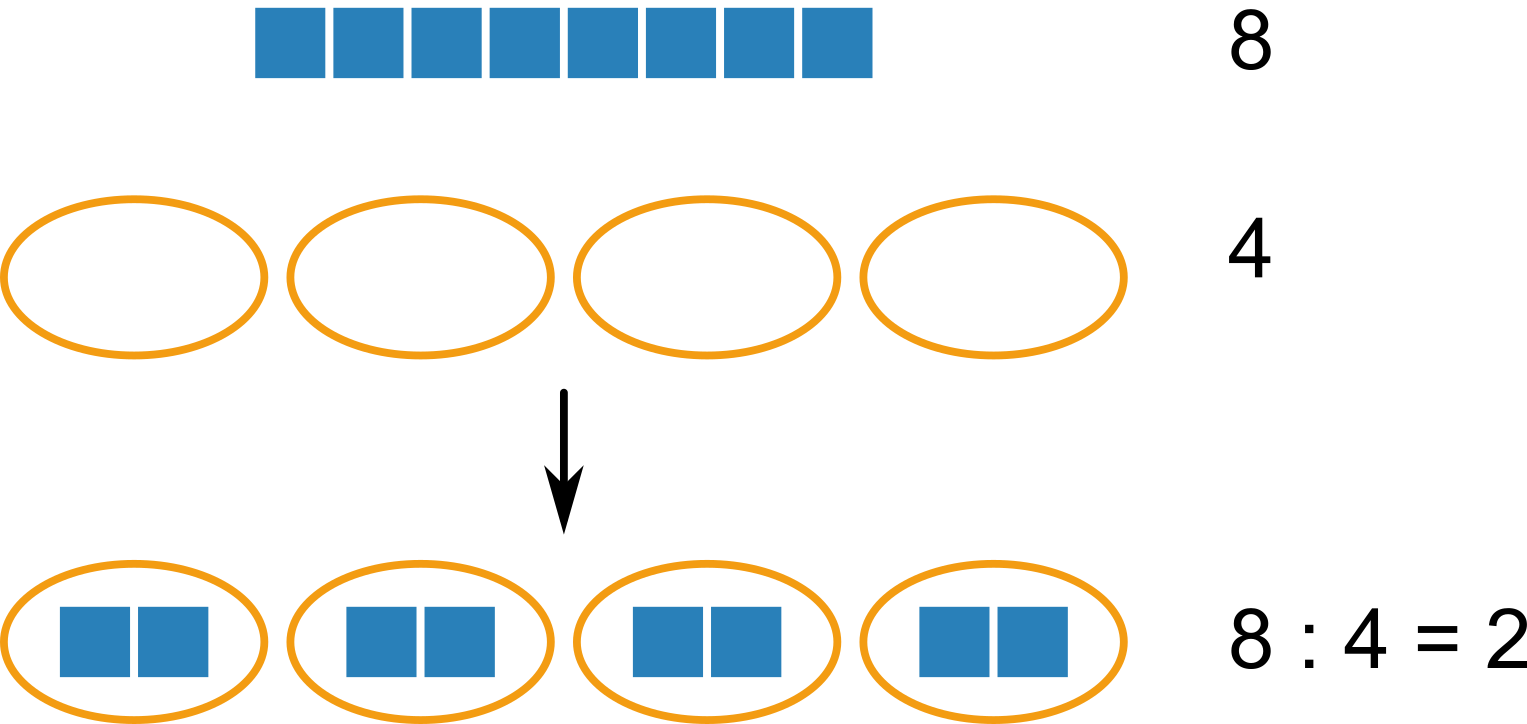
Dělení se zbytkem
Zbytek po dělení je početní operace související s celočíselným dělením. Pokud dělíme a:b, pak můžeme psát a = k\cdot b + z, přičemž 0 \leq z \lt b. Číslo k nazýváme podíl, číslo z zbytek. Operace dělení se zbytkem se v matematice nazývá též modulo.
Příklad: 11:4 dává podíl 2 a zbytek 3, protože 11 = 2\cdot 4 + 3. Pokud mám 11 jablek a rozdělím je rovnoměrně do 4 košíků, v každém košíku budou 2 jablka a ještě mi 3 zbydou.
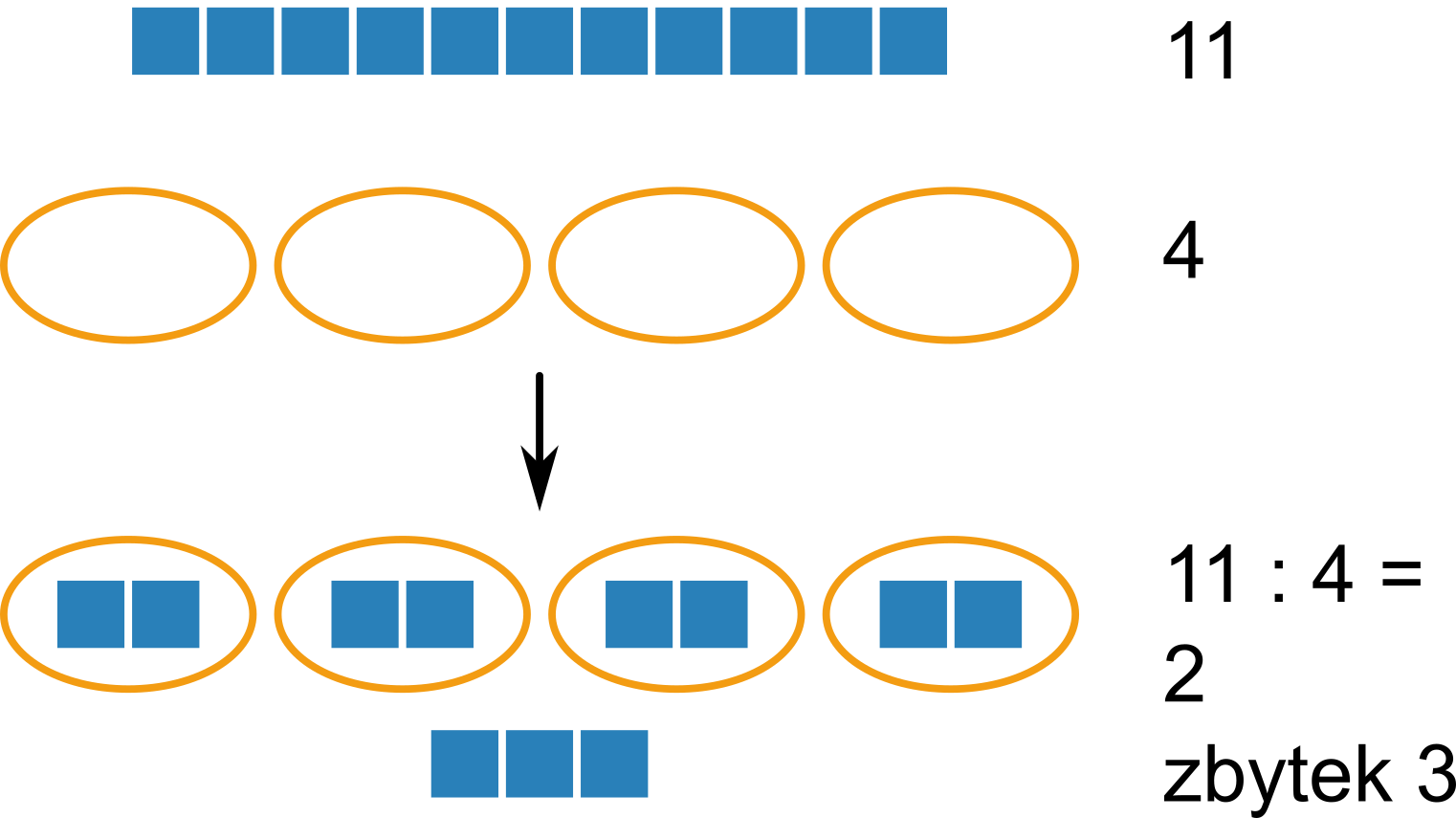
Další příklady:
- 17:5 dává zbytek 2, protože 17 = 3\cdot 5 + 2.
- 21:6 dává zbytek 3, protože 21 = 3\cdot 6 + 3.
- 12:7 dává zbytek 5, protože 12 = 1\cdot 7 + 5.
- 4:6 dává zbytek 4, protože 4 = 0\cdot 6 + 4.
Komiks pro zpestření
Písemné násobení pod sebou
Při písemném násobení postupujeme následovně:
- Čísla si napíšeme pod sebe, zarovnaná doprava.
- Postupně jednotlivými ciframi spodního čísla pronásobíme celé horní číslo.
- Výsledky dílčích násobení zapisujeme na řádky pod sebe. Výsledky odsazujeme podle pozice cifry, kterou jsme násobili.
- Nakonec všechny dílčí výsledky sečteme (viz postup pro sčítání pod sebou).
Obrázek ukazuje příklad násobení čísel 79 a 68.

Násobení, dělení a logické myšlení
Zde jsou zajímavé úlohy, na kterých si můžete zábavnou formou procvičit operace násobení a dělení a také svou schopnost logicky přemýšlet a naplánovat si správný postup.
Nahoru
