
Jehlan

Jehlan je prostorový geometrický útvar, který má jednu podstavu a plášť tvořený trojúhelníky. Podstava jehlanu může být libovolný mnohoúhelník (například čtverec, obdélník nebo trojúhelník) a všechny boční stěny (plášť) se setkávají v jednom společném bodě nazývaném vrchol jehlanu. Příkladem jehlanů jsou pyramidy ze starověkého Egypta, vypadají zhruba jako jehlany se čtvercovou podstavou a čtyřmi trojúhelníkovými bočními stěnami.
Vzorce pro objem a povrch
Objem jehlanu V = \frac{1}{3} S_p \cdot v, kde S_p je obsah podstavy a v je výška jehlanu, což je vzdálenost vrcholu od roviny podstavy. (Velikost výšky jehlanu získáme jako délku úsečky, která vede od vrcholu k rovině podstavy a je kolmá na tuto rovinu.)
Povrch jehlanu získáme jako součet obsahu podstavy S_p a obsahu pláště S_{pl} (obsah pláště je roven součtu obsahů všech bočních trojúhelníkových stěn jehlanu). Celkově je povrch jehlanu S = S_p + S_{pl}, v případě pravidelného šestibokého jehlanu na obrázku je: S=Sp + 6 \cdot S_{\Delta}
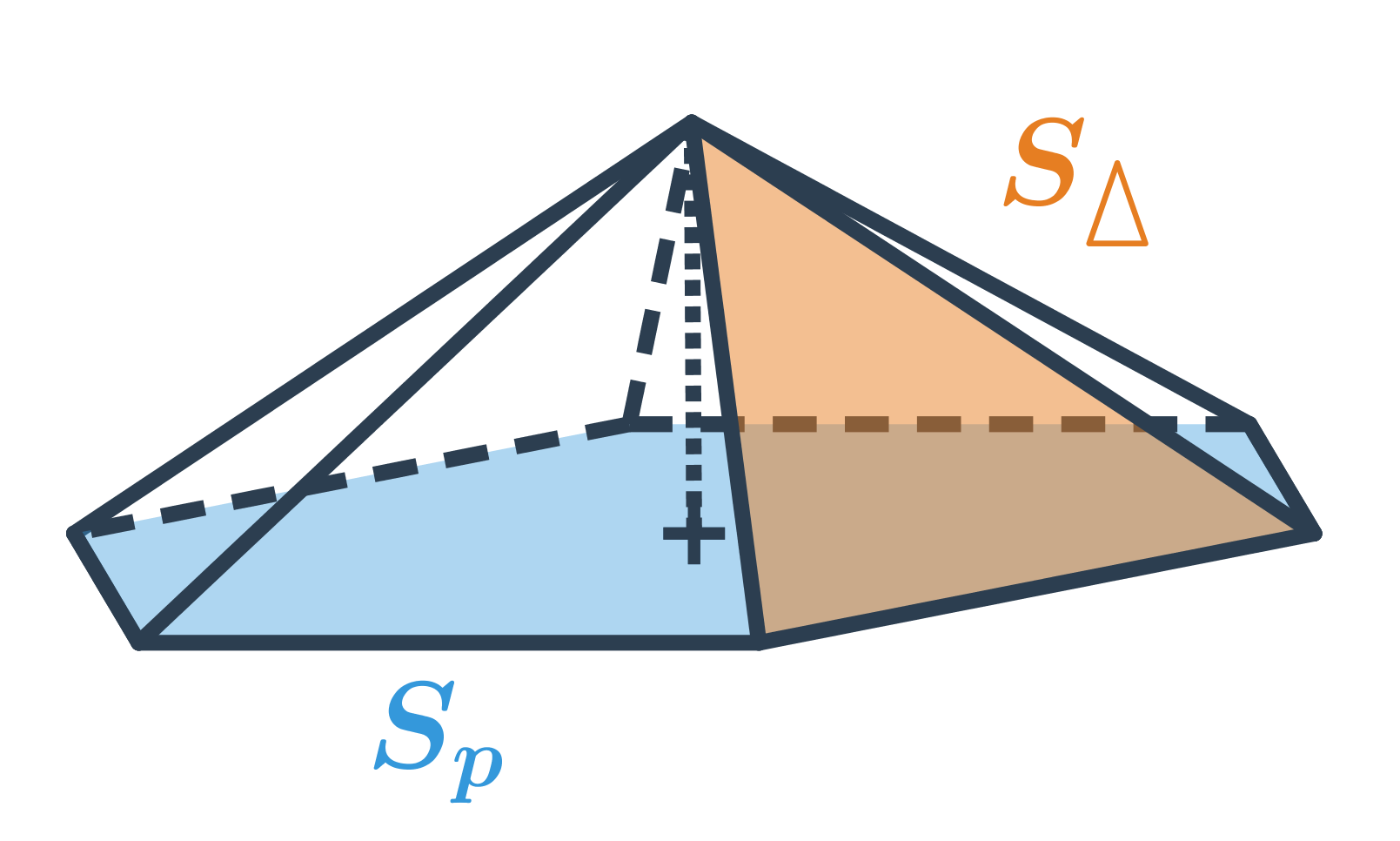
Některé jehlany mají pravidelnou podstavu, vrchol umístěný přímo nad středem podstavy a všechny trojúhelníkové stěny z pláště stejné, ale obecně se může výpočet obsahu každé z těchto trojúhelníkových stěn lišit v závislosti na tvaru podstavy jehlanu.
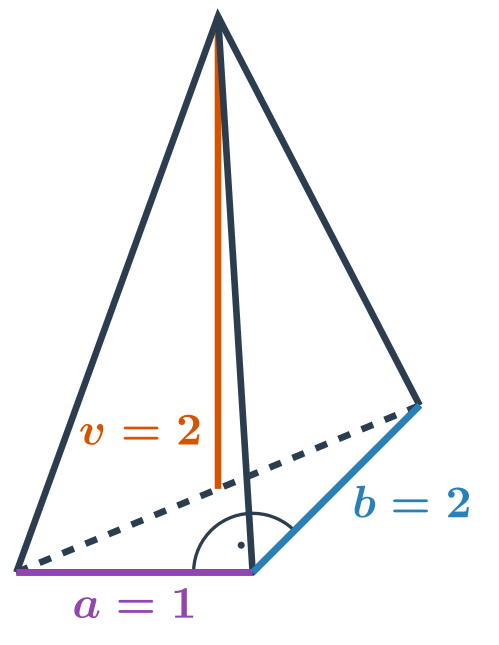
Speciální případy
Pravidelný čtyřstěn je jehlan, jehož základna i všechny tři boční stěny jsou rovnostranné trojúhelníky. Je jedním z Platónských těles.
Pokud máme pravidelný čtyřstěn, jehož stěny jsou rovnostranné trojúhelníky s délkou každé strany a, umíme si pomocí Pythagorovy věty spočítat výšku každého z těchto rovnostranných trojúhelníků \frac{\sqrt{3}}{2} a.
Povrch pravidelného čtyřstěnu
- Obsah podstavy pravidelného čtyřstěnu se stranou délky a je obsah jednoho ze čtyř stejných rovnostranných trojúhelníků: S_p = \frac{1}{2} \cdot a \cdot \frac{\sqrt{3}}{2} a = \frac{\sqrt{3}}{4} a^2.
- Povrch pravidelného čtyřstěnu se stranou délky a je: 4 \cdot S_p = \sqrt{3} \cdot a^2
Objem pravidelného čtyřstěnu
- V rovnostranném trojúhelníku leží těžnice na výškách a zároveň na osách vnitřních úhlů. Vrchol pravidelného čtyřstěnu leží na přímce, která je kolmá k jeho podstavě a protíná ji v ortocentru (což je zároveň také těžiště rovnostranného trojúhelníka).
- Můžeme tedy spočítat pomocí Pythagorovy věty nejen výšku trojúhelníků, které tvoří stěny pravidelného čtyřstěnu, ale také výšku celého tělesa:
- v^2 = a^2 - (\frac{2}{3} \cdot \frac{\sqrt{3}}{2} a )^2 = (1-\frac{1}{\sqrt{3}})\cdot a^2
- v = \sqrt{(1-\frac{1}{\sqrt{3}})}\cdot a
- Objem pravidelného čtyřstěnu se stranou délky a je:
- \frac{1}{3} S_p \cdot v = \frac{1}{3}\cdot \frac{\sqrt{3}}{4} a^2 \cdot \sqrt{(1-\frac{1}{\sqrt{3}})}\cdot a = \frac{1}{4\cdot \sqrt{3}}\cdot \sqrt{(1-\frac{1}{\sqrt{3}})}\cdot a^3
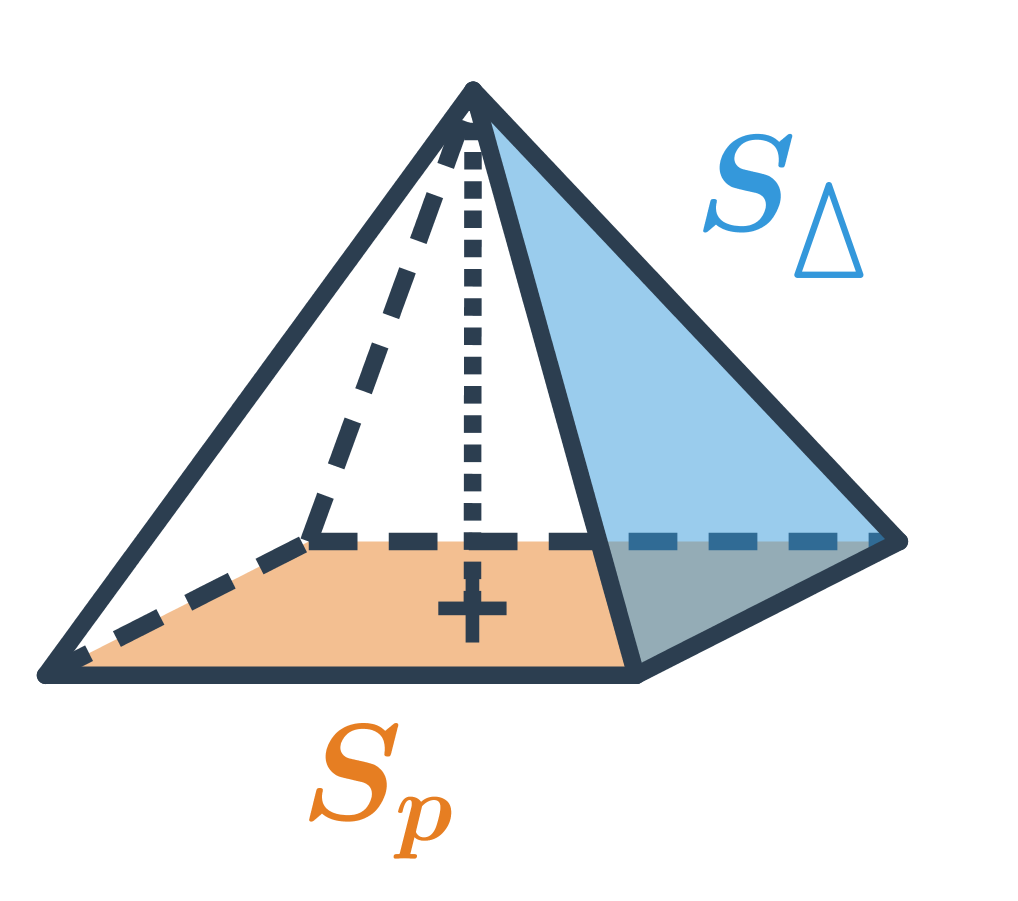
Pravidelný n-boký jehlan má jako podstavu pravidelný n-úhelník, jeho plášť tvoří n rovnoramenných trojúhelníků. Například podstava pravidelného čtyřbokého jehlanu je čtverec, jeho plášť tvoří čtyři rovnoramenné trojúhelníky.
Zavřít












