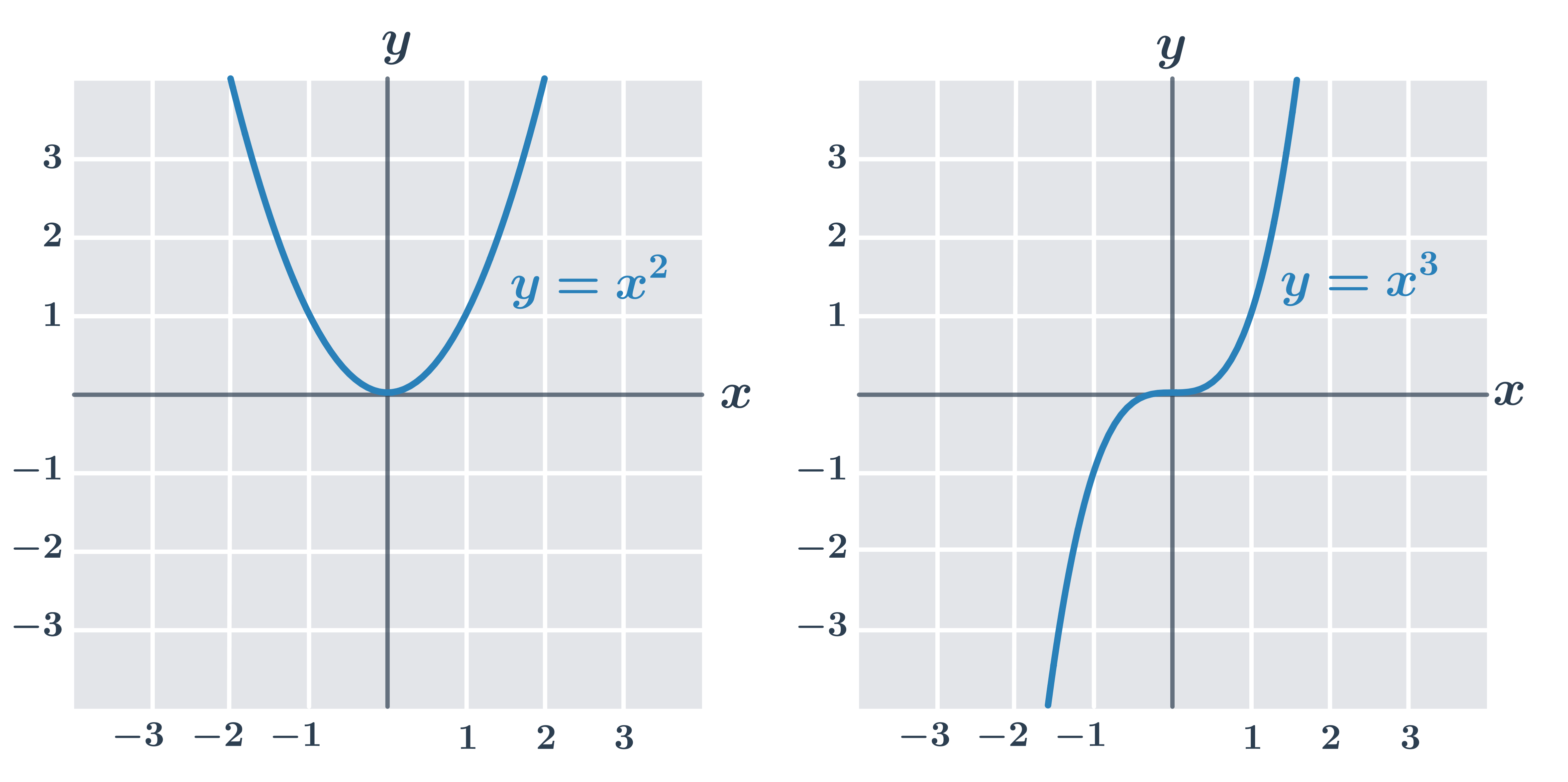Čeština
Angličtina
Informatika
Biologie
Němčina
Umíme to
Zeměpis
Chemie
Dějepis
Fyzika
ZSV
Aritmetika
Zlomky, procenta, desetinná čísla
Geometrie
Elementární algebra
Funkce
Jednotky, míry
Diskrétní matematika
Finanční gramotnost
Rozhodovačka
Pexeso
Krok po kroku
Psaná odpověď
Grafař
Porozumění
Označování
Přesouvání
Mřížkovaná
Rozdělovačka
Rozbitá kalkulačka
Roboti
Střílečka
Příšerky
Závody
Územíčka
Tipovačka
Týmovka
Můj účet
Odhlásit se
Rozhodovačka
Grafy mocninných funkcí
Procvičujte neomezeněVáš denní počet odpovědí je omezen. Pro navýšení limitu či přístup do svého účtu s licencí se přihlaste.
Přihlásit se
G42
QR kód
Kód / krátká adresa
Zkopírujte kliknutím.
Nastavení cvičení
Pozor, nastavení je platné pouze pro toto cvičení a předmět.
Grafy mocninných funkcí
Grafy základních mocninných funkcí y= x^n
pro n sudé – graf je souměrný podle osy y, D(f)=\R, H(f)=\langle0, \infty)
pro n liché – graf je souměrný podle počátku, D(f)=\R, H(f)=\R
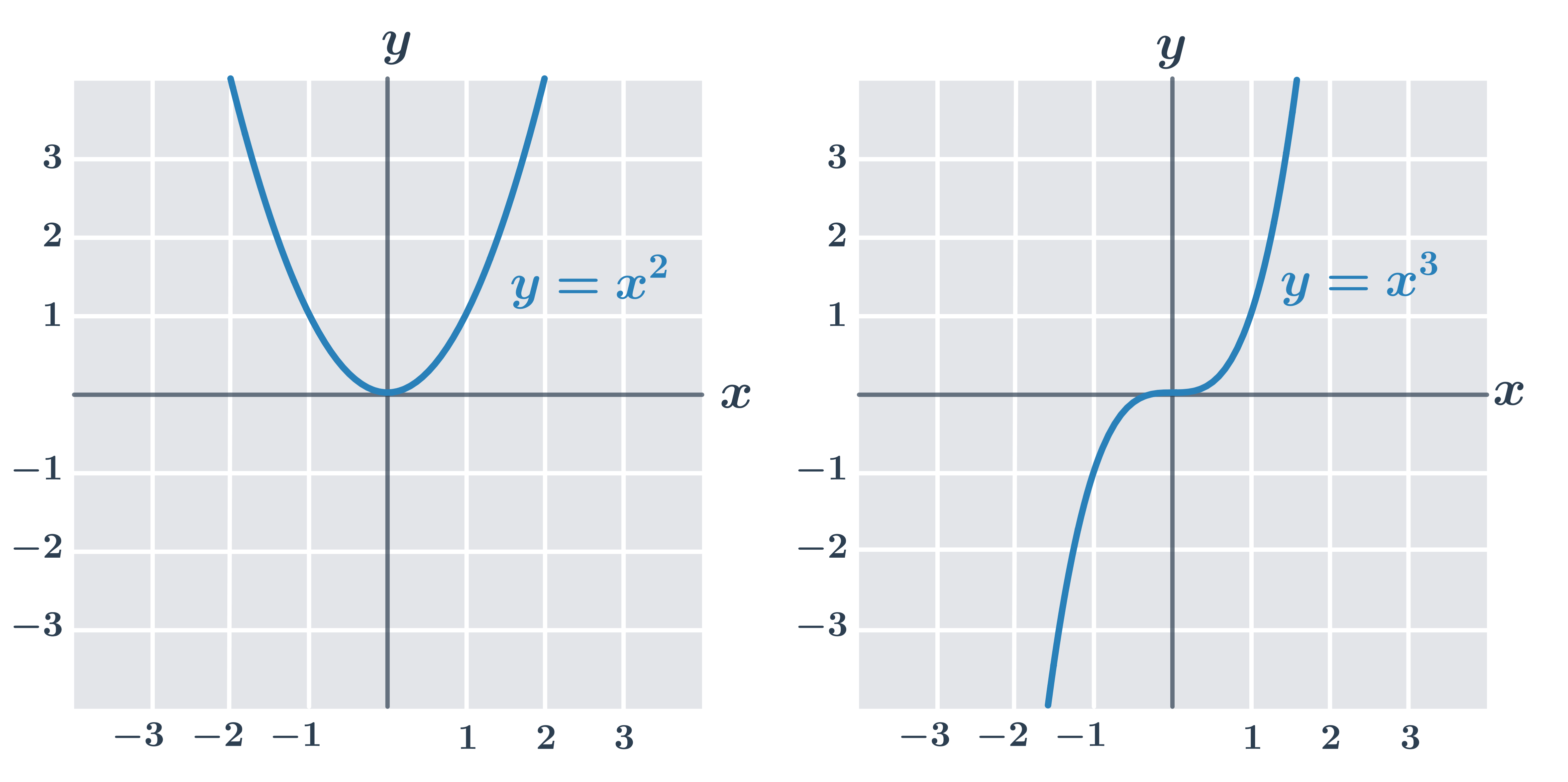
Grafy mocninných funkcí se záporným exponentem y= x^{-n}
pro n sudé – graf souměrný podle osy y, D(f)=\R- \{0\}, H(f)=\langle0, \infty)
pro n liché – graf souměrný podle počátku, D(f)=\R - \{0\}, H(f)=\R - \{0\}
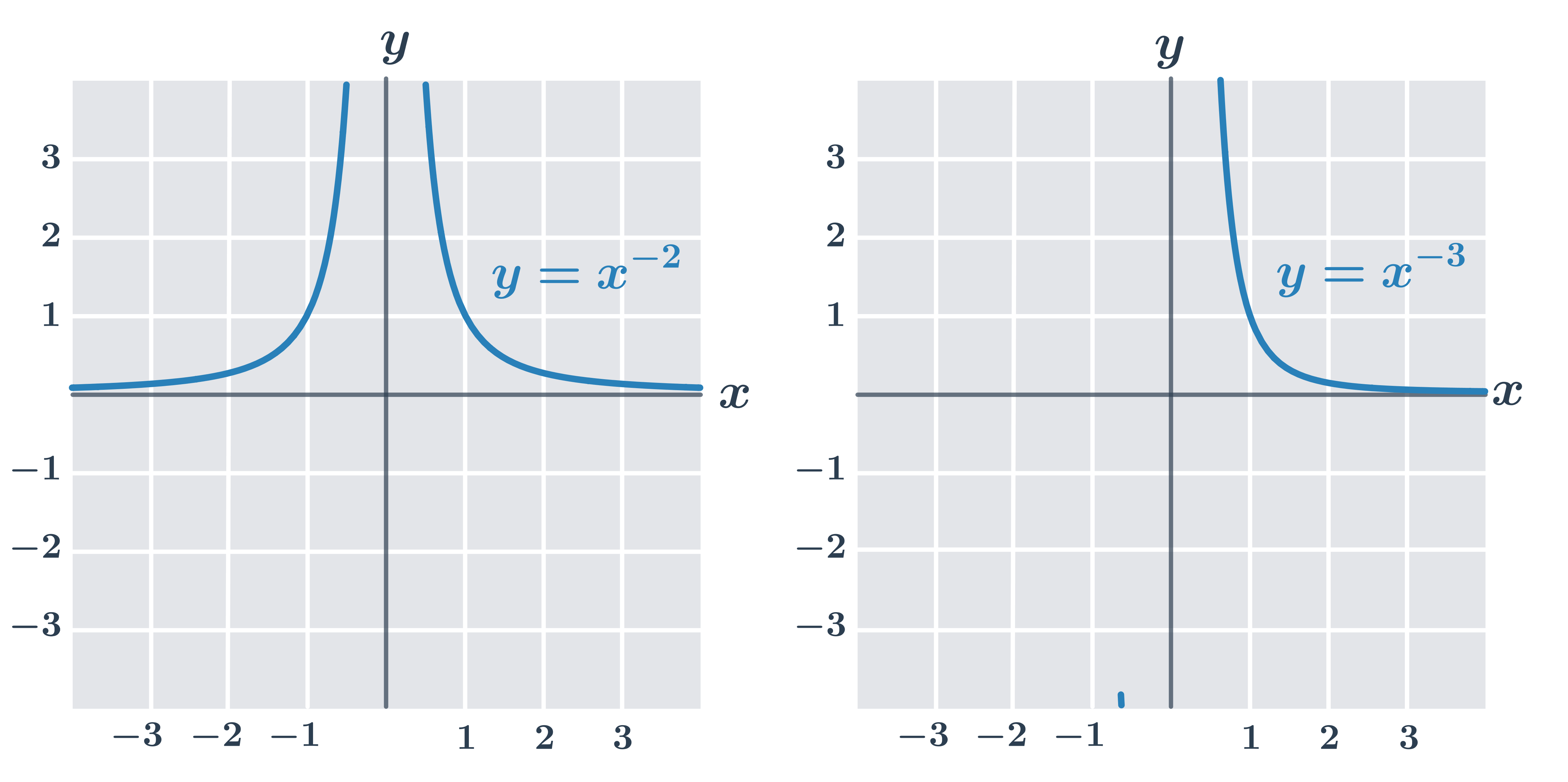
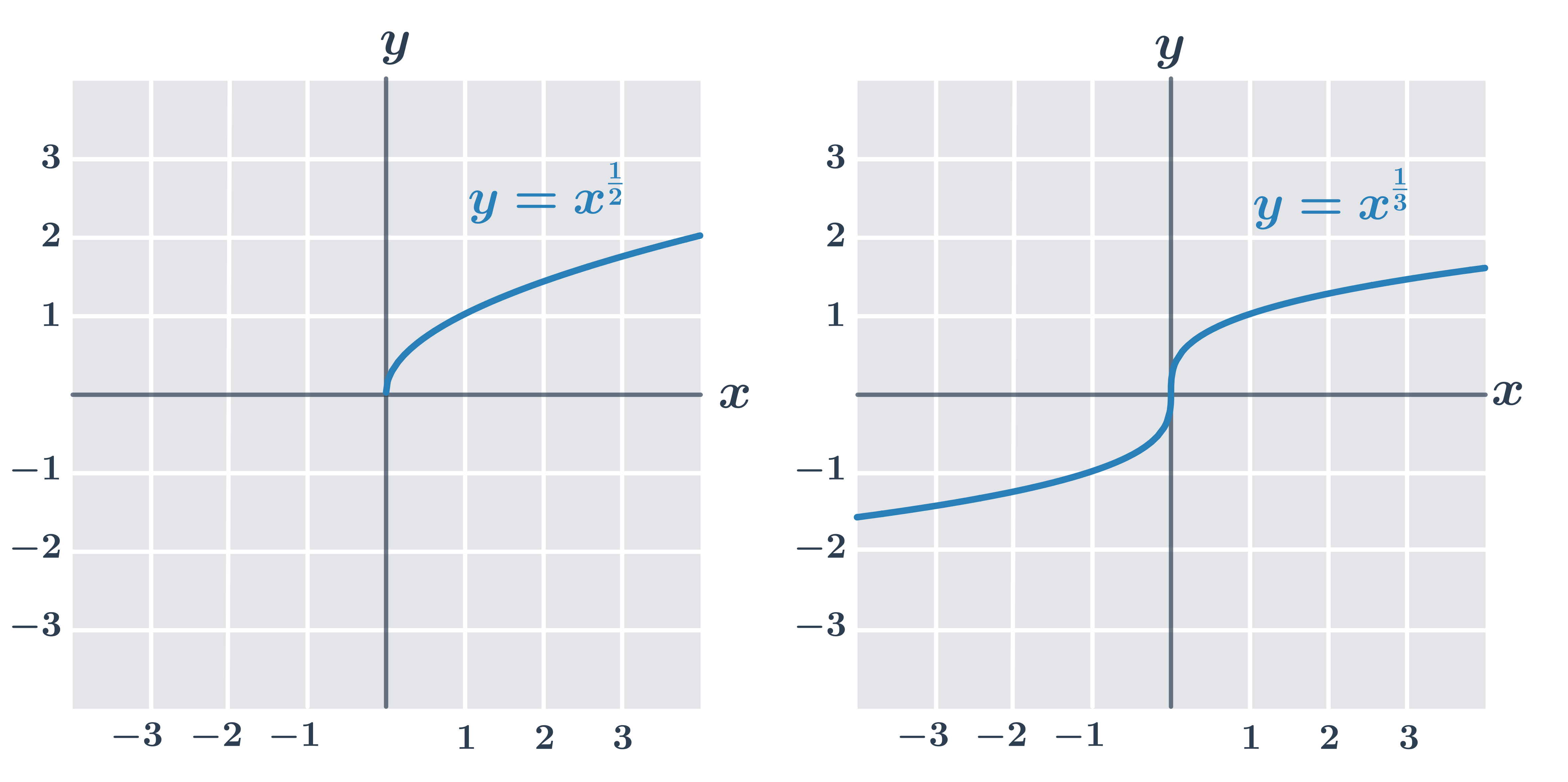
Grafy funkcí y= x^{\frac{1}{n}}:
pro sudé n – funkce y= x^{\frac{1}{n}} definováno na kladných číslech, D(f)=\langle0, \infty), H(f)=\langle0, \infty)
pro liché n – funkce y=x^n je prostá, proto bychom mohli definovat n.tou odmocninu i pro záporná čísla, ale často se (např. jako příprava pro práci s mocninnými funkcemi s obecnějšími racionálními exponenty) všechny n.té odmocniny pro sudá i lichá n definují pro jednoduchost jen na intervalu [0,\infty).
Poznámka: výpočty s mocninami a odmocninami
Při výpočtech s mocninami a odmocninami musíme být obezřetní, hodně pravidel platí pro nezáporný základ (pokud počítáme s odmocninami), případně kladný základ (nulu můžeme odmocňovat, ale nesmíme dělit nulou). Příklady:
součin odmocnin je odmocnina součinu: pro nezáporná čísla jako základy odmocnin pravidlo platí, pokud bychom chtěli použít pro záporný základ, nemusí nám v oboru reálných čísel vycházet smysluplné věci: \sqrt{-2} není definovaná, ale \sqrt{(-2)\cdot(-2)} je \sqrt{4} = 2
racionální exponenty: mělo by x^{\frac{2}{6}} být totéž jako x^{\frac{1}{3}}? Exponent je „stejné racionální číslo“, ale pro záporná x by vycházely u těchto dvou předpisů jiné funkční hodnoty (6. odmocnina ze záporného x není definovaná, 6. odmocnina z druhé mocniny záporného čísla je kladná, a 3. odmocnina z x by pro záporná x byla záporná).
racionální exponenty konkrétněji: čemu by se mělo rovnat (-8)^{\frac{2}{6}}? Máme (-8)^{\frac{1}{3}}=-2, ale zároveň \sqrt[6]{(-8)^2} = \sqrt[6]{64} = 2. Můžeme se dostat do potíží, když budeme pravidla, která platí pro mocniny a odmocniny kladných a nezáporných čísel, zkoušet používat i pro záporné základy.
Vliv úprav funkčního předpisu na graf mocninné funkce
Obrázek ukazuje několik úprav funkce y= x^3:
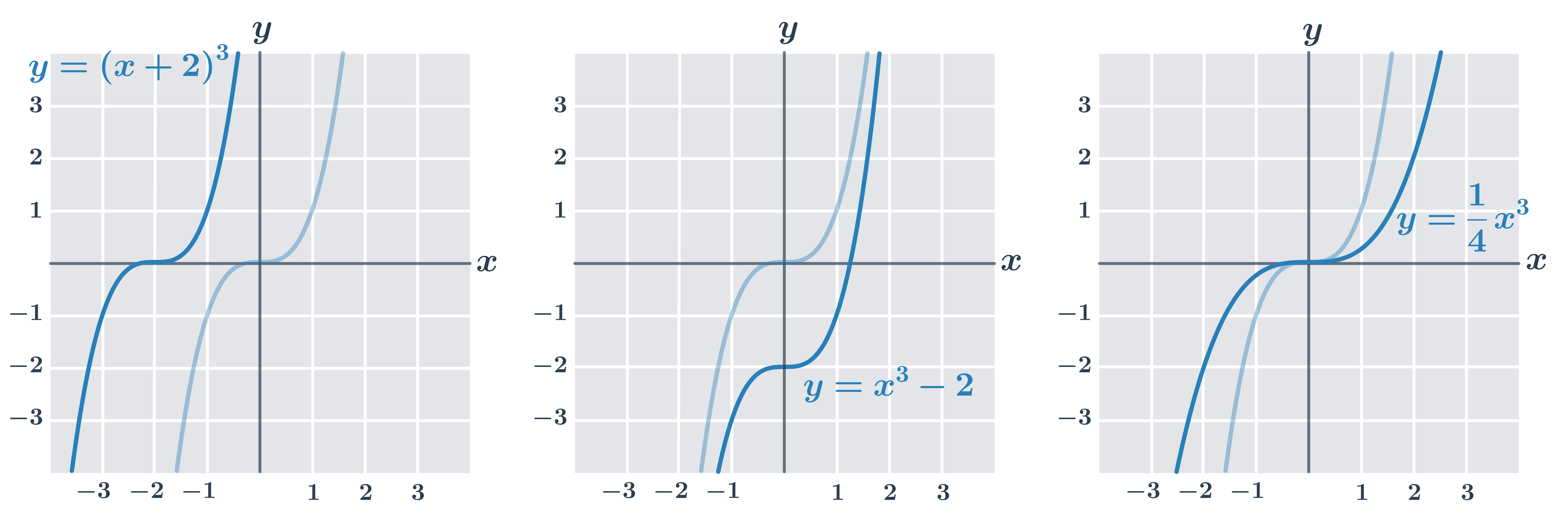
| y= (x+2)^3 | graf je posunutý ve směru osy x |
| y=x^3-2 | graf je posunutý ve směru osy y |
| y=\frac{1}{4} x^3 | graf bude natažený nebo smrštěný ve směru osy y (v uvedeném grafu se funkční hodnoty zmenší na čtvrtinu, například pro x=2 je hodnota funkce y=\frac{1}{4} \cdot 2^3=2) |
Grafy mocninných funkcí (střední)
Vyřešeno:
