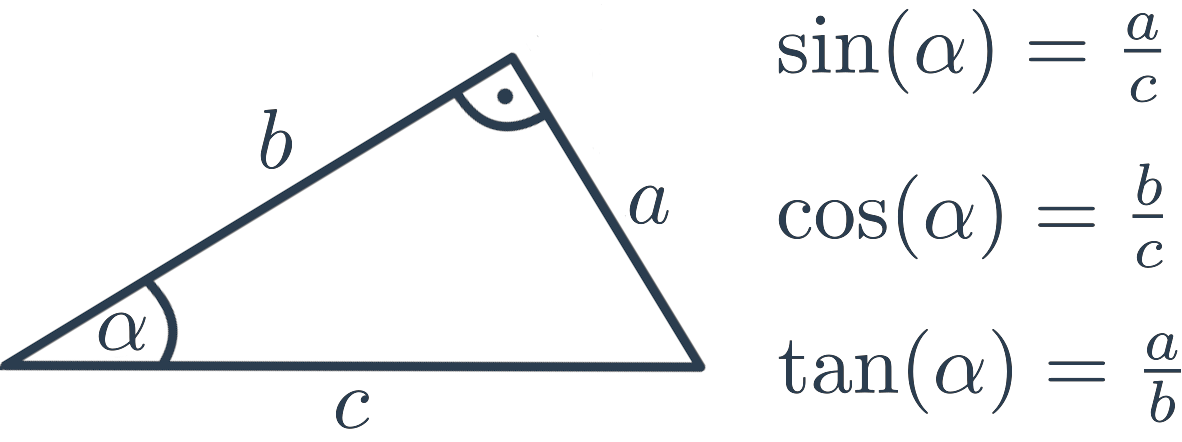Goniometrické funkce a pravoúhlý trojúhelník

Goniometrické funkce můžeme v pravoúhlém trojúhelníku vyjádřit následovně:
- Sinus (\sin) úhlu \alpha je poměr délky odvěsny protilehlé úhlu \alpha a délky přepony.
- Kosinus (\cos) úhlu \alpha je poměr délky odvěsny přilehlé úhlu \alpha a délky přepony.
- Tangens (\tan) úhlu \alpha je poměr délky odvěsny protilehlé úhlu \alpha a délky odvěsny přilehlé úhlu \alpha.
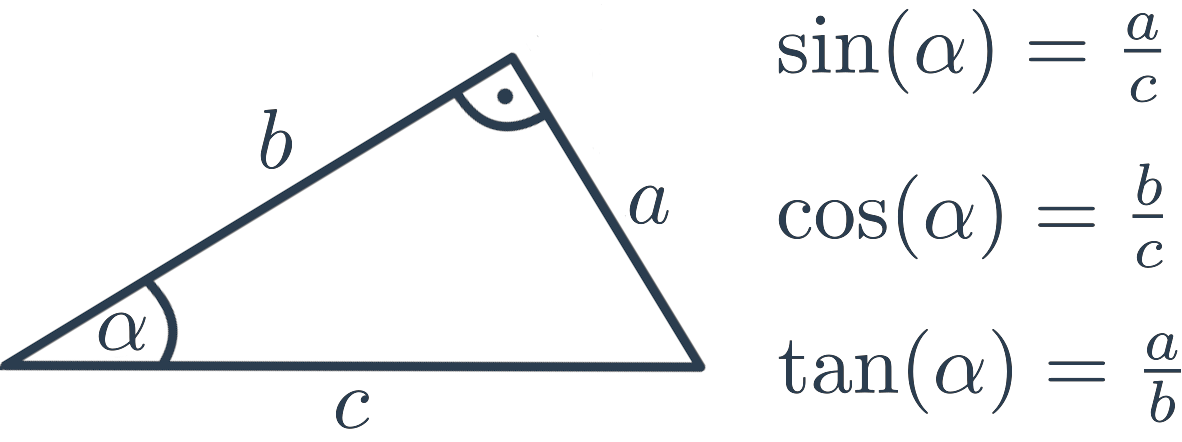
Pokud si pamatujeme význačné hodnoty goniometrických funkcí (jako např. \sin 30^{\circ}=\frac{1}{2}), nebo aspoň máme k dispozici kalkulačku nebo matematické tabulky, znamená pro nás znát hodnotu \sin, \cos nebo \tan některého úhlu v pravoúhlém trojúhelníku totéž jako znát velikost samotného úhlu.
Příklad: známe strany pravoúhlého trojúhelníku, dopočítáme úhly
Pravoúhlý trojúhelník ABC má délky stran a=24, b=10, c=26. Jaké jsou velikosti jeho vnitřních úhlů?
- Pokud je trojúhelník pravoúhlý, je velikost úhlu \gamma naproti nejdelší straně c rovna 90^{\circ}.
- Víme, že \sin \alpha je podíl protilehlé strany a přepony, tedy \sin \alpha=\frac{a}{c}.
- Dosadíme známé velikosti stran: \sin \alpha = \frac{24}{26}\doteq 0{,}923
- Příslušná velikost úhlu je: \alpha \doteq 67^{\circ}
- Z \alpha+\beta+\gamma=180^{\circ} dopočítáme, že \beta je zhruba 23^{\circ}.
Kontrola:
- Víme, že \cos \beta je podíl strany přilehlé k úhlu \beta a přepony, tedy \cos \beta = \frac{a}{c}.
- Dosadíme známé velikosti stran: \cos \beta = \frac{24}{26}\doteq 0{,}923
- Příslušná velikost úhlu je: \beta \doteq 23^{\circ}
Příklad: známe úhel, dopočítáme délku strany pomocí \sin
Mějme pravoúhlý trojúhelník ABC s pravým úhlem u vrcholu C, ve kterém platí \sin \alpha = \frac{1}{2} a délka přepony je c=10. Jaká je délka strany a?
- Víme, že hodnotu \sin \alpha spočítáme jako podíl délky strany protilehlé k úhlu \alpha a délky přepony, tedy \sin \alpha = \frac{a}{c}.
- Dosadíme do této rovnosti za \sin \alpha a za c.
- \frac{1}{2} = \frac{a}{10} \Rightarrow a=5
- Délka strany a je 5.
Příklad: známe úhel, dopočítáme délku strany pomocí \cos
Mějme pravoúhlý trojúhelník ABC s pravým úhlem u vrcholu C, ve kterém platí \cos \alpha = \frac{3}{5} a délka přepony je c=15. Jaká je délka strany a?
- Víme, že hodnotu \cos \alpha spočítáme jako podíl délky strany přilehlé k úhlu \alpha a délky přepony, tedy \cos \alpha = \frac{b}{c}.
- Dosadíme do této rovnosti za \cos \alpha a za c.
- \frac{3}{5} = \frac{b}{15} \Rightarrow b=9
- Délka strany b je 9. Chtěli jsme spočítat délku strany a, což zvládneme ze známých hodnot b,c jednoduše pomocí Pythagorovy věty.
- a^2 = c^2-b^2=255-81=144 \Rightarrow a=12
- Délka strany a je 12.
Příklad: známe úhel, dopočítáme délku strany pomocí \tan
Mějme pravoúhlý trojúhelník ABC s úhlem \alpha = 60^{\circ} a s délkou delší odvěsny 6. Jaká je délka druhé odvěsny?
- Víme, že v pravoúhlém trojúhelníku ABC jsou vnitřní úhly 60^{\circ}, 90^{\circ}, dopočítáme zbývající úhel.
- \beta=180^{\circ}-60^{\circ}-90^{\circ}=30^{\circ}
- Vidíme, že \beta \lt \alpha.
- Delší odvěsna bude v trojúhelníku proti většímu úhlu, takže máme a=6.
- \tan \alpha je podíl odvěsny protilehlé úhlu \alpha a odvěsny přilehlé, tedy \tan \alpha = \frac{a}{b}.
- Dosadíme za \tan \alpha hodnotu \tan 60^{\circ} = \sqrt{3} (zjistíme z tabulek nebo z kalkulačky), dosadíme také b=6.
- \sqrt{3} = \frac{6}{b} \Rightarrow b= \frac{6}{\sqrt{3}} = 2\sqrt{3}
- Délka kratší odvěsny je b=2\sqrt{3}.
Zavřít