Podobnost (střední) – online Přesouvání

QR kód

Stáhnout Na celou obrazovku

Kód / krátká adresa

Zkopírujte kliknutím. Zkopírováno!

FPO

umime.to/FPO

Podobnost

Dva geometrické útvary jsou si podobné, pokud oba mají stejný tvar (bez ohledu na velikost). Na následujícím obrázku mají podobné útvary stejnou barvu:

Přesněji řečeno, útvary jsou podobné, pokud jeden můžeme získat z druhého kombinací rovnoměrného zmenšení či zvětšení a následným posunutím, otočením nebo překlopením.

Podobnost zachovává velikost úhlů a poměr délek.

Poměr délek odpovídajících úseček v obou útvarech se nazývá koeficient podobnosti.

Příklad 1

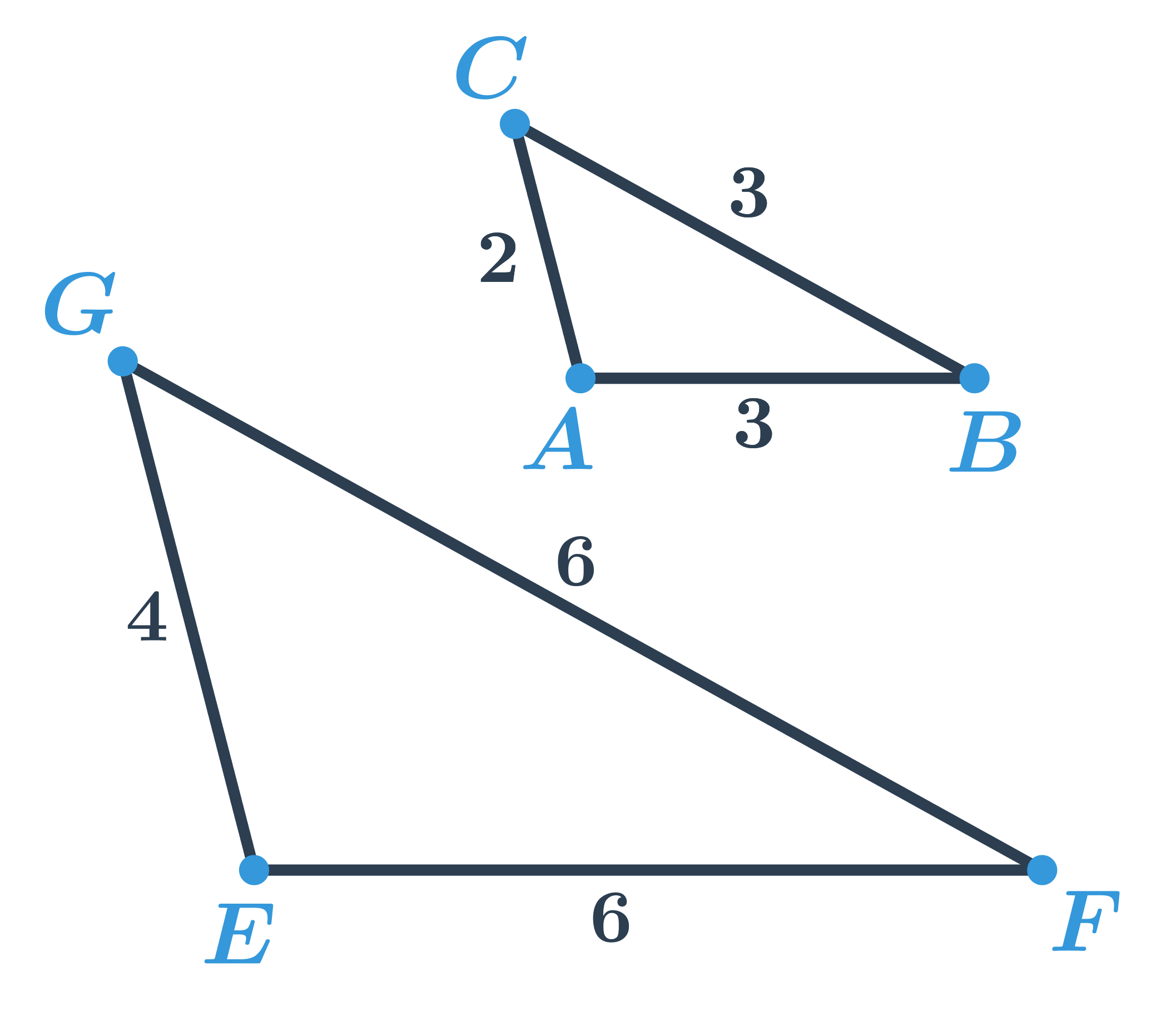
Trojúhelníky ABC a EFG jsou si podobné, protože poměr délek odpovídajících stran je stejný:

\frac{EF}{AB}=\frac{6}{3}=2
\frac{FG}{BC}=\frac{6}{3}=2
\frac{GE}{CA}=\frac{4}{2}=2

Zapisujeme \bigtriangleup EFG\sim \bigtriangleup ABC, koeficient podobnosti je 2.

Příklad 2

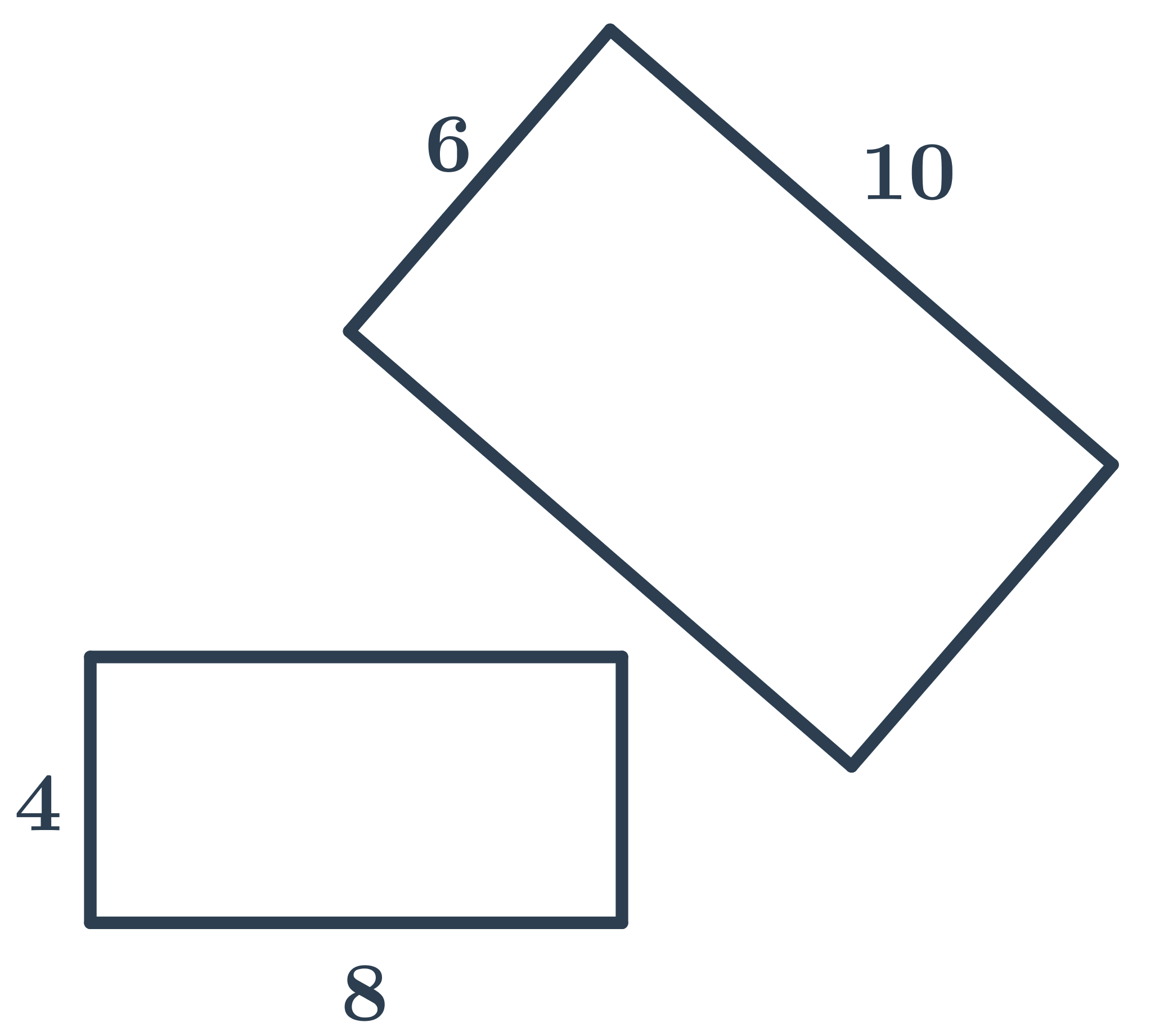
Obdélníky na obrázku nejsou podobné, protože poměr délek odpovídajících stran není stejný:

poměr delších stran je \frac{10}{8}=\frac{5}{4}
poměr kratších stran je \frac{6}{4}=\frac{3}{2}

Zavřít

Podobnost (střední)

VymažNevím VyhodnoťŘešeníDalší »

Vyřešeno:

QR kód

Kód / krátká adresa

umime.to/FPO

Podobnost

Děkujeme za vaši zprávu, byla úspěšně odeslána.

Napište nám

Nevíte si rady?

Čeho se zpráva týká?