Vlastnosti lineární lomené funkce

umime.to/G6G

Lineární lomená funkce f:y =\frac{ax+b}{cx+d} má definiční obor D(f)=\R - \{-\frac{d}{c}\}, což můžeme také zapsat jako sjednocení dvou intervalů: D(f)=(-\infty, -\frac{d}{c}) \cup (-\frac{d}{c}, \infty)

Pokud c\neq0 a bc-ad\neq0, pak pro lineární lomenou funkci platí:

je prostá
není periodická
nemá maximum ani minimum
není shora ani zdola omezená

Další vlastnosti závisí na hodnotách koeficientů a, b, c, d:

pro bc-ad \gt 0 je lineární lomená funkce klesající na intervalu (-\infty, -\frac{d}{c}) a také klesající na intervalu (-\frac{d}{c}, \infty)
pro bc-ad \lt 0 je lineární lomená funkce rostoucí na intervalu (-\infty, -\frac{d}{c}) a také je rostoucí na intervalu (-\frac{d}{c}, \infty)
pro a=0 a d=0 má lineární lomená funkce tvar: f:y =\frac{b}{cx} a je to lichá funkce (f(x) = - f(-x))

Příklad: vlastnosti funkce f:y =\frac{3x+1}{4x+2}

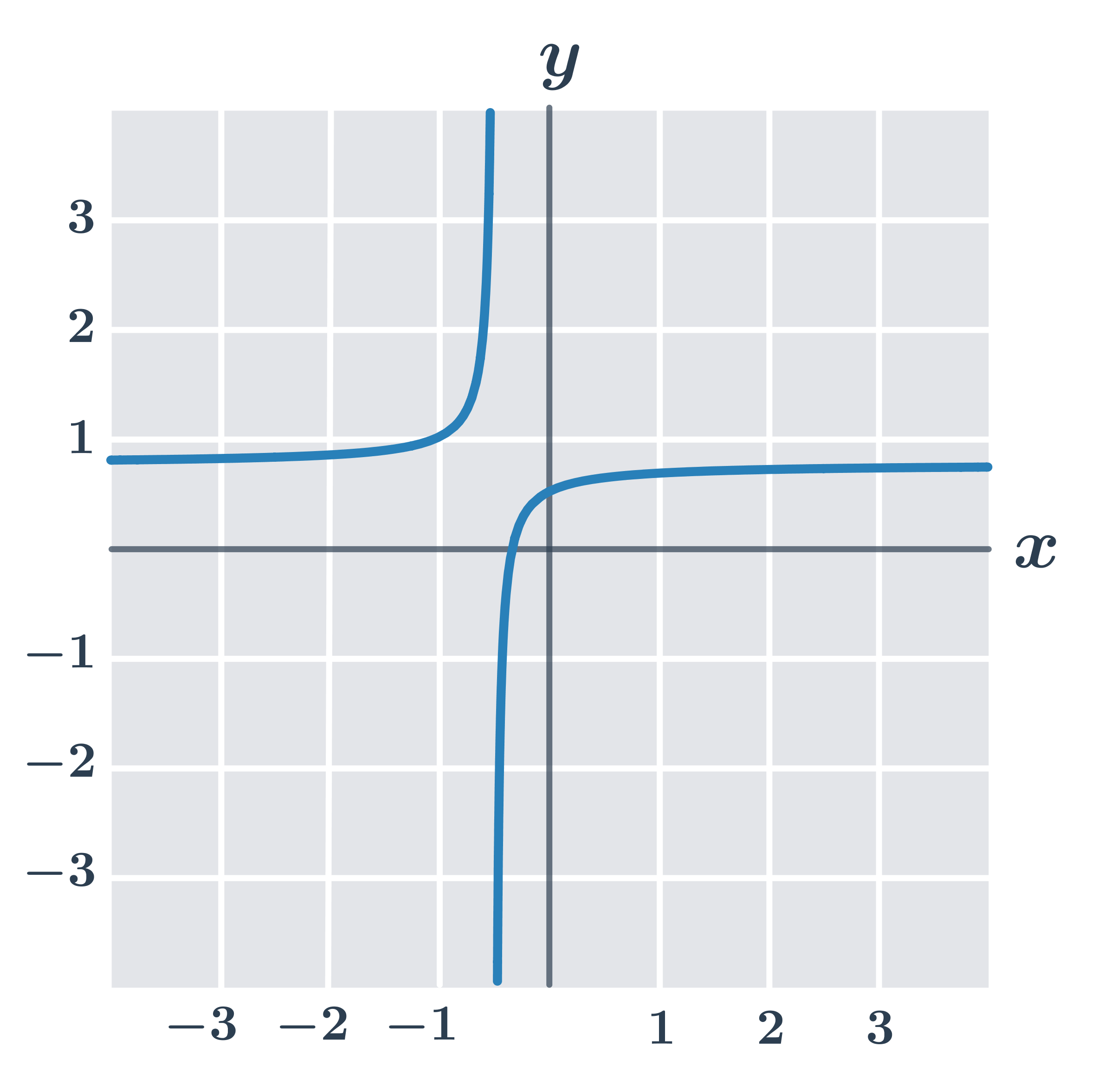
Definiční obor D(f)=\R - \{-\frac{1}{2}\}.
Funkce je prostá.
Funkce je rostoucí na intervalu (-\infty,-\frac{1}{2}) a také je rostoucí na intervalu (-\frac{1}{2},\infty) – snadno poznáme z grafu, ale zároveň můžeme ověřit splnění podmínky bc-ad \lt 0: pro danou funkci bc-ad=1\cdot4-3\cdot2=-2.

Příklad: vlastnosti funkce f:y =\frac{3}{2x}

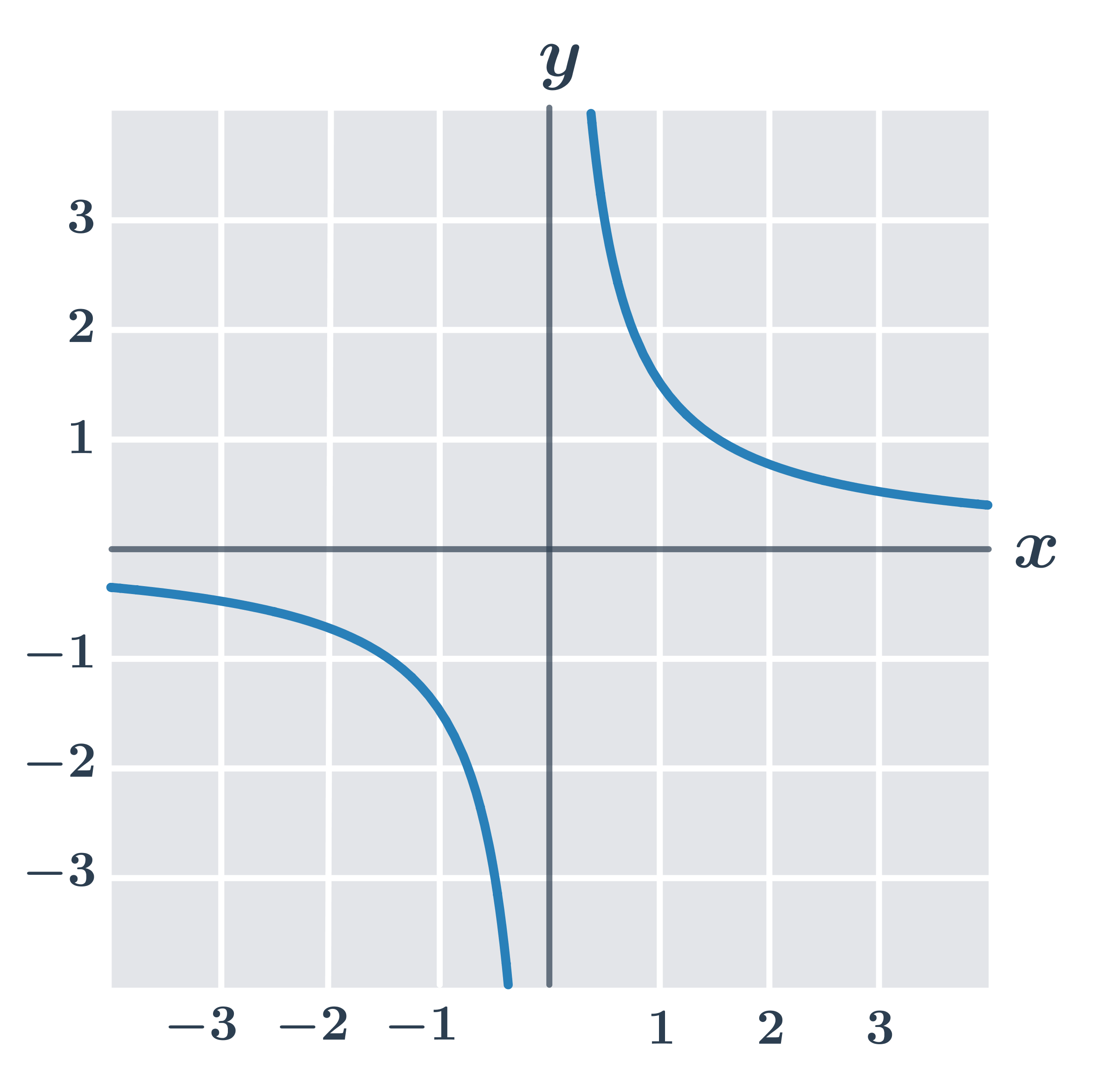
Definiční obor D(f)=\R - \{0\}.
Funkce je prostá.
Funkce je klesající na intervalu (-\infty,0) a také je klesající na intervalu (0,\infty).
Funkce je lichá – graf je souměrný podle počátku (pro lineární lomené funkce, kde a=0 a d=0).

Poznámka: omezenost lineární lomené funkce

Definiční obor lineární lomené funkce tvoří vždy dva intervaly.
Pokud si budeme všímat vlastností funkce jen na jednom z těchto intervalů, jedná se o funkci omezenou zdola nebo shora. Například funkce na obrázku f:y =\frac{2x+3}{x+1}:

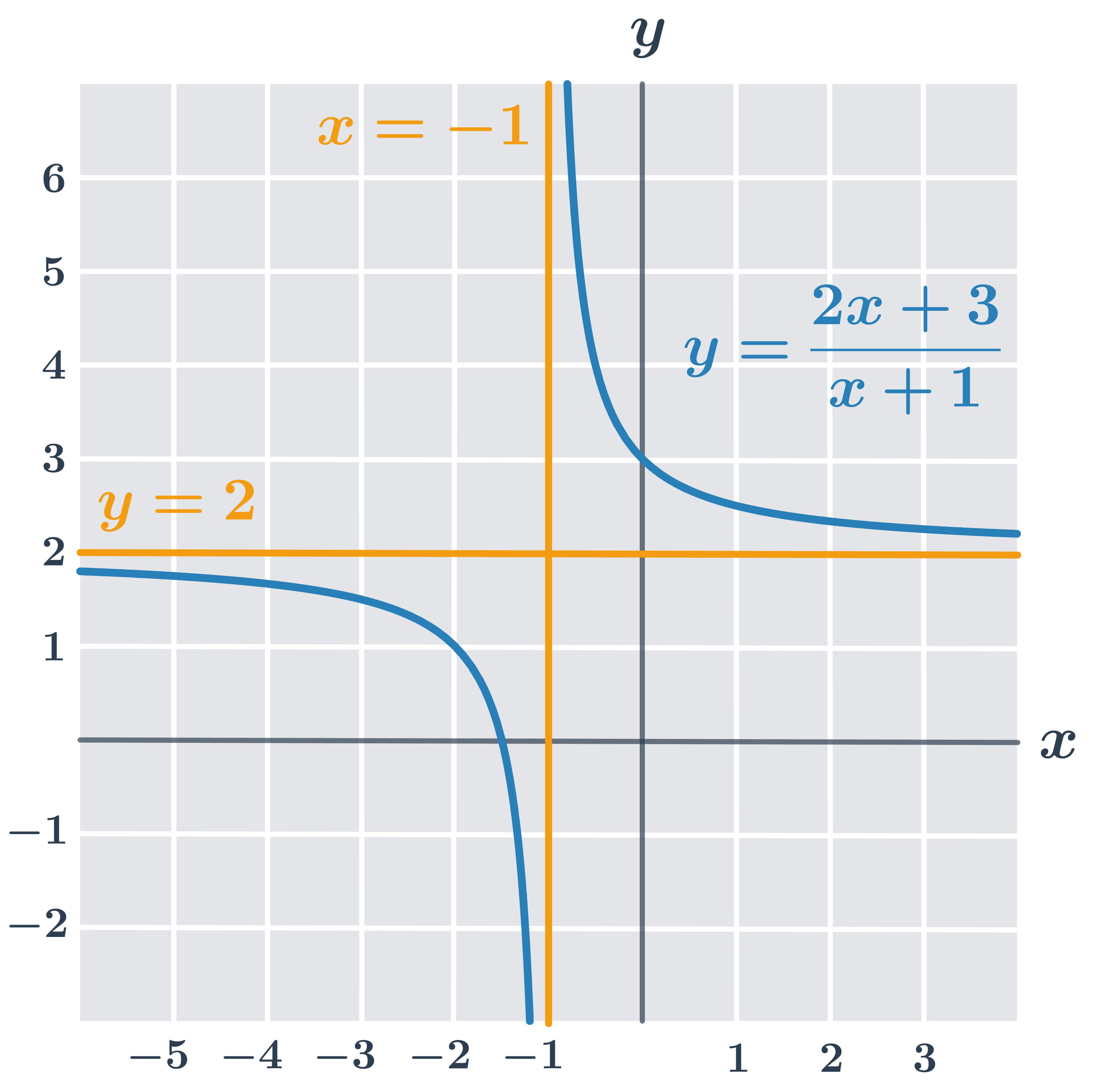
Definiční obor D(f)=\R - \{-1\}, tedy intervaly (-\infty;-1) a (-1;\infty).
Na intervalu (-\infty;-1) je funkce shora omezená a na intervalu (-1;\infty) zdola omezená.

Pro toto téma zatím není dostupné žádné procvičování.

Vlastnosti lineární lomené funkce

umime.to/G6G

Děkujeme za vaši zprávu, byla úspěšně odeslána.

Napište nám

Nevíte si rady?

Čeho se zpráva týká?