Výpis souhrnů
Popisná statistika
Podtémata
Průměr a medián
Průměr a medián vyjadřují „typickou“ hodnotu proměnných z určitého vzorku, jsou to míry centrální (střední) tendence.
Průměr je součet hodnot vydělený jejich počtem. Přesněji řečeno jde o aritmetický průměr (existují i jiné druhy průměrů, např. harmonický či geometrický).
Medián je prostřední hodnota ze seřazené posloupnosti hodnot. Je definován jako hodnota větší nebo rovna polovině hodnot v souboru a menší nebo rovna polovině hodnot v souboru.
Příklad: průměr a medián souboru 10, 3, 8, 4, 5
Uvažme soubor hodnot 10, 3, 8, 4, 5.
- Průměr je součet dělený počtem, tj. 30:5=6.
- Pro určení mediánu hodnoty nejdříve seřadíme: 3, 4, 5, 8, 10.
- Medián je prostřední hodnota, tedy 5.
Pokud má soubor sudý počet prvků, většinou se za medián označuje průměr dvou prostředních hodnot.
Příklad: medián souboru 10, 2, 9, 4, 14, 5
Uvažme soubor se sudým počtem hodnot 10, 2, 9, 4, 14, 5.
- Seřazená posloupnost je 2, 4, 5, 9, 10, 14.
- Hodnoty uprostřed posloupnosti jsou 5 a 9, medián je tedy 7.
Někdy máme soubor hodnot, které lze uspořádat podle velikosti, ale není možné vypočítat aritmetický průměr dvou hodnot.
Příklad: medián souboru S, M, XL, XXL
Uvažme soubor čtyř hodnot S, M, XL, XXL velikostí oblečení.
- Pro něj splňuje definici mediánu jakákoliv hodnota od M do XL, tedy M, L, i XL.
Kvantily a kvartily
Kvantily jsou charakteristiky polohy statistického znaku podobně jako např. aritmetický průměr a medián. Kvantily lze určit pro ordinální, intervalové a poměrové typy dat.
Soubor n hodnot uspořádáme podle velikosti: x_1 \le x_2 \le \ldots \le x_{n-1} \le x_n
Mějme číslo \theta mezi nulou a jedničkou. Kvantil Q_{\theta} je hodnota, která dělí uspořádanou posloupnost hodnot v souboru na dolní a horní část tak, že dolní část obsahuje alespoň \theta \cdot n hodnot a horní část alespoň (1-\theta)\cdot n hodnot.
x_1 \le \ldots \le x_c \le Q_{\theta} \le x_{c+1} \le \ldots \le x_n
- Je-li \theta \cdot n necelé číslo, a nejbližší větší celé číslo je k, volíme obvykle Q_{\theta}=x_k.
- Je-li \theta \cdot n=m celé číslo, volíme Q_{\theta} = \frac{x_{m}+x_{m+1}}{2} (pokud je možné tento aritmetický průměr spočítat – tedy pro intervalové a poměrové znaky).
Příklad: určení kvantilů Q_{0{,}1} a Q_{0{,}75} souboru 0,0,0,0,1,2,3,4
Vezmeme soubor osmi čísel 0,0,0,0,1,2,3,4.
- Kvantil Q_{0{,}1} určíme takto: 0{,}1 \cdot 8 = 0{,}8, nejbližší větší celé číslo je 1, takže Q_{0{,}1}=x_1=0.
- Kvantil Q_{0{,}75} určíme takto: 0{,}75 \cdot 8 = 6, takže Q_{0{,}75}=\frac{x_6+x_7}{2}=\frac{2+3}{2}=2{,}5.
Pro ordinální znaky nemusí být možné spočítat aritmetický průměr. Jako kvantil Q_{\theta} pak zvolíme některou hodnotu, která vhodně dělí uspořádanou posloupnost hodnot souboru.
Příklad: určení kvantilu Q_{0{,}8} souboru S, S, M, L, XXL
Spočítejme kvantil Q_{0{,}8} pro hodnoty S, S, M, L, XXL znaku „velikost oblečení“.
- 5 \cdot 0{,}8=4, takže Q_{0{,}8} je jakákoliv hodnota mezi x_4 a x_5, tedy L,XL, nebo XXL.
p% kvantil Q_{\frac{p}{100}} se nazývá p. percentil.
Některé významné kvantily:
| kvantil | název | |
|---|---|---|
| Q_{0{,}5} | medián | |
| Q_{0{,}25} | dolní kvartil | |
| Q_{0{,}75} | horní kvartil | |
| Q_{0{,}01},Q_{0{,}02},\ldots, Q_{0{,}99} | 1. percentil, 2. percentil, … , 99.percentil |
Mezikvartilové rozpětí je rozdíl horního a dolního kvartilu: Q_{0{,}75}-Q_{0{,}25} Mezikvartilové rozpětí (někdy označované jako IQR) lze spočítat pro intervalové a poměrové znaky.
Příklad: mezikvartilové rozpětí pro soubor 0,0,0,0,1,2,3,4
Určeme mezikvartilové rozpětí pro soubor osmi hodnot 0,0,0,0,1,2,3,4.
- Horní kvartil Q_{0{,}75} jsme už v předchozích příkladech spočítali, je to 2{,}5.
- Dolní kvartil Q_{0{,}25} je \frac{x_2+x_3}{2}=\frac{0+0}{2}=0.
- Mezikvartilové rozpětí je 2{,}5-0=2{,}5.
Absolutní a relativní četnost
Statistický soubor má rozsah n, pokud obsahuje právě n jednotek. Například statistickým souborem s rozsahem 10 může být skupinka 10 dětí ze třetí třídy. Jednotliví žáci a žákyně jsou pak jednotky statistického souboru.
Příklady statistických znaků, které nás mohou zajímat: jméno, výška, známka z prvouky. Předpokládejme, že jména dětí z naší skupinky deseti žáků a žákyň jsou: Anna, Eva, Jan, Jan, Jan, Vanesa, Vanesa, Mirka, Tobiáš, Tomáš.
Znak jméno tedy v našem statistickém souboru nabývá sedmi různých hodnot – Anna, Eva, Jan, Vanesa, Mirka, Tobiáš, Tomáš. Některé děti se mohou jmenovat stejně.
Absolutní četnost hodnoty znaku v daném statistickém souboru je počet jednotek ze statistického souboru, které mají danou hodnotu znaku.
Například absolutní četnost hodnoty „Jan“ znaku jméno je 3, protože ve skupince jsou tři žáci jménem Jan. Absolutní četnost hodnoty „Eva“ znaku jméno je 1.
Relativní četnost hodnoty znaku v daném statistickém souboru vypočítáme jako podíl počtu jednotek s danou hodnotou znaku počtem všech jednotek statistického souboru. Také se dá říci, že relativní četnost hodnoty znaku je podíl absolutní četnosti této hodnoty znaku a rozsahu n statistického souboru. Relativní četnost se zadává jako číslo v intervalu [0,1] nebo v procentech.
Například relativní četnost hodnoty „Vanesa“ znaku jméno je \frac{2}{10}=0{,}2, protože ve skupince celkem deseti dětí jsou dvě žákyně jménem Vanesa. Relativní četnost hodnoty „Vanesa“ znaku jméno můžeme zapsat také jako 20\ \%.
Součet absolutních četností všech hodnot jednoho znaku je roven rozsahu n daného statistického souboru.
Součet relativních četností všech hodnot jednoho znaku je 1 neboli 100\ \%.
NahoruKorelační koeficient
Korelace je vztah mezi dvěma veličinami. Korelační koeficient je číslo, které vyjadřuje sílu tohoto vztahu.
Existuje více způsobů, jak korelaci měřit. Nejčastěji používaný je Pearsonův korelační koeficient. Ten se značí r a má následující vlastnosti:
- Nabývá hodnot z intervalu [-1, 1].
- Měří pouze lineární závislost mezi veličinami.
- Pokud je hodnota kladná, odpovídá zvětšení jedné veličiny zvětšení druhé.
- Pokud je hodnota záporná, odpovídá zvětšení jedné veličiny zmenšení druhé.
- Pokud je hodnota nulová, není mezi veličinami lineární závislost.
- Pokud je hodnota přesně 1 nebo -1, je mezi veličinami přesná lineární závislost.
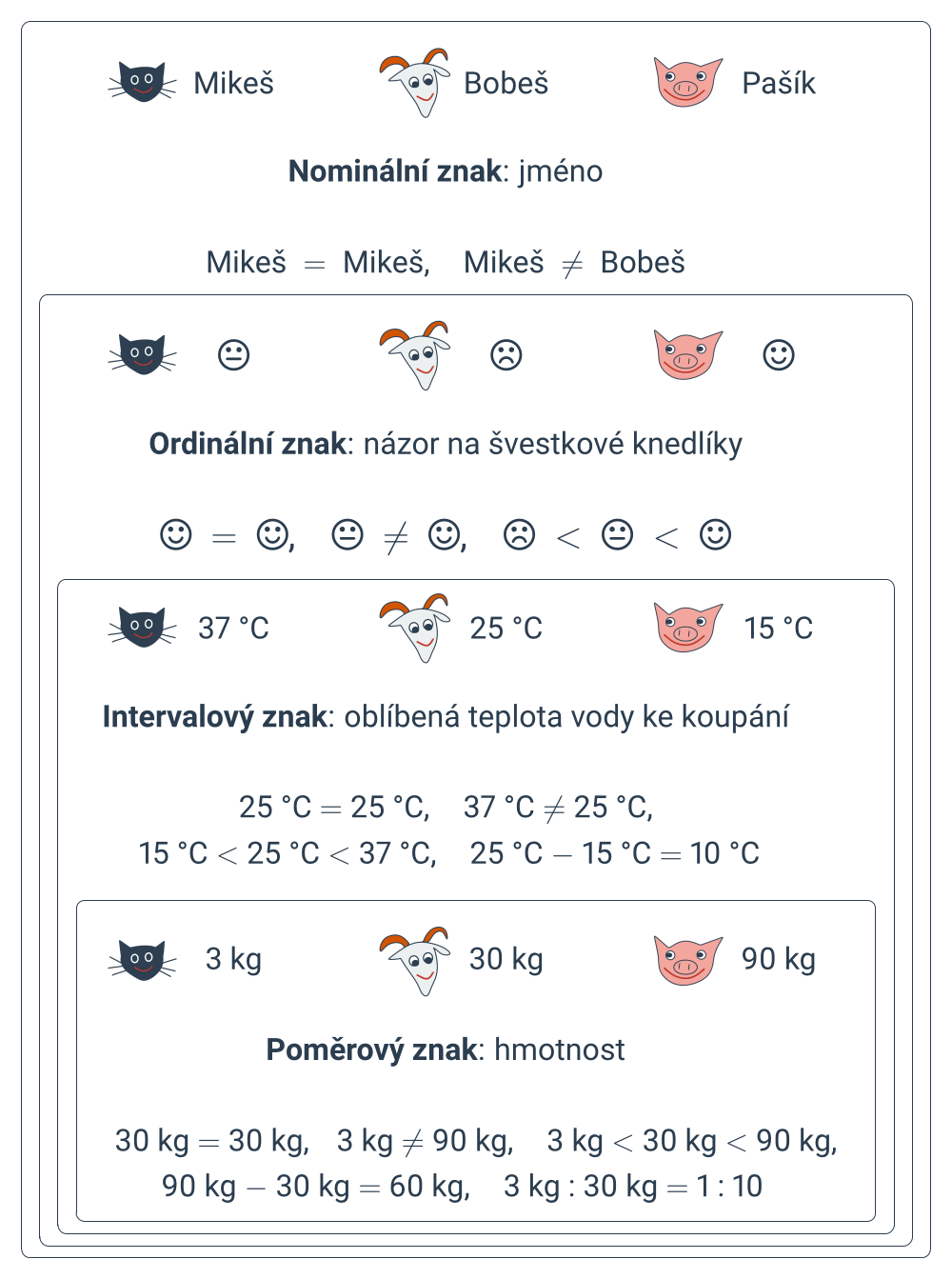
Typy statistických dat
Uvažujme statistický soubor zvířátek z Hrusic. Vezměme z něj tři jednotky na ukázku: kocourka Mikeše, kozla Bobeše a prasátko Pašíka. Budeme si u nich všímat různých typů znaků.
Nominální znak nabývá hodnot, u kterých můžeme testovat rovnost, tj. určit, jestli jsou stejné nebo různé. Například jméno, barva.
Ordinální znak nabývá hodnot, u kterých můžeme testovat rovnost a které navíc umíme porovnávat, tj. určit, která ze dvou různých hodnot je menší a která větší. Například známka z počtů, velikost oblečení (XS, S, M, L, XL), obliba brokolicové polívky („fuj“,„nic moc“,„mňam“).
Intervalový znak nabývá hodnot, u kterých můžeme testovat rovnost, porovnávat je a určit rozdíl dvou hodnot, tj. stejný interval mezi jednou a druhou dvojicí hodnot vyjadřuje i stejný rozdíl v intenzitě zkoumané vlastnosti. Například teplota ve stupních Celsia, rok narození.
Poměrový znak nabývá hodnot, u kterých můžeme testovat rovnost, porovnávat je, určit rozdíl dvou hodnot a určit poměr dvou hodnot, tj. spočítat jejich podíl, který smysluplně vyjadřuje kolikrát je jedna hodnota větší než druhá. Například teplota ve stupních Kelvina, hmotnost. Teplota ve stupních Celsia může jít i do záporných čísel a těleso o teplotě 10 °C nemá dvakrát větší kinetickou energii částic než těleso o teplotě 5 °C, takže teplota ve stupních Celsia není poměrový znak.
Alternativní znak je pojem mimo tuto hierarchii, znamená to, že znak nabývá pouze dvou hodnot. Například zdravý – nemocný, má boty – nemá boty.
Průměr, medián a modus (použití)
Aritmetický průměr, medián a modus jsou charakteristiky polohy znaku. Používáme je k popisu typické hodnoty znaku.
Aritmetický průměr pro daný soubor se počítá jako podíl součtu hodnot znaku a rozsahu souboru.
- Aritmetický průměr lze spočítat pro intervalové a poměrové znaky.
- Nejlépe se hodí k popisu typické hodnoty znaku, který nabývá v daném souboru podobných hodnot bez příliš odlišných extrémů, které by aritmetický průměr vychýlily mimo typické hodnoty.
Příklad použití aritmetického průměru – soubor hodnot 122, 116, 120, 118 znaku „výška dítěte v cm“ má aritmetický průměr 119.
Medián dělí řadu vzestupně seřazených hodnot na dvě stejně početné poloviny.
- Pro lichý počet hodnot je medián prostřední prvek.
- Pro sudý počet hodnot může definici mediánu odpovídat více hodnot, někdy se v takovém případě bere jako medián aritmetický průměr dvou prostředních hodnot (samozřejmě jen pokud lze pro daný znak aritmetický průměr spočítat).
- Medián lze určit pro ordinální, intervalové a poměrové znaky.
- Na rozdíl od aritmetického průměru není ovlivněn extrémními hodnotami.
Příklad použití mediánu – soubor hodnot 1, 1000, 1002, 1003 znaku „hmotnost krokodýla v kg“ má medián 1001 (nebo jakékoli číslo od 1000 do 1002). Extrémní malá hodnota 1 způsobí, že aritmetický průměr je 751{,}5, což neodpovídá typické hodnotě „něco málo přes 1000 kg“.
Modus je hodnota znaku, která má v daném souboru největší relativní (i absolutní) četnost.
- Takových hodnot může být víc než jedna.
- Modus můžeme spočítat pro nominální, ordinální, intervalové a poměrové znaky.
Příklad použití – modus souboru hodnot 1, 1, 1, 1, 2, 2 znaku „počet hrbů velblouda“ je 1.
Nahoru
