Hranol

Hranol je prostorový geometrický útvar, který má dvě shodné podstavy umístěné v různých rovinách. Budeme se zabývat kolmými hranoly, ve kterých odpovídající strany podstavy jsou vždy spojené boční stěnou tvaru obdélníka nebo čtverce. (Pro kosé hranoly jsou boční stěny rovnoběžníky.) Podstavy hranolu mohou mít rozličné tvary, například mohou být trojúhelníkové, čtvercové, obdélníkové nebo i mnohoúhelníkové.

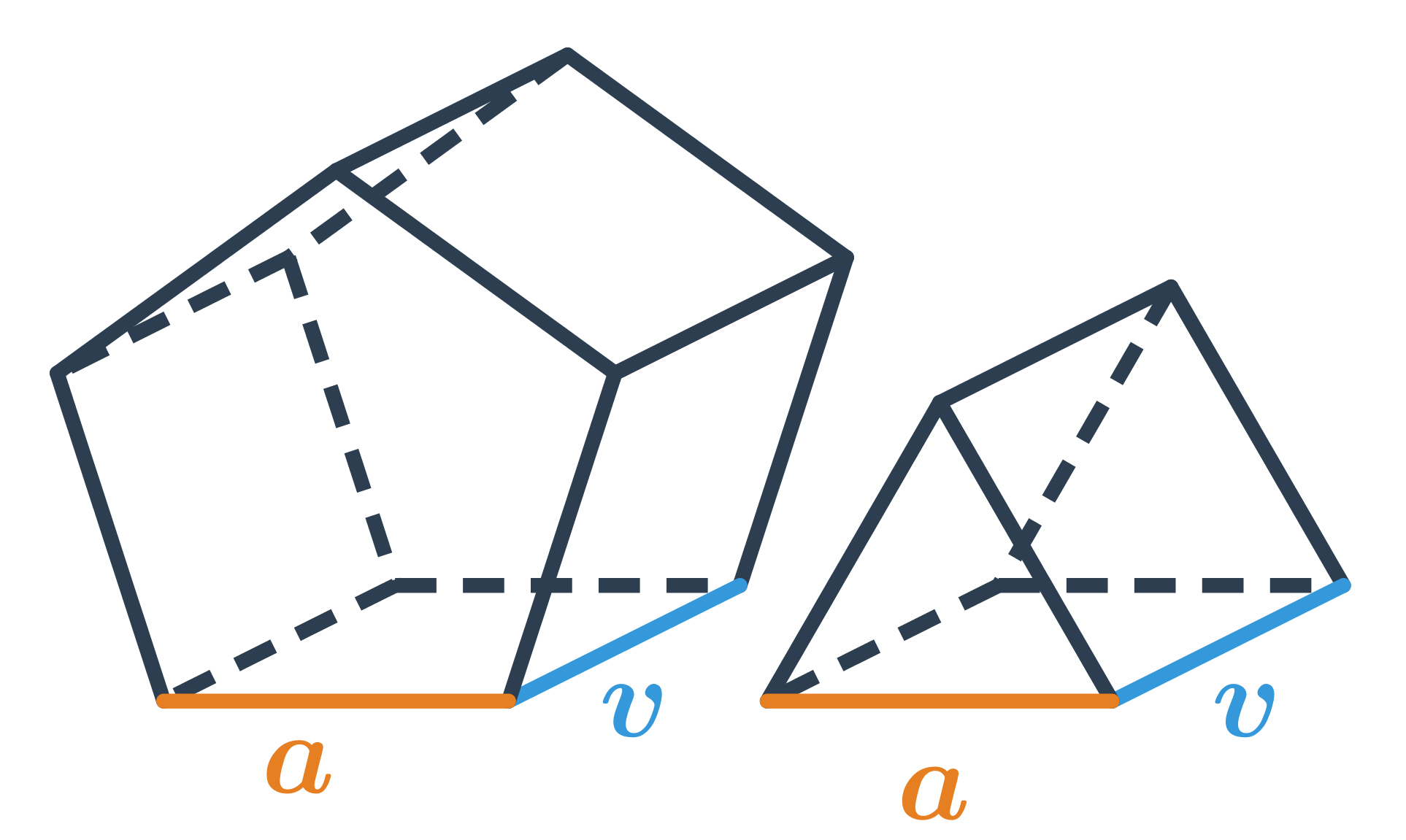
Vzorečky pro objem a povrch hranolu

Pro výpočet objemu hranolu používáme vzorec V = S_p \cdot v, kde S_p je obsah jedné podstavy a v je výška hranolu.

Síť hranolu se skládá ze dvou podstav a pláště, proto jeho povrch vypočítáme jako součet obsahů podstav a obsahu pláště: S = 2S_p + S_{pl}, kde S_{pl} je obsah pláště, což je součet obsahů všech obdélníkových nebo čtvercových stěn tvořících plášť.

Příklady hranolů

Pravidelný n-boký hranol má jako podstavy dva pravidelné n-úhelníky.

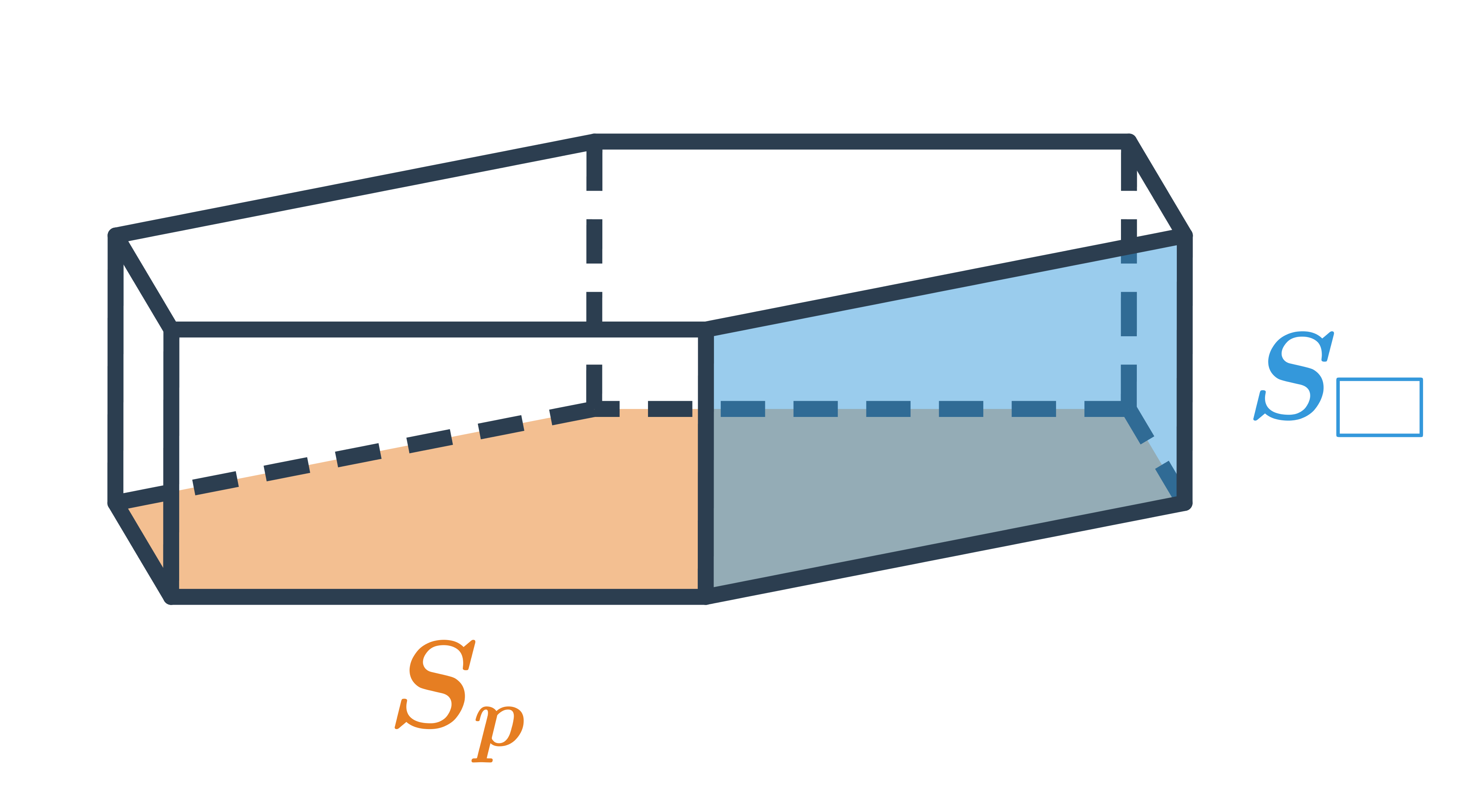
Speciální případy čtyřbokých hranolů jsou kvádr a krychle. Kvádr může a nemusí být pravidelný čtyřboký hranol. Krychle je pravidelný čtyřboký hranol, který navíc splňuje a=v.

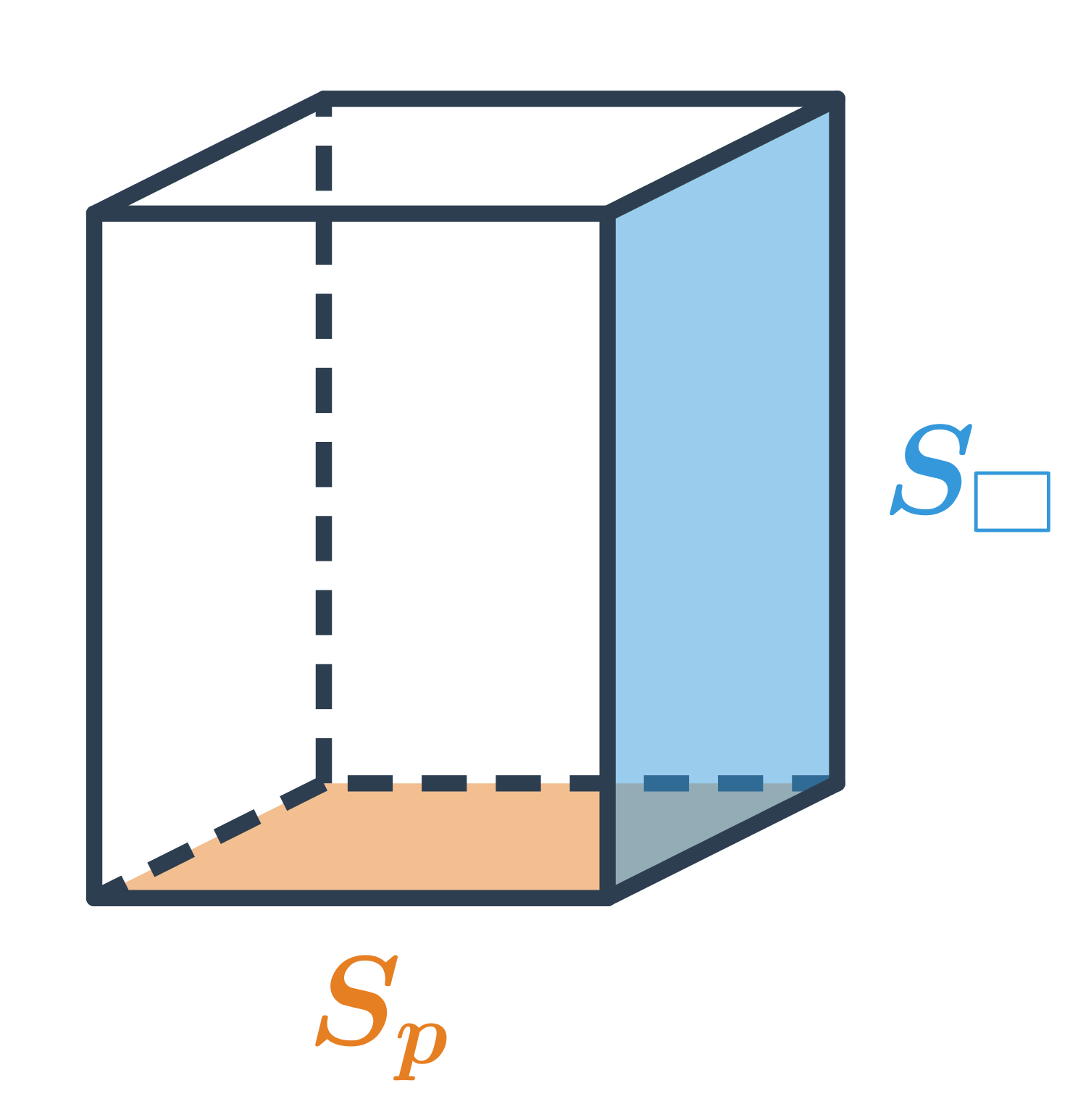
Objem hranolu, který má podstavu o obsahu S_p a výšku v, spočítáme jako V=S_p \cdot v.

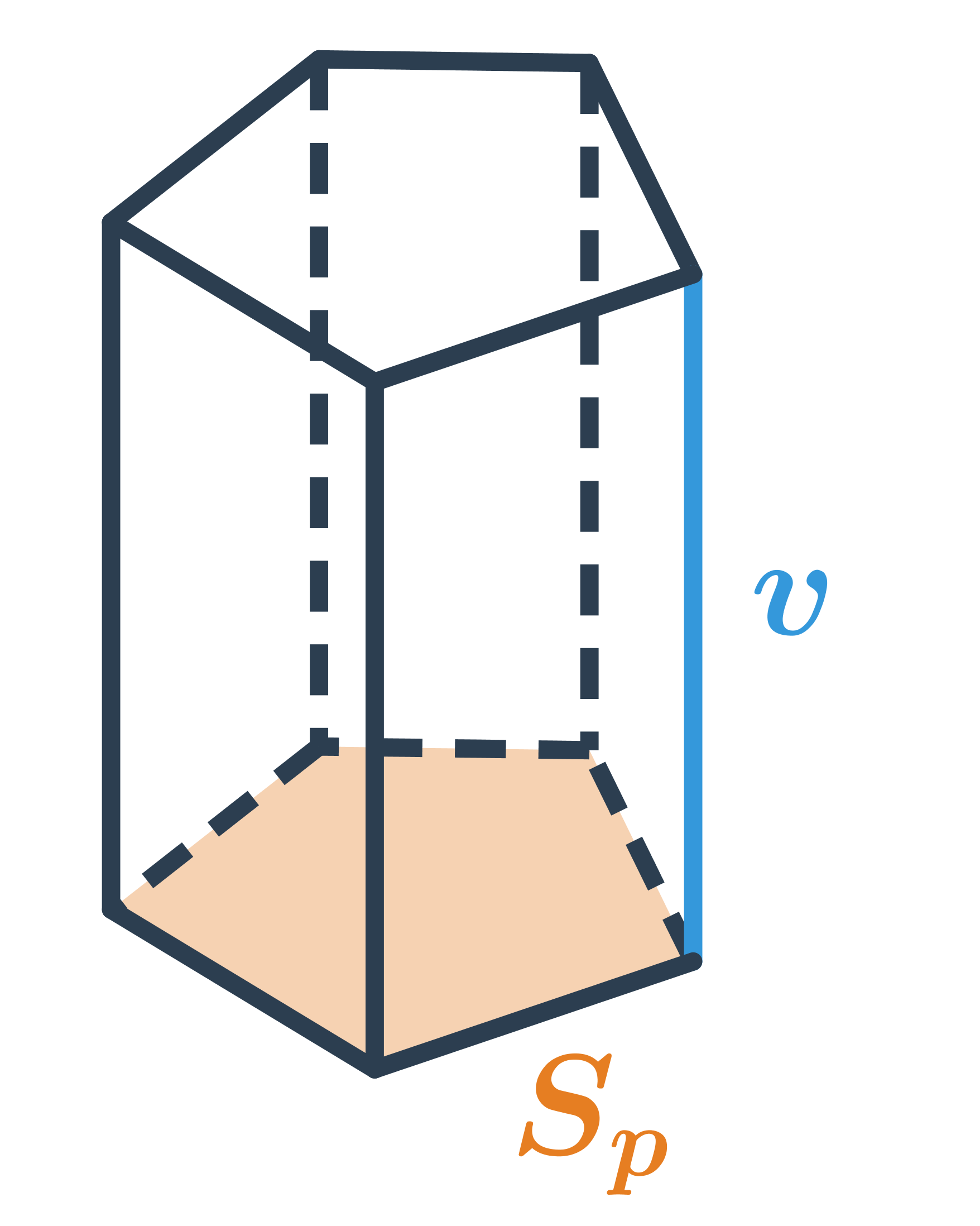
Povrch hranolu, který má podstavu o obsahu S_p plášť o obsahu S_{pl}, spočítáme jako S=2S_p + S_{pl}. Plášť hranolu je tvořen všemi jeho stěnami kromě dvou podstav.

Povrch pravidelného n‑bokého hranolu, který má dvě podstavy ve tvaru pravidelných n‑úhelníků a potom n stejných obdélníkových stěn (obsah jedné označme S_1), spočítáme takto: S=2S_p + n\cdot S_1