Výpis souhrnů
Exponenciální funkce
Podtémata
Exponenciální funkce
Funkce je exponenciální, pokud ji lze vyjádřit ve tvaru y= a^x, kde a je konstanta. Konstanta a se nazývá základ a může to být jakékoliv kladné reálné číslo kromě hodnoty 1, tedy a\in (0,1)\cup (1,\infty). Výraz x je exponent. Definičním oborem exponenciální funkce je množina všech reálných čísel, oborem hodnot je množina všech kladných reálných čísel. V běžné řeči používáme pojem exponenciální růst, pokud chceme říct, že něco velmi rychle roste, například počty nemocných při epidemii.
Příklad: exponenciální růst
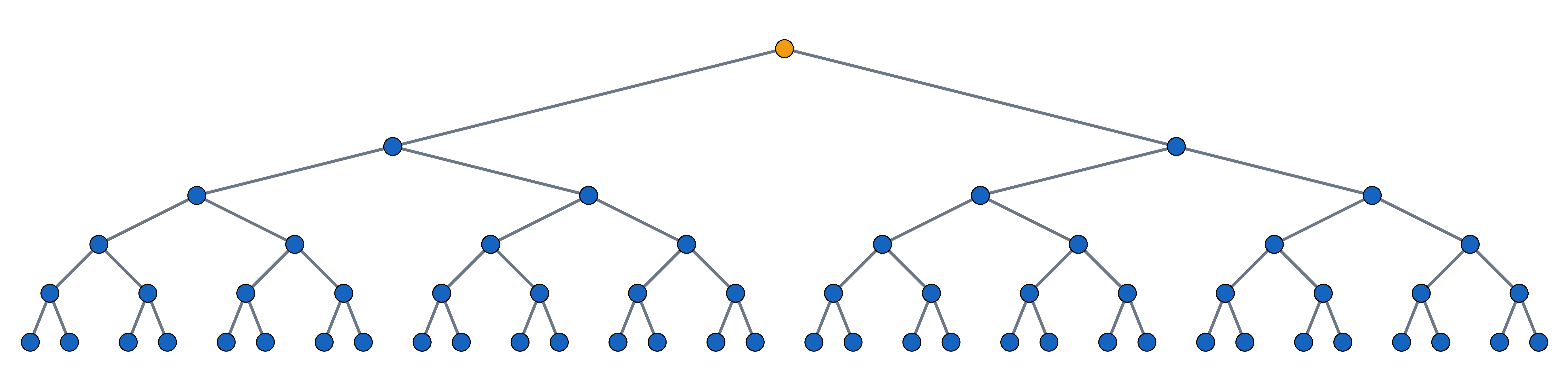
Nakažlivá nemoc se šíří exponenciálně. Budeme-li uvažovat exponenciální funkci se základem a=2, znamená to, že každý nemocný nakazí další dva lidi. Šíření nemoci se dá dobře znázornit obrázkem:
Vlastnosti exponenciálních funkcí
Pro exponenciální funkci f:y =a^x platí:
- definiční obor D(f)=\R
- obor hodnot H(f)=(0, \infty)
- je prostá
- není periodická
- není sudá ani lichá
- nemá maximum ani minimum
- je zdola omezená
Další vlastnosti závisí na hodnotě koeficientu a:
- pro a>1 je exponenciální funkce rostoucí
- pro a\in (0,1) je exponenciální funkce klesající
Příklad: vlastnosti funkce f\!: y =3^x
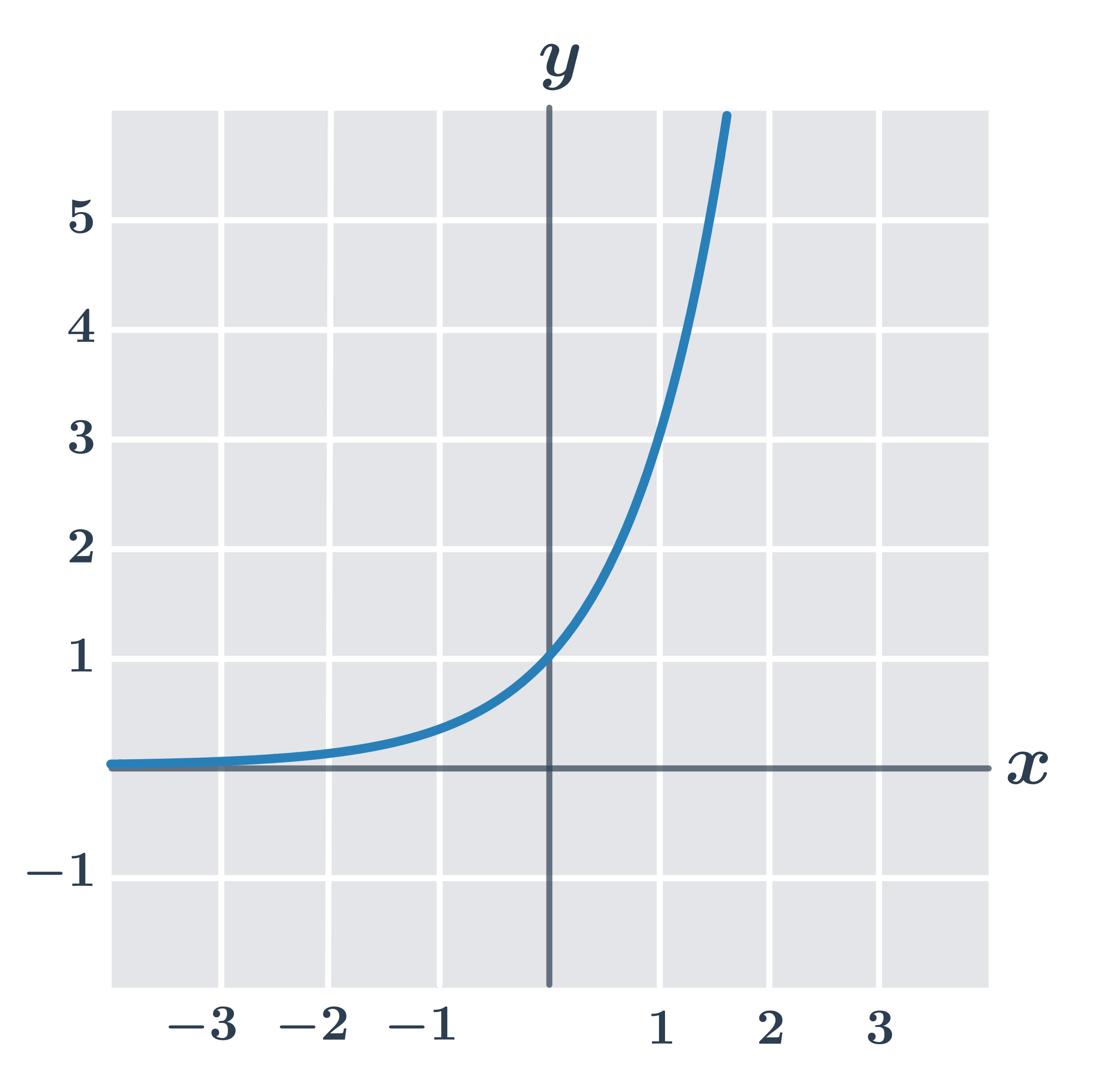
- definiční obor D(f)=\R
- obor hodnot H(f)=(0, \infty)
- je prostá
- je zdola omezená
- je rostoucí
Příklad: vlastnosti funkce f\!: y=\left (\frac{1}{2}\right)^x
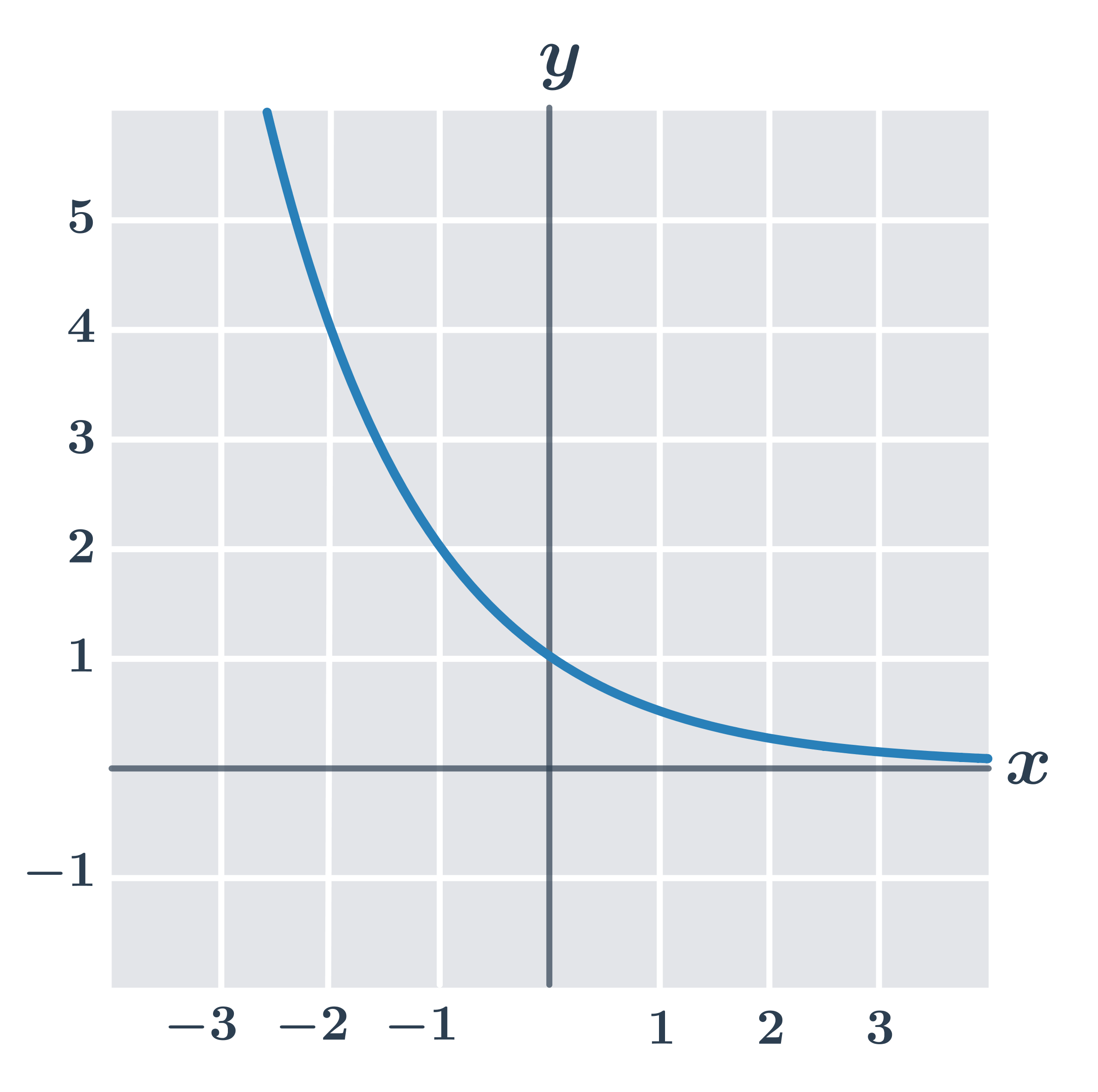
- definiční obor D(f)=\R
- obor hodnot H(f)=(0, \infty)
- je prostá
- je zdola omezená
- je klesající
Grafy exponenciálních funkcí
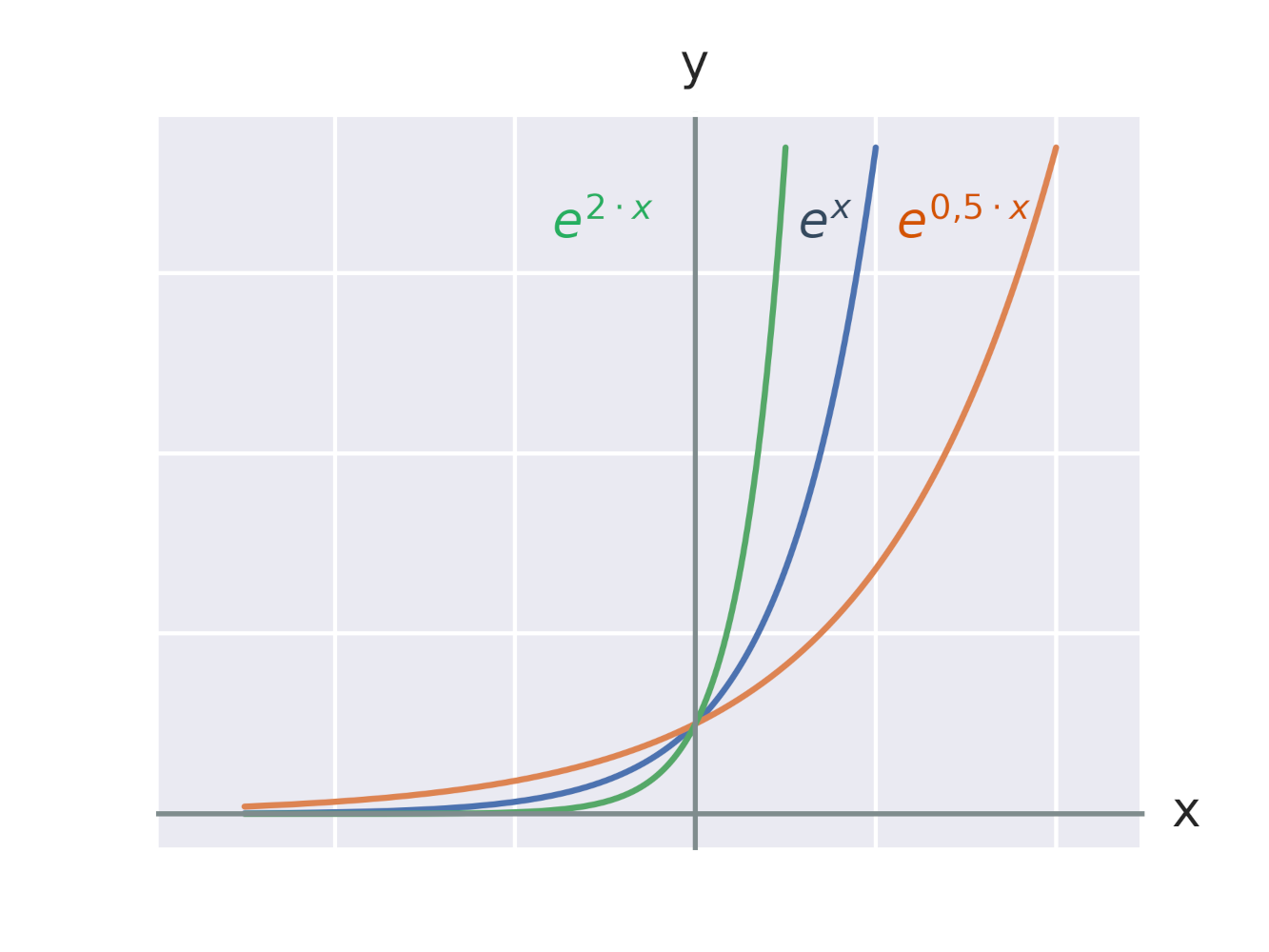
Grafem exponenciální funkce je křivka jménem exponenciála. Na obrázku jsou grafy exponenciálních funkcí se základy 2 a e = 2{,}7 182 818 284\ldots. Vidíme také, že grafy funkcí e^x a e^{-x} jsou spolu souměrné podle osy y.
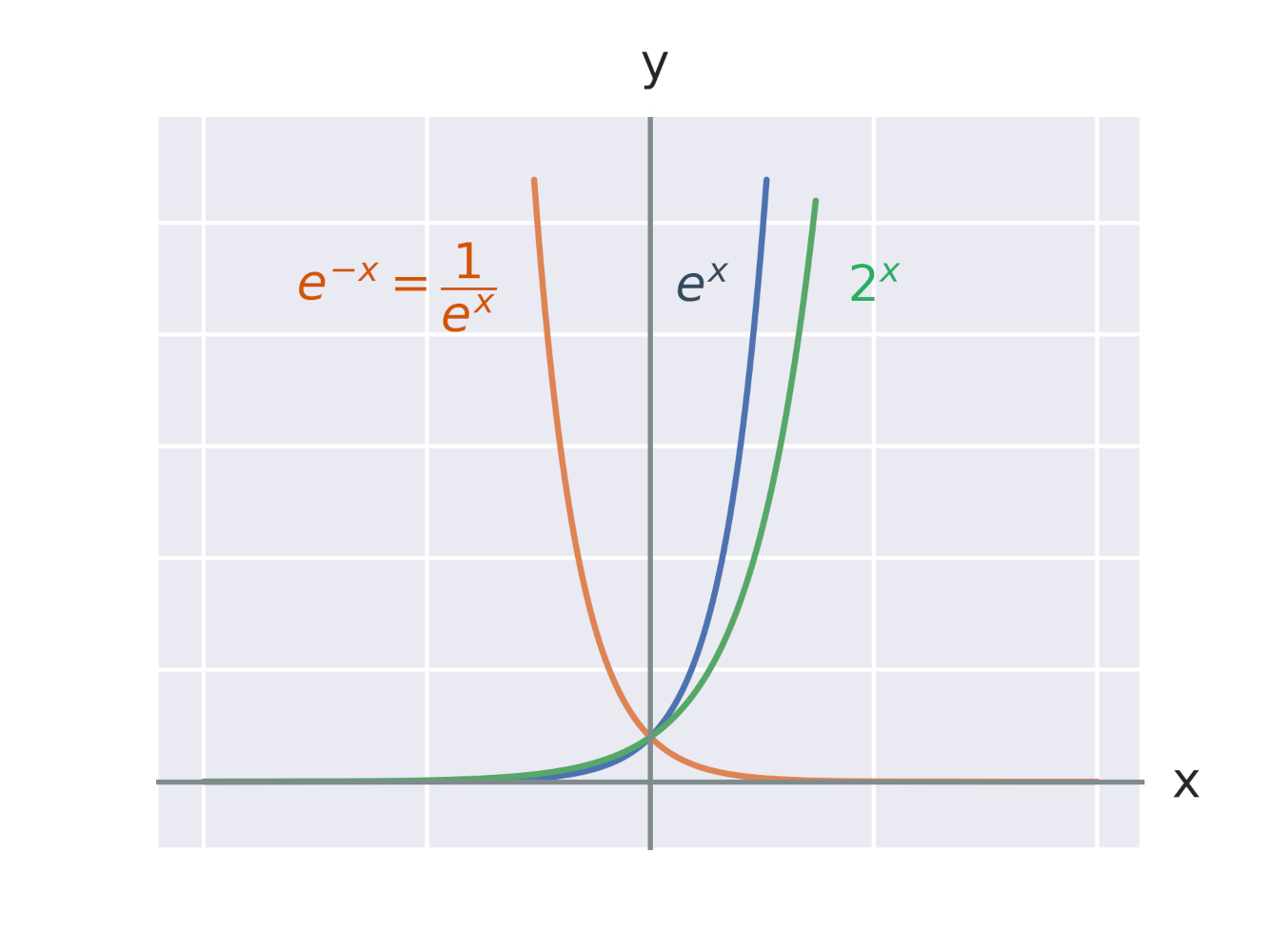
Graf každé exponenciální funkce tvaru f:y =a^x prochází bodem [0,1], protože pro libovolnou konstantu a platí: a^0=1.
Efekt přičtení konstanty k exponenciální funkci
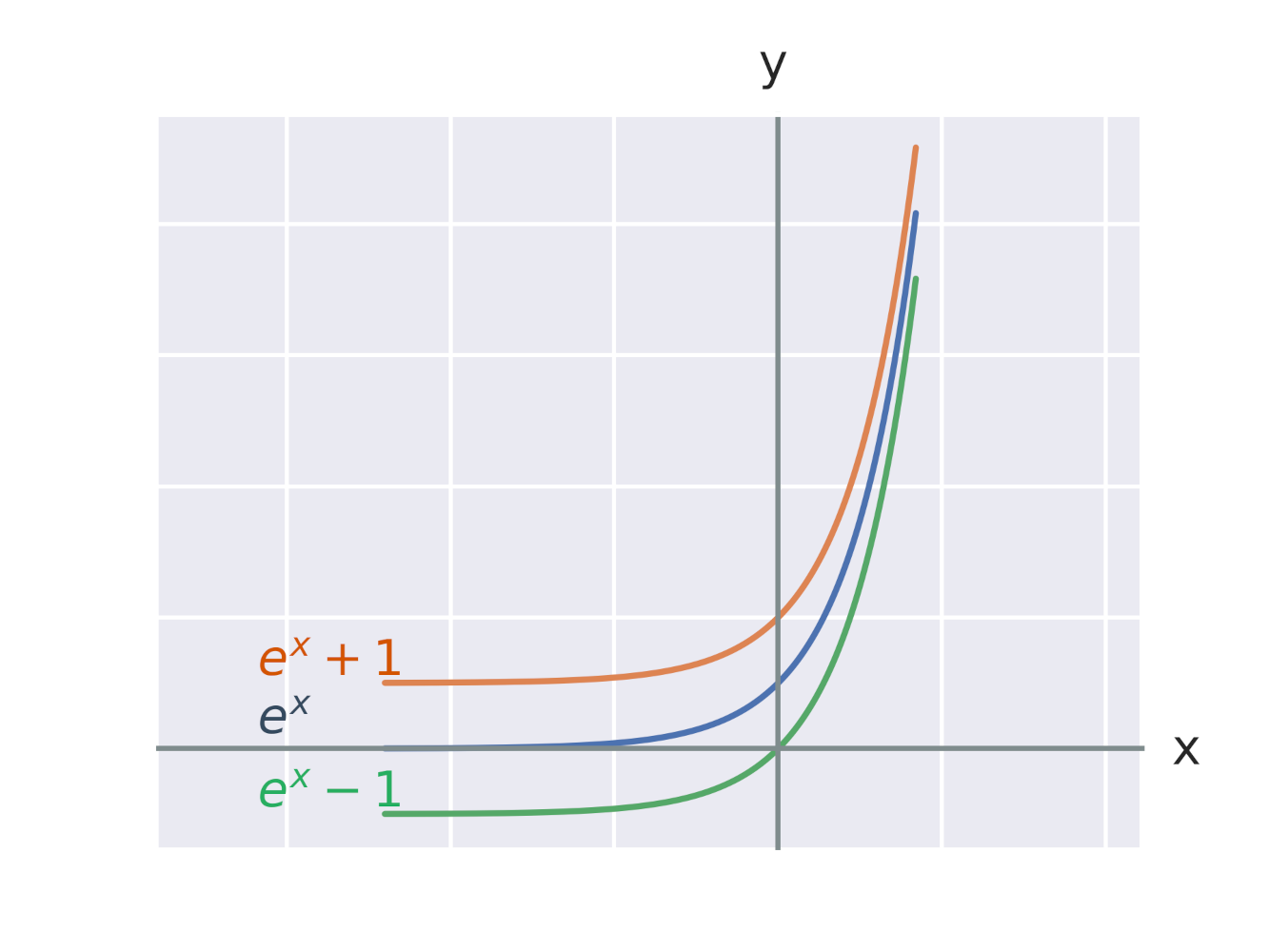
Efekt přičtení konstanty k exponentu
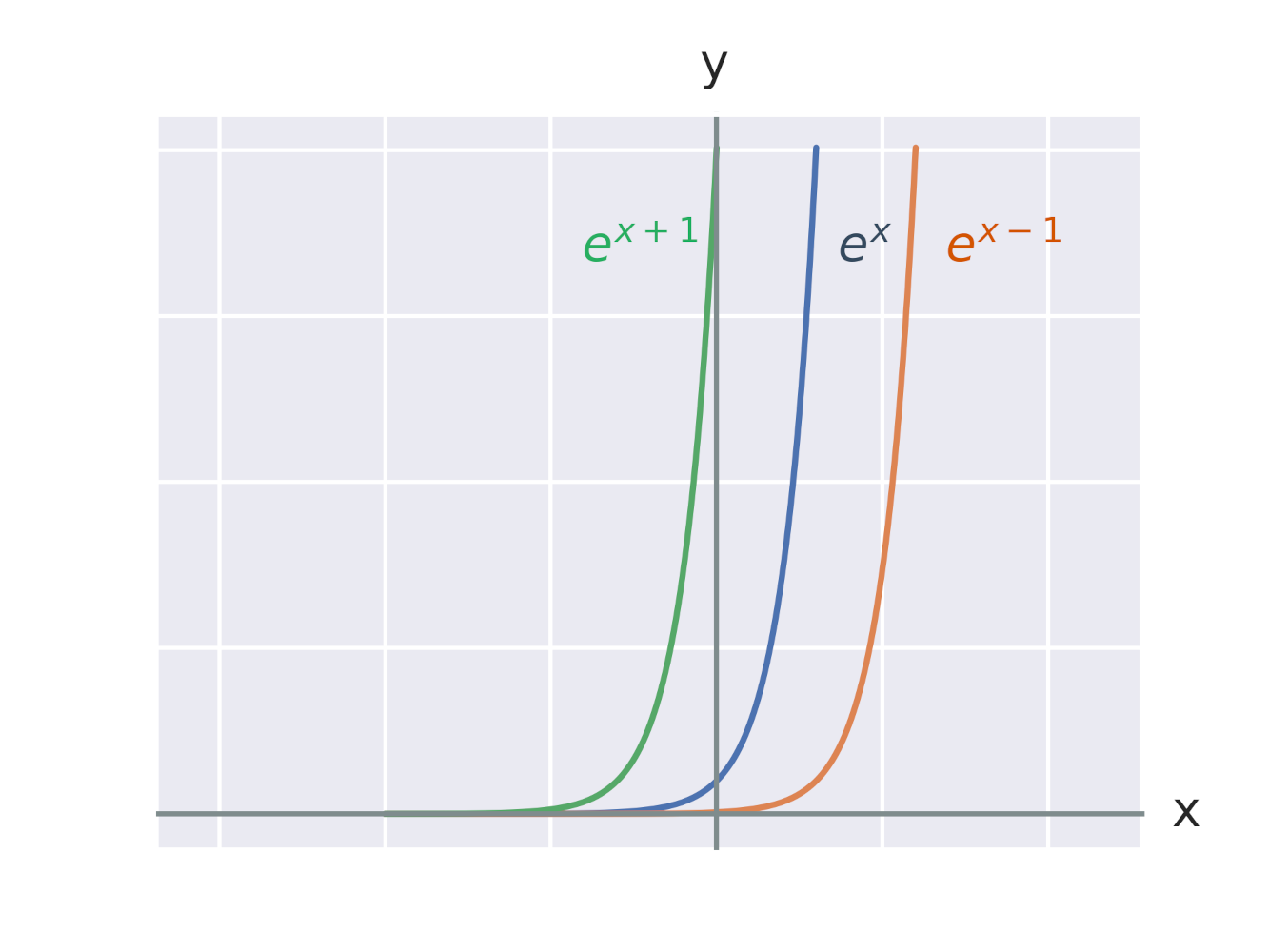
Efekt vynásobení exponenciální funkce konstantou
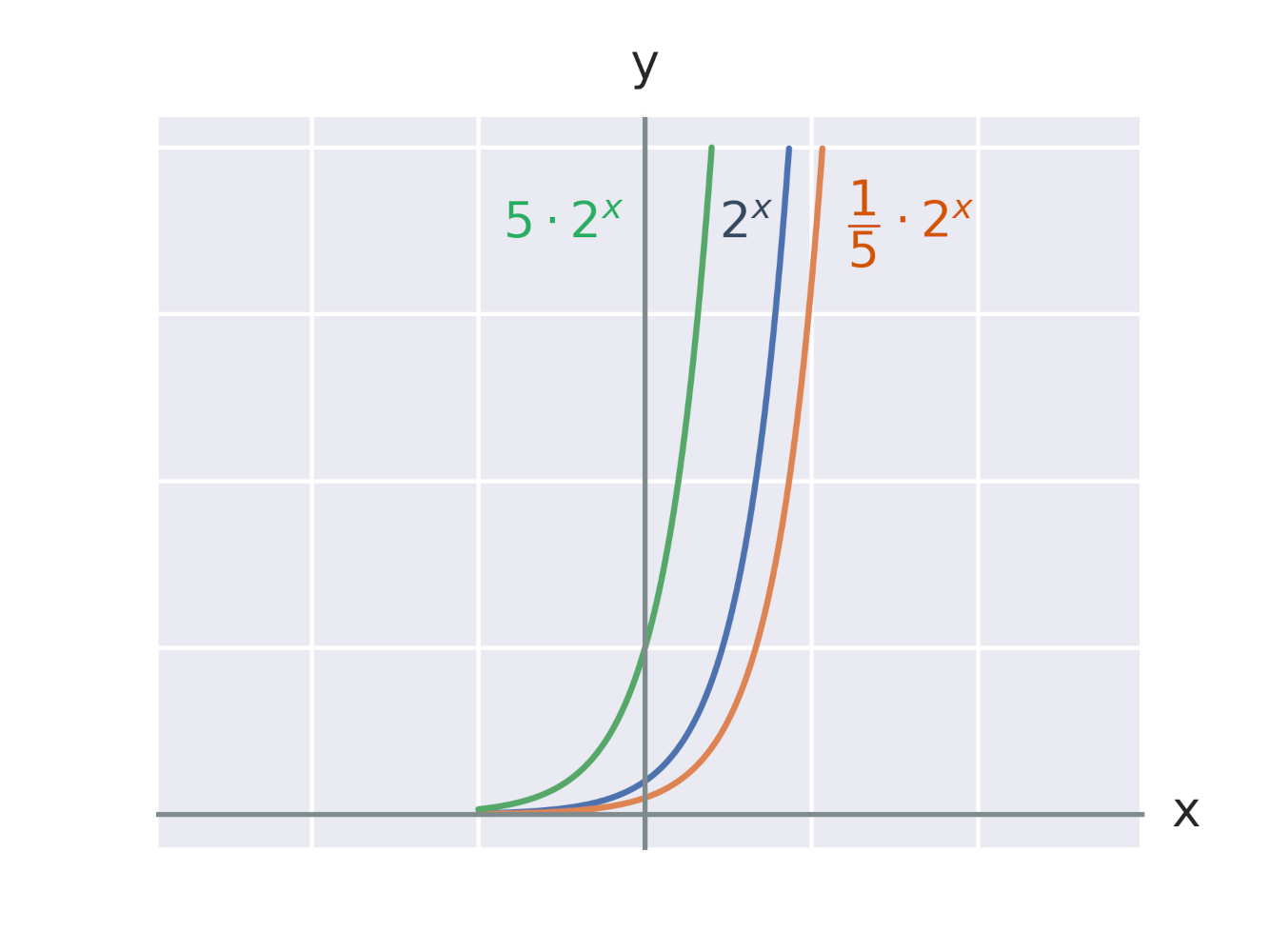
Efekt vynásobení exponentu konstantou