







Skvěle, štít %% dosažen
Geometrie » Rozhodovačka »
Geometrie
Rozhodovačka
QR kód
Kód / krátká adresa
Zkopírujte kliknutím. Zkopírováno!
Nastavení cvičení
Pozor, nastavení je platné pouze pro toto cvičení a předmět.
umime.to/GLT
Vzájemná poloha přímek v rovině
Vzájemnou polohu dvou přímek můžeme snadno určit, pokud známe souřadnice jejich směrových, případně normálových vektorů. Přímky rovnoběžné mají stejný směr, tedy jejich směrové vektory jsou kolineární. Normálové vektory dvou rovnoběžných přímek jsou také kolineární. Ve speciálním případě mohou být přímky totožné. Přímky různoběžné mají jeden společný bod, tento bod musí splňovat rovnice obou přímek. Jejich směrové vektory nejsou kolineární, normálové vektory také nejsou kolineární.
Rovnoběžky zadané parametrickými rovnicemi
Určete vzájemnou polohu dvou přímek p, q zadaných parametricky:
p: \begin{array}{rrl}x&=&-3+3t\\y&=&\hspace{0.25cm}2+t\\&&\hspace{0.25cm}t\in\mathbb{R}\end{array} \hspace{0.5cm}q: \begin{array}{rrl}x&=&1-3s\\y&=&2-s\\&&s\in\mathbb{R}\end{array}
- směrový vektor přímky p:\hspace{0.25cm}\vec{u}=(3;1)
- směrový vektor přímky q:\hspace{0.25cm}\vec{v}=(-3;-1)
- Přímky p a q jsou rovnoběžné, protože jejich směrové vektory jsou kolineární.
- Ověříme, že přímky nejsou totožné. Stačí určit, zda bod, který leží na jedné přímce neleží na přímce druhé.
- Na přímce p leží například bod A=[-3;2].
- Ověříme, že tento bod neleží na přímce q dosazením souřadnic bodu A do rovnic přímky q: \begin{array}{rrl}-3&=&1-3s \Rightarrow s=\frac{4}{3}\\2&=&2-\hspace{0.15cm}s\Rightarrow s=0\end{array}
- Vyšly různé hodnoty parametru s, takže bod A neleží na q \Rightarrow přímky nejsou totožné
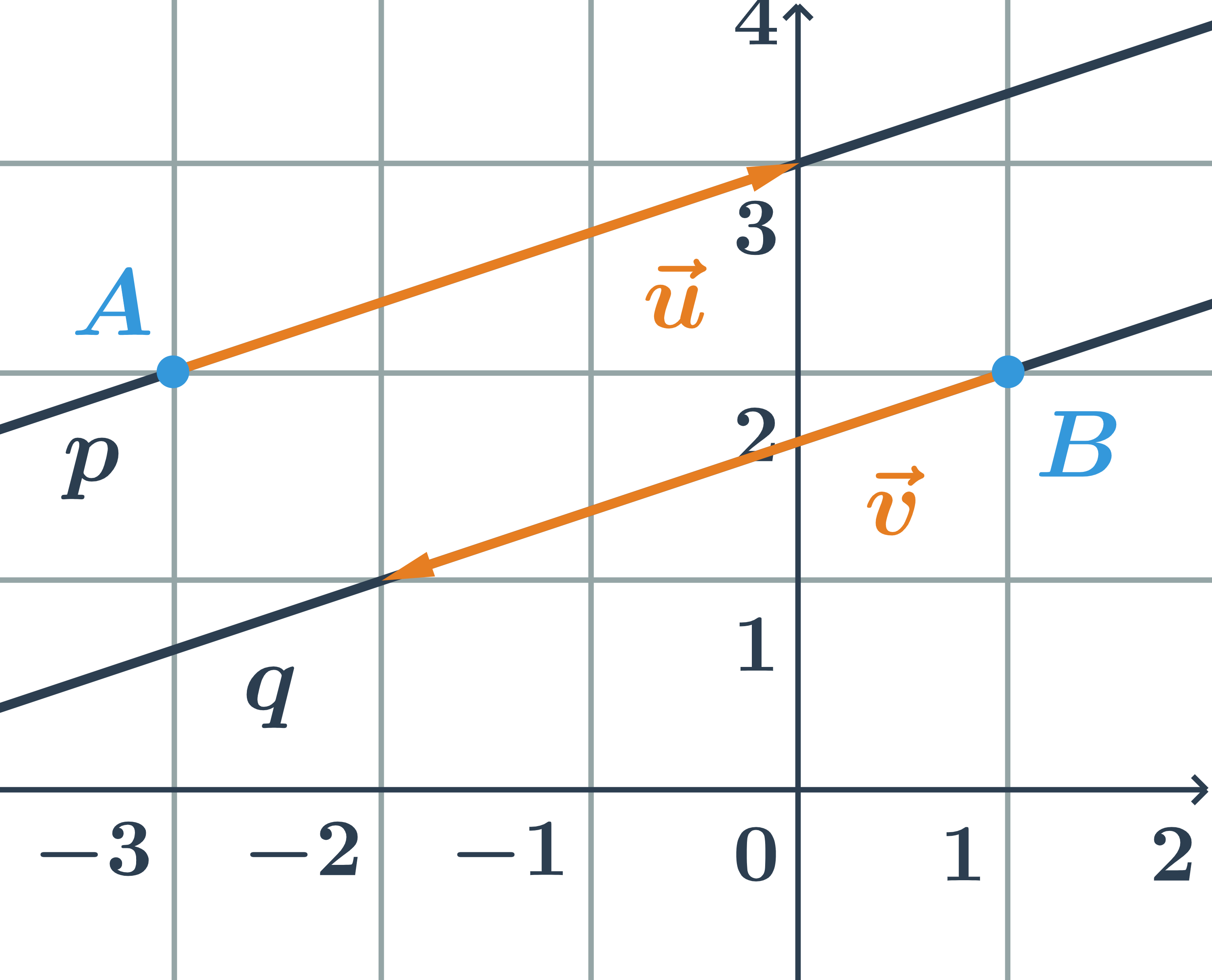
Rovnoběžky zadané obecnými rovnicemi
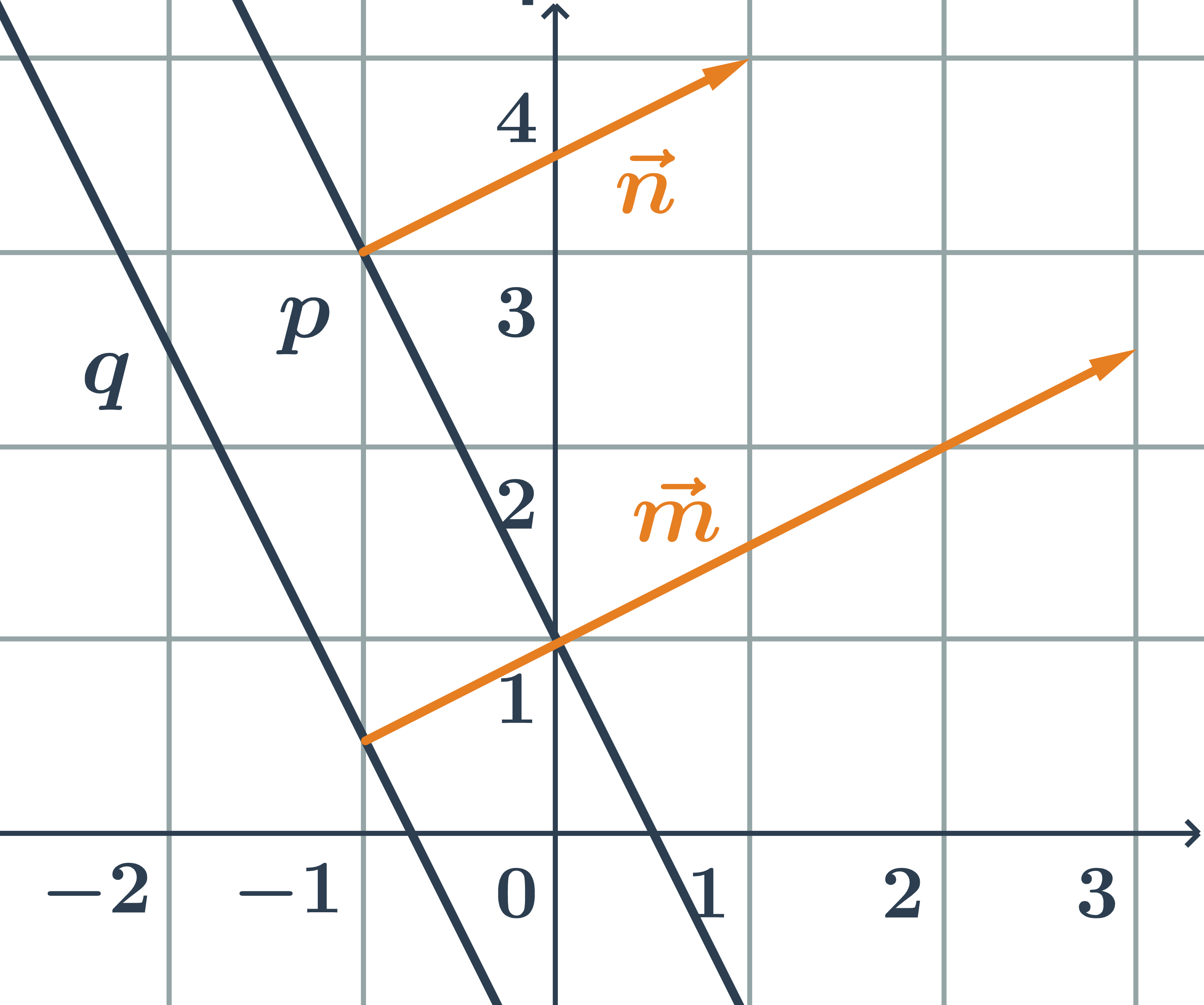
Určete vzájemnou polohu dvou přímek daných obecnými rovnicemi p: 2x+y-1=0 a q:4x+2y+3=0.
- normálový vektor přímky p:\hspace{0.25cm}\vec{n}=(2;1)
- normálový vektor přímky q:\hspace{0.25cm}\vec{m}=(4;2)
- Přímky p a q jsou rovnoběžné, protože jejich normálové vektory jsou kolineární.
- Ověříme, že přímky nejsou totožné. Stačí určit, zda bod, který leží na jedné přímce neleží na přímce druhé.
- Na přímce p leží například bod A=[0;1].
- Ověříme, zda A leží na p dosazením souřadnic bodu A do rovnice přímky p: 4\cdot0+2\cdot1+3\neq 0
- A nesplňuje rovnici, takže neleží na přímce q \Rightarrow přímky nejsou totožné
Různoběžky zadané parametrickými rovnicemi
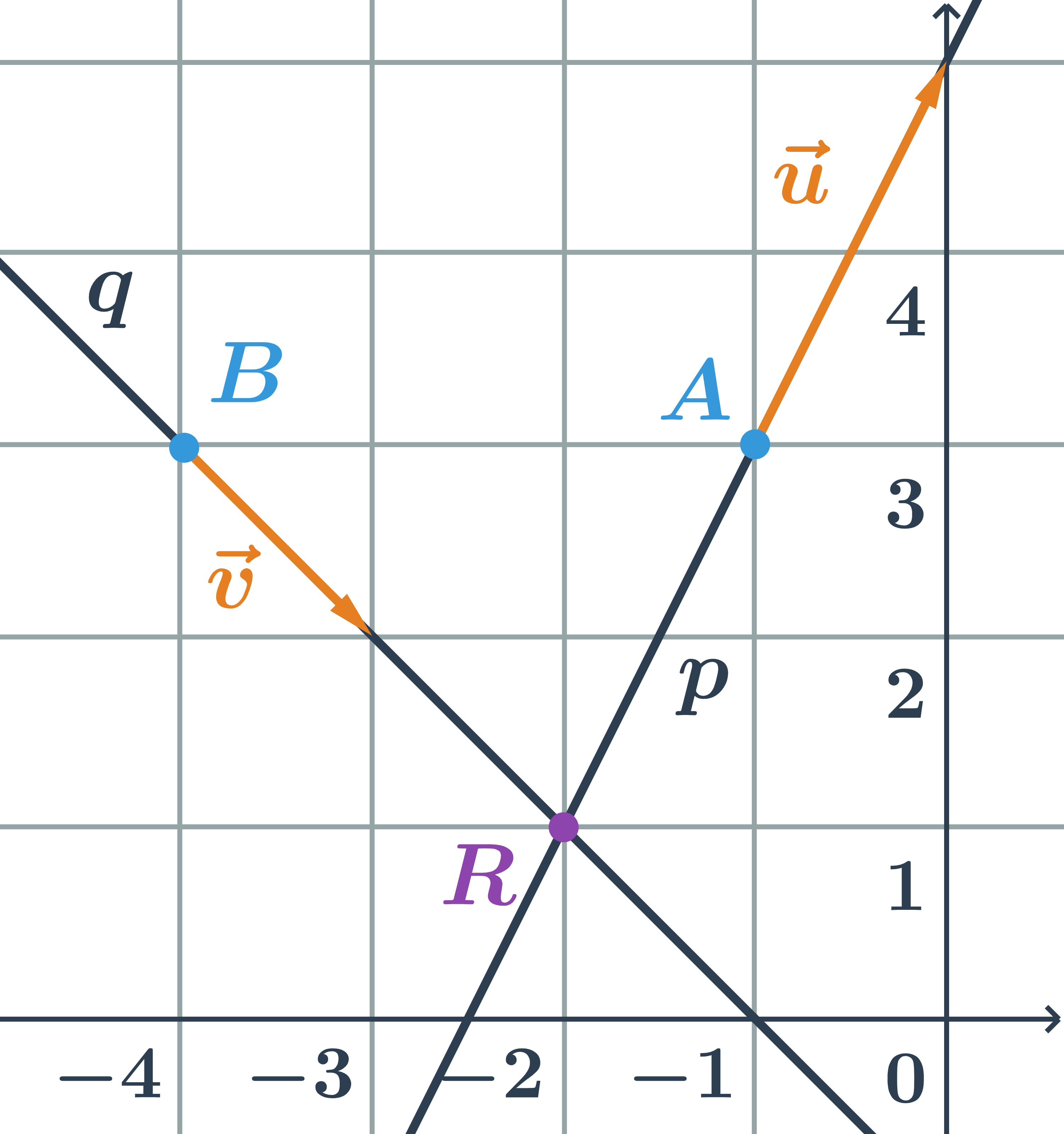
Určete vzájemnou polohu přímek p, q zadaných parametricky:
p: \begin{array}{rrl}x&=&-1+t\\y&=&\hspace{0.25cm}3+2t\\&&\hspace{0.25cm}t\in\mathbb{R}\end{array} \hspace{0.5cm}q: \begin{array}{rrl}x&=&-4+s\\y&=&\hspace{0.25cm}3-s\\&&\hspace{0.25cm}s\in\mathbb{R}\end{array}
- směrový vektor přímky p:\hspace{0.25cm}\vec{u}=(1;2)
- směrový vektor přímky q:\hspace{0.25cm}\vec{v}=(1;-1)
- Přímky p a q jsou různoběžné, protože jejich směrové vektory nejsou kolineární.
Průsečík přímek splňuje rovnice obou přímek, tedy každou z jeho souřadnic lze vyjádřit dvěma způsoby, dostáváme následující soustavu rovnic: \begin{array}{lrr}-1+t&=&-4+s\\\hspace{0.25cm}3+2t&=&3-s\end{array}
- Soustavu můžeme vyřešit sečtením obou rovnic: 2+3t=-1\Rightarrow3+3t=0\Rightarrow t=-1
- Výsledný parametr t dosadíme do parametrických rovnic kterékoliv z přímek a dostaneme souřadnice x,y průsečíku.
Průsečík přímek p a q je bod R=[-2;1].
Různoběžky zadané obecnými rovnicemi
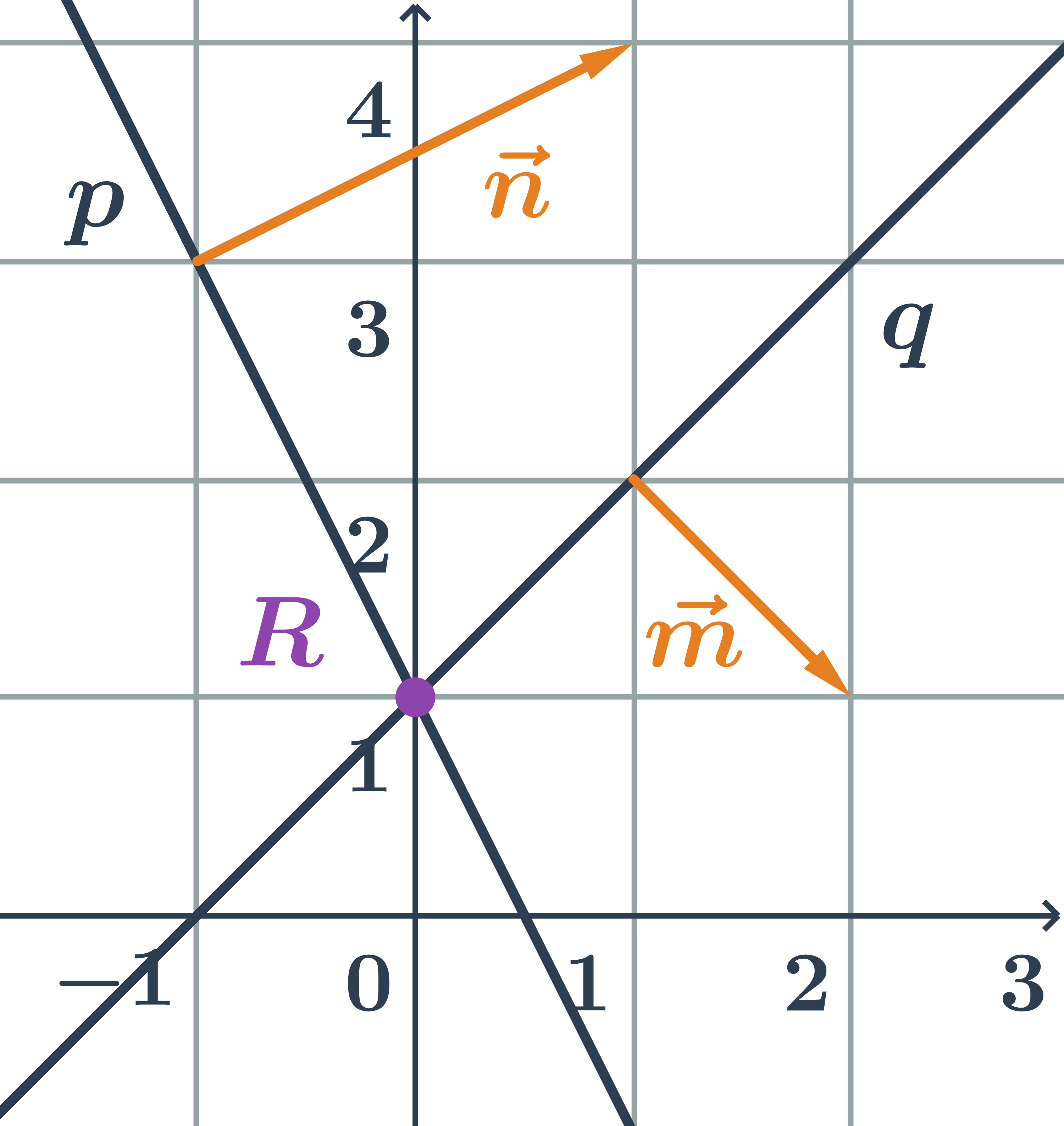
Určíme vzájemnou polohu dvou přímek zadaných obecnými rovnicemi p: 2x+y-1=0 a q:x-y+1=0.
- normálový vektor přímky p:\hspace{0.25cm}\vec{n}=(2;1)
- normálový vektor přímky q:\hspace{0.25cm}\vec{m}=(1;-1)
- Přímky p a q jsou různoběžné, protože jejich normálové vektory nejsou kolineární.
- Průsečík přímek splňuje rovnice obou přímek, tedy jeho souřadnice jsou řešením soustavy: \begin{array}{rrr}2x+y-1&=&0\\x-y+1&=&0\end{array}
- Můžeme vyřešit sečtením obou rovnic: 3x=0\Rightarrow x=0
- Průsečík přímek p a q je bod R=[0;1]
Přímka daná obecnou rovnicí a druhá parametricky – první příklad
Určete vzájemnou polohu přímek p,q zadaných takto:
\hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} \hspace{0.5cm}q: \begin{array}{rrl}x&=&3-2t\\y&=&2-4t\\&&t\in\mathbb{R}\end{array}
- normálový vektor přímky p:\hspace{0.25cm}\vec{n}=(2;-1)
- směrový vektor přímky q:\hspace{0.25cm}\vec{v}=(-2;-4)
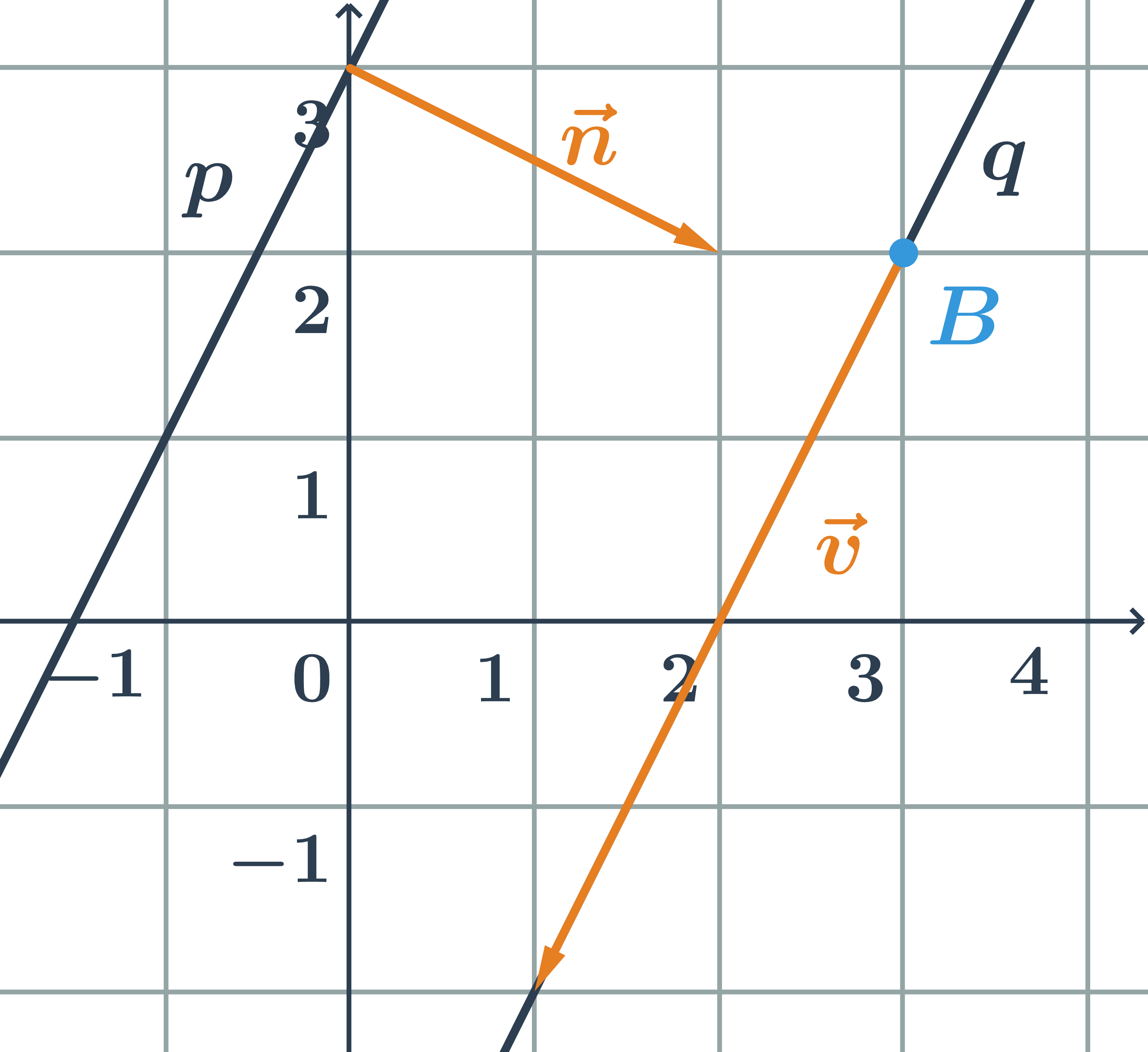
- Přímky p a q jsou rovnoběžné, protože jejich směrové vektory jsou kolineární. Proto normálový vektor jedné přímky je kolmý ke směrovému vektoru druhé přímky.
- Ověříme, že přímky nejsou totožné: stačí určit, zda bod, který leží na jedné přímce neleží na přímce druhé.
- Na přímce q leží například bod B=[3;2].
- Na přímce p tento bod neleží, což zjistíme dosazením souřadnic bodu B do rovnice přímky: 2\cdot3-2+3\neq 0
- Bod B nesplňuje rovnici, takže neleží na přímce p \Rightarrow přímky nejsou totožné
Přímka daná obecnou rovnicí a druhá parametricky – druhý příklad
Určete vzájemnou polohu přímek p,q zadaných:
\hspace{0.25cm}p: x-3y+3=0\hspace{0.25cm} \hspace{0.5cm}q: \begin{array}{rrl}x&=&\hspace{0.28cm}1+t\\y&=&-2+2t\\&&\hspace{0.28cm}t\in\mathbb{R}\end{array}
- normálový vektor přímky p:\hspace{0.25cm}\vec{n}=(1;-3)
- směrový vektor přímky q:\hspace{0.25cm}\vec{v}=(1;2)
- Přímky p a q jsou různoběžné, protože jejich směrové vektory nejsou kolineární. Vyplývá z toho, že normálový vektor jedné přímky není kolmý ke směrovému vektoru druhé přímky.
- Průsečík přímek splňuje rovnice obou přímek, tedy jeho souřadnice najdeme tak, že parametrické vyjádření přímky q dosadíme do obecné rovnice přímky p: \begin{array}{rrl}(1+t)-3(-2+2t)+3&=&0\\1+t+6-6t+3&=&0\\10-5t&=&0\\t&=&2\end{array}
- Průsečík přímek p a q je bod R=[3;2]
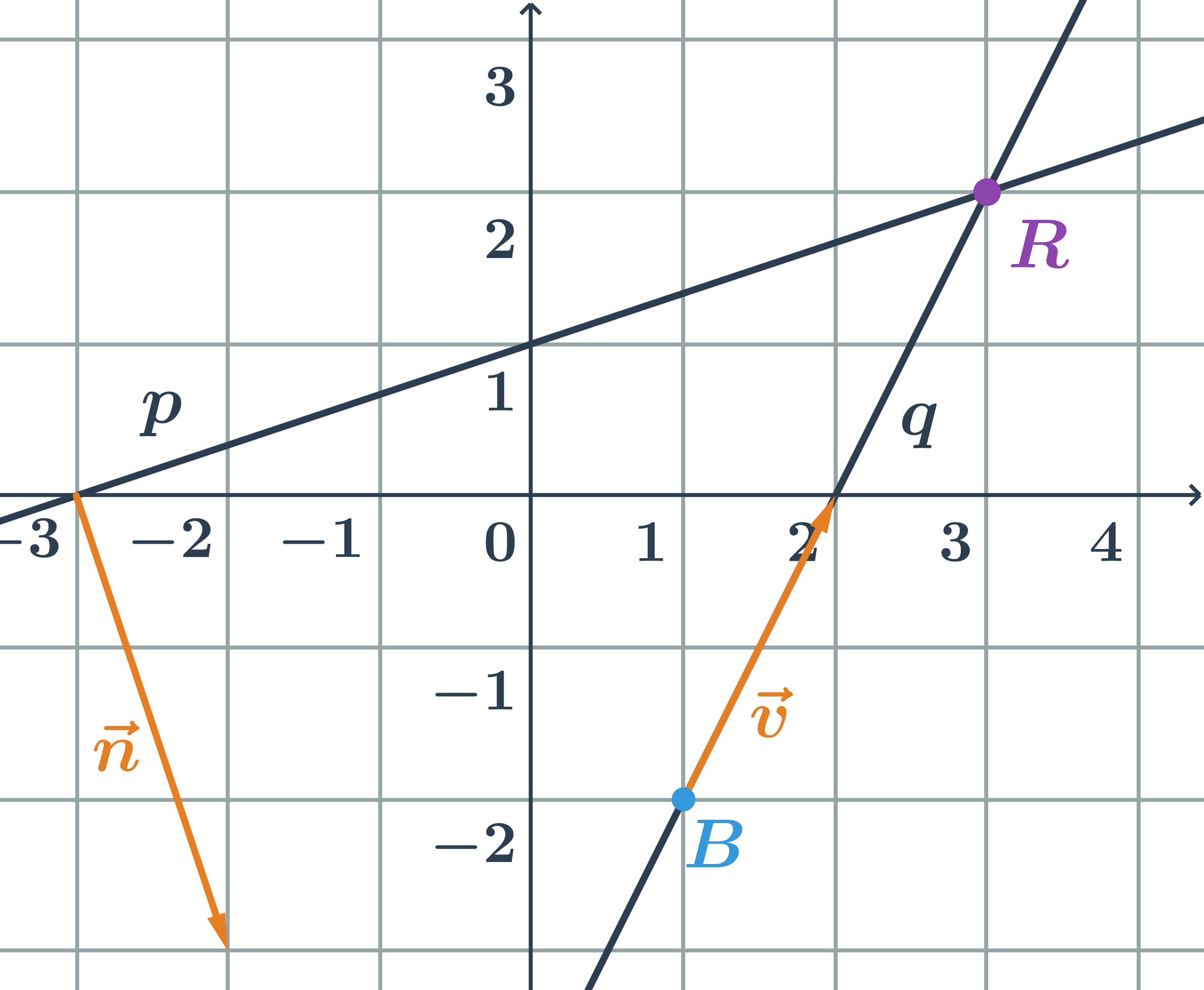
Souvislost počtu společných bodů přímek s počtem řešení soustavy rovnic
Pro určení společného bodu (bodů) dvou přímek, vždy řešíme soustavu rovnic. Tato soustava může mít:
- jedno řešení – přímky jsou různoběžné
- žádné řešení – přímky jsou rovnoběžné
- nekonečně mnoho řešení – přímky jsou totožné
Počet společných bodů – první příklad
Hledáme průsečík(y) přímek p,q zadaných jako: \hspace{0.25cm}p: x-3y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&\hspace{0.28cm}1+t\\y&=&-2+2t\end{array}
- Dosadíme parametrické vyjádření do obecné rovnice a řešíme soustavu rovnic:
\begin{array}{rrl}(1+t)-3(-2+2t)+3&=&0\\1+t+6-6t+3&=&0\\10-5t&=&0\\t&=&2\end{array}
- Jedno řešení \Rightarrow různoběžné přímky
Počet společných bodů – druhý příklad
Hledáme průsečík(y) přímek p,q zadaných jako: \hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&3-2t\\y&=&2-4t\end{array}
- Dosadíme parametrické vyjádření do obecné rovnice a řešíme soustavu rovnic:
\begin{array}{rrl}2(3-2t)-(2-4t)+3&=&0\\6-4t-2+4t+3&=&0\\7&=&0\end{array}
- Žádné řešení \Rightarrow různé rovnoběžné přímky
Počet společných bodů – třetí příklad
Hledáme průsečík(y) přímek p,q zadaných jako: \hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&3+t\\y&=&9+2t\end{array}
- Dosadíme parametrické vyjádření do obecné rovnice a řešíme soustavu rovnic:
\begin{array}{rrl}2(3+t)-(9+2t)+3&=&0\\6+2t-9-2t+3&=&0\\0&=&0\end{array}
- Nekonečně mnoho řešení \Rightarrow totožné přímky
Vzájemná poloha přímek v rovině (střední)

