
Konstrukce obecných čtyřúhelníků

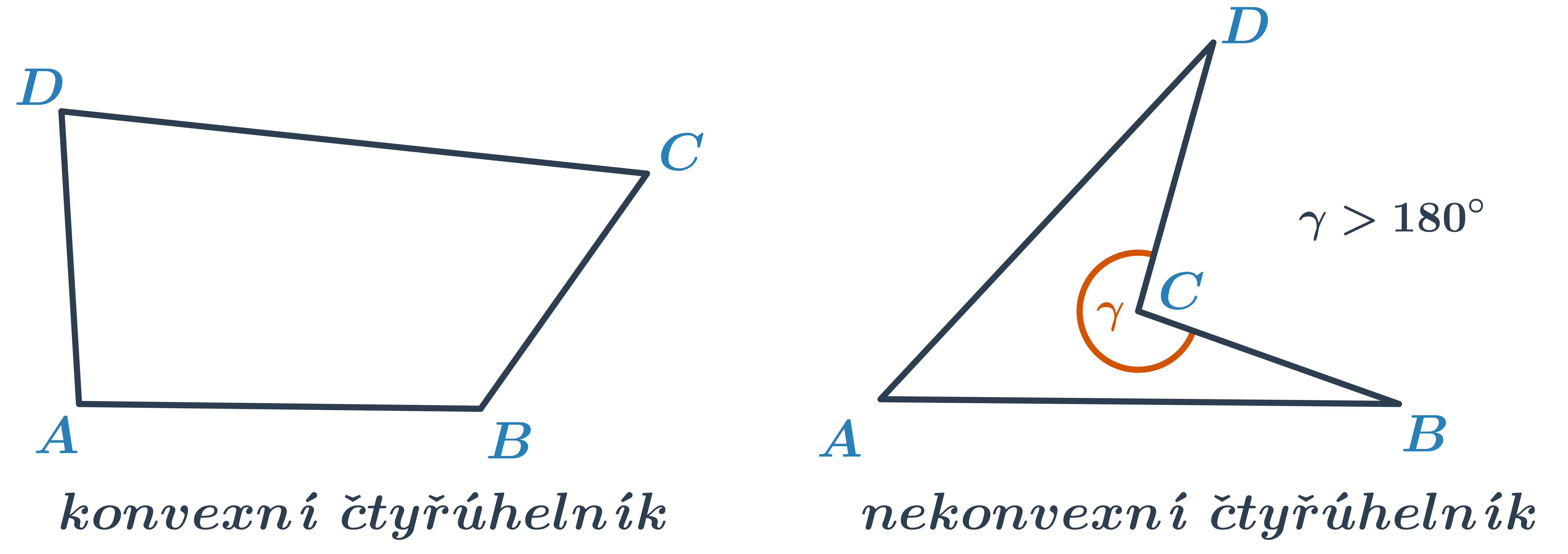
Víme, že čtyřúhelník je rovinný útvar ohraničený čtyřmi úsečkami, které spojují jeho vrcholy. Ve čtyřúhelníku může obecně být každá strana jinak dlouhá a každý vnitřní úhel může mít jinou velikost. Součet velikostí vnitřních úhlů je vždy 360^\circ. Pokud má čtyřúhelník všechny vnitřní úhly menší než 180^\circ, nazýváme ho konvexní. Speciálními případy konvexního čtyřúhelníku jsou čtverec, obdélník, rovnoběžník a lichoběžník. Pokud má čtyřúhelník jeden vnitřní úhel větší než 180^\circ, nazýváme ho nekonvexní.
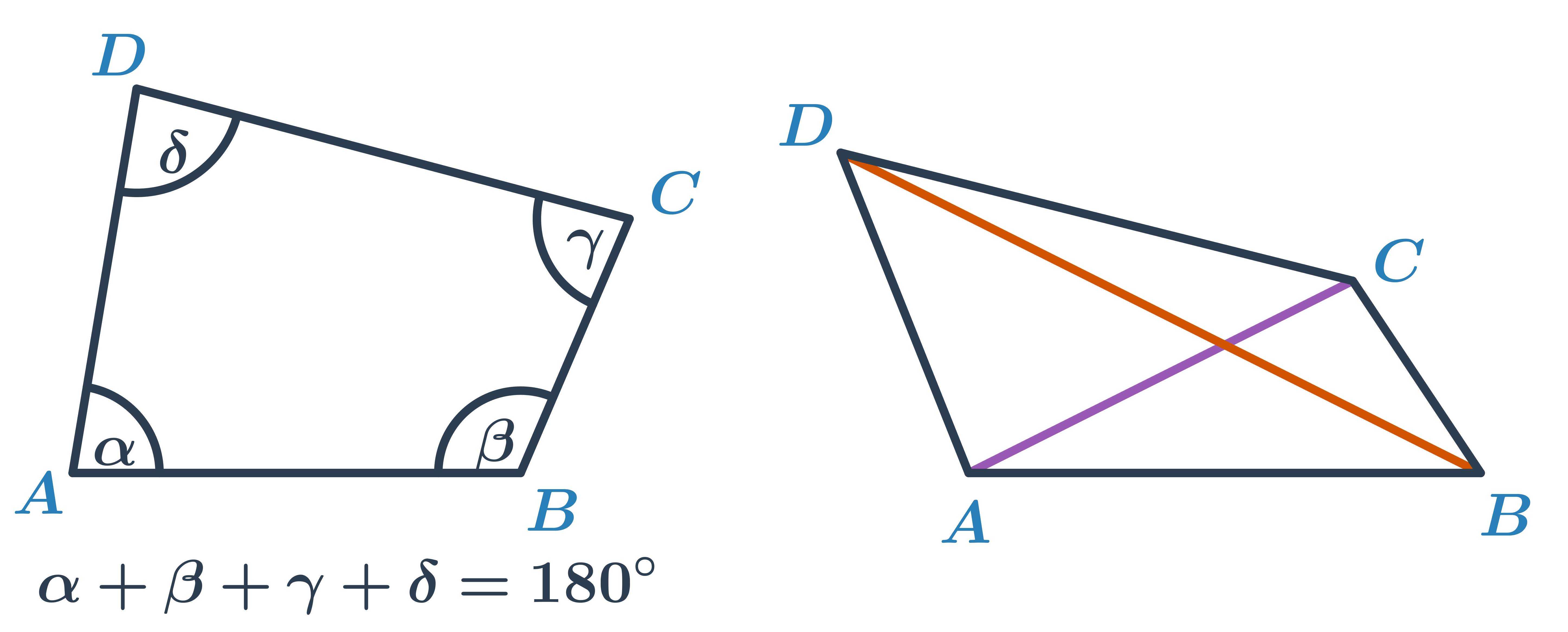
Úhlopříčky ve čtyřúhelníku mohou mít různou délku a rozdělují čtyřúhelník na dva trojúhelníky. Čtyřúhelník jako rovinný útvar si tak můžeme představit jako sjednocení dvou trojúhelníků. Toho často využijeme při konstrukci čtyřúhelníku, kdy jeden trojúhelník určený podle vět dokážeme sestrojit. Poslední vrchol pak doplníme pomocí zbývajících podmínek.
Příklad: konstrukce čtyřúhelníku, známé velikosti 3 stran a 2 úhlů
Sestrojte čtyřúhelník KLMN, je-li dáno |KL|=5 cm, |LM|=4 cm, |KN|=6 cm, |\sphericalangle NKL|=120^\circ,\ |\sphericalangle KLM|=100^\circ.
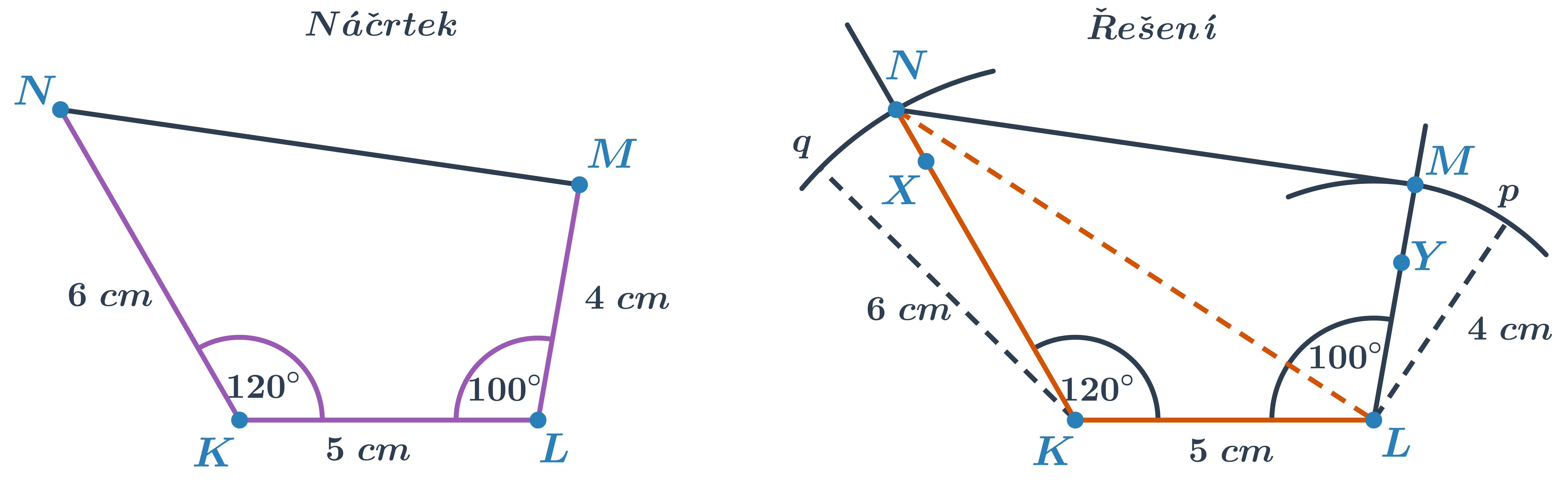
- Nejprve sestrojíme trojúhelník KLN určený podle věty sus.
- Dále sestrojíme úhel KLM pomocí polopřímky LY, která svírá s úsečkou KL úhel 100^\circ.
- Na polopřímku LY naneseme délku strany LM a dostaneme poslední vrchol M.
Kromě interaktivního procvičování níže je k dispozici ještě pracovní list k vytištění a rýsování na papíře:
Zavřít












