Čeština
Angličtina
Informatika
Biologie
Umíme to
Němčina
Zeměpis
Chemie
Dějepis
Fyzika
Aritmetika
Zlomky, procenta
Geometrie
Elementární algebra
Funkce
Jednotky, míry
Diskrétní matematika
Finanční gramotnost
Rozhodovačka
Pexeso
Krok po kroku
Psaná odpověď
Grafař
Porozumění
Přesouvání
Mřížkovaná
Rozdělovačka
Rozbitá kalkulačka
Roboti
Střílečka
Příšerky
Závody
Územíčka
Tipovačka
Týmovka
Metrické úlohy
V metrických úlohách v analytické geometrii bývá úkolem spočítat konkrétní číselnou hodnotu veličin jako je:
- vzdálenost dvou objektů, např. vzdálenost bodu od přímky,
- odchylka dvou přímek v rovině.
Vzdálenost bodu od přímky
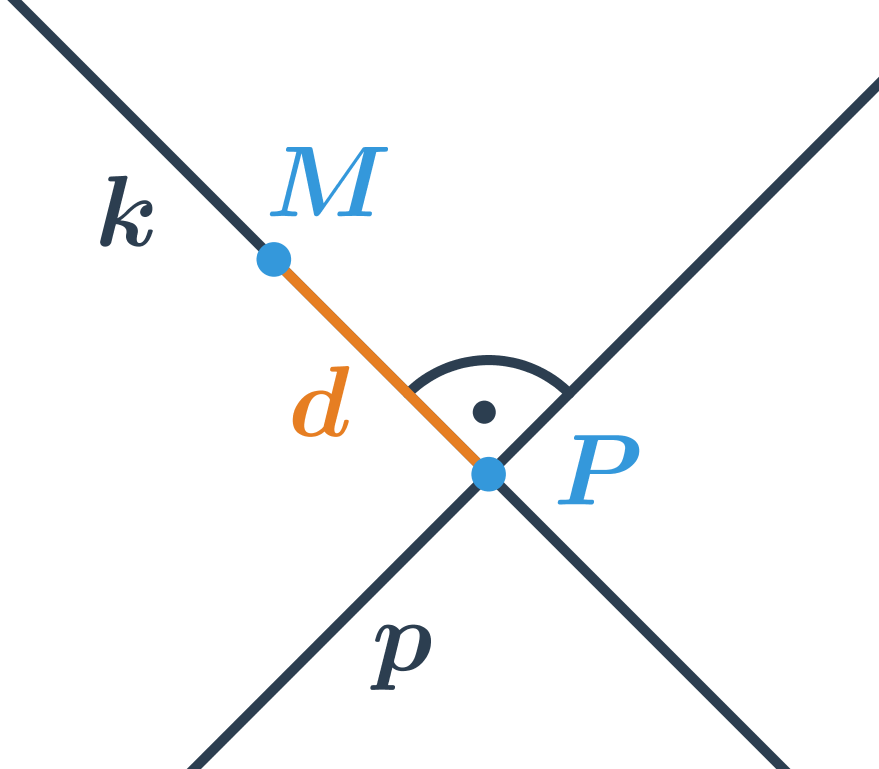
Vzdálenost bodu od přímky je délka nejkratší úsečky určené bodem M a bodem ležícím na přímce p. Jak je vidět z obrázku tato nejkratší úsečka leží na kolmici z bodu M k přímce p. Vzdálenost bodu od přímky tedy můžeme určit takto:
- najdeme přímku k, která prochází bodem M a je kolmá k přímce p
- určíme průsečík P přímky k s přímkou p
- vzdálenost bodu M od přímky p je délka úsečky PM
Příklad: vzdálenost bodu od přímky – pomocí kolmice
Určete vzdálenost bodu M=[5;2] od přímky p:4x+3y-1=0.
- Přímka k, která prochází bodem M a je kolmá k přímce p má směrový vektor kolineární s normálovým vektorem přímky p.
- Souřadnice směrového vektoru přímky k jsou: \vec{u}=(4;3).
- Přímka k má parametrické vyjádření: p:X=M+t\vec{u}
- p:\begin{array}{rrl}x&=&5+4t\\y&=&2+3t\\&&t\in\mathbb{R}\end{array}
- Souřadnice průsečíku P přímky k s přímkou p určíme dosazením parametrického vyjádření přímky k do obecné rovnice přímky p.
\begin{array}{rrl}4(5+4t)+3(2+3t)-1&=&0\\20+16t+6+9t-1&=&0\\25+25t&=&0\Rightarrow t=-1\end{array}
- Průsečík přímek k a p je bod P=[1;-1].
- Vzdálenost bodu M od přímky p je délka úsečky PM:
- Vzorec pro délku úsečky: d=\sqrt{(x_M-x_P)^2+(y_M-y_P)^2}
- Dosadíme souřadnice bodů M,P: d=\sqrt{(5-1)^2+(2-(-1))^2}=\sqrt{16+9}=5
Vzorec pro vzdálenost bodu od přímky dané obecnou rovnicí
Vzdálenost bodu M=[m_1;m_2] od přímky p dané obecnou rovnicí ax+by+c=0 je dána vzorcem: d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}}
Příklad: vzdálenost bodu od přímky – pomocí vzorce
Určete vzdálenost bodu M=[5;2] od přímky p:4x+3y-1=0 s využitím vzorce.
- Dosadíme do vzorce d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}} souřadnice bodu M=[5;2] a koeficienty a a b z obecné rovnice přímky.
- Obecná rovnice pro p je 4x+3y-1=0, tedy a=4 a b=3.
- Máme: d=\frac{\left| 4\cdot5+3\cdot2-1\right|}{\sqrt{4^2+3^2}}=\frac{25}{\sqrt{25}}=5
Vzdálenost dvou rovnoběžek
Umíme-li určit vzdálenost bodu od přímky, snadno určíme také vzdálenost dvou rovnoběžek. Stačí si uvědomit, že všechny body ležící na jedné přímce mají od druhé přímky stejnou vzdálenost. Proto je vzdálenost rovnoběžek stejná jako vzdálenost libovolného bodu na jedné přímce od přímky druhé.
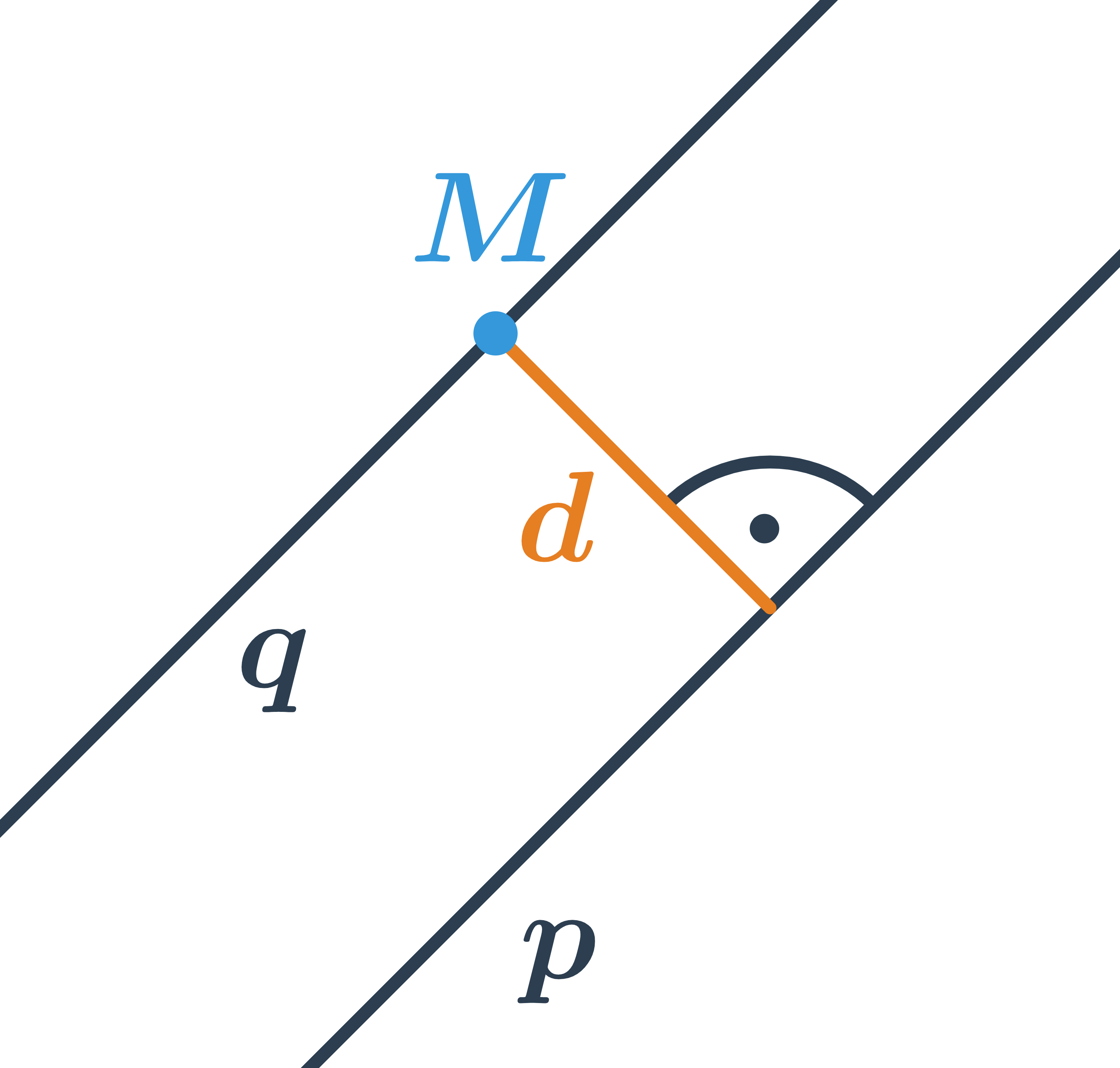
Příklad: vzdálenost rovnoběžek
Určete vzdálenost rovnoběžek p:2x-4y+3=0 a q:x-2y+1=0.
- Určíme souřadnice jednoho bodu (M) na přímce q tak, že jednu souřadnici zvolíme a druhou dopočítáme.
- Zvolíme například souřadnici y=0, pak x-2\cdot0+1=0\Rightarrow x=-1
- Dosadíme do vzorce d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}} souřadnice bodu M=[-1;0] a koeficienty a a b z obecné rovnice přímky p.
- Obecná rovnice pro p je 2x-4y+3=0, tedy a=2 a b=-4.
- Máme: d=\frac{\left| 2\cdot(-1)-4\cdot0+3\right|}{\sqrt{2^2+(-4)^2}}=\frac{1}{\sqrt{20}}
- Vzdálenost rovnoběžek p a q je: d=\frac{1}{\sqrt{20}}
Odchylka dvou přímek
Odchylka rovnoběžek je 0^\circ. Odchylka různoběžek je velikost ostrého nebo pravého úhlu, který přímky svírají.
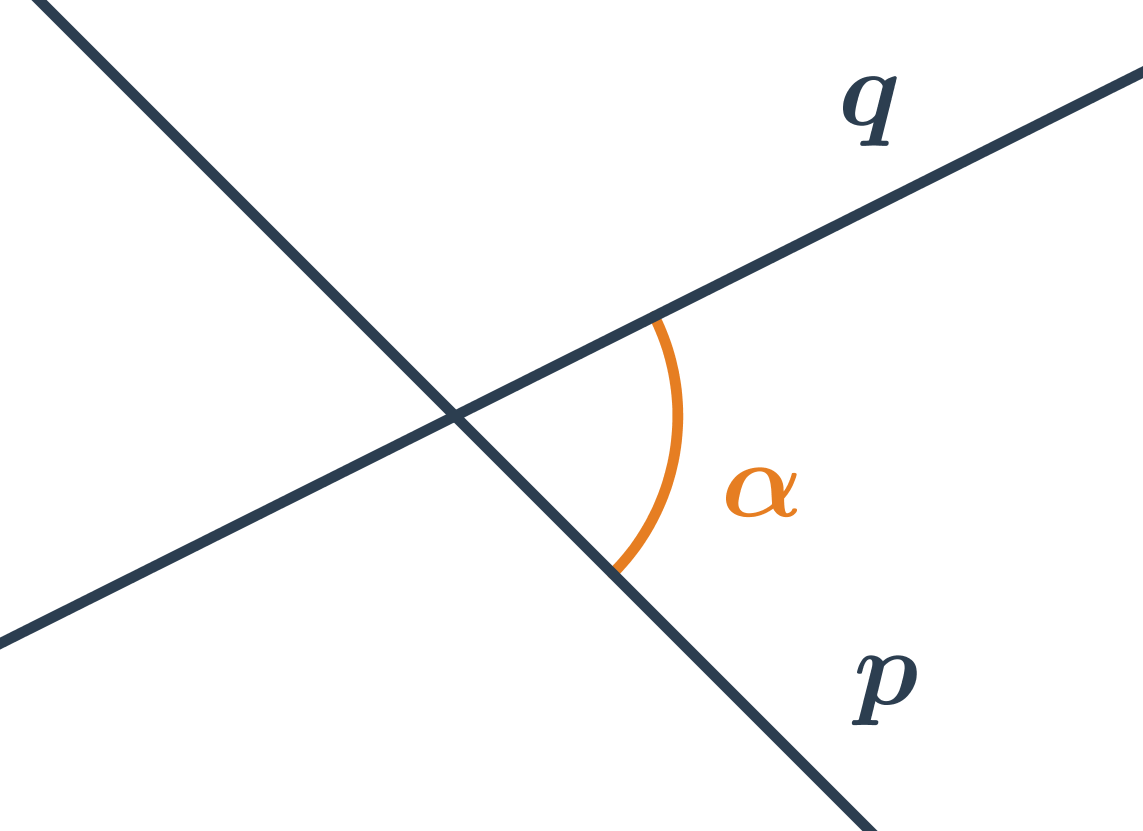
Odchylku různoběžek p a q můžeme vypočítat na základě znalosti směrových nebo normálových vektorů přímek. Vzorec pro výpočet úhlu různoběžek je obdobný jako vzorec pro výpočet úhlu vektorů
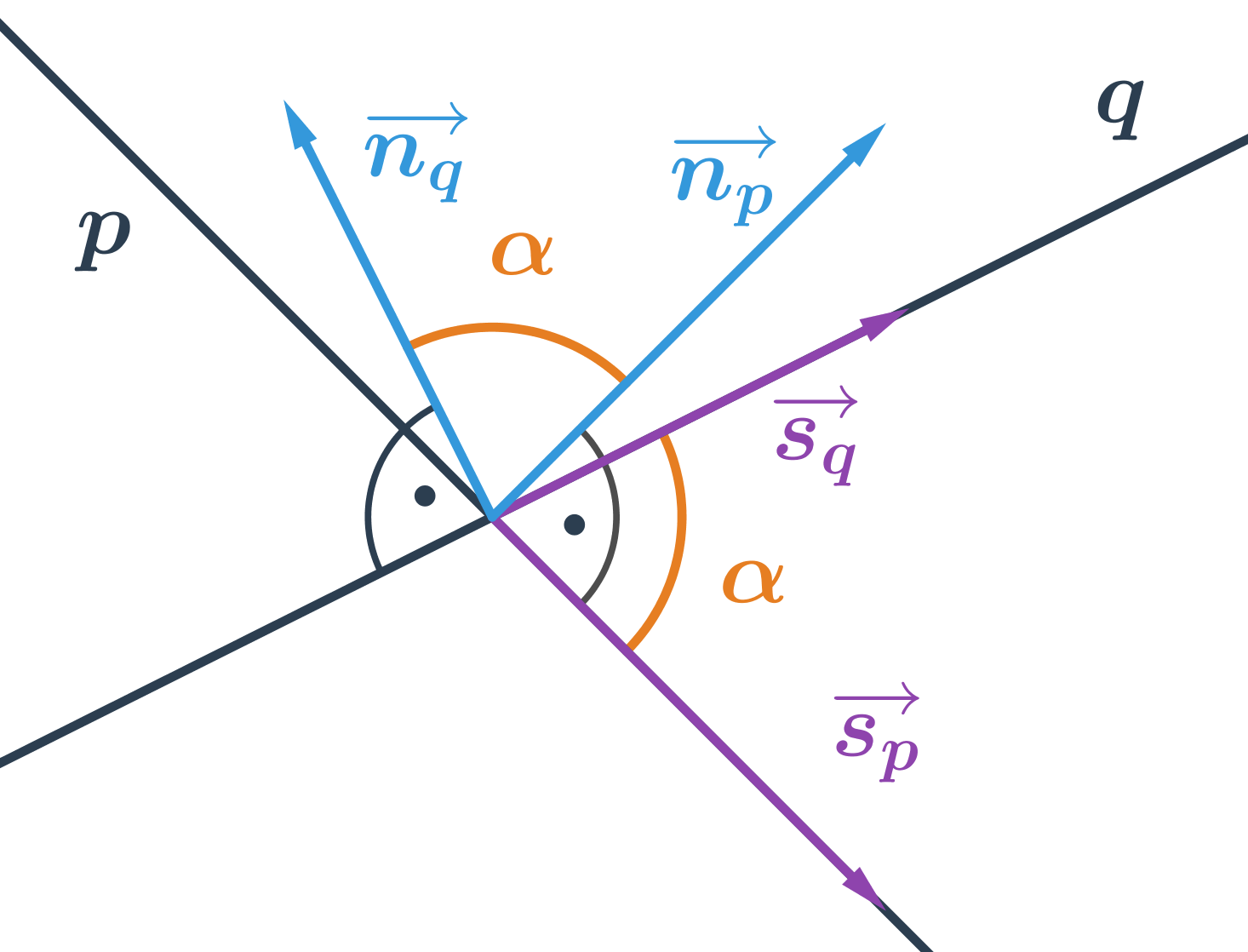
Odchylka různoběžek je úhel \alpha, pro který platí: \cos \alpha =\frac{\left| \vec{u} \cdot \vec{v} \right|}{\left| \vec{u} \right|\cdot \left| \vec{v} \right|} Vektory \vec{u} a \vec{v} uvedené ve vzorci jsou směrové vektory \overrightarrow{s_p} a \overrightarrow{s_q} nebo normálové vektory \overrightarrow{n_p} a \overrightarrow{n_q} přímek p a q.
Pro dvě k sobě kolmé přímky platí, že jejich odchylka \alpha=90^\circ a tedy \cos\alpha=0.
Proč musí být ve vzorci pro výpočet odchylky přímek absolutní hodnota?
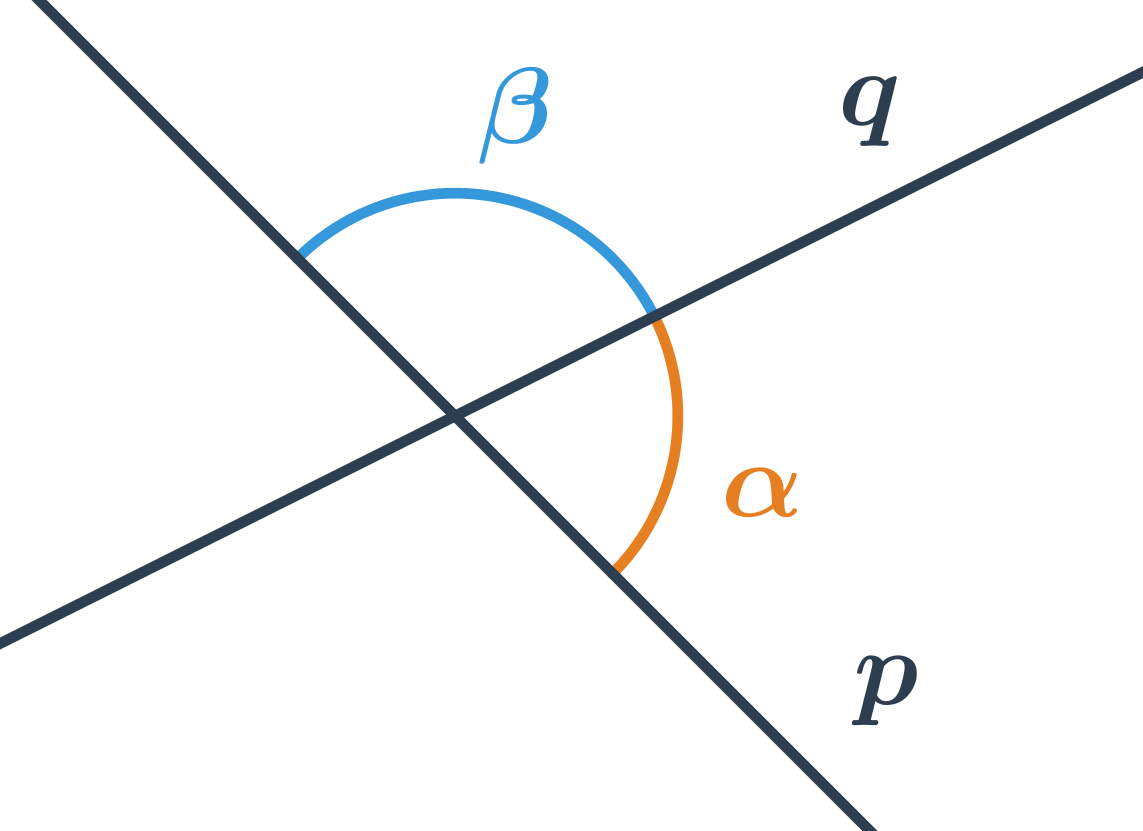
- Odchylka přímek p a q na obrázku je ostrý úhel \alpha, nikoliv tupý úhel \beta.
- \alpha a \beta jsou vedlejší úhly, pro které je hodnota funkce \cos opačná, tedy: \cos\alpha=-\cos\beta
- Pro úhel \alpha je \cos\alpha>0, pro \beta je \cos\beta<0
- Absolutní hodnota ve vzorci nám zaručí, že najdeme úhel, kde hodnota funkce \cos je kladná, tedy úhel ostrý, který je odchylkou daných přímek.
Odchylka přímek a úhly v trojúhelníku
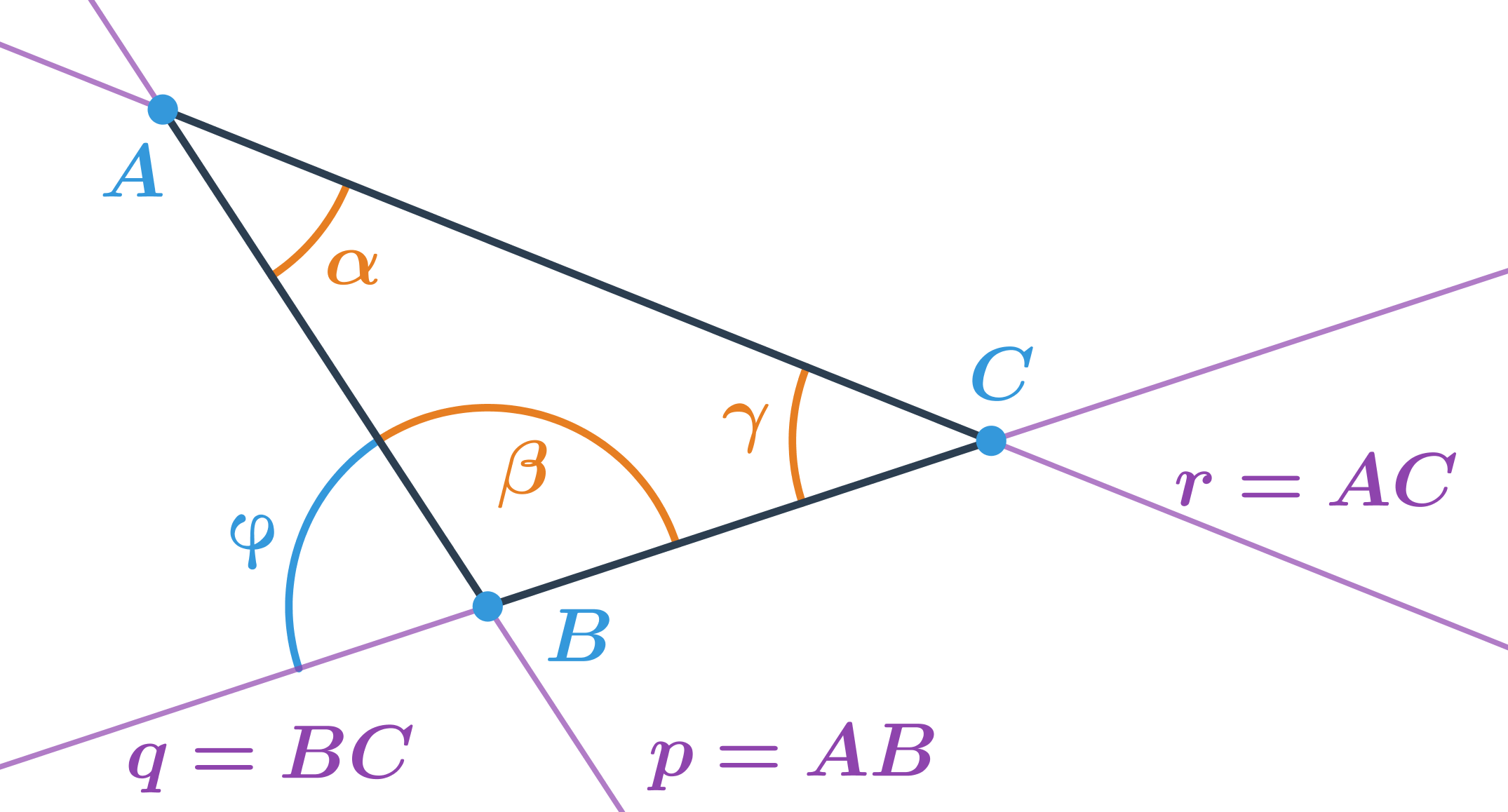
V trojúhelníku na obrázku:
- úhel \alpha je menší než 90^\circ a je to odchylka přímek AB a AC
- úhel \beta je větší než 90^\circ a není to odchylka přímek AB a BC
- úhel \gamma je menší než 90^\circ a je to odchylka přímek BC a AC
Velikost úhlů v trojúhelníku nemusí být stejná jako odchylka přímek, na kterých leží strany trojúhelníku. Úhly v trojúhelníku počítáme jako odchylku vektorů, které určují daný úhel. Tento úhel může být větší než 90^\circ, proto využijeme vzorec pro výpočet odchylky vektorů (ve vzorci nebude absolutní hodnota).
Odchylka přímek
Určete odchylku přímek p:x-2y+3=0 a q:2x-y+1=0
- Přímky jsou dané obecnými rovnicemi, proto pro výpočet jejich odchylky využijeme normálové vektory: \overrightarrow{n_p}=(1;-2) a \overrightarrow{n_q}=(2;-1)
- Dosadíme do vzorce: \cos \alpha =\frac{\left| \vec{u} \cdot \vec{v} \right|}{\left| \vec{u} \right|\cdot \left| \vec{v} \right|}=\frac{\left| 1\cdot2+(-2) \cdot(-1) \right|}{\sqrt{1^2+(-2)^2}\cdot\sqrt{2^2+(-1)^2}}=\frac{4}{\sqrt{5}\cdot \sqrt{5}}=\frac{4}{5}
- Pomocí funkce cos^{-1} na kalkulačce dopočítáme odchylku: \alpha=36^\circ
